人教版(2019)选择性必修一 2.1 简谐运动 课件25张
文档属性
| 名称 | 人教版(2019)选择性必修一 2.1 简谐运动 课件25张 |  | |
| 格式 | pptx | ||
| 文件大小 | 12.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-16 18:28:04 | ||
图片预览





文档简介
(共25张PPT)
机械振动
第1节 简谐运动
一、观察生活
钟摆来回摆动,水中浮标上下浮动,担物行走时扁担下物体的颤动,树梢在微风中的摇摆……这些运动的共同点是什么?
左右往复运动
前后往复运动
上下往复运动
上述物体总是在某一位置
附近做往复性的运动。
摇曳的树梢
现象总结
简称:振动。
一、机械振动
均在围绕某一位置,做往复运动。
物体或物体的一部分在一个位置附近的往复运动。
机械振动:
你能举出生活中,机械振动的其他例子吗?
蜜蜂的翅膀
吉他的弦
敲打后的鼓面
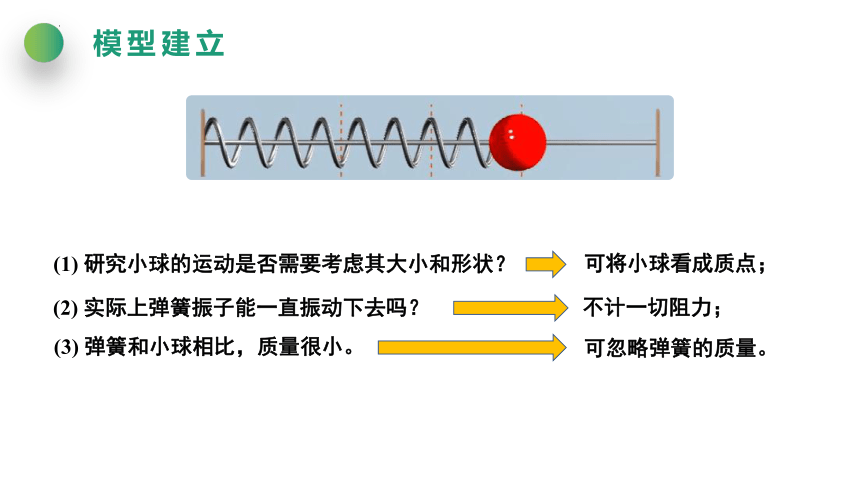
可将小球看成质点;
不计一切阻力;
可忽略弹簧的质量。
(1) 研究小球的运动是否需要考虑其大小和形状?
(2) 实际上弹簧振子能一直振动下去吗?
(3) 弹簧和小球相比,质量很小。
模型建立
模型建立
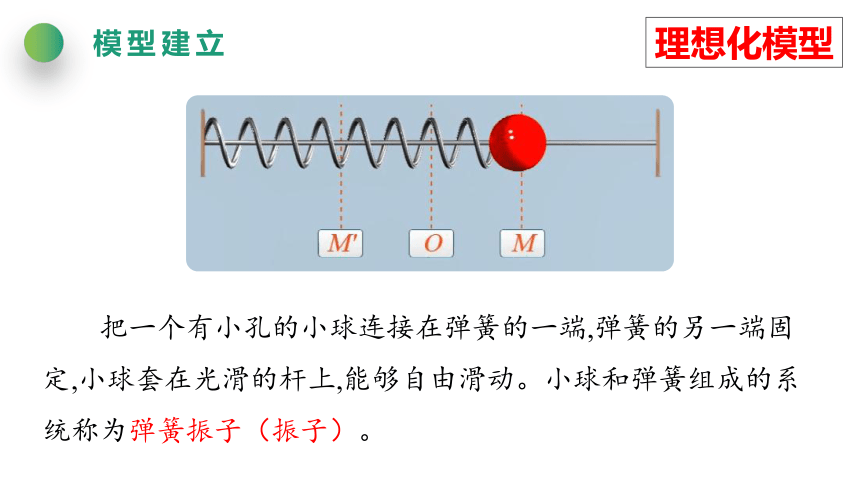
理想化模型
把一个有小孔的小球连接在弹簧的一端,弹簧的另一端固定,小球套在光滑的杆上,能够自由滑动。小球和弹簧组成的系统称为弹簧振子(振子)。
再观察振子的运动
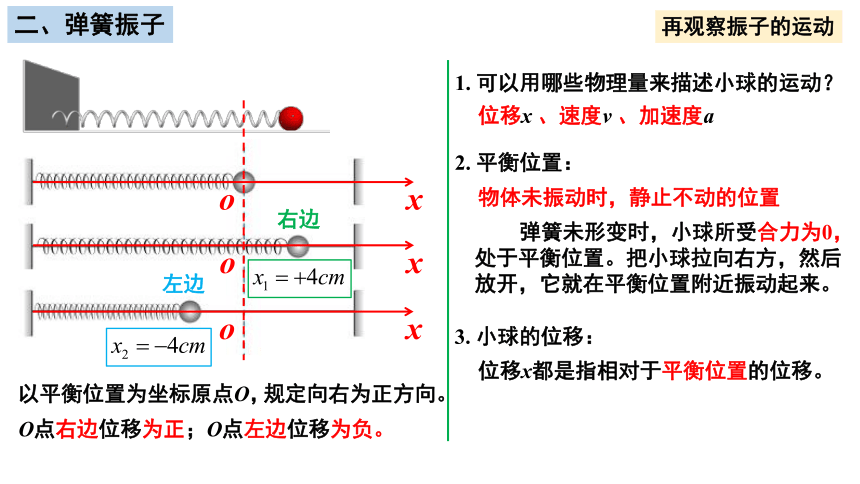
1. 可以用哪些物理量来描述小球的运动?
位移x 、速度v 、加速度a
物体未振动时,静止不动的位置
2. 平衡位置:
二、弹簧振子
o
x
以平衡位置为坐标原点O,
规定向右为正方向。
o
x
o
x
3. 小球的位移:
位移x都是指相对于平衡位置的位移。
O点右边位移为正;O点左边位移为负。
右边
左边
弹簧未形变时,小球所受合力为0,处于平衡位置。把小球拉向右方,然后放开,它就在平衡位置附近振动起来。
再观察振子的运动
二、弹簧振子
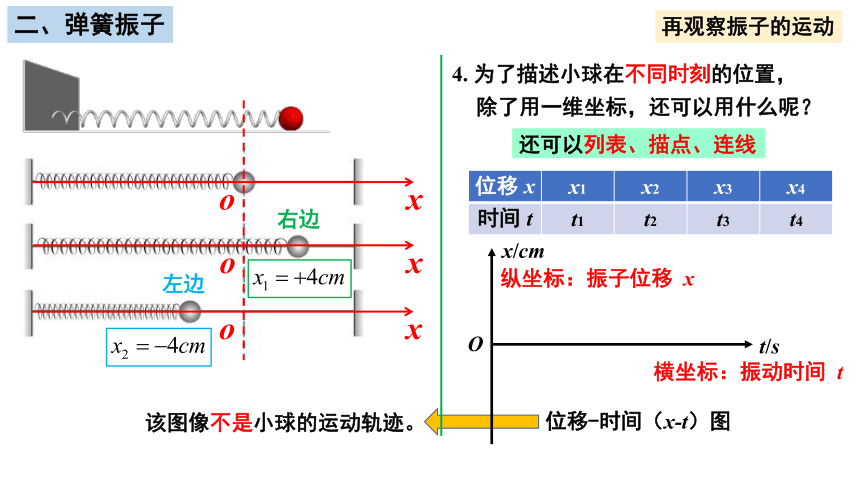
横坐标:振动时间 t
纵坐标:振子位移 x
O
位移-时间(x-t)图
4. 为了描述小球在不同时刻的位置,
除了用一维坐标,还可以用什么呢?
o
x
o
x
o
x
位移 x x1 x2 x3 x4
时间 t t1 t2 t3 t4
x/cm
t/s
还可以列表、描点、连线
该图像不是小球的运动轨迹。
右边
左边
(1)请你拿起手中的笔,在白纸上方模拟水平弹簧振子在平衡位置附近左右往复运动,你会得到怎样的图像?
方法一:手动描图法
5. 怎么描绘振子的位移-时间( x-t )图像呢?
(2)一位同学匀速拉动白纸,另一同学沿与纸运动方向相垂直方向用笔往复画线段,你会得到怎样的图像?
再观察振子的运动
二、弹簧振子
记录数据
(以向右为正方向)
5. 怎么描绘振子的位移-时间( x-t )图像呢?
方法三:频闪照相法
二、弹簧振子
再观察振子的运动
t/s
x/mm
20
-20
10
-10
3t0
6t0
9t0
12t0
15t0
O
5. 怎么描绘振子的位移-时间( x-t )图像呢?
方法三:频闪照相法
二、弹簧振子
再观察振子的运动
列表、描点、连线
6. 怎么证明x - t图像是“正弦式”函数图像?
再观察振子的运动
二、弹簧振子
选取小球平衡位置为坐标原点,建立坐标系,横轴和纵轴分别表示时间t和小球的位移x。在坐标系中标出各时刻小球球心的位置,用曲线把各点连接起来,就是小球在平衡位置附近往复运动时的位移—时间图像,即x-t图像。x-t图像即振动图像。
从弹簧振子的x-t图像可以看出,小球位移与时间的关系似乎可以用正弦函数来表示。
6. 怎么证明x - t图像是“正弦式”函数图像?
再观察振子的运动
二、弹簧振子
方法一:利用数学函数表达式
假定图中的曲线是正弦曲线,测量它的振幅和周期,写出对应的正弦函数的表达式。
上图中,测量小球在各个位置的横坐标和纵坐标。把测量值输入计算机中,作出这条曲线,看一看小球的位移—时间关系是否可以用正弦函数表示。通过仔细分析会发现,小球位移与时间的关系是正弦函数关系。
方法二:利用计算机数值拟合
结论:水平弹簧振子的x-t图像是正弦函数图像。
如果质点的位移与时间的关系遵从正弦函数的规律,即它的振动图象(x-t 图象)是一条正弦曲线,
简谐运动是生活中最基本、最简单的振动,
这样的振动被称为简谐运动(simple harmonic motion)。
简谐运动:
例:水平弹簧振子
三、简谐运动
生活中的复杂振动都可以看成是很多简谐运动的合成。
B
C
由简谐运动的图像获取的信息
三、简谐运动
C
B
O
小球在BC之间来回运动,O为平衡位置。
B:正方向最大位移,速度为零,弹力最大;
C:负方向最大位移,速度为零,弹力最大;
位移 速度 弹簧弹力 加速度
B 负方向最大 零 最大 最大
O 零 最大 零 零
C 正方向最大 零 最大 最大
规定向右为正方向
过程 加速度大小变化 速度大小变化
A到O
O到B
B到O
O到B
衡位置时
远离平衡位置时
由简谐运动的图像获取的信息
三、简谐运动
B
C
C
B
O
规定向右为正方向
由简谐运动的图像获取的信息
三、简谐运动
(1)某一时刻质点的位移大小和方向:
质点在t1、t2时刻的位移分别为x1和-x2.
小球在BC之间来回运动,O为平衡位置。
B
C
C
B
O
规定向右为正方向
由简谐运动的图像获取的信息
三、简谐运动
如图中a点,下一时刻质点离平衡位置更远,故a点对应时刻质点向正方向远离平衡位置运动。
B
C
C
B
O
规定向右为正方向
(2)某一时刻质点的运动(速度)方向:
小球在BC之间来回运动,O为平衡位置。
由简谐运动的图像获取的信息
三、简谐运动
①观察下一时刻质点的位移:
(3)质点的速度、位移的变化情况:
小球在BC之间来回运动,O为平衡位置。
B
C
C
B
O
规定向右为正方向
若下一时刻远离平衡位置,则速度越来越小,位移越来越大;若衡位置,则速度越来越大,位移越来越小.
由简谐运动的图像获取的信息
三、简谐运动
②根据斜率判断速度的大小和方向:
斜率:
B
C
C
B
O
规定向右为正方向
(3)质点的速度、位移的变化情况:
小球在BC之间来回运动,O为平衡位置。
斜率越大,则速度越大,斜率越小,则速度越小;斜率为正,则速度沿正方向,斜率为负,则速度沿负方向.
四、复杂振动
心电图
x
t
四、复杂振动
例1. 如图是某质点做简谐运动的振动图像。根据图像中的信息,回答下列问题。
(1)质点离开平衡位置的最大距离有多大?
(2)在1.5s和2.5s这两个时刻,质点的位置在哪里?质点向哪个方向运动?
五、练习与应用
例1. 如图是某质点做简谐运动的振动图像。根据图像中的信息,回答下列问题。
(3)质点相对于平衡位置的位移方向在哪些时间内跟它的瞬时速度的方向相同?在哪些时间内跟瞬时速度的方向相反?
(4)质点在第2s末的位移是多少?
(5)质点在前2s内运动的路程是多少?
四、练习与应用
三、简谐运动
新课讲授
方法一:正弦函数代入法
(1)假定所得曲线是正弦曲线,测量它的振幅和周期,写出对应的正弦函数表达式;
(2)在图中选小球若干个位置,用刻度尺在图中测量增坐标,将每个位移对应的振动时间代入表达式求出函数值,比较这一函数值与测量值,看是否相等,若可视为相等,则这条曲线就是正弦曲线。
三、简谐运动
新课讲授
方法二:计算机函数图像耦合法
机械振动
第1节 简谐运动
一、观察生活
钟摆来回摆动,水中浮标上下浮动,担物行走时扁担下物体的颤动,树梢在微风中的摇摆……这些运动的共同点是什么?
左右往复运动
前后往复运动
上下往复运动
上述物体总是在某一位置
附近做往复性的运动。
摇曳的树梢
现象总结
简称:振动。
一、机械振动
均在围绕某一位置,做往复运动。
物体或物体的一部分在一个位置附近的往复运动。
机械振动:
你能举出生活中,机械振动的其他例子吗?
蜜蜂的翅膀
吉他的弦
敲打后的鼓面
可将小球看成质点;
不计一切阻力;
可忽略弹簧的质量。
(1) 研究小球的运动是否需要考虑其大小和形状?
(2) 实际上弹簧振子能一直振动下去吗?
(3) 弹簧和小球相比,质量很小。
模型建立
模型建立
理想化模型
把一个有小孔的小球连接在弹簧的一端,弹簧的另一端固定,小球套在光滑的杆上,能够自由滑动。小球和弹簧组成的系统称为弹簧振子(振子)。
再观察振子的运动
1. 可以用哪些物理量来描述小球的运动?
位移x 、速度v 、加速度a
物体未振动时,静止不动的位置
2. 平衡位置:
二、弹簧振子
o
x
以平衡位置为坐标原点O,
规定向右为正方向。
o
x
o
x
3. 小球的位移:
位移x都是指相对于平衡位置的位移。
O点右边位移为正;O点左边位移为负。
右边
左边
弹簧未形变时,小球所受合力为0,处于平衡位置。把小球拉向右方,然后放开,它就在平衡位置附近振动起来。
再观察振子的运动
二、弹簧振子
横坐标:振动时间 t
纵坐标:振子位移 x
O
位移-时间(x-t)图
4. 为了描述小球在不同时刻的位置,
除了用一维坐标,还可以用什么呢?
o
x
o
x
o
x
位移 x x1 x2 x3 x4
时间 t t1 t2 t3 t4
x/cm
t/s
还可以列表、描点、连线
该图像不是小球的运动轨迹。
右边
左边
(1)请你拿起手中的笔,在白纸上方模拟水平弹簧振子在平衡位置附近左右往复运动,你会得到怎样的图像?
方法一:手动描图法
5. 怎么描绘振子的位移-时间( x-t )图像呢?
(2)一位同学匀速拉动白纸,另一同学沿与纸运动方向相垂直方向用笔往复画线段,你会得到怎样的图像?
再观察振子的运动
二、弹簧振子
记录数据
(以向右为正方向)
5. 怎么描绘振子的位移-时间( x-t )图像呢?
方法三:频闪照相法
二、弹簧振子
再观察振子的运动
t/s
x/mm
20
-20
10
-10
3t0
6t0
9t0
12t0
15t0
O
5. 怎么描绘振子的位移-时间( x-t )图像呢?
方法三:频闪照相法
二、弹簧振子
再观察振子的运动
列表、描点、连线
6. 怎么证明x - t图像是“正弦式”函数图像?
再观察振子的运动
二、弹簧振子
选取小球平衡位置为坐标原点,建立坐标系,横轴和纵轴分别表示时间t和小球的位移x。在坐标系中标出各时刻小球球心的位置,用曲线把各点连接起来,就是小球在平衡位置附近往复运动时的位移—时间图像,即x-t图像。x-t图像即振动图像。
从弹簧振子的x-t图像可以看出,小球位移与时间的关系似乎可以用正弦函数来表示。
6. 怎么证明x - t图像是“正弦式”函数图像?
再观察振子的运动
二、弹簧振子
方法一:利用数学函数表达式
假定图中的曲线是正弦曲线,测量它的振幅和周期,写出对应的正弦函数的表达式。
上图中,测量小球在各个位置的横坐标和纵坐标。把测量值输入计算机中,作出这条曲线,看一看小球的位移—时间关系是否可以用正弦函数表示。通过仔细分析会发现,小球位移与时间的关系是正弦函数关系。
方法二:利用计算机数值拟合
结论:水平弹簧振子的x-t图像是正弦函数图像。
如果质点的位移与时间的关系遵从正弦函数的规律,即它的振动图象(x-t 图象)是一条正弦曲线,
简谐运动是生活中最基本、最简单的振动,
这样的振动被称为简谐运动(simple harmonic motion)。
简谐运动:
例:水平弹簧振子
三、简谐运动
生活中的复杂振动都可以看成是很多简谐运动的合成。
B
C
由简谐运动的图像获取的信息
三、简谐运动
C
B
O
小球在BC之间来回运动,O为平衡位置。
B:正方向最大位移,速度为零,弹力最大;
C:负方向最大位移,速度为零,弹力最大;
位移 速度 弹簧弹力 加速度
B 负方向最大 零 最大 最大
O 零 最大 零 零
C 正方向最大 零 最大 最大
规定向右为正方向
过程 加速度大小变化 速度大小变化
A到O
O到B
B到O
O到B
衡位置时
远离平衡位置时
由简谐运动的图像获取的信息
三、简谐运动
B
C
C
B
O
规定向右为正方向
由简谐运动的图像获取的信息
三、简谐运动
(1)某一时刻质点的位移大小和方向:
质点在t1、t2时刻的位移分别为x1和-x2.
小球在BC之间来回运动,O为平衡位置。
B
C
C
B
O
规定向右为正方向
由简谐运动的图像获取的信息
三、简谐运动
如图中a点,下一时刻质点离平衡位置更远,故a点对应时刻质点向正方向远离平衡位置运动。
B
C
C
B
O
规定向右为正方向
(2)某一时刻质点的运动(速度)方向:
小球在BC之间来回运动,O为平衡位置。
由简谐运动的图像获取的信息
三、简谐运动
①观察下一时刻质点的位移:
(3)质点的速度、位移的变化情况:
小球在BC之间来回运动,O为平衡位置。
B
C
C
B
O
规定向右为正方向
若下一时刻远离平衡位置,则速度越来越小,位移越来越大;若衡位置,则速度越来越大,位移越来越小.
由简谐运动的图像获取的信息
三、简谐运动
②根据斜率判断速度的大小和方向:
斜率:
B
C
C
B
O
规定向右为正方向
(3)质点的速度、位移的变化情况:
小球在BC之间来回运动,O为平衡位置。
斜率越大,则速度越大,斜率越小,则速度越小;斜率为正,则速度沿正方向,斜率为负,则速度沿负方向.
四、复杂振动
心电图
x
t
四、复杂振动
例1. 如图是某质点做简谐运动的振动图像。根据图像中的信息,回答下列问题。
(1)质点离开平衡位置的最大距离有多大?
(2)在1.5s和2.5s这两个时刻,质点的位置在哪里?质点向哪个方向运动?
五、练习与应用
例1. 如图是某质点做简谐运动的振动图像。根据图像中的信息,回答下列问题。
(3)质点相对于平衡位置的位移方向在哪些时间内跟它的瞬时速度的方向相同?在哪些时间内跟瞬时速度的方向相反?
(4)质点在第2s末的位移是多少?
(5)质点在前2s内运动的路程是多少?
四、练习与应用
三、简谐运动
新课讲授
方法一:正弦函数代入法
(1)假定所得曲线是正弦曲线,测量它的振幅和周期,写出对应的正弦函数表达式;
(2)在图中选小球若干个位置,用刻度尺在图中测量增坐标,将每个位移对应的振动时间代入表达式求出函数值,比较这一函数值与测量值,看是否相等,若可视为相等,则这条曲线就是正弦曲线。
三、简谐运动
新课讲授
方法二:计算机函数图像耦合法
