展开与折叠[上学期]

课件22张PPT。展开与折叠(1)情境创设:
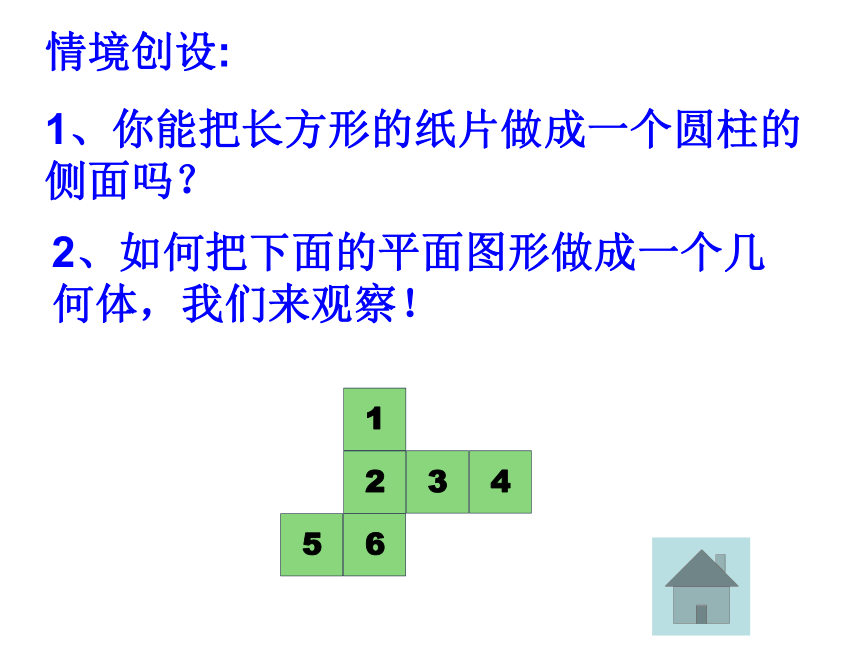
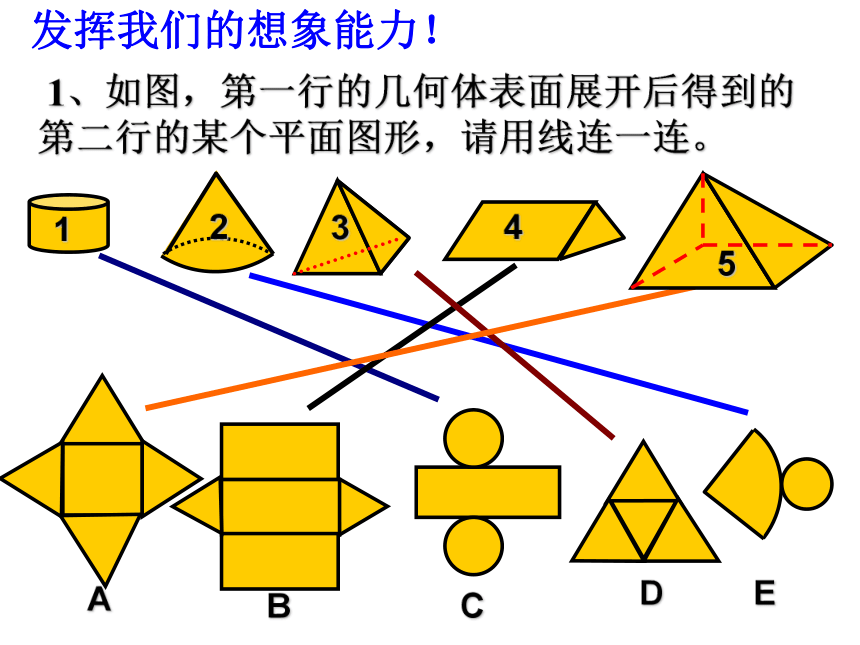
1、你能把长方形的纸片做成一个圆柱的侧面吗？2、如何把下面的平面图形做成一个几何体，我们来观察！ 1、如图，第一行的几何体表面展开后得到的第二行的某个平面图形，请用线连一连。发挥我们的想象能力！思考：
棱柱的侧面都是 。
棱锥的侧面都是 。
棱锥的展开图中至少有 三角形。
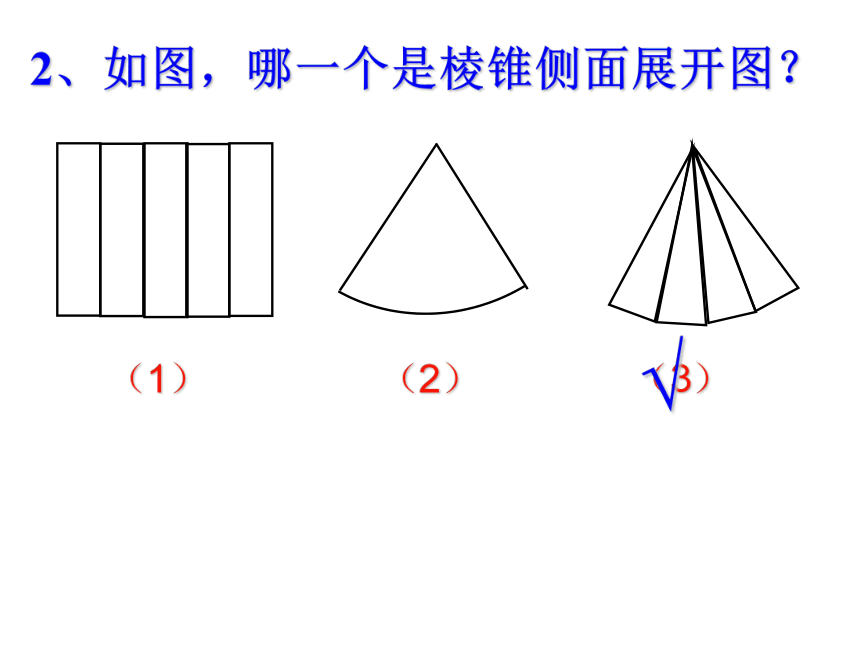
棱柱的展开图中至多有 三角形。归纳：我们可以根据展开图各部分的形状和个数来判断是棱柱还是棱锥，到底是几棱柱还是几棱锥。长方形三角形四两2、如图，哪一个是棱锥侧面展开图？（1）（2）（3）√合作探究:（三人一小组）1、你们能将一个正方体沿棱剪成一个平面图形吗？ 三人合作，拿出一个正方体随便剪，尝试一下。提醒：
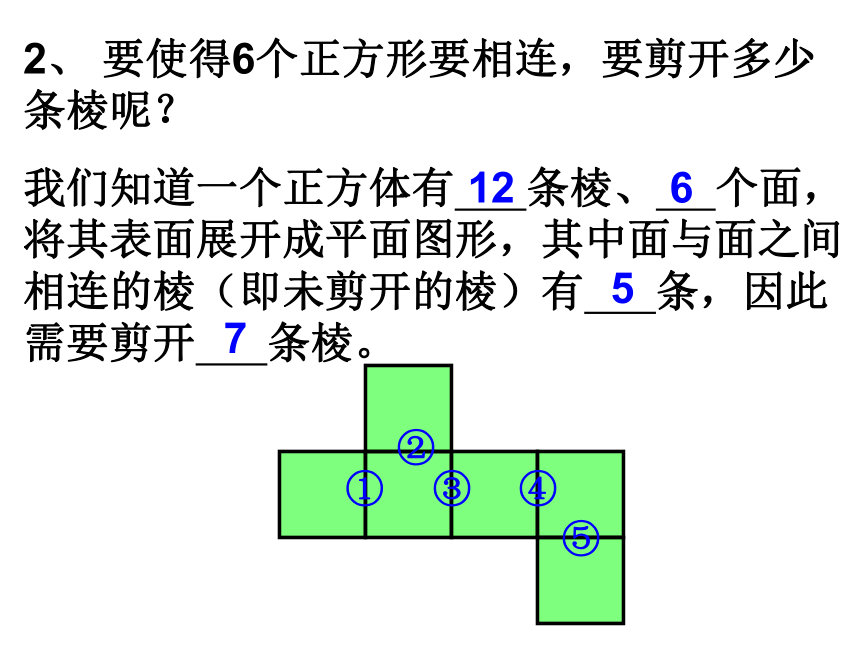
正方体的表面展开的6个正方形中的每一个正方形至少要有一条边与其他的正方形的边相连，即这6个正方形要相连。2、 要使得6个正方形要相连，要剪开多少条棱呢？
我们知道一个正方体有 条棱、 个面，将其表面展开成平面图形，其中面与面之间相连的棱（即未剪开的棱）有 条，因此需要剪开 条棱。
126573、同一个正方体纸盒的表面沿不同的棱剪开，展开成的平面图形是否相同？4、三人共同讨论合作一起裁剪，在裁剪的过程中注意：①如何剪；②这样剪行吗？③下一步又怎样剪？
看哪个小组在短时间内，剪成的表面展开图既多又不同！思考：
一个正方体到底有多少种形状的平面展开图？正方体的表面展开图(11种) 第一类，中间四连方，两侧各一个，共六种。简称“一四一” 第二类，中间三连方，两侧各有一、二个，共三种。简称“一三二”或“二三一”第三类，阶梯状，共两种。两排各三个。简称“三三”中间二连方，两侧各有二个。简称“二二二”难点突破： 以下图形无法折叠成正方体，请记住！一字形田字格凹字形凸宝盖“L”形一二三 1、下图不是正方体的表面展开图是（ ）ADCBD练习巩固: 2、下面六个正方形连在一起的图形，经折叠后能围成正方体的图形有哪几个？GFEDCBA3、下面哪些图形经过折叠可以围成一个棱柱？（1） （2）　　　　　　　　　（３）　　　　　　　　　（４） （５） （６） 小壁虎的难题：
如图：一只圆桶的下方有一只壁虎，上方有一只蚊子，壁虎要想尽快吃到蚊子，应该走哪条路径？你有何高招？综合应用： 如图，一只蚂蚁，在正方体箱子的一个顶点A，它发现相距它最远的另一个顶点B处有它感兴趣的食物，这只蚂蚁想尽快得到食物，哪条路径最短？试在图中将路线画出来。小结：１、有些平面图形一些立体图形展开２、圆柱的侧面展开图是长方形；圆锥的侧面展开图是扇形。
３、通过侧面展开图的形状判断原几何体是棱柱还是棱锥。
４、（难点）正方体的展开图的形状（共11种）；（突破难点）识记不能折叠成正方体的平面图形的形状（共６种） 。