人教版二年级数学下册 第三单元第3课时《解决问题》(表格式教案)
文档属性
| 名称 | 人教版二年级数学下册 第三单元第3课时《解决问题》(表格式教案) | 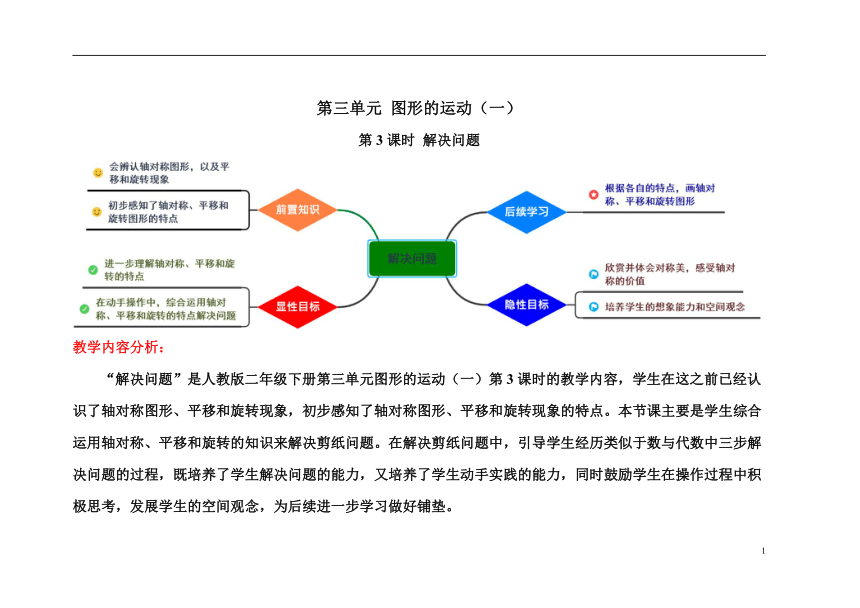 | |
| 格式 | docx | ||
| 文件大小 | 293.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 21:34:07 | ||
图片预览



文档简介
第三单元 图形的运动(一)
第3课时 解决问题
教学内容分析:
“解决问题”是人教版二年级下册第三单元图形的运动(一)第3课时的教学内容,学生在这之前已经认识了轴对称图形、平移和旋转现象,初步感知了轴对称图形、平移和旋转现象的特点。本节课主要是学生综合运用轴对称、平移和旋转的知识来解决剪纸问题。在解决剪纸问题中,引导学生经历类似于数与代数中三步解决问题的过程,既培养了学生解决问题的能力,又培养了学生动手实践的能力,同时鼓励学生在操作过程中积极思考,发展学生的空间观念,为后续进一步学习做好铺垫。
教学目标:
1. 进一步理解轴对称、平移和旋转的特点。
2. 在动手操作中,综合运用轴对称、平移和旋转的特点解决问题。
3. 欣赏并体会对称美,感受轴对称的价值,培养学生的想象能力和空间观念。
教学重点:
认识轴对称图形的特点、平移现象和旋转现象,建立概念。
教学难点:
准确判断哪些是轴对称图形,利用平移现象解决问题。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 1.关于图形的运动,你有了哪些认识? 根据学生回答课件出示特点。 2.剪纸作为一种非常普及的民间装饰艺术,已经入选国家非物质文化遗产。(课件出示)轴对称、平移和旋转在剪纸中有着广泛的运用。 3.今天这节课我们就要用轴对称、平移、旋转的知识,在想一想、剪一剪的活动中解决问题。 学生回答: 我认识了轴对称图形、平移和旋转现象。 我知道轴对称图形对折后能够完全重合。 我知道平移前后,都是沿着直的路线移动,大小、形状和方向不变。 我知道旋转是绕着中心转动,物体的每个部分都绕着一个点转动,大小、形状不变。 从复习轴对称图形、平移和旋转现象特点引入,一方面回顾上节课所学,另一方面为接下来解决剪纸问题作好铺垫。特别是剪纸欣赏,激发学生剪纸的兴趣。
环节二 探究新知 1.出示例4:你能剪出像下面这样手拉手的4个小人吗? (1)读一读,看一看,你知道了什么? (2)那应该怎么剪呢? (3)嗯,看来剪一个难不倒大家。(课件出示)只要对折后画出半个小人,剪下来就可以了。 (4)剪4个比较困难,那么我们可以根据刚才剪一个的方法,试着剪2个小人。 (5)请你边做边说,你是怎么剪的? 根据学生的回答课件出示,介绍过程。 (6)(课件出示错误)那为什么会剪出这样左右半个小人呢?根据学生回答课件呈现错误画法。 (7)那应该怎么画这半个小人? 对啦!两个小人有两条对称轴,画半个小人的时候,应该画在有两条对称轴这一边,也就是全部连在一起的这边。(课件出示) (8)当然,折纸的方法不止一种,还可以这样折。(课件出示) (9)现在你能剪出像下面这样手拉手的4个小人吗?试一试。 ①师巡视,指导有困难的。 ②谁来说一说,你是怎么剪的? ③为什么要对折三次啊? ④你很会思考。我们一起来回顾一下。(课件出示)对折一次,剪出1个小人,对折两次,剪出2个小人,对折3次,剪出4个小人。 ⑤你们都画成功了吗?那画小人的需要注意什么?根据学生回答课件出示。 ⑥其实折纸的方法不止一种,还可以这样折。(课件出示),画半个小人也是画在有4条折痕这边,也就是全部连在一起的这边。 2.想一想,找一找规律。 (1)对折一次剪出1个小人,对折两次剪出2个小人,对折三次剪出4个小人,那要剪出8个小人,需要对折几次?为什么? (2)那对折5次可以剪出几个小人?为什么? (3)看来,大家都已经发现对折次数和小人个数之间的规律了。在解决问题的过程中,思考会帮助我们把复杂问题简单化。 学生读题思考。 学生回答 生1:每个小人都是轴对称图形。 生2:4个小人也是轴对称图形。 生3:这4个小人是一样的,而且还连在一起。 生:我只会剪一个,剪4个还没想好。 学生动手剪一剪。 学生边操作边理解 生:把这张纸连续对折两次,画出半个小人,剪下来就是手拉手的2个小人。 因为半个小人的位置画错了。 生:应该画在这张纸有两条折痕的一边。 学生尝试剪一剪。 生:我先对折三次,然后画半个小人,剪下来就成功了。 生:对折一次是1个小人,对折两次是2个小人。那么再对折一次,就是2个变4个,所以我对折了三次。 在画半个小人的时候,需要画在全部连在一起的这边。 生:需要对折4次。因为对折增加一次,小人的数量就是前面的2倍。8个小人是前面4个小人的2倍,因此只要在对折3次的基础上再对折一次,也就是对折4次。 生:可以剪出16个小人。因为对折5次就是在对折4次的基础上再增加一次,那么小人数量就是对折4次小人数量的2倍,是8个小人的2倍,也就是16个小人。 围绕解决剪4个手拉手的小人这个问题,引导学生先从剪一个小人入手,再剪2个小人,最后剪4个小人,渗透“化繁为简”的数学思想。在学生剪一剪的过程中,不断对折纸、画图进行分析思考,在讨论和交流的过程中,逐步掌握剪4个小人的正确方法。 同时,通过观察和思考,发现了对折次数和小人个数之间的规律,有效提升了学生的数学思维。
环节三 巩固练习 练习1:看一看,连一连。 (1)指名学生说。 (2)根据学生回答课件出示。 练习2:想一想,连一连。 (1)按照左图的方法,对折两次。剪法1,从右上角剪去一个三角形。剪法2,从右下角剪去一个三角形。剪法1得到的图案是哪一个?你是怎么想的?根据学生回答连线。 (2)那剪法2得到的是图案(1)吗?为什么? (3)要正确判断,观察和思考很重要。我们要根据折纸和剪纸的方法进行分析判断。 练习3:折一折,剪一剪。 (1)观察这个图案,与刚才的有什么不同? (2)那你准备怎么折?怎么剪?请你试一试。 (3)说一说,你是怎么折?怎么剪的? (4)师介绍剪法。先斜对折,再对折两次,把小人画在连一起这边。(课件出示) (5)多思考,多尝试就能找到解决问题的方法。 生:上面第1个连下面第2个,上面第2个连下面第3个,上面第3个连下面第1个。 生:剪法1的得到的图案(2)。因为剪法1剪去的三角形是4层连在一起的,打开后中间正好是一个正方形。 生:剪法2得到的是图案(1)。因为剪法2剪去的三角形上面2层与下面2层是分开的,打开后是两个大三角形。 学生回答 生1:这里的4个小人不仅手拉手,还头连头。 生2:刚才的4个小人,可以看成是由第1个小人平移得到,而这里的4个小人是由一个小人旋转得到的。 生3:这个图像上下对折,左右对折,斜对角对折都是能够重合的。 生:斜对折三次,得到一个三角形。然后画半个小人剪一剪。 通过练习,培养学生想象能力,发展空间观念。特别是变式练习剪手拉手,头连头的4个小人,一方面有助于学生利用刚才的所学解决新问题,另一方面问题要求的改变,又一次激发了学生的深度思考,有效提升了空间想象能力。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 1.学会了用轴对称、平移和旋转知识解决剪纸问题。 2.剪纸前需要多思考,多分析。 鼓励学生畅谈自己的收获和体会,贯通前后的知识。
环节五 拓展延伸 剪纸设计:用轴对称、平移和旋转的知识设计。 要设计一副剪纸作品,需要分哪几步? 学生回答 折——画——剪——展开 学生动手设计。 激发学生剪纸的兴趣,提升动手操作能力。
1
第3课时 解决问题
教学内容分析:
“解决问题”是人教版二年级下册第三单元图形的运动(一)第3课时的教学内容,学生在这之前已经认识了轴对称图形、平移和旋转现象,初步感知了轴对称图形、平移和旋转现象的特点。本节课主要是学生综合运用轴对称、平移和旋转的知识来解决剪纸问题。在解决剪纸问题中,引导学生经历类似于数与代数中三步解决问题的过程,既培养了学生解决问题的能力,又培养了学生动手实践的能力,同时鼓励学生在操作过程中积极思考,发展学生的空间观念,为后续进一步学习做好铺垫。
教学目标:
1. 进一步理解轴对称、平移和旋转的特点。
2. 在动手操作中,综合运用轴对称、平移和旋转的特点解决问题。
3. 欣赏并体会对称美,感受轴对称的价值,培养学生的想象能力和空间观念。
教学重点:
认识轴对称图形的特点、平移现象和旋转现象,建立概念。
教学难点:
准确判断哪些是轴对称图形,利用平移现象解决问题。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 1.关于图形的运动,你有了哪些认识? 根据学生回答课件出示特点。 2.剪纸作为一种非常普及的民间装饰艺术,已经入选国家非物质文化遗产。(课件出示)轴对称、平移和旋转在剪纸中有着广泛的运用。 3.今天这节课我们就要用轴对称、平移、旋转的知识,在想一想、剪一剪的活动中解决问题。 学生回答: 我认识了轴对称图形、平移和旋转现象。 我知道轴对称图形对折后能够完全重合。 我知道平移前后,都是沿着直的路线移动,大小、形状和方向不变。 我知道旋转是绕着中心转动,物体的每个部分都绕着一个点转动,大小、形状不变。 从复习轴对称图形、平移和旋转现象特点引入,一方面回顾上节课所学,另一方面为接下来解决剪纸问题作好铺垫。特别是剪纸欣赏,激发学生剪纸的兴趣。
环节二 探究新知 1.出示例4:你能剪出像下面这样手拉手的4个小人吗? (1)读一读,看一看,你知道了什么? (2)那应该怎么剪呢? (3)嗯,看来剪一个难不倒大家。(课件出示)只要对折后画出半个小人,剪下来就可以了。 (4)剪4个比较困难,那么我们可以根据刚才剪一个的方法,试着剪2个小人。 (5)请你边做边说,你是怎么剪的? 根据学生的回答课件出示,介绍过程。 (6)(课件出示错误)那为什么会剪出这样左右半个小人呢?根据学生回答课件呈现错误画法。 (7)那应该怎么画这半个小人? 对啦!两个小人有两条对称轴,画半个小人的时候,应该画在有两条对称轴这一边,也就是全部连在一起的这边。(课件出示) (8)当然,折纸的方法不止一种,还可以这样折。(课件出示) (9)现在你能剪出像下面这样手拉手的4个小人吗?试一试。 ①师巡视,指导有困难的。 ②谁来说一说,你是怎么剪的? ③为什么要对折三次啊? ④你很会思考。我们一起来回顾一下。(课件出示)对折一次,剪出1个小人,对折两次,剪出2个小人,对折3次,剪出4个小人。 ⑤你们都画成功了吗?那画小人的需要注意什么?根据学生回答课件出示。 ⑥其实折纸的方法不止一种,还可以这样折。(课件出示),画半个小人也是画在有4条折痕这边,也就是全部连在一起的这边。 2.想一想,找一找规律。 (1)对折一次剪出1个小人,对折两次剪出2个小人,对折三次剪出4个小人,那要剪出8个小人,需要对折几次?为什么? (2)那对折5次可以剪出几个小人?为什么? (3)看来,大家都已经发现对折次数和小人个数之间的规律了。在解决问题的过程中,思考会帮助我们把复杂问题简单化。 学生读题思考。 学生回答 生1:每个小人都是轴对称图形。 生2:4个小人也是轴对称图形。 生3:这4个小人是一样的,而且还连在一起。 生:我只会剪一个,剪4个还没想好。 学生动手剪一剪。 学生边操作边理解 生:把这张纸连续对折两次,画出半个小人,剪下来就是手拉手的2个小人。 因为半个小人的位置画错了。 生:应该画在这张纸有两条折痕的一边。 学生尝试剪一剪。 生:我先对折三次,然后画半个小人,剪下来就成功了。 生:对折一次是1个小人,对折两次是2个小人。那么再对折一次,就是2个变4个,所以我对折了三次。 在画半个小人的时候,需要画在全部连在一起的这边。 生:需要对折4次。因为对折增加一次,小人的数量就是前面的2倍。8个小人是前面4个小人的2倍,因此只要在对折3次的基础上再对折一次,也就是对折4次。 生:可以剪出16个小人。因为对折5次就是在对折4次的基础上再增加一次,那么小人数量就是对折4次小人数量的2倍,是8个小人的2倍,也就是16个小人。 围绕解决剪4个手拉手的小人这个问题,引导学生先从剪一个小人入手,再剪2个小人,最后剪4个小人,渗透“化繁为简”的数学思想。在学生剪一剪的过程中,不断对折纸、画图进行分析思考,在讨论和交流的过程中,逐步掌握剪4个小人的正确方法。 同时,通过观察和思考,发现了对折次数和小人个数之间的规律,有效提升了学生的数学思维。
环节三 巩固练习 练习1:看一看,连一连。 (1)指名学生说。 (2)根据学生回答课件出示。 练习2:想一想,连一连。 (1)按照左图的方法,对折两次。剪法1,从右上角剪去一个三角形。剪法2,从右下角剪去一个三角形。剪法1得到的图案是哪一个?你是怎么想的?根据学生回答连线。 (2)那剪法2得到的是图案(1)吗?为什么? (3)要正确判断,观察和思考很重要。我们要根据折纸和剪纸的方法进行分析判断。 练习3:折一折,剪一剪。 (1)观察这个图案,与刚才的有什么不同? (2)那你准备怎么折?怎么剪?请你试一试。 (3)说一说,你是怎么折?怎么剪的? (4)师介绍剪法。先斜对折,再对折两次,把小人画在连一起这边。(课件出示) (5)多思考,多尝试就能找到解决问题的方法。 生:上面第1个连下面第2个,上面第2个连下面第3个,上面第3个连下面第1个。 生:剪法1的得到的图案(2)。因为剪法1剪去的三角形是4层连在一起的,打开后中间正好是一个正方形。 生:剪法2得到的是图案(1)。因为剪法2剪去的三角形上面2层与下面2层是分开的,打开后是两个大三角形。 学生回答 生1:这里的4个小人不仅手拉手,还头连头。 生2:刚才的4个小人,可以看成是由第1个小人平移得到,而这里的4个小人是由一个小人旋转得到的。 生3:这个图像上下对折,左右对折,斜对角对折都是能够重合的。 生:斜对折三次,得到一个三角形。然后画半个小人剪一剪。 通过练习,培养学生想象能力,发展空间观念。特别是变式练习剪手拉手,头连头的4个小人,一方面有助于学生利用刚才的所学解决新问题,另一方面问题要求的改变,又一次激发了学生的深度思考,有效提升了空间想象能力。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 1.学会了用轴对称、平移和旋转知识解决剪纸问题。 2.剪纸前需要多思考,多分析。 鼓励学生畅谈自己的收获和体会,贯通前后的知识。
环节五 拓展延伸 剪纸设计:用轴对称、平移和旋转的知识设计。 要设计一副剪纸作品,需要分哪几步? 学生回答 折——画——剪——展开 学生动手设计。 激发学生剪纸的兴趣,提升动手操作能力。
1
