人教版数学八年级下册第十八章平行四边形 单元练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册第十八章平行四边形 单元练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 330.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 15:02:01 | ||
图片预览




文档简介
第十八章 平行四边形
一、单选题
1.下列命题是假命题的是( )
A.直角三角形中,30°角所对的直角边等于斜边的一半
B.三角形三条边的垂直平分线的交点到三角形的三个顶点的距离相等
C.平行四边形是中心对称图形
D.对角线相等的四边形是平行四边形
2.若菱形的两条对角线长分别为8和6,则这个菱形的面积是( )
A.96 B.48 C.24 D.12
3.下列说法不正确的是( )
A.平行四边形两组对边分别平行 B.平行四边形的对角线互相平分
C.平行四边形的对角互补,邻角相等 D.平行四边形的两组对边分别相等
4.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( ).
A.20 B.15 C.10 D.5
5.已知下列命题
①一组对边平行且相等的四边形是平行四边形;
②两条对角线互相垂直且相等的四边形是正方形;
③一组对边平行且两条对角线相等的四边形是矩形;
④两条对角线互相垂直的平行四边形是菱形.
其中正确的命题的个数是( )
A.0 B.1 C.2 D.3
6.如图,D,E分别是AB,AC的中点,BE是∠ABC的平分线,对于下列结论:①BC=2DE;②DE∥BC;③BD=DE;④BE⊥AC.其中正确的是 ( )
A.①② B.①②③ C.①②④ D.①②③④
7.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有 ( ).
A.1个 B.2个 C.3个 D.4个
8.如图,正方形的对角线与相交于点O,的角平分线分别交、于M、N点.若,则线段的长为( )
A. B. C.1 D.
9.下列命题是真命题的为( )
A.若一个四边形的四个角的平分线能围成一个矩形,则这个四边形是矩形
B.若顺次连接一个四边形的中点所得的四边形是正方形,则这个四边形也是正方形
C.若一个四边形的四个角的平分线能围成一个正方形,则这个四边形是矩形
D.若一个四边形的四个角的平分线能围成一个正方形,则这个四边形也是正方形
10.正方形ABCD中,E为BC的中点,连接AE,过点D作于点G,延长DG交AB于点F,连接CG并延长交AB于点I,过点B作于点H,连接DH,CH.则以下结论中:①且;②;③;④.正确的结论有( )个.
A.1 B.2 C.3 D.4
二、填空题
11.平行四边形的周长为24cm,相邻两边长的比为3:1,那么这个平行四边形较短的边长为_____cm.
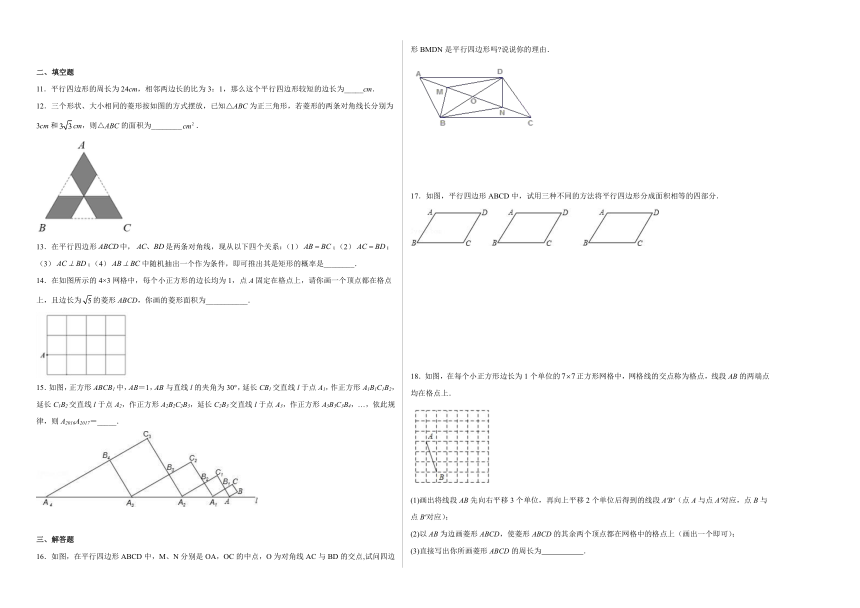
12.三个形状、大小相同的菱形按如图的方式摆放,已知△ABC为正三角形,若菱形的两条对角线长分别为3cm和cm,则△ABC的面积为________.
13.在平行四边形中,是两条对角线,现从以下四个关系:(1);(2);(3);(4)中随机抽出一个作为条件,即可推出其是矩形的概率是________.
14.在如图所示的4×3网格中,每个小正方形的边长均为1,点A固定在格点上,请你画一个顶点都在格点上,且边长为的菱形ABCD,你画的菱形面积为___________.
15.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2016A2017=_____.
三、解答题
16.如图,在平行四边形ABCD中,M、N分别是OA,OC的中点,O为对角线AC与BD的交点,试问四边形BMDN是平行四边形吗 说说你的理由.
17.如图,平行四边形ABCD中,试用三种不同的方法将平行四边形分成面积相等的四部分.
18.如图,在每个小正方形边长为1个单位的正方形网格中,网格线的交点称为格点,线段AB的两端点均在格点上.
(1)画出将线段AB先向右平移3个单位,再向上平移2个单位后得到的线段A'B'(点A与点A'对应,点B与点B'对应);
(2)以AB为边画菱形ABCD,使菱形ABCD的其余两个顶点都在网格中的格点上(画出一个即可);
(3)直接写出你所画菱形ABCD的周长为 .
参考答案:
1.D
【详解】解:A、直角三角形中,30°角所对的直角边等于斜边的一半,正确,是真命题;
B、三角形三条边的垂直平分线的交点到三角形的三个顶点的距离相等,正确,是真命题;
C、平行四边形是中心对称图形,正确,是真命题;
D、对角线互相平分的四边形是平行四边形,故原命题错误,是假命题,
故选D.
2.C
【详解】解:∵四边形ABCD是菱形,
∴S=×6×8=24.
故选:C.
3.C
【详解】解:A.平行四边形两组对边分别平行,原说法正确,故该项不符合题意;
B.平行四边形的对角线互相平分,原说法正确,故该项不符合题意;
C.平行四边形的对角相等,邻角互补,原说法不正确,故该项符合题意;
D.平行四边形的两组对边分别相等,原说法正确,故该项不符合题意;
故选:C.
4.B
【详解】∵ABCD是菱形,∠BCD=120°,
∴∠B=60°,BA=BC.
∴△ABC是等边三角形.
∴△ABC的周长=3AB=15.
故选B.
5.C
【详解】解:①∵一组对边平行且相等的四边形是平行四边形;
∴故本选项正确;
②∵两条对角线互相垂直且相等的四边形不一定是平行四边形,
∴故本选项错误;
③∵一组对边平行且两条对角线相等的四边形可能是等腰梯形.
∴故本选项错误;
④∵两条对角线互相垂直的平行四边形是菱形.
∴故本选项正确.
故选:C.
6.D
【详解】∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,DE∥BC,①、②正确;
∵DE∥BC,
∴∠DEB=∠EBC,
∵BE是∠ABC的平分线,
∴∠DBE=∠EBC,
∴∠DEB=∠EBD,
∴BD=DE,③正确;
∵点E是AC的中点,BE是∠ABC的平分线,
∴BE⊥AC,④正确;
故选D.
7.B
【详解】试题分析:已知∠APE、∠CPF都是∠APF的余角,可得∠APE=∠CPF,又因AB=AC,∠BAC=90°,P是BC中点,可得AP=CP,所以∠PAE=∠PCF,即可得△APE≌△CPF(ASA),同理可证△APF≌△BPE,所以AE=CF,△EPF是等腰直角三角形,S四边形AEPF=S△ABC,①②正确,③不正确;而AP=BC,当EF不是△ABC的中位线时,则EF不等于BC的一半,EF=AP故④不成立.所以始终正确的是①②.故答案选B.
考点:全等三角形的判定及性质;三角形的中位线的性质的运用.
8.D
【详解】作于H,如图,
∵四边形为正方形,
∴,
∴为等腰直角三角形,
∵,
∴,
∵平分,,
∴,,
∵,
∴,
∵,
∴,
∴,
故选D.
9.C
【详解】解:A、若一个四边形的四个角的平分线能围成一个矩形,则这个四边形是平行四边形,不一定是矩形,如图,故A选项错误;
B、顺次连接一个四边形的中点所得的四边形是正方形,则这个四边形的对角线相等且互相垂直,但这个四边形不一定是正方形,如图,故B选项错误;
C、若一个四边形的四个角的平分线能围成一个正方形,则这个四边形是矩形,如图,故C选项正确;
D、若一个四边形的四个角的平分线能围成一个正方形,则这个四边形是矩形,不一定是正方形,故D选项错误;
故选:C.
10.B
【详解】解:如图,连接FH,DE,取AD的中点T,连接FT,CT.
∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠BAF=∠ABE=90°,
∵DF⊥AE,
∴∠BAE+∠DAE=90°,∠DAE+∠ADF=90°,
∴∠ADF=∠BAE,
在△DAF和△ABE中,
,
∴△DAF≌△ABE(ASA),
∴AF=BE,
∵CE=EB=CB,
∴AF=AB,
∴AF=BF,
∴FA=FH,
∵FG⊥AH,
∴AG=GH,
∴DH=AD,
∵AT=DT=CE=BE,ATEC,
∴四边形AECT是平行四边形,
∴AECT,
∴CT⊥DF,
同法可证CD=CG,
∴DH=CG,
∴∠CDG=∠CGD,
∵∠CGE+∠CGD=90°,∠CDG+∠ADG=90°,
∴∠CGE=∠ADF=∠BAE,
∵∠AGI=∠CGE,
∴∠IAG=∠IGA,
∵∠DAH=∠DHA,∠GAI+∠DAG=90°,
∴∠CGE+∠AHD=90°,
∴∠GJH=90°,
∴DH⊥CG,故①正确,
∵∠IAG+∠AFG=90°,∠IGA+∠IGF=90°,
∴∠IFG=∠IFG,
∴IA=IG=IF=AF=AB,故②正确,
设BE=EC=m,则AB=BC=2m,AE=m,
过点H作HR⊥BC于点R,HW⊥CD于点W,
∵BH⊥AE,
∴,
∴,
同法,
∴,
∴,
∴,故③错误,
∵四边形HRCW是矩形,
∴,
∴,故④错误.
故选:B.
11‘平行四边形对边相等,周长为24cm,相邻两边长的比为3:1,则设邻边为
,
解得,
即这个平行四边形较短的边长为3cm,
故答案为:3.
12.∵为正三角形,∴,
∵菱形的两条对角线长分别为3cm和cm,∴菱形的边长为3cm,
∴AB=BC=AC=3×3=9(cm),
∴三角形的高(cm),
∴,
故答案为:.
13.可推出平行四边形ABCDABCD是矩形有②④,概率为.
14.
解:如图所示(画一个即可)
故答案为: 5或4.
15.∵四边形ABCB 是正方形,
∴AB=AB ,AB∥CB ,
∴AB∥A C,
∴∠CA A=30°,
∴A B =,AA =2,
∴A B =A B =,
∴A A =2,
同理:A A =2() ,
=2() ,
…
∴
∴
故答案为
16.∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
∵ M、N分别是OA,OC的中点
∴OM=ON
∴四边形BMDN是平行四边形.
17方法一:找出平行四边形的左右两条边的四等分点,依次对应连接起来,即可将平行四边形四等分;
方法二:连接平行四边形的两组对边的中点,即可把平行四边形四等分;
方法三:连接平行四边形的两条对角线,即可把平行四边形四等分;据此即可画图.
试题分析:如图所示:
18.
(1)
平移变换的性质分别作出A,B的对应点A′、B′,
如图,段A'B'即为所求:
(2)
如图所示,菱形ABCD即为所求,答案不唯一;
(3)
,
∴菱形ABCD的周长=.
一、单选题
1.下列命题是假命题的是( )
A.直角三角形中,30°角所对的直角边等于斜边的一半
B.三角形三条边的垂直平分线的交点到三角形的三个顶点的距离相等
C.平行四边形是中心对称图形
D.对角线相等的四边形是平行四边形
2.若菱形的两条对角线长分别为8和6,则这个菱形的面积是( )
A.96 B.48 C.24 D.12
3.下列说法不正确的是( )
A.平行四边形两组对边分别平行 B.平行四边形的对角线互相平分
C.平行四边形的对角互补,邻角相等 D.平行四边形的两组对边分别相等
4.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( ).
A.20 B.15 C.10 D.5
5.已知下列命题
①一组对边平行且相等的四边形是平行四边形;
②两条对角线互相垂直且相等的四边形是正方形;
③一组对边平行且两条对角线相等的四边形是矩形;
④两条对角线互相垂直的平行四边形是菱形.
其中正确的命题的个数是( )
A.0 B.1 C.2 D.3
6.如图,D,E分别是AB,AC的中点,BE是∠ABC的平分线,对于下列结论:①BC=2DE;②DE∥BC;③BD=DE;④BE⊥AC.其中正确的是 ( )
A.①② B.①②③ C.①②④ D.①②③④
7.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有 ( ).
A.1个 B.2个 C.3个 D.4个
8.如图,正方形的对角线与相交于点O,的角平分线分别交、于M、N点.若,则线段的长为( )
A. B. C.1 D.
9.下列命题是真命题的为( )
A.若一个四边形的四个角的平分线能围成一个矩形,则这个四边形是矩形
B.若顺次连接一个四边形的中点所得的四边形是正方形,则这个四边形也是正方形
C.若一个四边形的四个角的平分线能围成一个正方形,则这个四边形是矩形
D.若一个四边形的四个角的平分线能围成一个正方形,则这个四边形也是正方形
10.正方形ABCD中,E为BC的中点,连接AE,过点D作于点G,延长DG交AB于点F,连接CG并延长交AB于点I,过点B作于点H,连接DH,CH.则以下结论中:①且;②;③;④.正确的结论有( )个.
A.1 B.2 C.3 D.4
二、填空题
11.平行四边形的周长为24cm,相邻两边长的比为3:1,那么这个平行四边形较短的边长为_____cm.
12.三个形状、大小相同的菱形按如图的方式摆放,已知△ABC为正三角形,若菱形的两条对角线长分别为3cm和cm,则△ABC的面积为________.
13.在平行四边形中,是两条对角线,现从以下四个关系:(1);(2);(3);(4)中随机抽出一个作为条件,即可推出其是矩形的概率是________.
14.在如图所示的4×3网格中,每个小正方形的边长均为1,点A固定在格点上,请你画一个顶点都在格点上,且边长为的菱形ABCD,你画的菱形面积为___________.
15.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2016A2017=_____.
三、解答题
16.如图,在平行四边形ABCD中,M、N分别是OA,OC的中点,O为对角线AC与BD的交点,试问四边形BMDN是平行四边形吗 说说你的理由.
17.如图,平行四边形ABCD中,试用三种不同的方法将平行四边形分成面积相等的四部分.
18.如图,在每个小正方形边长为1个单位的正方形网格中,网格线的交点称为格点,线段AB的两端点均在格点上.
(1)画出将线段AB先向右平移3个单位,再向上平移2个单位后得到的线段A'B'(点A与点A'对应,点B与点B'对应);
(2)以AB为边画菱形ABCD,使菱形ABCD的其余两个顶点都在网格中的格点上(画出一个即可);
(3)直接写出你所画菱形ABCD的周长为 .
参考答案:
1.D
【详解】解:A、直角三角形中,30°角所对的直角边等于斜边的一半,正确,是真命题;
B、三角形三条边的垂直平分线的交点到三角形的三个顶点的距离相等,正确,是真命题;
C、平行四边形是中心对称图形,正确,是真命题;
D、对角线互相平分的四边形是平行四边形,故原命题错误,是假命题,
故选D.
2.C
【详解】解:∵四边形ABCD是菱形,
∴S=×6×8=24.
故选:C.
3.C
【详解】解:A.平行四边形两组对边分别平行,原说法正确,故该项不符合题意;
B.平行四边形的对角线互相平分,原说法正确,故该项不符合题意;
C.平行四边形的对角相等,邻角互补,原说法不正确,故该项符合题意;
D.平行四边形的两组对边分别相等,原说法正确,故该项不符合题意;
故选:C.
4.B
【详解】∵ABCD是菱形,∠BCD=120°,
∴∠B=60°,BA=BC.
∴△ABC是等边三角形.
∴△ABC的周长=3AB=15.
故选B.
5.C
【详解】解:①∵一组对边平行且相等的四边形是平行四边形;
∴故本选项正确;
②∵两条对角线互相垂直且相等的四边形不一定是平行四边形,
∴故本选项错误;
③∵一组对边平行且两条对角线相等的四边形可能是等腰梯形.
∴故本选项错误;
④∵两条对角线互相垂直的平行四边形是菱形.
∴故本选项正确.
故选:C.
6.D
【详解】∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,DE∥BC,①、②正确;
∵DE∥BC,
∴∠DEB=∠EBC,
∵BE是∠ABC的平分线,
∴∠DBE=∠EBC,
∴∠DEB=∠EBD,
∴BD=DE,③正确;
∵点E是AC的中点,BE是∠ABC的平分线,
∴BE⊥AC,④正确;
故选D.
7.B
【详解】试题分析:已知∠APE、∠CPF都是∠APF的余角,可得∠APE=∠CPF,又因AB=AC,∠BAC=90°,P是BC中点,可得AP=CP,所以∠PAE=∠PCF,即可得△APE≌△CPF(ASA),同理可证△APF≌△BPE,所以AE=CF,△EPF是等腰直角三角形,S四边形AEPF=S△ABC,①②正确,③不正确;而AP=BC,当EF不是△ABC的中位线时,则EF不等于BC的一半,EF=AP故④不成立.所以始终正确的是①②.故答案选B.
考点:全等三角形的判定及性质;三角形的中位线的性质的运用.
8.D
【详解】作于H,如图,
∵四边形为正方形,
∴,
∴为等腰直角三角形,
∵,
∴,
∵平分,,
∴,,
∵,
∴,
∵,
∴,
∴,
故选D.
9.C
【详解】解:A、若一个四边形的四个角的平分线能围成一个矩形,则这个四边形是平行四边形,不一定是矩形,如图,故A选项错误;
B、顺次连接一个四边形的中点所得的四边形是正方形,则这个四边形的对角线相等且互相垂直,但这个四边形不一定是正方形,如图,故B选项错误;
C、若一个四边形的四个角的平分线能围成一个正方形,则这个四边形是矩形,如图,故C选项正确;
D、若一个四边形的四个角的平分线能围成一个正方形,则这个四边形是矩形,不一定是正方形,故D选项错误;
故选:C.
10.B
【详解】解:如图,连接FH,DE,取AD的中点T,连接FT,CT.
∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠BAF=∠ABE=90°,
∵DF⊥AE,
∴∠BAE+∠DAE=90°,∠DAE+∠ADF=90°,
∴∠ADF=∠BAE,
在△DAF和△ABE中,
,
∴△DAF≌△ABE(ASA),
∴AF=BE,
∵CE=EB=CB,
∴AF=AB,
∴AF=BF,
∴FA=FH,
∵FG⊥AH,
∴AG=GH,
∴DH=AD,
∵AT=DT=CE=BE,ATEC,
∴四边形AECT是平行四边形,
∴AECT,
∴CT⊥DF,
同法可证CD=CG,
∴DH=CG,
∴∠CDG=∠CGD,
∵∠CGE+∠CGD=90°,∠CDG+∠ADG=90°,
∴∠CGE=∠ADF=∠BAE,
∵∠AGI=∠CGE,
∴∠IAG=∠IGA,
∵∠DAH=∠DHA,∠GAI+∠DAG=90°,
∴∠CGE+∠AHD=90°,
∴∠GJH=90°,
∴DH⊥CG,故①正确,
∵∠IAG+∠AFG=90°,∠IGA+∠IGF=90°,
∴∠IFG=∠IFG,
∴IA=IG=IF=AF=AB,故②正确,
设BE=EC=m,则AB=BC=2m,AE=m,
过点H作HR⊥BC于点R,HW⊥CD于点W,
∵BH⊥AE,
∴,
∴,
同法,
∴,
∴,
∴,故③错误,
∵四边形HRCW是矩形,
∴,
∴,故④错误.
故选:B.
11‘平行四边形对边相等,周长为24cm,相邻两边长的比为3:1,则设邻边为
,
解得,
即这个平行四边形较短的边长为3cm,
故答案为:3.
12.∵为正三角形,∴,
∵菱形的两条对角线长分别为3cm和cm,∴菱形的边长为3cm,
∴AB=BC=AC=3×3=9(cm),
∴三角形的高(cm),
∴,
故答案为:.
13.可推出平行四边形ABCDABCD是矩形有②④,概率为.
14.
解:如图所示(画一个即可)
故答案为: 5或4.
15.∵四边形ABCB 是正方形,
∴AB=AB ,AB∥CB ,
∴AB∥A C,
∴∠CA A=30°,
∴A B =,AA =2,
∴A B =A B =,
∴A A =2,
同理:A A =2() ,
=2() ,
…
∴
∴
故答案为
16.∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
∵ M、N分别是OA,OC的中点
∴OM=ON
∴四边形BMDN是平行四边形.
17方法一:找出平行四边形的左右两条边的四等分点,依次对应连接起来,即可将平行四边形四等分;
方法二:连接平行四边形的两组对边的中点,即可把平行四边形四等分;
方法三:连接平行四边形的两条对角线,即可把平行四边形四等分;据此即可画图.
试题分析:如图所示:
18.
(1)
平移变换的性质分别作出A,B的对应点A′、B′,
如图,段A'B'即为所求:
(2)
如图所示,菱形ABCD即为所求,答案不唯一;
(3)
,
∴菱形ABCD的周长=.
