2023年中考数学复习模拟考试一(含答案)
文档属性
| 名称 | 2023年中考数学复习模拟考试一(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 899.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 12:29:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考摸拟考试一
一、单选题(共30分)
1.(本题3分)的绝对值是( )
A. B. C. D.2
2.(本题3分)某文化旅游节期间,几名同学包租一辆面包车前去游览,面包车的租金为180元,出发时又增加了两名同学,结果每个同学比原来少分摊了3元车费,设实际参加游览的同学共人,则所列方程为( )
A. B.
C. D.
3.(本题3分)如图, 是 的平分线,,,则 的度数是( )
A. B. C. D.
4.(本题3分)关于x的一元二次方程的一个根是0,则a的值为( )
A.1 B.-1 C.1或-1 D.0
5.(本题3分)如图,矩形中,,点P从点B出发,沿向终点D匀速运动,设点P走过的路程为x,的面积为S,能正确反映S与x之间函数关系的图象是( )
A. B. C. D.
6.(本题3分)如图,直线 , 相交于点 , 于点 ,,( )
A. B. C. D.
7.(本题3分)抛物线的顶点坐标是( )
A. B. C. D.
8.(本题3分)要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A. B.
C. D.
9.(本题3分)如图,正三角形ABC的边长为3+,在三角形中放入正方形DEMN和正方形EFPH,使得D、E、F在边AB上,点P、N分别在边CB、CA上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
A. B. C.3 D.
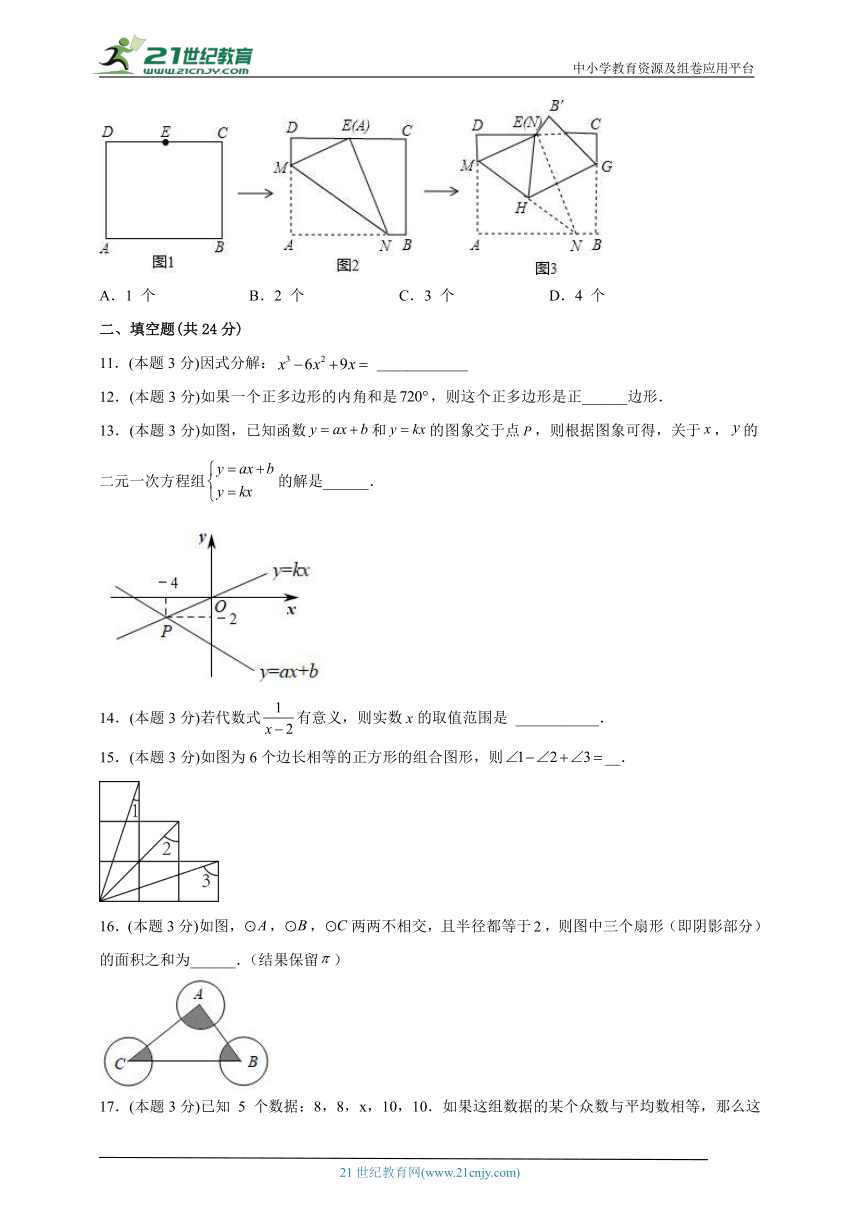
10.(本题3分)如图,在矩形 ABCD 中AB=8,AD=10,点 E 是 CD 的中点,将这张纸片依次折叠两次: 第一次折叠纸片使点 A 与点 E 重合,如图 2,折痕为 MN,连接 ME、NE;第二次折叠纸片使点 N 与点 E 重合,如图 3,点 B 落到 B′处,折痕为 HG,连接 HE,则下列结论正确的个数是( )①ME∥HG;②△MEH 是等边三角形;③∠EHG=∠AMN;④tan∠EHG=;
A.1 个 B.2 个 C.3 个 D.4 个
二、填空题(共24分)
11.(本题3分)因式分解: ____________
12.(本题3分)如果一个正多边形的内角和是,则这个正多边形是正______边形.
13.(本题3分)如图,已知函数和的图象交于点,则根据图象可得,关于,的二元一次方程组的解是______.
14.(本题3分)若代数式有意义,则实数x的取值范围是 ___________.
15.(本题3分)如图为6个边长相等的正方形的组合图形,则__.
16.(本题3分)如图,,,两两不相交,且半径都等于,则图中三个扇形(即阴影部分)的面积之和为______.(结果保留)
17.(本题3分)已知 5 个数据:8,8,x,10,10.如果这组数据的某个众数与平均数相等,那么这组数据的中位数是 __________.
18.(本题3分)如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
三、解答题(共46分)
19.(本题5分)如图,,,.求证:.
20.(本题5分)先化简,再求值:,其中.
21.(本题8分)小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去参加活动;将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新转动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.
22.(本题8分)如图,在中,,,垂足为点是外角的平分线,,垂足为点.
(1)求证:四边形为矩形;
(2)当满足什么条件时,四边形为正方形?给出证明.
23.(本题8分)某市,两个蔬菜基地得知黄岗,两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知蔬菜基地有蔬菜200t,蔬菜基地有蔬菜300t,现将这些蔬菜全部调运,两个灾区安置点,从地运往,两处的费用分别为每吨20元和25元,从地运往,两处的费用分别为每吨15元和18元.设从地运往处的蔬菜为吨.
(1)请填写下表,用含的代数式填空,结果要化简:
总计/
_________ _________ 200
_________ 300
总计/ 240 260 500
(2)设,两个蔬菜基地的总运费为元,求出与之间的函数关系式,并求总运费最小的调运方案;
(3)经过抢修,从地到处的路况得到进一步改善,缩短了运输时间,运费每吨减少元,其余线路的运费不变,试讨论总运费最小的调动方案.
24.(本题12分)如图,已知抛物线经过坐标原点和轴上另一点,顶点的坐标为.矩形的顶点与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形以每秒个单位长度的速度从图1所示的位置沿轴的正方向匀速平行移动,同时一动点也以相同的速度从点出发向匀速移动,设它们运动的时间为秒,直线与该抛物线的交点为(如图2所示).
①当,判断点是否在直线上,并说明理由;
②设P、N、C、D以为顶点的多边形面积为,试问是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
参考答案:
1.C
【分析】根据负数的绝对值是它的相反数进行求解即可.
【详解】解:的绝对值是,
故选:C.
【点睛】本题主要考查了求一个数的绝对值,熟知正数和0的绝对值是它本身,负数的绝对值是它的相反数是解题的关键.
2.A
【分析】设实际参加游览的同学共人,则原有的几名同学每人分担的车费为:元,出发时每名同学分担的车费为:,根据每个同学比原来少分摊了3元车费即可得到等量关系.
【详解】解:设实际参加游览的同学共人,
根据题意可得:,
故选:A.
【点睛】本题主要考查了分式方程的应用,解题的关键是首先弄清楚题意,根据关键描述语,找到合适的等量关系.
3.D
【分析】先根据角平分线求得,进而由邻补角求得,最后由三角形的外角性质即可求解.
【详解】解:∵是的平分线,,
∴,
∴,
∵,
∴,
故选D.
【点睛】本题主要考查了角平分线的有关计算、邻补角的有关计算以及三角形的外角性质,熟练掌握角平分线的定义以及外角性质是解题的关键.
4.B
【分析】根据一元二次方程解的定义得到,再解关于a的方程,然后根据一元二次方程定义确定a的值.
【详解】解:把代入一元二次方程得,
解得,
而,
的值为.
故选:B.
【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了一元二次方程的定义.
5.C
【分析】分当和两种情况讨论,分别求得函数关系式,即可判断.
【详解】解:由题意知,点P从点B出发,沿向终点D匀速运动,则
当时,,
当时,,
由以上分析可知,这个分段函数的图象开始是经过原点和点的一条线段,然后为经过点和点的一条水平线段.
故选:C.
【点睛】本题以动态的形式考查了分段函数,函数图象的知识和三角形面积,熟悉相关性质是解题的关键.
6.D
【分析】根据题意可以得到的度数,由,,从而可以得到的度数.
【详解】解:∵,
∴,
又∵,,
∴,
故选:D.
【点睛】本题考查垂线、平角,解题的关键是明确题意,找出所求问题需要的条件.
7.A
【分析】直接根据顶点式的特点写出顶点坐标.
【详解】解:∵为抛物线的顶点式,
∴根据顶点式的坐标特点可知,顶点坐标为,故A正确.
故选:A.
【点睛】本题考查了求抛物线的顶点坐标,掌握抛物线顶点式的特点是解题的关键.
8.B
【分析】先根据题意求出每支球队进行场比赛,再根据每个队之间比赛一场即可表示总的场次,然后根据总的比赛场次(场)列出方程即可.
【详解】根据题意可知.
故选:B.
【点睛】本题主要考查了一元二次方程的应用,确定等量关系是列方程的关键.
9.D
【分析】设正方形DEMN、正方形EFPH的边长分别为m、n,它们的面积和为S,根据等边三角形的性质得∠A=∠B=60°,利用含30度的直角三角形三边的关系得 ,,则 ,所以 , ,接着确定m的取值范围为: ,然后根据二次函数的性质求出S的最小值.
【详解】解:设正方形DEMN、正方形EFPH的边长分别为m、n,它们的面积和为S,
∵△ABC为等边三角形,
∴∠A=∠B=60°, ,
在Rt△ADN中,,
在Rt△BPF中,,
∵BD+DE+EF+CF=AB,
∴,
∴,
∴,
∴,
又∵当点M落在AC上,则正方形DEMN的边长最大,正方形EFPH的边长最小,
当点H落在BC上,则正方形DEMN的边长最小,正方形EFPH的边长最大,
∴当点M落在AC上时:
为正三角形,
在中,,,
∴ ,解得
在中,,
∵BD+DE+EF+CF=AB,
∴
解得,
∴,
∴当 时,S最小,S的最小值为 .
故选D.
【点睛】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;利用相似比计算相应线段的长.也考查了正方形的性质、等边三角形的性质和二次函数的性质.
10.C
【分析】根据折叠的性质可得M//GH,再根据等量代换,即可得出∠AMN=∠EHG;在直角三角形中运用勾股定理,即可得出AM=EM=7.4,再根据相似三角形的性质,即可得出EN=7、5=AN,进而得到,最后根据∠EMH≠60°,可得AMEH不是等边三角形.
【详解】
解:如图3,由折叠可得,∠MEN=∠A=90°,HG⊥NE,
即ME⊥EN,HG⊥EN,
∴EM//GH,故①正确;
∴∠NME=∠NHG,
由折叠可得,∠NME=∠AMV,∠EHG=∠NHG,
∴∠AMN=∠EHG,故③正确;
如图2,作NF⊥CD于F.
设DM=x,则AM=EM=10-x,
∵点E是CD的中点,AB=CD= ,
∴DE=CD=,
在Rt△DEM中,
∵
∴,解得x=2.6,
∴DM=2.6,AM=EM=7.4,
∵∠DEM+∠NEF=90°,∠NEF+∠ENH=90°,
∴∠DEM=∠ENF,
∵∠D=∠EFN=90°,
,
,
,故④正确;
又 ,
∴ ,即,
不是等边三角形,故②错误.
正确的结论有3个.
故选C.
【点睛】本题属于四边形综合题,主要考查翻折变换、勾股定理、相似三角形的判定和性质等知识的综合应用,解题的关键是作辅助线构造相似三角形,依据相似三角形对应边成比例,求得EN的长度.解决折叠问题时,常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.
11.
【分析】先提公因式x,然后利用公式法分解因式.
【详解】解:,
故答案为:.
【点睛】本题考查公因式法,公式法分解因式,掌握完全平方公式是解题的关键.
12.六
【分析】根据多边形的内角和公式求解即可.
【详解】设这个正多边形是正n边形,
则,
解得:.
∴这个正多边形是正六边形.
故答案为:六.
【点睛】本题考查多边形的内角和公式.掌握n边形的内角和为是解题关键.
13.
【分析】根据函数图象可以得到两个函数交点坐标,从而可以得到两个函数联立的二元一次方程组的解.
【详解】解:根据函数图可知:
函数和的图象交于点P的坐标是,
所以的解为,
故答案是:.
【点睛】本题主要考查一次函数与二元一次方程组,解题的关键是明确题意,利用数形结合的思想解答问题.
14.
【分析】根据分式的分母不能为零求解即可.
【详解】解:要使代数式有意义,只需,
∴,
则实数x的取值范围是,
故答案为:.
【点睛】本题考查分式有意义的条件,熟知分式有意义的条件是分母不为零是解答的关键.
15.##度
【分析】如图,利用“边角边”证明和全等,根据全等三角形对应角相等可得,然后求出,再判断出,然后计算即可得解.
【详解】解:标注字母,如图所示,
在和中,
,
∴(),
∴,
∵,
∴,
又∵,
∴.
故答案为:.
【点睛】本题考查了全等三角形的判定和性质,网格结构,准确识图并判断出全等三角形是解题的关键.
16.
【分析】根据三个扇形的半径都是,由扇形的面积公式即可求出阴影部分的面积.
【详解】解:三个扇形的半径都是,
而三个圆心角的和是,
图中的三个扇形即三个阴影部分的面积之和为.
故答案为:.
【点睛】考查了扇形面积的计算,因为三个扇形的半径相等,所以不需知道各个扇形的圆心角的度数,只需知道三个圆心角的和即可.
17.8 或 10
【分析】根据这组数据的某个众数与平均数相等,得出平均数等于8或10,求出x从而得出中位数,即是所求答案.
【详解】解:设众数是8,则由 ,解得:x=4,故中位数是8;
设众数是10,则由 ,解得:x=14,故中位数是10.
故答案为8或10.
【点睛】本题主要考查了众数的定义以及平均数的求法,还有中位数的确定方法,众数是两个需要分类讨论是解答本题的关键.
18.
【分析】根据矩形ABCD中,AB=3,BC=4,可得AC=5,由AE=可得点F是边BC上的任意位置时,点C始终在AC的下方,设点G到AC的距离为h,要使四边形AGCD的面积的最小,即h最小.所以点G在以点E为圆心,BE为半径的圆上,且在矩形ABCD的内部.过点E作EH⊥AC,交圆E于点G,此时h最小.根据锐角三角函数先求得h的值,再分别求得三角形ACD和三角形ACG的面积即可得结论.
【详解】解:如图,连接AC,
在矩形ABCD中,AB=3,BC=4,
∠B=∠D=90°,
∴AC=5,
∵AB=3,AE=,
∴点F是边BC上的任意位置时,点G始终在AC的下方,
设点G到AC的距离为h,
S四边形AGCD=S△ACD+S△ACG
=3×4+×5h,
=6+h.
要使四边形AGCD的面积的最小,即h最小.
∵点G在以点E为圆心,BE为半径的圆上,且在矩形ABCD的内部.
过点E作EH⊥AC,交圆E于点G,此时h最小.
在Rt△ABC中,sin∠BAC=,
在Rt△AEH中,AE=,
sin∠BAC=,
解得EH=AE=,
EG=BE=AB﹣AE=3﹣,
∴h=EH﹣EG=﹣(3﹣)=﹣3.
∴S四边形AGCD=6+×(﹣3)
=.
故答案为:.
【点睛】本题考查了翻折变换,解决本题的关键是确定满足条件的点G的位置,运用相似、锐角三角函数等知识解决问题.
19.见解析
【分析】由题意易得,,然后可证,进而问题可求解.
【详解】证明:∵,
∴,
∵,
∴,
即,
在和中,
,
∴(SAS),
∴,
∴.
【点睛】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
20.,
【分析】先将分式的分子、分母因式分解,再进行约分,然后进行分式的加减运算,再代值计算.
【详解】解:
,
当时,原式.
【点睛】本题考查了分式的化简求值.解答此题的关键是把分式化到最简,然后代值计算.
21.(1)
(2)不公平,理由见解析
【分析】(1)分别写出所有可能的结果和2的倍数的结果,然后根据概率公式即可计算出转到2的倍数的概率;
(2)根据题意,可得共有9种等可能的结果,然后再分别表示出2的倍数结果和3的倍数的结果,再利用概率公式计算出两人去参加活动的概率,再进行比较即可判断.
【详解】(1)解:∵共有1、2、3、4、5、6、7、8、9这9种等可能的结果,其中2的倍数有4个,分别是2、4、6、8,
∴P(转到2的倍数);
(2)解:游戏不公平,理由如下:
∵共有9种等可能的结果,其中2的倍数有2、4、6、8共4种可能,
∴P(转到2的倍数),
∴小亮去参加活动的概率为:,
又∵3的倍数有3、6、9共3种可能,
∴P(转到3的倍数),
∴小芳去参加活动的概率为:,
∵,
∴游戏不公平.
【点睛】本题考查了频率与概率,解本题的关键在正确找出所有可能的结果.概率公式等于所求情况数与总情况数之比.
22.(1)证明见解析;
(2)当满足时,四边形是一个正方形,证明见解析
【分析】(1)根据等腰三角形的性质得出,根据是外角的平分线,得出,进而得出,根据,得出,根据矩形的判定定理即可判定四边形为矩形;
(2)根据题意证明可得四边形为正方形,继而可得当满足,即可求解.
【详解】(1)证明:在中,,
∴,
∵是外角的平分线,
∴,
∴,
又∵,
∴,
∴四边形为矩形.
(2)当满足时,四边形是一个正方形.
理由:∵,
∴,
∵,
∴,
∴,
∵四边形为矩形,
∴矩形是正方形.
∴当时,四边形ADCE是一个正方形.
【点睛】本题考查了矩形的判定,等腰三角形的性质,正方形的判定,综合运用以上知识是解题的关键.
23.(1),,;(2);A→C:200吨,A→D: 0吨,B→C:40吨,B→D:260吨;(3)时,在的前提下调运方案的总费用不变; 时,总费用最小,其调运方案为:A→C:0吨,A→D: 200吨,B→C:240吨,B→D:60吨;
【分析】(1)根据题意,从A处调运到C处的数量为(240-x)t;从A处调往D处的数量为[200-(240-x)]t;则从B调运到D处的数量为(300-x)t;
(2)根据调运总费用等于四种调运单价乘以对应的吨数的积的和,易得w与x的函数关系,根据调运的数量非负即可不等式组,求得x的范围,从而可求得总费用的最小的调运方案;
(3)由题意可得w与x的关系式,根据x的取值范围不同而有不同的解,分情况讨论:当0【详解】(1)填表如下:
总计/
200
300
总计/ 240 260 500
故答案为:,,;
(2)与之间的函数关系为:
由题意得:
∴
∵在中,
∴随的增大而增大
∴当时,总运费最小
此时调运方案为:
200吨 0吨
40吨 260吨
(3)由题意得
即,其中
∴,(2)中调运方案总费用最小;
时,在的前提下调运方案的总费用不变;
时,总费用最小,其调运方案如下:
0吨 200吨
240吨 60吨
【点睛】本题是一次函数在实际问题中的应用,具有较强的综合性与较大的难度.它考查了一次函数的性质,求一次函数的解析式,解一元一次方程组等知识,用到分类讨论思想.
24.(1)y=-x2+4x;(2)点P不在直线MB上,理由见解析;②当t=时,以点P,N,C,D为顶点的多边形面积有最大值,这个最大值为.
【分析】(1)设抛物线解析式为,将代入求出即可解决问题;
(2)①由(1)中抛物线的解析式可以求出点的坐标,从而可以求出的解析式,再将点的坐标代入直线的解析式就可以判断点是否在直线上.
②设出点,,可以表示出的值,根据梯形的面积公式可以表示出与的函数关系式,从而可以求出结论.
【详解】解:(1)设抛物线解析式为,
把代入解析式得,
解得,,
函数解析式为,即.
(2)①,
当时,,
,,
,
设直线的解析式为:,则
,
解得:,
直线的解析式为:,
当时,,,
当时,,
当时,点不在直线上.
②存在最大值.理由如下:
点在轴的非负半轴上,且在抛物线上,
.
点,的坐标分别为、,
,
,
,
I.当,即或时,以点,,,为顶点的多边形是三角形,此三角形的高为,
,
II.当时,以点,,,为顶点的多边形是四边形,
,,
,
,
,
,
时,有最大值为,
综合以上可得,当时,以点,,,为顶点的多边形面积有最大值,这个最大值为.
【点睛】此题主要考查了待定系数法求函数的解析式,二次函数的最值,二次函数图象上点的坐标特征,三角形的面积公式的运用,梯形的面积公式的运用.根据几何关系巧妙设点,把面积用表示出来,转化为函数最值问题是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考摸拟考试一
一、单选题(共30分)
1.(本题3分)的绝对值是( )
A. B. C. D.2
2.(本题3分)某文化旅游节期间,几名同学包租一辆面包车前去游览,面包车的租金为180元,出发时又增加了两名同学,结果每个同学比原来少分摊了3元车费,设实际参加游览的同学共人,则所列方程为( )
A. B.
C. D.
3.(本题3分)如图, 是 的平分线,,,则 的度数是( )
A. B. C. D.
4.(本题3分)关于x的一元二次方程的一个根是0,则a的值为( )
A.1 B.-1 C.1或-1 D.0
5.(本题3分)如图,矩形中,,点P从点B出发,沿向终点D匀速运动,设点P走过的路程为x,的面积为S,能正确反映S与x之间函数关系的图象是( )
A. B. C. D.
6.(本题3分)如图,直线 , 相交于点 , 于点 ,,( )
A. B. C. D.
7.(本题3分)抛物线的顶点坐标是( )
A. B. C. D.
8.(本题3分)要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A. B.
C. D.
9.(本题3分)如图,正三角形ABC的边长为3+,在三角形中放入正方形DEMN和正方形EFPH,使得D、E、F在边AB上,点P、N分别在边CB、CA上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
A. B. C.3 D.
10.(本题3分)如图,在矩形 ABCD 中AB=8,AD=10,点 E 是 CD 的中点,将这张纸片依次折叠两次: 第一次折叠纸片使点 A 与点 E 重合,如图 2,折痕为 MN,连接 ME、NE;第二次折叠纸片使点 N 与点 E 重合,如图 3,点 B 落到 B′处,折痕为 HG,连接 HE,则下列结论正确的个数是( )①ME∥HG;②△MEH 是等边三角形;③∠EHG=∠AMN;④tan∠EHG=;
A.1 个 B.2 个 C.3 个 D.4 个
二、填空题(共24分)
11.(本题3分)因式分解: ____________
12.(本题3分)如果一个正多边形的内角和是,则这个正多边形是正______边形.
13.(本题3分)如图,已知函数和的图象交于点,则根据图象可得,关于,的二元一次方程组的解是______.
14.(本题3分)若代数式有意义,则实数x的取值范围是 ___________.
15.(本题3分)如图为6个边长相等的正方形的组合图形,则__.
16.(本题3分)如图,,,两两不相交,且半径都等于,则图中三个扇形(即阴影部分)的面积之和为______.(结果保留)
17.(本题3分)已知 5 个数据:8,8,x,10,10.如果这组数据的某个众数与平均数相等,那么这组数据的中位数是 __________.
18.(本题3分)如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
三、解答题(共46分)
19.(本题5分)如图,,,.求证:.
20.(本题5分)先化简,再求值:,其中.
21.(本题8分)小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去参加活动;将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新转动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.
22.(本题8分)如图,在中,,,垂足为点是外角的平分线,,垂足为点.
(1)求证:四边形为矩形;
(2)当满足什么条件时,四边形为正方形?给出证明.
23.(本题8分)某市,两个蔬菜基地得知黄岗,两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知蔬菜基地有蔬菜200t,蔬菜基地有蔬菜300t,现将这些蔬菜全部调运,两个灾区安置点,从地运往,两处的费用分别为每吨20元和25元,从地运往,两处的费用分别为每吨15元和18元.设从地运往处的蔬菜为吨.
(1)请填写下表,用含的代数式填空,结果要化简:
总计/
_________ _________ 200
_________ 300
总计/ 240 260 500
(2)设,两个蔬菜基地的总运费为元,求出与之间的函数关系式,并求总运费最小的调运方案;
(3)经过抢修,从地到处的路况得到进一步改善,缩短了运输时间,运费每吨减少元,其余线路的运费不变,试讨论总运费最小的调动方案.
24.(本题12分)如图,已知抛物线经过坐标原点和轴上另一点,顶点的坐标为.矩形的顶点与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形以每秒个单位长度的速度从图1所示的位置沿轴的正方向匀速平行移动,同时一动点也以相同的速度从点出发向匀速移动,设它们运动的时间为秒,直线与该抛物线的交点为(如图2所示).
①当,判断点是否在直线上,并说明理由;
②设P、N、C、D以为顶点的多边形面积为,试问是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
参考答案:
1.C
【分析】根据负数的绝对值是它的相反数进行求解即可.
【详解】解:的绝对值是,
故选:C.
【点睛】本题主要考查了求一个数的绝对值,熟知正数和0的绝对值是它本身,负数的绝对值是它的相反数是解题的关键.
2.A
【分析】设实际参加游览的同学共人,则原有的几名同学每人分担的车费为:元,出发时每名同学分担的车费为:,根据每个同学比原来少分摊了3元车费即可得到等量关系.
【详解】解:设实际参加游览的同学共人,
根据题意可得:,
故选:A.
【点睛】本题主要考查了分式方程的应用,解题的关键是首先弄清楚题意,根据关键描述语,找到合适的等量关系.
3.D
【分析】先根据角平分线求得,进而由邻补角求得,最后由三角形的外角性质即可求解.
【详解】解:∵是的平分线,,
∴,
∴,
∵,
∴,
故选D.
【点睛】本题主要考查了角平分线的有关计算、邻补角的有关计算以及三角形的外角性质,熟练掌握角平分线的定义以及外角性质是解题的关键.
4.B
【分析】根据一元二次方程解的定义得到,再解关于a的方程,然后根据一元二次方程定义确定a的值.
【详解】解:把代入一元二次方程得,
解得,
而,
的值为.
故选:B.
【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了一元二次方程的定义.
5.C
【分析】分当和两种情况讨论,分别求得函数关系式,即可判断.
【详解】解:由题意知,点P从点B出发,沿向终点D匀速运动,则
当时,,
当时,,
由以上分析可知,这个分段函数的图象开始是经过原点和点的一条线段,然后为经过点和点的一条水平线段.
故选:C.
【点睛】本题以动态的形式考查了分段函数,函数图象的知识和三角形面积,熟悉相关性质是解题的关键.
6.D
【分析】根据题意可以得到的度数,由,,从而可以得到的度数.
【详解】解:∵,
∴,
又∵,,
∴,
故选:D.
【点睛】本题考查垂线、平角,解题的关键是明确题意,找出所求问题需要的条件.
7.A
【分析】直接根据顶点式的特点写出顶点坐标.
【详解】解:∵为抛物线的顶点式,
∴根据顶点式的坐标特点可知,顶点坐标为,故A正确.
故选:A.
【点睛】本题考查了求抛物线的顶点坐标,掌握抛物线顶点式的特点是解题的关键.
8.B
【分析】先根据题意求出每支球队进行场比赛,再根据每个队之间比赛一场即可表示总的场次,然后根据总的比赛场次(场)列出方程即可.
【详解】根据题意可知.
故选:B.
【点睛】本题主要考查了一元二次方程的应用,确定等量关系是列方程的关键.
9.D
【分析】设正方形DEMN、正方形EFPH的边长分别为m、n,它们的面积和为S,根据等边三角形的性质得∠A=∠B=60°,利用含30度的直角三角形三边的关系得 ,,则 ,所以 , ,接着确定m的取值范围为: ,然后根据二次函数的性质求出S的最小值.
【详解】解:设正方形DEMN、正方形EFPH的边长分别为m、n,它们的面积和为S,
∵△ABC为等边三角形,
∴∠A=∠B=60°, ,
在Rt△ADN中,,
在Rt△BPF中,,
∵BD+DE+EF+CF=AB,
∴,
∴,
∴,
∴,
又∵当点M落在AC上,则正方形DEMN的边长最大,正方形EFPH的边长最小,
当点H落在BC上,则正方形DEMN的边长最小,正方形EFPH的边长最大,
∴当点M落在AC上时:
为正三角形,
在中,,,
∴ ,解得
在中,,
∵BD+DE+EF+CF=AB,
∴
解得,
∴,
∴当 时,S最小,S的最小值为 .
故选D.
【点睛】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;利用相似比计算相应线段的长.也考查了正方形的性质、等边三角形的性质和二次函数的性质.
10.C
【分析】根据折叠的性质可得M//GH,再根据等量代换,即可得出∠AMN=∠EHG;在直角三角形中运用勾股定理,即可得出AM=EM=7.4,再根据相似三角形的性质,即可得出EN=7、5=AN,进而得到,最后根据∠EMH≠60°,可得AMEH不是等边三角形.
【详解】
解:如图3,由折叠可得,∠MEN=∠A=90°,HG⊥NE,
即ME⊥EN,HG⊥EN,
∴EM//GH,故①正确;
∴∠NME=∠NHG,
由折叠可得,∠NME=∠AMV,∠EHG=∠NHG,
∴∠AMN=∠EHG,故③正确;
如图2,作NF⊥CD于F.
设DM=x,则AM=EM=10-x,
∵点E是CD的中点,AB=CD= ,
∴DE=CD=,
在Rt△DEM中,
∵
∴,解得x=2.6,
∴DM=2.6,AM=EM=7.4,
∵∠DEM+∠NEF=90°,∠NEF+∠ENH=90°,
∴∠DEM=∠ENF,
∵∠D=∠EFN=90°,
,
,
,故④正确;
又 ,
∴ ,即,
不是等边三角形,故②错误.
正确的结论有3个.
故选C.
【点睛】本题属于四边形综合题,主要考查翻折变换、勾股定理、相似三角形的判定和性质等知识的综合应用,解题的关键是作辅助线构造相似三角形,依据相似三角形对应边成比例,求得EN的长度.解决折叠问题时,常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.
11.
【分析】先提公因式x,然后利用公式法分解因式.
【详解】解:,
故答案为:.
【点睛】本题考查公因式法,公式法分解因式,掌握完全平方公式是解题的关键.
12.六
【分析】根据多边形的内角和公式求解即可.
【详解】设这个正多边形是正n边形,
则,
解得:.
∴这个正多边形是正六边形.
故答案为:六.
【点睛】本题考查多边形的内角和公式.掌握n边形的内角和为是解题关键.
13.
【分析】根据函数图象可以得到两个函数交点坐标,从而可以得到两个函数联立的二元一次方程组的解.
【详解】解:根据函数图可知:
函数和的图象交于点P的坐标是,
所以的解为,
故答案是:.
【点睛】本题主要考查一次函数与二元一次方程组,解题的关键是明确题意,利用数形结合的思想解答问题.
14.
【分析】根据分式的分母不能为零求解即可.
【详解】解:要使代数式有意义,只需,
∴,
则实数x的取值范围是,
故答案为:.
【点睛】本题考查分式有意义的条件,熟知分式有意义的条件是分母不为零是解答的关键.
15.##度
【分析】如图,利用“边角边”证明和全等,根据全等三角形对应角相等可得,然后求出,再判断出,然后计算即可得解.
【详解】解:标注字母,如图所示,
在和中,
,
∴(),
∴,
∵,
∴,
又∵,
∴.
故答案为:.
【点睛】本题考查了全等三角形的判定和性质,网格结构,准确识图并判断出全等三角形是解题的关键.
16.
【分析】根据三个扇形的半径都是,由扇形的面积公式即可求出阴影部分的面积.
【详解】解:三个扇形的半径都是,
而三个圆心角的和是,
图中的三个扇形即三个阴影部分的面积之和为.
故答案为:.
【点睛】考查了扇形面积的计算,因为三个扇形的半径相等,所以不需知道各个扇形的圆心角的度数,只需知道三个圆心角的和即可.
17.8 或 10
【分析】根据这组数据的某个众数与平均数相等,得出平均数等于8或10,求出x从而得出中位数,即是所求答案.
【详解】解:设众数是8,则由 ,解得:x=4,故中位数是8;
设众数是10,则由 ,解得:x=14,故中位数是10.
故答案为8或10.
【点睛】本题主要考查了众数的定义以及平均数的求法,还有中位数的确定方法,众数是两个需要分类讨论是解答本题的关键.
18.
【分析】根据矩形ABCD中,AB=3,BC=4,可得AC=5,由AE=可得点F是边BC上的任意位置时,点C始终在AC的下方,设点G到AC的距离为h,要使四边形AGCD的面积的最小,即h最小.所以点G在以点E为圆心,BE为半径的圆上,且在矩形ABCD的内部.过点E作EH⊥AC,交圆E于点G,此时h最小.根据锐角三角函数先求得h的值,再分别求得三角形ACD和三角形ACG的面积即可得结论.
【详解】解:如图,连接AC,
在矩形ABCD中,AB=3,BC=4,
∠B=∠D=90°,
∴AC=5,
∵AB=3,AE=,
∴点F是边BC上的任意位置时,点G始终在AC的下方,
设点G到AC的距离为h,
S四边形AGCD=S△ACD+S△ACG
=3×4+×5h,
=6+h.
要使四边形AGCD的面积的最小,即h最小.
∵点G在以点E为圆心,BE为半径的圆上,且在矩形ABCD的内部.
过点E作EH⊥AC,交圆E于点G,此时h最小.
在Rt△ABC中,sin∠BAC=,
在Rt△AEH中,AE=,
sin∠BAC=,
解得EH=AE=,
EG=BE=AB﹣AE=3﹣,
∴h=EH﹣EG=﹣(3﹣)=﹣3.
∴S四边形AGCD=6+×(﹣3)
=.
故答案为:.
【点睛】本题考查了翻折变换,解决本题的关键是确定满足条件的点G的位置,运用相似、锐角三角函数等知识解决问题.
19.见解析
【分析】由题意易得,,然后可证,进而问题可求解.
【详解】证明:∵,
∴,
∵,
∴,
即,
在和中,
,
∴(SAS),
∴,
∴.
【点睛】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
20.,
【分析】先将分式的分子、分母因式分解,再进行约分,然后进行分式的加减运算,再代值计算.
【详解】解:
,
当时,原式.
【点睛】本题考查了分式的化简求值.解答此题的关键是把分式化到最简,然后代值计算.
21.(1)
(2)不公平,理由见解析
【分析】(1)分别写出所有可能的结果和2的倍数的结果,然后根据概率公式即可计算出转到2的倍数的概率;
(2)根据题意,可得共有9种等可能的结果,然后再分别表示出2的倍数结果和3的倍数的结果,再利用概率公式计算出两人去参加活动的概率,再进行比较即可判断.
【详解】(1)解:∵共有1、2、3、4、5、6、7、8、9这9种等可能的结果,其中2的倍数有4个,分别是2、4、6、8,
∴P(转到2的倍数);
(2)解:游戏不公平,理由如下:
∵共有9种等可能的结果,其中2的倍数有2、4、6、8共4种可能,
∴P(转到2的倍数),
∴小亮去参加活动的概率为:,
又∵3的倍数有3、6、9共3种可能,
∴P(转到3的倍数),
∴小芳去参加活动的概率为:,
∵,
∴游戏不公平.
【点睛】本题考查了频率与概率,解本题的关键在正确找出所有可能的结果.概率公式等于所求情况数与总情况数之比.
22.(1)证明见解析;
(2)当满足时,四边形是一个正方形,证明见解析
【分析】(1)根据等腰三角形的性质得出,根据是外角的平分线,得出,进而得出,根据,得出,根据矩形的判定定理即可判定四边形为矩形;
(2)根据题意证明可得四边形为正方形,继而可得当满足,即可求解.
【详解】(1)证明:在中,,
∴,
∵是外角的平分线,
∴,
∴,
又∵,
∴,
∴四边形为矩形.
(2)当满足时,四边形是一个正方形.
理由:∵,
∴,
∵,
∴,
∴,
∵四边形为矩形,
∴矩形是正方形.
∴当时,四边形ADCE是一个正方形.
【点睛】本题考查了矩形的判定,等腰三角形的性质,正方形的判定,综合运用以上知识是解题的关键.
23.(1),,;(2);A→C:200吨,A→D: 0吨,B→C:40吨,B→D:260吨;(3)时,在的前提下调运方案的总费用不变; 时,总费用最小,其调运方案为:A→C:0吨,A→D: 200吨,B→C:240吨,B→D:60吨;
【分析】(1)根据题意,从A处调运到C处的数量为(240-x)t;从A处调往D处的数量为[200-(240-x)]t;则从B调运到D处的数量为(300-x)t;
(2)根据调运总费用等于四种调运单价乘以对应的吨数的积的和,易得w与x的函数关系,根据调运的数量非负即可不等式组,求得x的范围,从而可求得总费用的最小的调运方案;
(3)由题意可得w与x的关系式,根据x的取值范围不同而有不同的解,分情况讨论:当0
总计/
200
300
总计/ 240 260 500
故答案为:,,;
(2)与之间的函数关系为:
由题意得:
∴
∵在中,
∴随的增大而增大
∴当时,总运费最小
此时调运方案为:
200吨 0吨
40吨 260吨
(3)由题意得
即,其中
∴,(2)中调运方案总费用最小;
时,在的前提下调运方案的总费用不变;
时,总费用最小,其调运方案如下:
0吨 200吨
240吨 60吨
【点睛】本题是一次函数在实际问题中的应用,具有较强的综合性与较大的难度.它考查了一次函数的性质,求一次函数的解析式,解一元一次方程组等知识,用到分类讨论思想.
24.(1)y=-x2+4x;(2)点P不在直线MB上,理由见解析;②当t=时,以点P,N,C,D为顶点的多边形面积有最大值,这个最大值为.
【分析】(1)设抛物线解析式为,将代入求出即可解决问题;
(2)①由(1)中抛物线的解析式可以求出点的坐标,从而可以求出的解析式,再将点的坐标代入直线的解析式就可以判断点是否在直线上.
②设出点,,可以表示出的值,根据梯形的面积公式可以表示出与的函数关系式,从而可以求出结论.
【详解】解:(1)设抛物线解析式为,
把代入解析式得,
解得,,
函数解析式为,即.
(2)①,
当时,,
,,
,
设直线的解析式为:,则
,
解得:,
直线的解析式为:,
当时,,,
当时,,
当时,点不在直线上.
②存在最大值.理由如下:
点在轴的非负半轴上,且在抛物线上,
.
点,的坐标分别为、,
,
,
,
I.当,即或时,以点,,,为顶点的多边形是三角形,此三角形的高为,
,
II.当时,以点,,,为顶点的多边形是四边形,
,,
,
,
,
,
时,有最大值为,
综合以上可得,当时,以点,,,为顶点的多边形面积有最大值,这个最大值为.
【点睛】此题主要考查了待定系数法求函数的解析式,二次函数的最值,二次函数图象上点的坐标特征,三角形的面积公式的运用,梯形的面积公式的运用.根据几何关系巧妙设点,把面积用表示出来,转化为函数最值问题是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
