人教版数学八年级下册18.2.1矩形的性质 课件(共27张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.2.1矩形的性质 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 23:16:06 | ||
图片预览






文档简介
(共27张PPT)
18.2特殊的平行四边形
18.2.1 矩形的性质
人教版九年义务教育八年级下册
学习目标
1.理解矩形的概念,明确矩形与平行四边形之间的关系.
2.探索、猜想并能够证明矩形的性质定理.
3.掌握矩形的性质,能根据矩形的性质解决简单的实际问题.
4.理解直角三角形斜边上的中线等于斜边的一半.
温故知新
A
B
D
C
1.什么是平行四边形?
2.平行四边形有哪些性质?
概念:两组对边分别平行的四边形是平行四边形.
性质:边:对边平行且相等.
角:对角相等.
对角线:对角线互相平分.
对称性:中心对称图形,对称中心是对角线的交点.
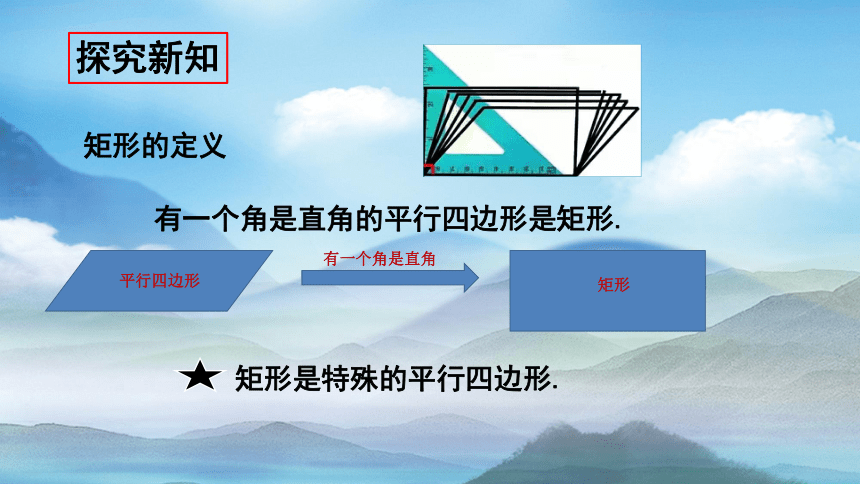
探究新知
有一个角是直角的平行四边形是矩形.
矩形是特殊的平行四边形.
平行四边形
矩形
有一个角是直角
矩形的定义
生活中的矩形
中国国旗
香港区旗
窗框
课本封面
桌椅面
电视机面
A
D
A
B
C
D
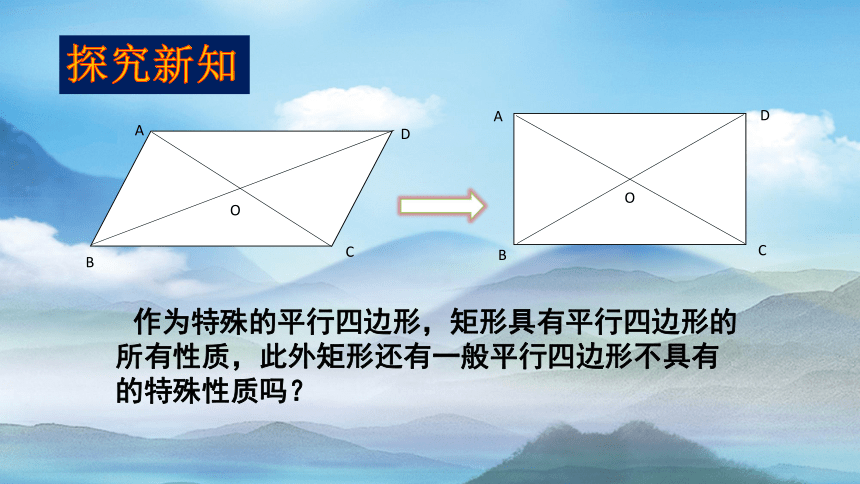
作为特殊的平行四边形,矩形具有平行四边形的
所有性质,此外矩形还有一般平行四边形不具有的特殊性质吗?
探究新知
B
C
O
O
动手操作
请你利用手中的矩形卡片,在四个角标上字母,配合量角器和直尺,测量它的四个角的度数和对角线的长度,类比平行四边形的性质的探究过程,从边、角、对角线的角度进行思考,讨论、交流、得出初步猜想并归纳整理成文字表述.
类比探究
探究新知
矩形是一个特殊的平行四边形,角除了对角相等,邻角互补
还有哪些特殊性质呢?
猜想一:矩形的四个角都是直角
A
B
C
D
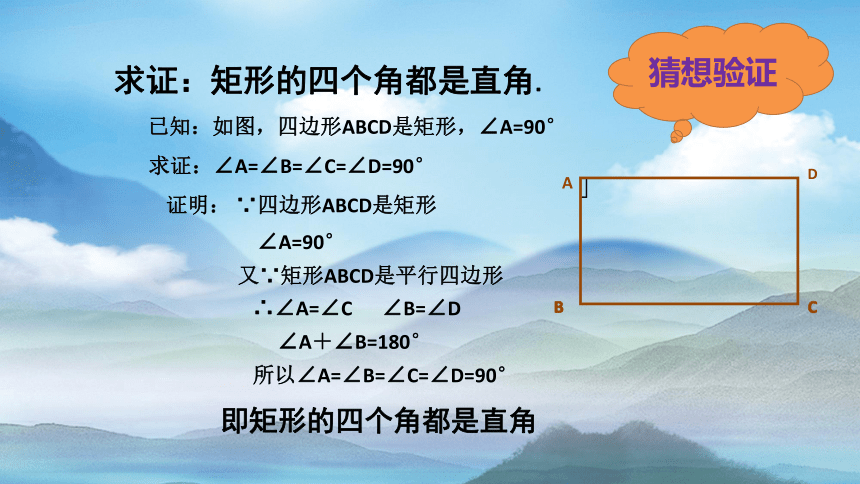
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,∠A=90°
求证:∠A=∠B=∠C=∠D=90°
证明: ∵四边形ABCD是矩形
又∵矩形ABCD是平行四边形
∠A=90°
∴∠A=∠C ∠B=∠D
∠A+∠B=180°
所以∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
A
B
C
D
猜想验证
」
探究新知
矩形是一个特殊的平行四边形,对角线除了互相
平分外还有哪些特殊性质呢?
猜想二:矩形的对角线相等.
A
B
C
D
O
求证:矩形的对角线相等.
已知:如图,四边形ABCD是矩形,
∠ABC=90°
求证:AC=BD
证明:∵四边形ABCD是矩形
∴∠ABC=∠DCB=90°
又∵AB=DC, BC=CB
∴▲ABC≌▲DCB
∴AC=BD 即矩形的对角线相等
A
B
C
D
猜想验证
﹁
O
矩形的特殊性质一:矩形的四个角都是直角.
几何语言;∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
矩形的特殊性质二:矩形的对角线相等.
几何语言:∵四边形ABCD是矩形
∴AC=BD
A
B
C
D
A
B
C
D
折一折
平行四边形是轴对称图形吗?
矩形是轴对称图形吗?
矩形是轴对称图形,一共有两条对称轴.
试试看
请你抢答
1.矩形的定义中有两个条件:
一是:
有一个角是直角
二是:
是一个平行四边形
跟踪训练
请你抢答
2.矩形具有而平行四边形不一定具有的性质
是 ___________________(填代号)
(1)对边平行且相等;
(2)对角线相等;
(3)对角相等;
(4)对角线互相平分;
(5)4个角都是90°;
(6)轴对称图形.
(2)(5)(6)
生活链接-投圈游戏
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
公平,因为OA=OB=OC=OD
A
B
C
D
比一比 知关系
角 对角线 对称性
平行四边形 对边平行且相等 对角相等邻角互补 对角线互相平分 中心对称图形
矩形 对边平行且相等 四个角都是直角 对角线互相平分且相等 中性心对称图形轴对称图形
边
这是矩形所特有的性质
找找看 你能行
如图,在矩形ABCD中,AC与BD相交于点O,找出相等的线段,等腰三角形,直角三角形.
A
B
C
D
O
小试牛刀
探究新知
在直角三角形ABC中,O是AC的中点,
进而思考BO与AC的数量关系.
A
B
C
D
O
根据矩形的性质可以得到:
OB=1/2 BD=1/2 AC
几何语言:
∵在直角三角形ABC中,BO是斜边AC上的中线
∴BO=1/2AC
A
B
C
O
推论:直角三角形斜边上的中线等于斜边的一半.
思考 如图,矩形ABCD的对角线AC和BD相交于点O。观察
学以致用
已知Rt▲ABC中,∠ABC=90°
BD是斜边AC上的中线.
(1)若BD=3cm 则AC=________cm
(2)若∠C=30°,AB=5cm,则AC=__________cm
BD=_____cm
A
B
C
D
6
10
5
例1:
如图,矩形ABCD的两条对角线相交于点O,
∠AOB=60°,AB=4CM,求矩形对角线的长是多少?
解:∵四边形ABCD是矩形
∴AC=BD AC=2AO BD=2BO
∴OA=OB
又∵∠AOB=60° AB=4cm
∴▲AOB是等边三角形
∴OA=AB=4cm
∴AC=BD=2 OA=8cm
A
B
C
D
O
应用新知 解决问题
(
变式:
如图,矩形ABCD的两条对角线相交于点O,已知∠BOC=120°,AB=6cm。求AC的长.
方法小结:如果矩形两对角线的夹角是60度或120度,
则其中必有等边三角形
A
B
C
D
O
矩形对角线
等边三角形
转化
60 °
能力提升
如图,将矩形ABCD沿着直线BD折叠,使点C落
在C’处,BC’交AD于点E,AD=8,AB=4,求三角形
BED的面积.
A
B
C
D
C’
1
2
3
E
解: ∵四边形ABCD是矩形
∴AD//BC,∠A=90° ∠2=∠3
又由折叠知∠1=∠2
∴∠1=∠3
∴BE=DE
设BE=DE=X,则AE=8-X
∵在Rt△ABE中,AB +AE =BE
∴4 +(8-X) =X
解得X=5,即DE=5
∴S△BED=1/2 DE ×AB=1/2×5×4=10
方法点拨 : 矩形的折叠问题常与勾股定理结合考察.
矩形的定义:
边
角
对角线
矩形对边平行且相等
矩形的四个角都是直角
矩形的对角线相等且互相平分
直角三角形斜边上的中线性质:
直角三角形斜边上的中线等于斜边的一半.
A
B
C
D
A
B
C
D
课堂小结
我的收获
1.知识:
有一个角是直角的平行四边形是矩形.
矩形的性质:
2.方法:类比探究
3.数学思想方法:
平行四边形 矩形
矩形
(特殊)
(一般)
直角三角形
等腰三角形
计算中找到等量关系,和勾股定理相结合,体现了数学学习中的转化和方程思想.
布置作业
必做:教材60页 3,4 题 61页8,9题.
选做:数学同步练习册47-48页.
18.2特殊的平行四边形
18.2.1 矩形的性质
人教版九年义务教育八年级下册
学习目标
1.理解矩形的概念,明确矩形与平行四边形之间的关系.
2.探索、猜想并能够证明矩形的性质定理.
3.掌握矩形的性质,能根据矩形的性质解决简单的实际问题.
4.理解直角三角形斜边上的中线等于斜边的一半.
温故知新
A
B
D
C
1.什么是平行四边形?
2.平行四边形有哪些性质?
概念:两组对边分别平行的四边形是平行四边形.
性质:边:对边平行且相等.
角:对角相等.
对角线:对角线互相平分.
对称性:中心对称图形,对称中心是对角线的交点.
探究新知
有一个角是直角的平行四边形是矩形.
矩形是特殊的平行四边形.
平行四边形
矩形
有一个角是直角
矩形的定义
生活中的矩形
中国国旗
香港区旗
窗框
课本封面
桌椅面
电视机面
A
D
A
B
C
D
作为特殊的平行四边形,矩形具有平行四边形的
所有性质,此外矩形还有一般平行四边形不具有的特殊性质吗?
探究新知
B
C
O
O
动手操作
请你利用手中的矩形卡片,在四个角标上字母,配合量角器和直尺,测量它的四个角的度数和对角线的长度,类比平行四边形的性质的探究过程,从边、角、对角线的角度进行思考,讨论、交流、得出初步猜想并归纳整理成文字表述.
类比探究
探究新知
矩形是一个特殊的平行四边形,角除了对角相等,邻角互补
还有哪些特殊性质呢?
猜想一:矩形的四个角都是直角
A
B
C
D
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,∠A=90°
求证:∠A=∠B=∠C=∠D=90°
证明: ∵四边形ABCD是矩形
又∵矩形ABCD是平行四边形
∠A=90°
∴∠A=∠C ∠B=∠D
∠A+∠B=180°
所以∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
A
B
C
D
猜想验证
」
探究新知
矩形是一个特殊的平行四边形,对角线除了互相
平分外还有哪些特殊性质呢?
猜想二:矩形的对角线相等.
A
B
C
D
O
求证:矩形的对角线相等.
已知:如图,四边形ABCD是矩形,
∠ABC=90°
求证:AC=BD
证明:∵四边形ABCD是矩形
∴∠ABC=∠DCB=90°
又∵AB=DC, BC=CB
∴▲ABC≌▲DCB
∴AC=BD 即矩形的对角线相等
A
B
C
D
猜想验证
﹁
O
矩形的特殊性质一:矩形的四个角都是直角.
几何语言;∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
矩形的特殊性质二:矩形的对角线相等.
几何语言:∵四边形ABCD是矩形
∴AC=BD
A
B
C
D
A
B
C
D
折一折
平行四边形是轴对称图形吗?
矩形是轴对称图形吗?
矩形是轴对称图形,一共有两条对称轴.
试试看
请你抢答
1.矩形的定义中有两个条件:
一是:
有一个角是直角
二是:
是一个平行四边形
跟踪训练
请你抢答
2.矩形具有而平行四边形不一定具有的性质
是 ___________________(填代号)
(1)对边平行且相等;
(2)对角线相等;
(3)对角相等;
(4)对角线互相平分;
(5)4个角都是90°;
(6)轴对称图形.
(2)(5)(6)
生活链接-投圈游戏
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
公平,因为OA=OB=OC=OD
A
B
C
D
比一比 知关系
角 对角线 对称性
平行四边形 对边平行且相等 对角相等邻角互补 对角线互相平分 中心对称图形
矩形 对边平行且相等 四个角都是直角 对角线互相平分且相等 中性心对称图形轴对称图形
边
这是矩形所特有的性质
找找看 你能行
如图,在矩形ABCD中,AC与BD相交于点O,找出相等的线段,等腰三角形,直角三角形.
A
B
C
D
O
小试牛刀
探究新知
在直角三角形ABC中,O是AC的中点,
进而思考BO与AC的数量关系.
A
B
C
D
O
根据矩形的性质可以得到:
OB=1/2 BD=1/2 AC
几何语言:
∵在直角三角形ABC中,BO是斜边AC上的中线
∴BO=1/2AC
A
B
C
O
推论:直角三角形斜边上的中线等于斜边的一半.
思考 如图,矩形ABCD的对角线AC和BD相交于点O。观察
学以致用
已知Rt▲ABC中,∠ABC=90°
BD是斜边AC上的中线.
(1)若BD=3cm 则AC=________cm
(2)若∠C=30°,AB=5cm,则AC=__________cm
BD=_____cm
A
B
C
D
6
10
5
例1:
如图,矩形ABCD的两条对角线相交于点O,
∠AOB=60°,AB=4CM,求矩形对角线的长是多少?
解:∵四边形ABCD是矩形
∴AC=BD AC=2AO BD=2BO
∴OA=OB
又∵∠AOB=60° AB=4cm
∴▲AOB是等边三角形
∴OA=AB=4cm
∴AC=BD=2 OA=8cm
A
B
C
D
O
应用新知 解决问题
(
变式:
如图,矩形ABCD的两条对角线相交于点O,已知∠BOC=120°,AB=6cm。求AC的长.
方法小结:如果矩形两对角线的夹角是60度或120度,
则其中必有等边三角形
A
B
C
D
O
矩形对角线
等边三角形
转化
60 °
能力提升
如图,将矩形ABCD沿着直线BD折叠,使点C落
在C’处,BC’交AD于点E,AD=8,AB=4,求三角形
BED的面积.
A
B
C
D
C’
1
2
3
E
解: ∵四边形ABCD是矩形
∴AD//BC,∠A=90° ∠2=∠3
又由折叠知∠1=∠2
∴∠1=∠3
∴BE=DE
设BE=DE=X,则AE=8-X
∵在Rt△ABE中,AB +AE =BE
∴4 +(8-X) =X
解得X=5,即DE=5
∴S△BED=1/2 DE ×AB=1/2×5×4=10
方法点拨 : 矩形的折叠问题常与勾股定理结合考察.
矩形的定义:
边
角
对角线
矩形对边平行且相等
矩形的四个角都是直角
矩形的对角线相等且互相平分
直角三角形斜边上的中线性质:
直角三角形斜边上的中线等于斜边的一半.
A
B
C
D
A
B
C
D
课堂小结
我的收获
1.知识:
有一个角是直角的平行四边形是矩形.
矩形的性质:
2.方法:类比探究
3.数学思想方法:
平行四边形 矩形
矩形
(特殊)
(一般)
直角三角形
等腰三角形
计算中找到等量关系,和勾股定理相结合,体现了数学学习中的转化和方程思想.
布置作业
必做:教材60页 3,4 题 61页8,9题.
选做:数学同步练习册47-48页.
