探索平行线的性质

课件26张PPT。探索平行线的性质Lm 知识回顾;
(1)什么是同位角、内错角、同旁内角?
(2)根据哪些条件可以判断两条直线互相平行?
猜猜看
如果已知两直线平行,那么同位角、内错角、同旁内角各有什么关系?
1、在练习本上画两条平行线AB、CD，再画直线MN与直线AB、CD相交（如下图）指出图中同位角、内错角、同旁内角2、将上图按照如下方式剪开，并分别把剪开得到的每对同位角、内错角重叠，你发现了什么？3、将图中的每对同旁内角剪成两部分，并把他们拼到一起去，你发现每对同旁内角之间有什么关系？? 做一做 ? 平行线的性质：两条平行线被第三条直线所截，内错角相等。简单地说，两直线平行，内错角相等。两条平行线被第三条直线所截，同旁内角互补。简单地说，两直线平行，同旁内角互补。两条平行线被第三条直线所截，同位角相等。简单地说，两直线平行，同位角相等。只有在两直线平行的条件下才有：同位角、内错角相等，同 旁内角互补。
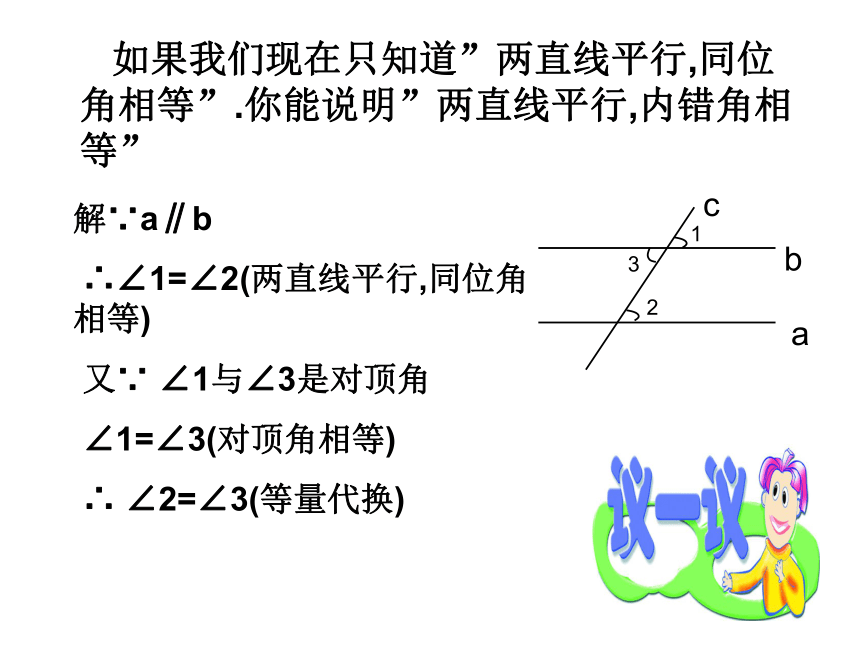
并不是所有的同位角、内错角都相等，同旁内角都互补 如果我们现在只知道”两直线平行,同位角相等”.你能说明”两直线平行,内错角相等” 你一定行:
请根据”两直线平行,同位角相等”,说明”两直线平行,同旁内角互补”成立的理由.例题1
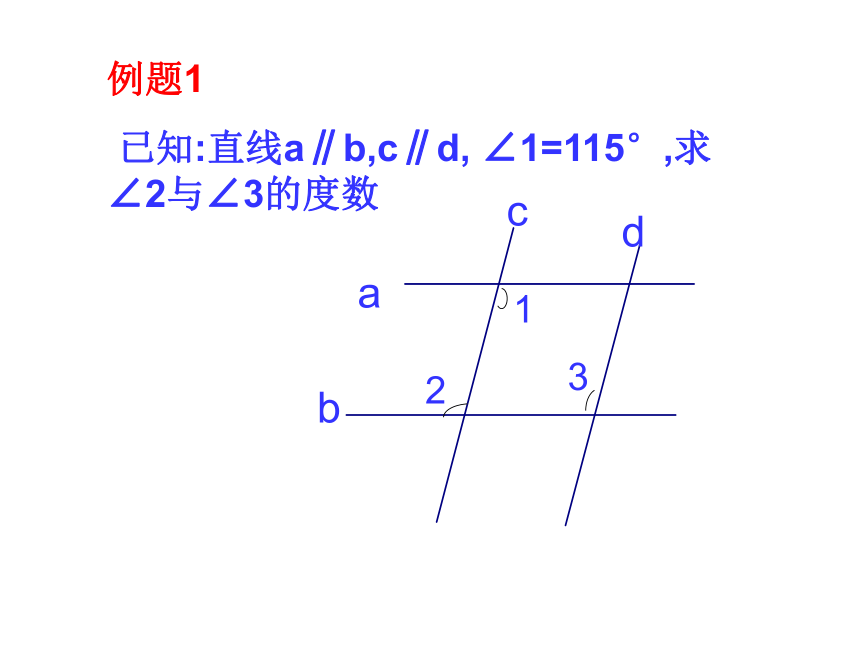
已知:直线a∥b,c∥d, ∠1=115°,求∠2与∠3的度数abcd231例题2:
如图:已知AB∥CD,求∠A+∠B+∠ACB的度数.
ABCD21例题3:
如图,AD∥BC, ∠A=∠C.试说明AB∥DC小结：
(1)平行线的三条性质
(2)利用平行线的三条性质解计算题和简单的解答
题ＤＣＤ3、已知，a∥b,c ∥d, ∠1=480
求： ∠2、 ∠3、 ∠4的度数 4 下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;③内-错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是- ( )
A.① B.②和③ C.④ D.①和④
5若两条平行线被第三条直线所截,则一组同位角的平分线互相 ( )
A.垂直 B.平行 C.重合 D.相交ab内错角相等，两直线平行∠4两直线平行，同位角相等∠5两直线平行，同旁内角互补ABCD同旁内角互补，两直线平行1800两直线平行，同旁内角互补解:∵AD∥BC
∴∠C=∠CDE(两直线平行,内错角相等)
又∵ ∠A=∠C
∴ ∠A=∠CDE(等量代换)
∴AB∥DC(同位角相等,两直线平行)例题4:做一做如图：AB,CD被EF所截，AB∥CD(填空)。
若∠1＝120o，则∠2＝ ＿＿ （ 　　　）
∠3＝ －∠1＝＿＿＿
（ 　　　　　）两直线平行，内错角相等。两直线平行，同旁内角互补。120o180o60o3、如图：已知∠1＝∠2，∠3＝65o ，求∠4的度数?例3 如图：已知AB∥CD,AD∥BC.判断∠1与∠2是否相等，并说明理由。例4 如图已知∠ABC＋∠c＝180o，
BD平分∠ABC. ∠CBD与∠D相等吗?
请说明理由。如图,已知:DE∥CB,∠1=∠2,求证:CD平分∠ECB. 再见 如图所示,已知AB∥CD,∠ABE=130°,∠CDE=152°,
求∠BED的度数.如图所示,AB∥CD,AD∥BC,∠A的2倍与∠C的3倍互补,求∠A和∠D的度数.如图9所示,AD∥BC,∠1=78°,∠2=40°,求∠ADC的度数.如图所示,AB∥CD,则∠A+∠E+∠F+∠C等于 ( )
A.180° B.360° C.540° D.720°如图所示,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,求∠DEG的度数.