三角形的内角和(1)[下学期]

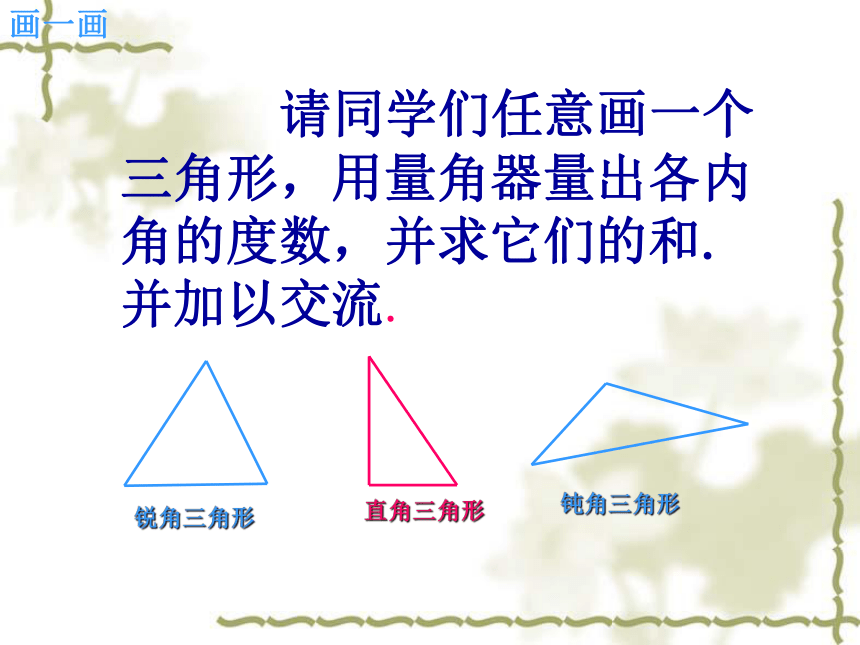
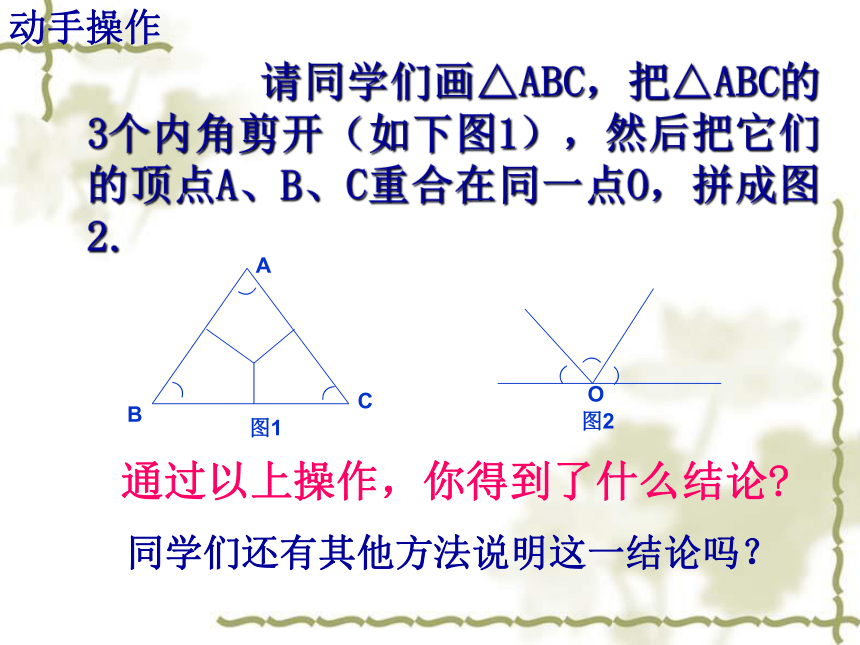
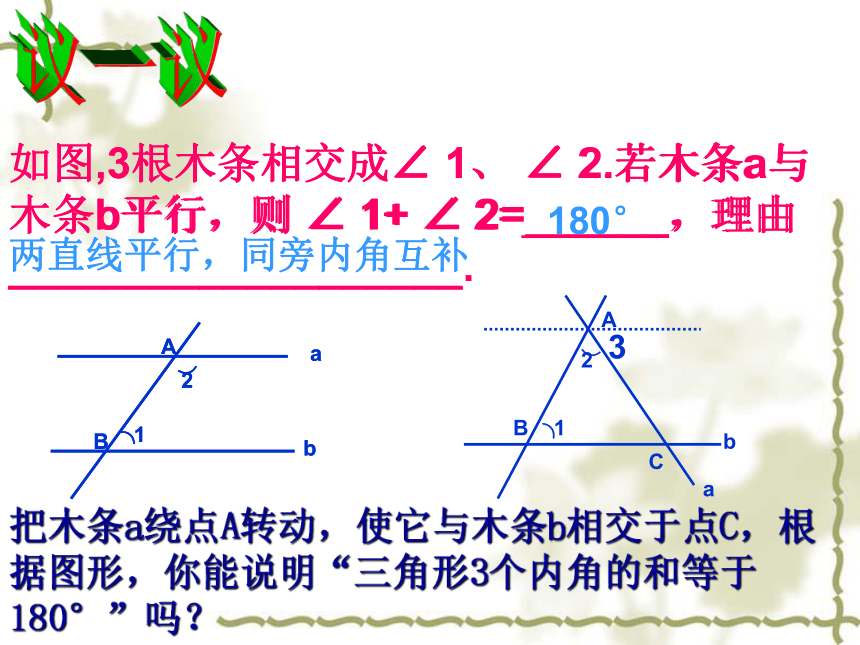
课件15张PPT。 三角形的内角和(1)画一画 请同学们任意画一个三角形，用量角器量出各内角的度数，并求它们的和.并加以交流.动手操作 请同学们画△ABC，把△ABC的3个内角剪开（如下图1），然后把它们的顶点A、B、C重合在同一点O，拼成图2.通过以上操作，你得到了什么结论? 同学们还有其他方法说明这一结论吗？议一议180°两直线平行，同旁内角互补把木条a绕点A转动，使它与木条b相交于点C，根据图形，你能说明“三角形3个内角的和等于180°”吗？3 解：∵ c//b,
∴ ∠3=∠4 （两直线平 行，内错角相等）
∠1+∠2+∠3=180°（两直 线平 行，同
旁内角互补）
∴ ∠1+∠2+∠4=180°
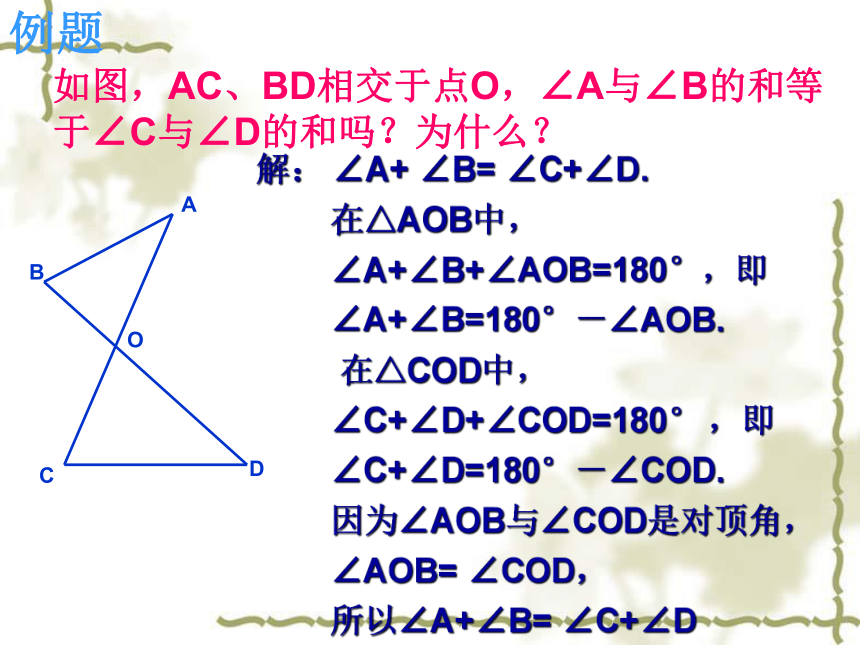
即△ABC的三个内角的和等于180°.例题如图，AC、BD相交于点O，∠A与∠B的和等于∠C与∠D的和吗？为什么？ 解： ∠A+ ∠B= ∠C+∠D.
在△AOB中，
∠A+∠B+∠AOB=180°，即
∠A+∠B=180°－∠AOB.
在△COD中，
∠C+∠D+∠COD=180° ，即
∠C+∠D=180°－∠COD.
因为∠AOB与∠COD是对顶角，
∠AOB= ∠COD，
所以∠A+∠B= ∠C+∠D
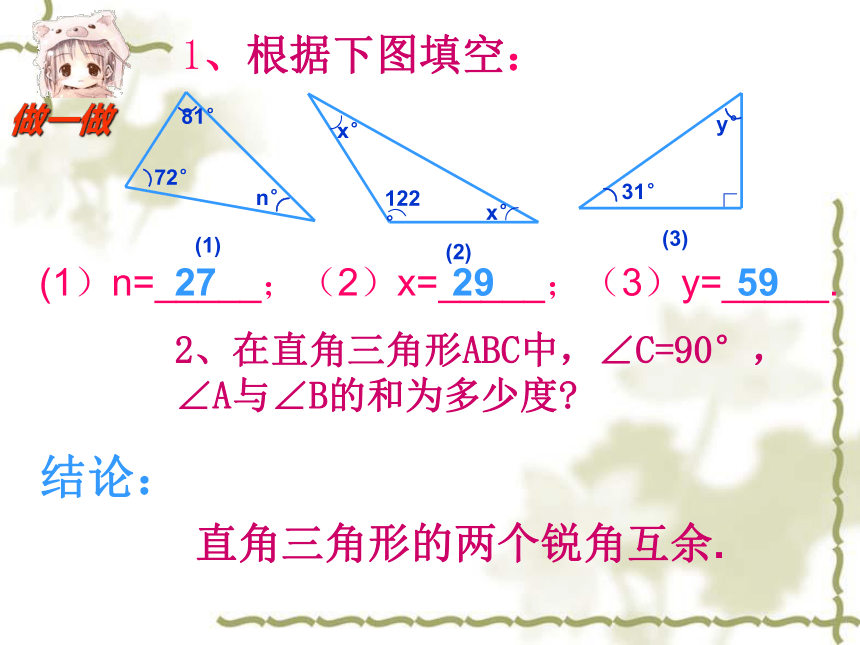
做一做2729592、在直角三角形ABC中，∠C=90°，∠A与∠B的和为多少度? 结论：直角三角形的两个锐角互余.试一试CBD度量∠A、∠C和∠CBD的度数.
你有什么发现？你能用所学的知
识加以说明吗? 因为∠A+∠C+∠CBA=________,
∠CBD+ ∠CBA=_________,
所以∠A+∠C_____ ∠CBD.180°180°=你知道吗？图中的∠CBD称为△ABC的一个外角.三角形的外角三角形的一边与另一边的延长线所组成的角，叫做三角形的外角 .练 一 练：1、求图中x和y的值.X=47X=50 Y=1402、(1)一个三角形的3个内角中，最多有几
个直角？最多有几个钝角？为什么？（2）直角三角形的外角可能是锐角吗？为什么？3、如图，AD是∠ABC的角平分线，E是BC延长线上一点，∠EAC=∠B. ∠ADE与∠DAE相等吗?为什么?解：∠ADE与∠DAE相等.
因为 ∠DAE= ∠DAC+ ∠EAC,
∠ADE是△ABD的一个外角,
∠ADE=∠B+ ∠BAD
因为 ∠BAD= ∠DAC, ∠EAC= ∠B,所以∠ADE= ∠DAE综 合 提 高如图，AB//CD，∠ABD与∠BDC的平分线相交于点E，求∠BED的度数.解：因为AB//CD，
所以∠ABD+∠BDC=180°，
因为BE平分∠ABD，DE平分∠BDC，
所以∠EBD= ∠ABD ，
∠BDE= ∠BDC，
所以∠EBD+ ∠BDE=90°，
在△BED中， ∠EBD+ ∠BDE+∠E=180°，
所以∠BED= 180°－ 90°=90°.
本节课你有什么收获？（1）重点探究了三角形3个内角之间的
关系以及三角形外角的性质.三角形3个内角的和等于180°.三角形的一个外角等于与它不相邻的两个内角的和.（2）由三角形3个内角之间的关系得到直
角三角形的一个性质：直角三角形的两个锐角互余. 布置作业:评价手册