《长方体和正方体整理和复习》(课件)五年级下册数学人教版(共19张PPT)
文档属性
| 名称 | 《长方体和正方体整理和复习》(课件)五年级下册数学人教版(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 05:29:28 | ||
图片预览






文档简介
(共19张PPT)
第10课时 整理和复习
长方体和正方体
义务教育人教版五年级下册
3
知识梳理
本单元学习了关于长方体和正方体的哪些知识?
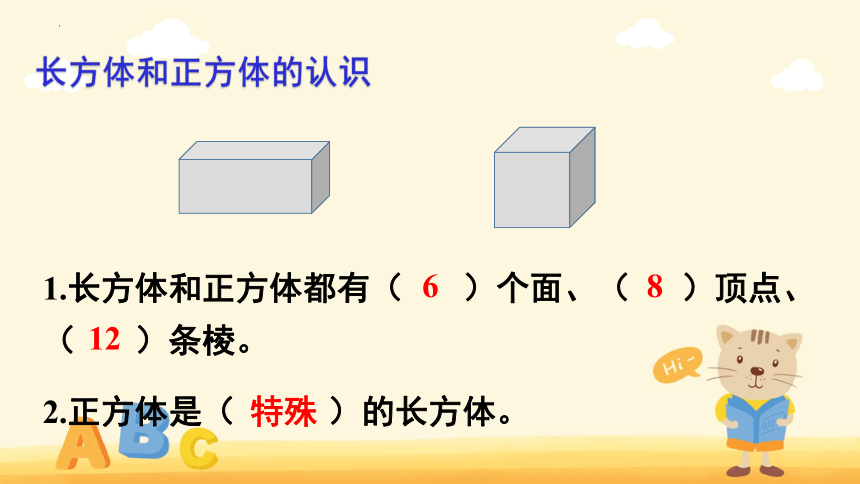
长方体和正方体的认识
1.长方体和正方体都有( )个面、( )顶点、( )条棱。
6
8
12
2.正方体是( )的长方体。
特殊
长方体和正方体的表面积
长方体的表面积=
正方体的表面积=
(长×宽+长×高+宽×高)×2
棱长×棱长×6
计算无盖物体及类似物体的表面积时,要注意面的个数。
长方体和正方体的体积
长方体的体积=
正方体的体积=
长×宽×高
棱长×棱长×棱长
长方体(或正方体)的体积=底面积×高
长方体和正方体的体积
体积(容积)单位间的进率:相邻两个体积单位之间的进率是( )。
1000
体积和容积单位间的关系:
1L=( )dm 1mL=( )cm
1
1
不规则物体的体积
你能用尺子和长方体(或正方体)容器测出右面物体的体积吗?如果用这种方法比较两个物体体积的大小,你打算怎么做?
玻璃球
绿豆
运用排水法求体积时,要把不规则物体完全浸没在水中。
一、基础练习
C
1.我会选。
(1)一瓶花露水的包装盒上印有“净含量100毫升”的字样,这个“100毫升”是指( )。
A.包装盒的体积 B.包装盒的容积 C.瓶中花露水的体积
(2)一个正方体的棱长扩大到原来的2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
A.2 B.4 C.8
B
C
1.我会选。
(3)一个长方体的棱长之和是180厘米,相交于一个顶点的三条棱的长度和是( )。
A.45厘米 B.30厘米 C.90厘米
(4)从一个长方体中挖掉一个角(如图),它的表面积( )。
A.比原来小 B.比原来大 C.与原来一样大
C
一、基础练习
A
一、基础练习
1.我会选。
(5)下列图形不能折成正方体的是( )。
A
B
C
C
二、易错练习
1.一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是9 dm、6 dm、3 dm,那么正方体的棱长是多少分米?它们的体积相等吗?
(9+6+3)×4=72(dm) 72÷12=6(dm )
长方体体积:9×6×3=162(dm3)
正方体体积:6×6×6=216(dm3)
答:不相等
输入标题
2.一个装有水的长方体容器,长是15cm,宽是8cm,现在水面离容器口2cm,如果将这个长方体橡皮泥浸没在里面,里面的水会溢出来吗?
9cm
4cm
6cm
2cm
8cm
15cm
9×6×4=216(cm3)
15×8×2=240(cm3)
216<240
答:容器里面的水不会溢出来。
二、易错练习
输入标题
3.一块长方形铁皮长30cm、宽15cm(如图所示),四个角上各剪掉边长5cm的正方形(每个正方形都相同),然后折起来做成没有盖子的长方体铁盒。这个铁盒的表面积是多少cm2?容积是多少cm3?
表面积:
30×15-5×5×4
=450-100
=350(cm2)
答:这个没盖铁盒的表面积是350cm2。
二、易错练习
3.一块长方形铁皮长30cm、宽15cm(如图所示),四个角上各剪掉边长5cm的正方形(每个正方形都相同),然后折起来做成没有盖子的长方体铁盒。这个铁盒的表面积是多少cm2?容积是多少cm3?
输入标题
容积:
长:30-5×2=20(cm)
宽:15-5×2=5(cm)
20×5×5=500(cm3)
答:这个没盖铁盒的容积是500cm3。
二、易错练习
4.一个长方体正好切成3个一样大的小正方体,3个小正方体表面积的总和比长方体的表面积大36平方厘米,原长方体的表面积是多少平方厘米?
36÷4×14
=9×14
=126(平方厘米)
答:原长方体的表面积是126平方厘米。
二、易错练习
三、拓展练习
1.一个长方体的底面是一个周长为20 cm的长方形,高为2 cm,如果长和宽的厘米数都是质数,那么这个长方体的体积是多少?
20÷2=10=3+7 3×7×2=42(cm3)
三、拓展练习
正方体的棱长是84÷3÷4=7(厘米)
原长方体的体积是7×7×(7-3)=196(立方厘米)
2.一个长方体,如果高增加3 cm,那么就变成一个正方体。这时表面积比原来增加84 cm2。原来长方体的体积是多少立方厘米?
课堂小结
通过这节课的学习,
你有什么收获
完成本课时的习题。
课后作业
第10课时 整理和复习
长方体和正方体
义务教育人教版五年级下册
3
知识梳理
本单元学习了关于长方体和正方体的哪些知识?
长方体和正方体的认识
1.长方体和正方体都有( )个面、( )顶点、( )条棱。
6
8
12
2.正方体是( )的长方体。
特殊
长方体和正方体的表面积
长方体的表面积=
正方体的表面积=
(长×宽+长×高+宽×高)×2
棱长×棱长×6
计算无盖物体及类似物体的表面积时,要注意面的个数。
长方体和正方体的体积
长方体的体积=
正方体的体积=
长×宽×高
棱长×棱长×棱长
长方体(或正方体)的体积=底面积×高
长方体和正方体的体积
体积(容积)单位间的进率:相邻两个体积单位之间的进率是( )。
1000
体积和容积单位间的关系:
1L=( )dm 1mL=( )cm
1
1
不规则物体的体积
你能用尺子和长方体(或正方体)容器测出右面物体的体积吗?如果用这种方法比较两个物体体积的大小,你打算怎么做?
玻璃球
绿豆
运用排水法求体积时,要把不规则物体完全浸没在水中。
一、基础练习
C
1.我会选。
(1)一瓶花露水的包装盒上印有“净含量100毫升”的字样,这个“100毫升”是指( )。
A.包装盒的体积 B.包装盒的容积 C.瓶中花露水的体积
(2)一个正方体的棱长扩大到原来的2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
A.2 B.4 C.8
B
C
1.我会选。
(3)一个长方体的棱长之和是180厘米,相交于一个顶点的三条棱的长度和是( )。
A.45厘米 B.30厘米 C.90厘米
(4)从一个长方体中挖掉一个角(如图),它的表面积( )。
A.比原来小 B.比原来大 C.与原来一样大
C
一、基础练习
A
一、基础练习
1.我会选。
(5)下列图形不能折成正方体的是( )。
A
B
C
C
二、易错练习
1.一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是9 dm、6 dm、3 dm,那么正方体的棱长是多少分米?它们的体积相等吗?
(9+6+3)×4=72(dm) 72÷12=6(dm )
长方体体积:9×6×3=162(dm3)
正方体体积:6×6×6=216(dm3)
答:不相等
输入标题
2.一个装有水的长方体容器,长是15cm,宽是8cm,现在水面离容器口2cm,如果将这个长方体橡皮泥浸没在里面,里面的水会溢出来吗?
9cm
4cm
6cm
2cm
8cm
15cm
9×6×4=216(cm3)
15×8×2=240(cm3)
216<240
答:容器里面的水不会溢出来。
二、易错练习
输入标题
3.一块长方形铁皮长30cm、宽15cm(如图所示),四个角上各剪掉边长5cm的正方形(每个正方形都相同),然后折起来做成没有盖子的长方体铁盒。这个铁盒的表面积是多少cm2?容积是多少cm3?
表面积:
30×15-5×5×4
=450-100
=350(cm2)
答:这个没盖铁盒的表面积是350cm2。
二、易错练习
3.一块长方形铁皮长30cm、宽15cm(如图所示),四个角上各剪掉边长5cm的正方形(每个正方形都相同),然后折起来做成没有盖子的长方体铁盒。这个铁盒的表面积是多少cm2?容积是多少cm3?
输入标题
容积:
长:30-5×2=20(cm)
宽:15-5×2=5(cm)
20×5×5=500(cm3)
答:这个没盖铁盒的容积是500cm3。
二、易错练习
4.一个长方体正好切成3个一样大的小正方体,3个小正方体表面积的总和比长方体的表面积大36平方厘米,原长方体的表面积是多少平方厘米?
36÷4×14
=9×14
=126(平方厘米)
答:原长方体的表面积是126平方厘米。
二、易错练习
三、拓展练习
1.一个长方体的底面是一个周长为20 cm的长方形,高为2 cm,如果长和宽的厘米数都是质数,那么这个长方体的体积是多少?
20÷2=10=3+7 3×7×2=42(cm3)
三、拓展练习
正方体的棱长是84÷3÷4=7(厘米)
原长方体的体积是7×7×(7-3)=196(立方厘米)
2.一个长方体,如果高增加3 cm,那么就变成一个正方体。这时表面积比原来增加84 cm2。原来长方体的体积是多少立方厘米?
课堂小结
通过这节课的学习,
你有什么收获
完成本课时的习题。
课后作业
