第九章 统计 培优训练-2022-2023学年高一下学期数学人教A版(2019)必修第二册(含答案)
文档属性
| 名称 | 第九章 统计 培优训练-2022-2023学年高一下学期数学人教A版(2019)必修第二册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 359.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 00:00:00 | ||
图片预览




文档简介
《第九章 统计》培优训练
一、单项选择题
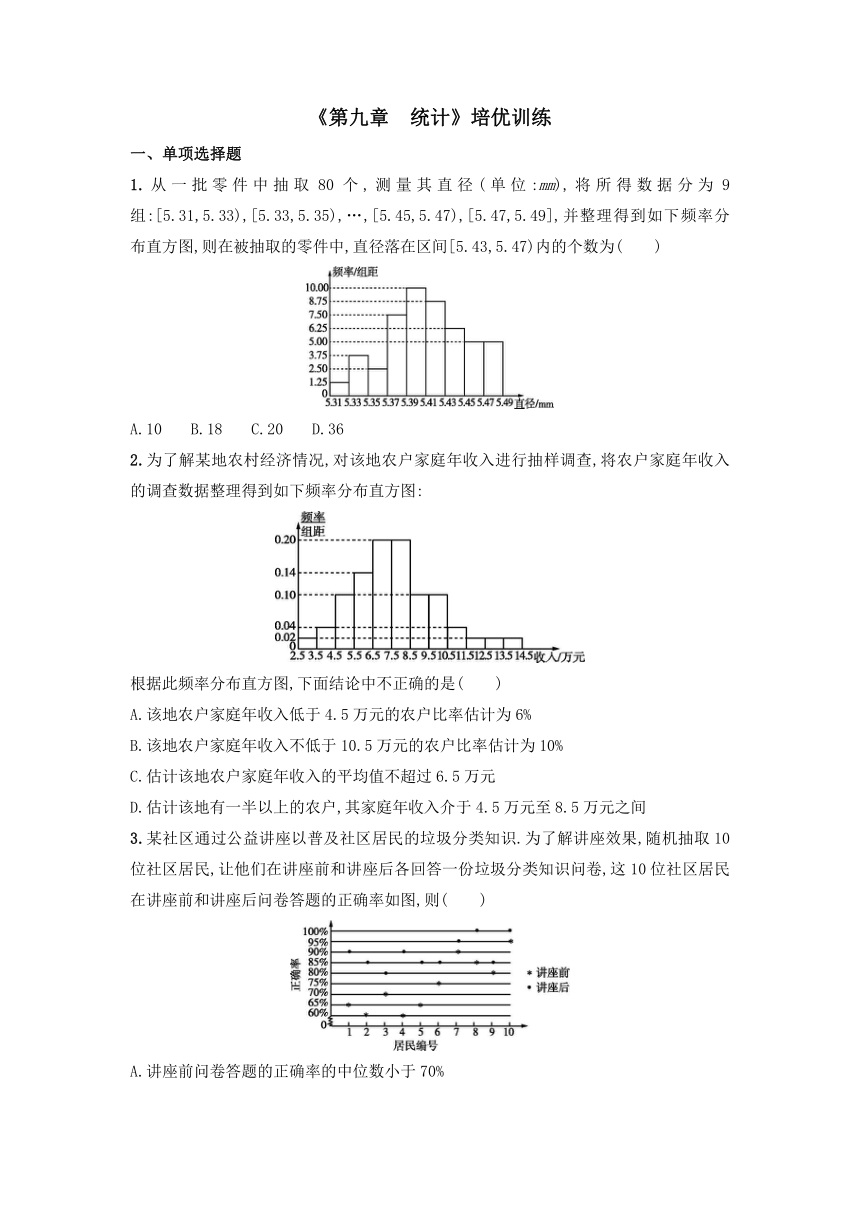
1.从一批零件中抽取80个,测量其直径(单位:mm),将所得数据分为9组:[5.31,5.33),[5.33,5.35),…,[5.45,5.47),[5.47,5.49],并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间[5.43,5.47)内的个数为( )
A.10 B.18 C.20 D.36
2.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
3.某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如图,则( )
A.讲座前问卷答题的正确率的中位数小于70%
B.讲座后问卷答题的正确率的平均数大于85%
C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差
4.在一组样本数据中,1,2,3,4出现的频率分别为p1,p2,p3,p4,且pi=1,则下面四种情形中,对应样本的标准差最大的一组是( )
A.p1=p4=0.1,p2=p3=0.4
B.p1=p4=0.4,p2=p3=0.1
C.p1=p4=0.2,p2=p3=0.3
D.p1=p4=0.3,p2=p3=0.2
5.设一组样本数据x1,x2,…,xn的方差为0.01,则数据10x1,10x2,…,10xn的方差为( )
A.0.01 B.0.1 C.1 D.10
6.“一世”又叫“一代”.东汉·王充《论衡·宜汉篇》:“且孔子所谓一世,三十年也”,清代·段玉裁《说文解字注》:“三十年为一世,按父子相继曰世”.而当代中国学者测算“一代”平均为25年.另根据国际一家研究机构的研究报告显示,全球家族企业的平均寿命其实只有26年,约占总量的28%的家族企业只能传到第二代,约占总量的14%的家族企业只能传到第三代,约占总量4%的家族企业可以传到第四代甚至更久远(为了研究方便,超过四代的可忽略不计).根据该研究机构的研究报告,可以估计该机构所认为的“一代”大约为( )
A.23年 B.22年 C.21年 D.20年
二、多项选择题
7.有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样本数据的样本极差相同
8.如图所示的两个扇形图分别表示了某地2010年和2020年小学生参加课外兴趣班的情况,已知2020年当地小学生参加课外兴趣班的总人数是2010年当地小学生参加课外兴趣班的总人数的4倍,则下列说法正确的是( )
A.2020年参加音乐兴趣班的小学生人数是2010年参加音乐兴趣班的小学生人数的4倍
B.这10年间,参加编程兴趣班的小学生人数变化最大
C.2020年参加美术兴趣班的小学生人数少于2010年参加美术兴趣班的小学生人数
D.相对于2010年,2020年参加不同课外兴趣班的小学生人数更平均
9.下列统计量中可用于度量样本x1,x2,…,xn离散程度的有( )
A.x1,x2,…,xn的标准差
B.x1,x2,…,xn的中位数
C.x1,x2,…,xn的极差
D.x1,x2,…,xn的平均数
10.某企业为响应国家新旧动能转换的号召,积极调整企业拥有的5种系列产品的结构比例,并坚持自主创新提升产业技术水平,2021年年总收入是2020年的2倍,为了更好地总结5种系列产品的年收入变化情况,统计了这两年5种系列产品的年收入构成比例,得到如下扇形图:
则下列结论正确的是( )
A.2021年的甲系列产品收入和2020年相同
B.2021年的丁系列产品收入是2020年丁系列产品收入的4倍
C.2021年的丙和丁系列产品的收入之和比2020年的企业年总收入还多
D.2021年的乙和丙系列产品的收入之和比2020年的乙和丙系列产品收入之和的2倍要少
三、解答题
11.某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:m2)和材积量(单位:m3),得到如下数据:
样本号i 1 2 3 4 5 6 7 8 9 10 总和
根部横截面积xi 0.04 0.06 0.04 0.08 0.08 0.05 0.05 0.07 0.07 0.06 0.6
材积量yi 0.25 0.40 0.22 0.54 0.51 0.34 0.36 0.46 0.42 0.40 3.9
并计算得=0.038,=1.615 8,xiyi=0.247 4.
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量.
(2)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为186 m2.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
12.某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 9.8 10.3 10.0 10.2 9.9
新设备 10.1 10.4 10.1 10.0 10.1
旧设备 9.8 10.0 10.1 10.2 9.7
新设备 10.3 10.6 10.5 10.4 10.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和.
(1)求,,,;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果≥2,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
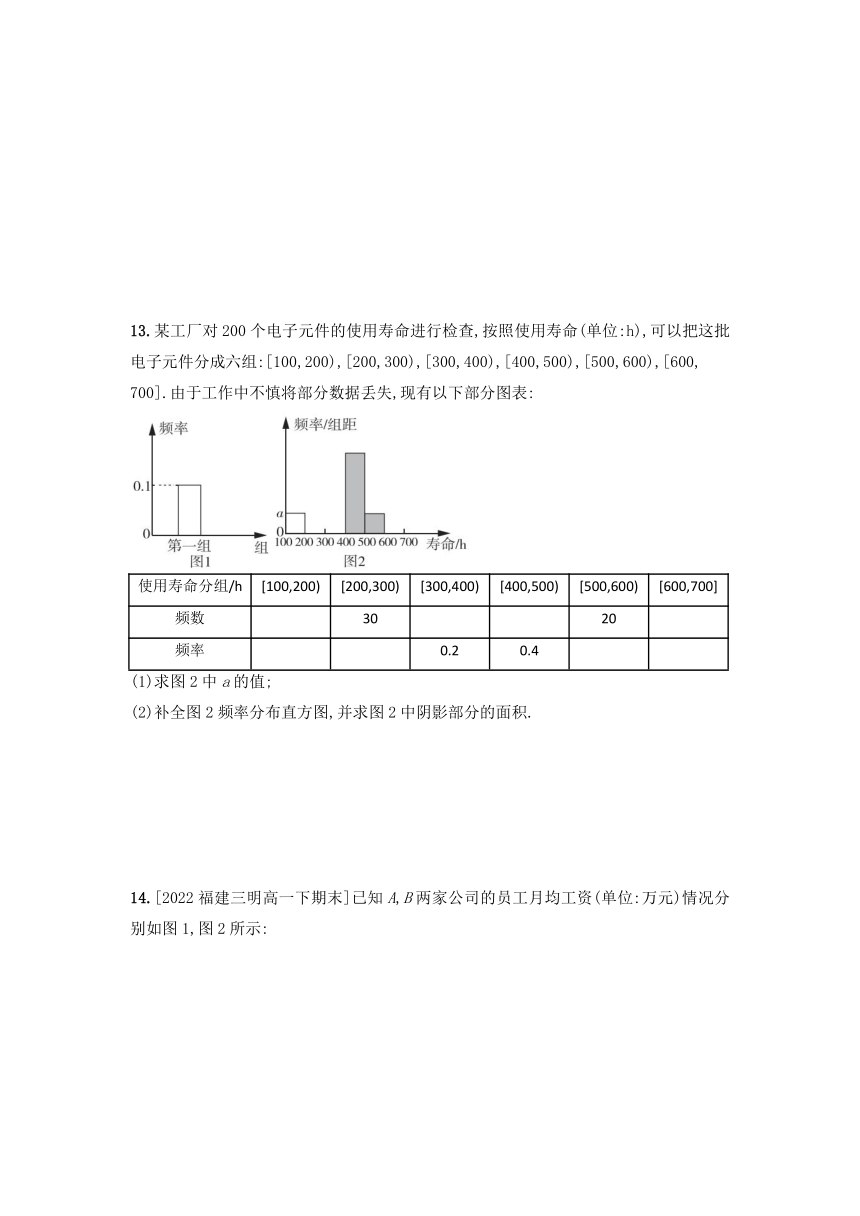
13.某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h),可以把这批电子元件分成六组:[100,200),[200,300),[300,400),[400,500),[500,600),[600,
700].由于工作中不慎将部分数据丢失,现有以下部分图表:
使用寿命分组/h [100,200) [200,300) [300,400) [400,500) [500,600) [600,700]
频数 30 20
频率 0.2 0.4
(1)求图2中a的值;
(2)补全图2频率分布直方图,并求图2中阴影部分的面积.
14.[2022福建三明高一下期末]已知A,B两家公司的员工月均工资(单位:万元)情况分别如图1,图2所示:
(1)以每组数据的区间中点值为代表,根据图1估计A公司员工月均工资的平均数、中位数,你认为用哪个数据更能反映该公司普通员工的工资水平 请说明理由.
(2)小明拟到A,B两家公司中的一家应聘,以公司普通员工的工资水平作为决策依据,他应该选哪个公司
15. 某公司为了解用户对其产品的满意程度,采用分层随机抽样的方法从A,B两个地区共抽取了500名用户,用户根据满意程度对该公司产品进行评分(满分:100分),该公司将收集到的数据按照[20,40),[40,60),[60,80),[80,100]进行分组,绘制成如图所示的频率分布直方图.已知A地区用户约为40 000人,B地区用户约为10 000人.
(1)求该公司采用分层随机抽样的方法从A,B两个地区分别抽取的用户人数;
(2)估计B地区所有用户中,对该产品评分不低于80分的用户的人数;
(3)估计A地区用户对该公司产品的评分的平均值为μ1,B地区用户对该公司产品的评分的平均值为μ2,以及A,B两个地区所有用户对该公司产品的评分的平均值为μ0,试比较μ0和的大小,并说明理由.
16.为进一步推动防范电信网络诈骗工作,预防和减少电信网络诈骗案件的发生,某市开展防骗知识大宣传活动.该市年龄在100岁及以下的居民人口约为300万人,从0岁到100岁的居民年龄频率分布直方图如图所示.为了解防骗知识宣传的效果,随机调查了100名该市年龄100岁及以下居民对防骗知识的知晓情况,调查的知晓率(被调查的人群中,知晓的人数和总人数的比率)如表所示.
年龄段 [0,20) [20,40) [40,60) [60,80) [80,100]
知晓率/% 34 45 54 65 74
(1)根据频率分布直方图,估计该市年龄100岁及以下居民的平均年龄(同一组中的数据用该组区间的中点值作代表);
(2)利用样本估计总体的思想,估计该市年龄100岁及以下居民对防骗知识的知晓率;
(3)根据《中国电信网络诈骗分析报告》显示,老年人(年龄60岁及以上)为易受骗人群,但调查中发现年龄在[60,100]的人群比[0,60)的人群对防骗知识的知晓率高.请从统计学的角度分析调查结果与实际情况产生差异的原因(至少写出两点).
参考答案
一、单项选择题
1.B 由题知[5.43,5.45),[5.45,5.47)所对应的小矩形的高分别为6.25,5.00,所以[5.43,5.47)的频率为(6.25+5.00)×0.02=0.225,所以直径落在区间[5.43,5.47)内的个数为80×0.225=18,故选B.
2.C 对于A,根据频率分布直方图,可知该地农户家庭年收入低于4.5万元的农户比率约为(0.02+0.04)×1×100%=6%,故A结论正确;对于B,根据频率分布直方图,可知该地农户家庭年收入不低于10.5万元的农户比率约为(0.04+0.02+0.02+0.02)×1×100%=10%,故B结论正确;对于C,根据频率分布直方图,可知该地农户家庭年收入的平均值约为3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68(万元),故C结论错误;对于D,根据频率分布直方图,可知家庭年收入介于4.5万元至8.5万元之间的农户比率约为(0.10+0.14+0.20+0.20)×1×100%=64%>50%,故D结论正确.
3.B 对于A,讲座前问卷答题的正确率的中位数是=72.5%,所以A错误;对于B,讲座后问卷答题的正确率分别是80%,85%,85%,85%,85%,90%,90%,95%,100%,100%,其平均数显然大于85%,所以B正确;对于C,由题图可知,讲座前问卷答题的正确率波动较大,讲座后问卷答题的正确率波动较小,所以讲座前问卷答题的正确率的标准差大于讲座后问卷答题的正确率的标准差,所以C错误;对于D,讲座前问卷答题的正确率的极差是95%-60%=35%,讲座后问卷答题的正确率的极差是100%-80%=20%,所以讲座前问卷答题的正确率的极差大于讲座后问卷答题的正确率的极差,所以D错误.故选B.
4.B 对于A,样本的平均数=1×0.1+2×0.4+3×0.4+4×0.1=2.5,方差=(1-2.5)2×0.1+(2-2.5)2×0.4+(3-2.5)2×0.4+(4-2.5)2×0.1=1.52×0.1+0.52×0.4+0.52×0.4+1.52×0.1=0.65,所以s1=.对于B,样本的平均数=1×0.4+2×0.1+3×0.1+
4×0.4=2.5,方差=(1-2.5)2×0.4+(2-2.5)2×0.1+(3-2.5)2×0.1+(4-2.5)2×0.4=1.52×0.4+0.52×0.1+0.52×0.1+1.52×0.4=1.85,所以s2=.对于C,样本的平均数=1×0.2+2×0.3+3×0.3+4×0.2=2.5,方差=(1-2.5)2×0.2+(2-2.5)2×0.3+(3-2.5)2×0.3+(4-2.5)2×0.2=1.52×0.2+0.52×0.3+0.52×0.3+1.52×0.2=1.05,所以s3=.对于D,样本的平均数=1×0.3+2×0.2+3×0.2+4×0.3=2.5,方差=(1-2.5)2×0.3+(2-2.5)2×0.2+(3-2.5)2×0.2+(4-2.5)2×0.3=1.52×0.3+0.52×0.2+0.52×0.2+1.52×0.3=1.45,所以s4=.所以B中的标准差最大.
5.C 因为样本数据x1,x2,…,xn的方差为0.01,D(aX)=a2D(X),所以样本数据10x1,10x2,…,10xn的方差为102×0.01=1,故选C.
6.B 设“一代”为x年,由题意得企业寿命的频率分布表为:
家族企业寿命 频率
[0,x) 54%
[x,2x) 28%
[2x,3x) 14%
[3x,4x] 4%
所以家族企业的平均寿命为0.54×0.5x+0.28×1.5x+0.14×2.5x+0.04×3.5x=26,解得x≈22.
二、多项选择题
7.CD 设样本数据x1,x2,…,xn的平均数、中位数、标准差、极差分别为,m,s,t,依题意,得新样本数据y1,y2,…,yn的平均数、中位数、标准差、极差分别为+c,m+c,s,t,因为c≠0,所以C,D正确,故选CD.
8.ABD 设2010年参加课外兴趣班的小学生总人数为a,则2020年参加课外兴趣班的小学生总人数是4a.由题中扇形图,知2010年和2020年参加音乐兴趣班的小学生人数分别为a×21%=0.21a,4a×21%=0.84a,故A正确;这10年间参加编程兴趣班的小学生人数变化量为4a×32%-a×5%=1.23a,参加语言表演兴趣班的小学生人数变化量为4a×20%-a×14%=0.66a,参加音乐兴趣班的小学生人数变化量为4a×21%-a×21%=0.63a,参加美术兴趣班的小学生人数变化量为4a×27%-a×60%=0.48a,因为1.23a>0.66a>0.63a>0.48a,所以这10年间参加编程兴趣班的小学生人数变化量最大,故B正确,C错误;根据题中扇形图中的比例分布,可知D正确.故选ABD.
9.AC 平均数、众数和中位数均刻画了样本数据的集中趋势,一般地,对数值型数据集中趋势的描述,可以用平均数和中位数,对分类型数据集中趋势的描述,可以用众数.方差、标准差和极差均是度量样本数据离散程度的.故选AC.
10.ABC 设2020年年总收入为W,则2021年年总收入为2W,观察扇形图可知:
A √ 2020年的甲系列产品收入为0.4W,2021年的甲系列产品收入为2W×20%=0.4W.
B √ 2020年的丁系列产品收入为0.15W,2021年的丁系列产品收入为2W×30%=0.6W,0.6W=4×0.15W.
C √ 2021年的丙和丁系列产品的收入之和为2W×(30%+25%)=1.1W>W.
D 2020年的乙和丙系列产品收入之和为(10%+20%)W=0.3W,2021年的乙和丙系列产品的收入之和为2W×(20%+25%)=0.9W,显然0.9W>2×0.3W.
三、解答题
11.解析(1)估计该林区这种树木平均一棵的根部横截面积=0.06,
估计该林区这种树木平均一棵的材积量=0.39.
(2)设该林区这种树木的总材积量的估计值为Y m3,由题意可知,该种树木的材积量与其根部横截面积近似成正比,所以,
所以Y==1 209,即该林区这种树木的总材积量的估计值为1 209 m3.
12.解析(1)由表格中的数据易得
×(-0.2+0.3+0+0.2-0.1-0.2+0+0.1+0.2-0.3)+10.0=10.0,
×(0.1+0.4+0.1+0+0.1+0.3+0.6+0.5+0.4+0.5)+10.0=10.3,
×[(9.7-10.0)2+2×(9.8-10.0)2+(9.9-10.0)2+2×(10.0-10.0)2+(10.1-10.0)2+2×(10.2-10.0)2+(10.3-10.0)2]=0.036,
×[(10.0-10.3)2+3×(10.1-10.3)2+(10.3-10.3)2+2×(10.4-10.3)2+2×(10.5-10.3)2+(10.6-10.3)2]=0.04.
(2)由(1)中数据可得=10.3-10.0=0.3,
2,
显然有>2成立,
所以认为新设备生产产品的该项指标的均值较旧设备有显著提高.
13.解析(1)由题意可知0.1=a×100,所以a=0.001.
(2)补全后的频率分布直方图如图所示,
阴影部分的面积为0.004×100+0.001×100=0.5.
14.解析(1)A公司员工月均工资的平均数为0.3×0.21+0.5×0.29+0.7×0.27+0.9×0.21+29×0.02=1.166(万元).
由题图1可知A公司员工月均工资在0.6万元以下的比例为0.21+0.29=0.5,
所以A公司员工月均工资的中位数约为0.6万元.
用中位数更能反映该公司普通员工的工资水平,理由如下:
因为平均数受每一个数据的影响,越离群的数据对平均数的影响越大,该公司少数员工的月收入很高,在这种情况下平均数并不能较好地反映普通员工的收入水平,而中位数不受少数极端数据的影响,可以较好地反映普通员工的收入水平.
(2)B公司员工月均工资的平均数为(0.3×0.375+0.5×0.750+0.7×2.750+0.9×1.000+1.1×0.125)×0.2=0.69(万元).
由题图2知,B公司员工月均工资在0.6万元以下的频率为(0.375+0.75)×0.2=0.225,
在0.8万元以下的频率为(0.375+0.750+2.750)×0.2=0.775.
设B公司员工月均工资的中位数为x万元,则(x-0.6)×2.750=0.5-0.225,得x=0.7.
小明应选择B公司应聘,理由如下:
B公司员工工资数据较为集中,月均工资的平均数和中位数均能反映该公司普通员工的平均收入水平,B公司员工月均工资平均数为0.69,中位数为0.7,均大于A公司员工月均工资的中位数0.62,所以以公司普通员工的工资水平作为决策依据,小明应该选B公司应聘.
15.解析(1)设从A,B两个地区抽取的用户人数分别为x,y,则,所以x=400,y=500-400=100.
所以该公司采用分层随机抽样的方法,从A,B两个地区抽取的用户人数分别为400和100.
(2)由频率分布直方图,知B地区抽取的用户中,对该产品评分不低于80分的用户频率为0.005×20=0.1,
所以估计B地区所有用户中,对该产品评分不低于80分的用户人数为0.1×10 000=1 000.
(3)μ0>.理由如下:
由(1)知μ0=,
所以μ0-.
又μ1=30×0.005×20+50×0.015×20+70×0.020×20+90×0.010×20=64,
μ2=30×0.015×20+50×0.010×20+70×0.020×20+90×0.005×20=56,
所以μ1>μ2,所以>0,所以μ0>.
16.解析(1)根据频率分布直方图,得(0.01+0.013+a+0.007+0.002)×20=1,
解得a=0.018.
由频率分布直方图可估计平均数为
10×0.01×20+30×0.013×20+50×0.018×20+70×0.007×20+90×0.002×20=41.2,
所以估计该市年龄100岁及以下居民的平均年龄为41.2岁.
(2)被调查的100名居民中,年龄处在[0,20),[20,40),[40,60),[60,80),[80,100]的人数分别为20,26,36,14,4.
由表格,得这100名居民对防骗知识的知晓率为×(20×0.34+26×0.45+36×0.54+14×0.65+4×0.74)=50%,
所以估计该市年龄100岁及以下居民对防骗知识的知晓率为50%.
(3)原因分析:
①样本数据过少,不能很好地反映总体数据的特征;
②调查的人数中年龄在[60,100]的只有18人,也许这部分人刚好对防骗知识的知晓率高,从而导致调查结果不能很好地代表实际情况.
一、单项选择题
1.从一批零件中抽取80个,测量其直径(单位:mm),将所得数据分为9组:[5.31,5.33),[5.33,5.35),…,[5.45,5.47),[5.47,5.49],并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间[5.43,5.47)内的个数为( )
A.10 B.18 C.20 D.36
2.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
3.某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如图,则( )
A.讲座前问卷答题的正确率的中位数小于70%
B.讲座后问卷答题的正确率的平均数大于85%
C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差
4.在一组样本数据中,1,2,3,4出现的频率分别为p1,p2,p3,p4,且pi=1,则下面四种情形中,对应样本的标准差最大的一组是( )
A.p1=p4=0.1,p2=p3=0.4
B.p1=p4=0.4,p2=p3=0.1
C.p1=p4=0.2,p2=p3=0.3
D.p1=p4=0.3,p2=p3=0.2
5.设一组样本数据x1,x2,…,xn的方差为0.01,则数据10x1,10x2,…,10xn的方差为( )
A.0.01 B.0.1 C.1 D.10
6.“一世”又叫“一代”.东汉·王充《论衡·宜汉篇》:“且孔子所谓一世,三十年也”,清代·段玉裁《说文解字注》:“三十年为一世,按父子相继曰世”.而当代中国学者测算“一代”平均为25年.另根据国际一家研究机构的研究报告显示,全球家族企业的平均寿命其实只有26年,约占总量的28%的家族企业只能传到第二代,约占总量的14%的家族企业只能传到第三代,约占总量4%的家族企业可以传到第四代甚至更久远(为了研究方便,超过四代的可忽略不计).根据该研究机构的研究报告,可以估计该机构所认为的“一代”大约为( )
A.23年 B.22年 C.21年 D.20年
二、多项选择题
7.有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样本数据的样本极差相同
8.如图所示的两个扇形图分别表示了某地2010年和2020年小学生参加课外兴趣班的情况,已知2020年当地小学生参加课外兴趣班的总人数是2010年当地小学生参加课外兴趣班的总人数的4倍,则下列说法正确的是( )
A.2020年参加音乐兴趣班的小学生人数是2010年参加音乐兴趣班的小学生人数的4倍
B.这10年间,参加编程兴趣班的小学生人数变化最大
C.2020年参加美术兴趣班的小学生人数少于2010年参加美术兴趣班的小学生人数
D.相对于2010年,2020年参加不同课外兴趣班的小学生人数更平均
9.下列统计量中可用于度量样本x1,x2,…,xn离散程度的有( )
A.x1,x2,…,xn的标准差
B.x1,x2,…,xn的中位数
C.x1,x2,…,xn的极差
D.x1,x2,…,xn的平均数
10.某企业为响应国家新旧动能转换的号召,积极调整企业拥有的5种系列产品的结构比例,并坚持自主创新提升产业技术水平,2021年年总收入是2020年的2倍,为了更好地总结5种系列产品的年收入变化情况,统计了这两年5种系列产品的年收入构成比例,得到如下扇形图:
则下列结论正确的是( )
A.2021年的甲系列产品收入和2020年相同
B.2021年的丁系列产品收入是2020年丁系列产品收入的4倍
C.2021年的丙和丁系列产品的收入之和比2020年的企业年总收入还多
D.2021年的乙和丙系列产品的收入之和比2020年的乙和丙系列产品收入之和的2倍要少
三、解答题
11.某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:m2)和材积量(单位:m3),得到如下数据:
样本号i 1 2 3 4 5 6 7 8 9 10 总和
根部横截面积xi 0.04 0.06 0.04 0.08 0.08 0.05 0.05 0.07 0.07 0.06 0.6
材积量yi 0.25 0.40 0.22 0.54 0.51 0.34 0.36 0.46 0.42 0.40 3.9
并计算得=0.038,=1.615 8,xiyi=0.247 4.
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量.
(2)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为186 m2.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
12.某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 9.8 10.3 10.0 10.2 9.9
新设备 10.1 10.4 10.1 10.0 10.1
旧设备 9.8 10.0 10.1 10.2 9.7
新设备 10.3 10.6 10.5 10.4 10.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和.
(1)求,,,;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果≥2,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
13.某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h),可以把这批电子元件分成六组:[100,200),[200,300),[300,400),[400,500),[500,600),[600,
700].由于工作中不慎将部分数据丢失,现有以下部分图表:
使用寿命分组/h [100,200) [200,300) [300,400) [400,500) [500,600) [600,700]
频数 30 20
频率 0.2 0.4
(1)求图2中a的值;
(2)补全图2频率分布直方图,并求图2中阴影部分的面积.
14.[2022福建三明高一下期末]已知A,B两家公司的员工月均工资(单位:万元)情况分别如图1,图2所示:
(1)以每组数据的区间中点值为代表,根据图1估计A公司员工月均工资的平均数、中位数,你认为用哪个数据更能反映该公司普通员工的工资水平 请说明理由.
(2)小明拟到A,B两家公司中的一家应聘,以公司普通员工的工资水平作为决策依据,他应该选哪个公司
15. 某公司为了解用户对其产品的满意程度,采用分层随机抽样的方法从A,B两个地区共抽取了500名用户,用户根据满意程度对该公司产品进行评分(满分:100分),该公司将收集到的数据按照[20,40),[40,60),[60,80),[80,100]进行分组,绘制成如图所示的频率分布直方图.已知A地区用户约为40 000人,B地区用户约为10 000人.
(1)求该公司采用分层随机抽样的方法从A,B两个地区分别抽取的用户人数;
(2)估计B地区所有用户中,对该产品评分不低于80分的用户的人数;
(3)估计A地区用户对该公司产品的评分的平均值为μ1,B地区用户对该公司产品的评分的平均值为μ2,以及A,B两个地区所有用户对该公司产品的评分的平均值为μ0,试比较μ0和的大小,并说明理由.
16.为进一步推动防范电信网络诈骗工作,预防和减少电信网络诈骗案件的发生,某市开展防骗知识大宣传活动.该市年龄在100岁及以下的居民人口约为300万人,从0岁到100岁的居民年龄频率分布直方图如图所示.为了解防骗知识宣传的效果,随机调查了100名该市年龄100岁及以下居民对防骗知识的知晓情况,调查的知晓率(被调查的人群中,知晓的人数和总人数的比率)如表所示.
年龄段 [0,20) [20,40) [40,60) [60,80) [80,100]
知晓率/% 34 45 54 65 74
(1)根据频率分布直方图,估计该市年龄100岁及以下居民的平均年龄(同一组中的数据用该组区间的中点值作代表);
(2)利用样本估计总体的思想,估计该市年龄100岁及以下居民对防骗知识的知晓率;
(3)根据《中国电信网络诈骗分析报告》显示,老年人(年龄60岁及以上)为易受骗人群,但调查中发现年龄在[60,100]的人群比[0,60)的人群对防骗知识的知晓率高.请从统计学的角度分析调查结果与实际情况产生差异的原因(至少写出两点).
参考答案
一、单项选择题
1.B 由题知[5.43,5.45),[5.45,5.47)所对应的小矩形的高分别为6.25,5.00,所以[5.43,5.47)的频率为(6.25+5.00)×0.02=0.225,所以直径落在区间[5.43,5.47)内的个数为80×0.225=18,故选B.
2.C 对于A,根据频率分布直方图,可知该地农户家庭年收入低于4.5万元的农户比率约为(0.02+0.04)×1×100%=6%,故A结论正确;对于B,根据频率分布直方图,可知该地农户家庭年收入不低于10.5万元的农户比率约为(0.04+0.02+0.02+0.02)×1×100%=10%,故B结论正确;对于C,根据频率分布直方图,可知该地农户家庭年收入的平均值约为3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68(万元),故C结论错误;对于D,根据频率分布直方图,可知家庭年收入介于4.5万元至8.5万元之间的农户比率约为(0.10+0.14+0.20+0.20)×1×100%=64%>50%,故D结论正确.
3.B 对于A,讲座前问卷答题的正确率的中位数是=72.5%,所以A错误;对于B,讲座后问卷答题的正确率分别是80%,85%,85%,85%,85%,90%,90%,95%,100%,100%,其平均数显然大于85%,所以B正确;对于C,由题图可知,讲座前问卷答题的正确率波动较大,讲座后问卷答题的正确率波动较小,所以讲座前问卷答题的正确率的标准差大于讲座后问卷答题的正确率的标准差,所以C错误;对于D,讲座前问卷答题的正确率的极差是95%-60%=35%,讲座后问卷答题的正确率的极差是100%-80%=20%,所以讲座前问卷答题的正确率的极差大于讲座后问卷答题的正确率的极差,所以D错误.故选B.
4.B 对于A,样本的平均数=1×0.1+2×0.4+3×0.4+4×0.1=2.5,方差=(1-2.5)2×0.1+(2-2.5)2×0.4+(3-2.5)2×0.4+(4-2.5)2×0.1=1.52×0.1+0.52×0.4+0.52×0.4+1.52×0.1=0.65,所以s1=.对于B,样本的平均数=1×0.4+2×0.1+3×0.1+
4×0.4=2.5,方差=(1-2.5)2×0.4+(2-2.5)2×0.1+(3-2.5)2×0.1+(4-2.5)2×0.4=1.52×0.4+0.52×0.1+0.52×0.1+1.52×0.4=1.85,所以s2=.对于C,样本的平均数=1×0.2+2×0.3+3×0.3+4×0.2=2.5,方差=(1-2.5)2×0.2+(2-2.5)2×0.3+(3-2.5)2×0.3+(4-2.5)2×0.2=1.52×0.2+0.52×0.3+0.52×0.3+1.52×0.2=1.05,所以s3=.对于D,样本的平均数=1×0.3+2×0.2+3×0.2+4×0.3=2.5,方差=(1-2.5)2×0.3+(2-2.5)2×0.2+(3-2.5)2×0.2+(4-2.5)2×0.3=1.52×0.3+0.52×0.2+0.52×0.2+1.52×0.3=1.45,所以s4=.所以B中的标准差最大.
5.C 因为样本数据x1,x2,…,xn的方差为0.01,D(aX)=a2D(X),所以样本数据10x1,10x2,…,10xn的方差为102×0.01=1,故选C.
6.B 设“一代”为x年,由题意得企业寿命的频率分布表为:
家族企业寿命 频率
[0,x) 54%
[x,2x) 28%
[2x,3x) 14%
[3x,4x] 4%
所以家族企业的平均寿命为0.54×0.5x+0.28×1.5x+0.14×2.5x+0.04×3.5x=26,解得x≈22.
二、多项选择题
7.CD 设样本数据x1,x2,…,xn的平均数、中位数、标准差、极差分别为,m,s,t,依题意,得新样本数据y1,y2,…,yn的平均数、中位数、标准差、极差分别为+c,m+c,s,t,因为c≠0,所以C,D正确,故选CD.
8.ABD 设2010年参加课外兴趣班的小学生总人数为a,则2020年参加课外兴趣班的小学生总人数是4a.由题中扇形图,知2010年和2020年参加音乐兴趣班的小学生人数分别为a×21%=0.21a,4a×21%=0.84a,故A正确;这10年间参加编程兴趣班的小学生人数变化量为4a×32%-a×5%=1.23a,参加语言表演兴趣班的小学生人数变化量为4a×20%-a×14%=0.66a,参加音乐兴趣班的小学生人数变化量为4a×21%-a×21%=0.63a,参加美术兴趣班的小学生人数变化量为4a×27%-a×60%=0.48a,因为1.23a>0.66a>0.63a>0.48a,所以这10年间参加编程兴趣班的小学生人数变化量最大,故B正确,C错误;根据题中扇形图中的比例分布,可知D正确.故选ABD.
9.AC 平均数、众数和中位数均刻画了样本数据的集中趋势,一般地,对数值型数据集中趋势的描述,可以用平均数和中位数,对分类型数据集中趋势的描述,可以用众数.方差、标准差和极差均是度量样本数据离散程度的.故选AC.
10.ABC 设2020年年总收入为W,则2021年年总收入为2W,观察扇形图可知:
A √ 2020年的甲系列产品收入为0.4W,2021年的甲系列产品收入为2W×20%=0.4W.
B √ 2020年的丁系列产品收入为0.15W,2021年的丁系列产品收入为2W×30%=0.6W,0.6W=4×0.15W.
C √ 2021年的丙和丁系列产品的收入之和为2W×(30%+25%)=1.1W>W.
D 2020年的乙和丙系列产品收入之和为(10%+20%)W=0.3W,2021年的乙和丙系列产品的收入之和为2W×(20%+25%)=0.9W,显然0.9W>2×0.3W.
三、解答题
11.解析(1)估计该林区这种树木平均一棵的根部横截面积=0.06,
估计该林区这种树木平均一棵的材积量=0.39.
(2)设该林区这种树木的总材积量的估计值为Y m3,由题意可知,该种树木的材积量与其根部横截面积近似成正比,所以,
所以Y==1 209,即该林区这种树木的总材积量的估计值为1 209 m3.
12.解析(1)由表格中的数据易得
×(-0.2+0.3+0+0.2-0.1-0.2+0+0.1+0.2-0.3)+10.0=10.0,
×(0.1+0.4+0.1+0+0.1+0.3+0.6+0.5+0.4+0.5)+10.0=10.3,
×[(9.7-10.0)2+2×(9.8-10.0)2+(9.9-10.0)2+2×(10.0-10.0)2+(10.1-10.0)2+2×(10.2-10.0)2+(10.3-10.0)2]=0.036,
×[(10.0-10.3)2+3×(10.1-10.3)2+(10.3-10.3)2+2×(10.4-10.3)2+2×(10.5-10.3)2+(10.6-10.3)2]=0.04.
(2)由(1)中数据可得=10.3-10.0=0.3,
2,
显然有>2成立,
所以认为新设备生产产品的该项指标的均值较旧设备有显著提高.
13.解析(1)由题意可知0.1=a×100,所以a=0.001.
(2)补全后的频率分布直方图如图所示,
阴影部分的面积为0.004×100+0.001×100=0.5.
14.解析(1)A公司员工月均工资的平均数为0.3×0.21+0.5×0.29+0.7×0.27+0.9×0.21+29×0.02=1.166(万元).
由题图1可知A公司员工月均工资在0.6万元以下的比例为0.21+0.29=0.5,
所以A公司员工月均工资的中位数约为0.6万元.
用中位数更能反映该公司普通员工的工资水平,理由如下:
因为平均数受每一个数据的影响,越离群的数据对平均数的影响越大,该公司少数员工的月收入很高,在这种情况下平均数并不能较好地反映普通员工的收入水平,而中位数不受少数极端数据的影响,可以较好地反映普通员工的收入水平.
(2)B公司员工月均工资的平均数为(0.3×0.375+0.5×0.750+0.7×2.750+0.9×1.000+1.1×0.125)×0.2=0.69(万元).
由题图2知,B公司员工月均工资在0.6万元以下的频率为(0.375+0.75)×0.2=0.225,
在0.8万元以下的频率为(0.375+0.750+2.750)×0.2=0.775.
设B公司员工月均工资的中位数为x万元,则(x-0.6)×2.750=0.5-0.225,得x=0.7.
小明应选择B公司应聘,理由如下:
B公司员工工资数据较为集中,月均工资的平均数和中位数均能反映该公司普通员工的平均收入水平,B公司员工月均工资平均数为0.69,中位数为0.7,均大于A公司员工月均工资的中位数0.62,所以以公司普通员工的工资水平作为决策依据,小明应该选B公司应聘.
15.解析(1)设从A,B两个地区抽取的用户人数分别为x,y,则,所以x=400,y=500-400=100.
所以该公司采用分层随机抽样的方法,从A,B两个地区抽取的用户人数分别为400和100.
(2)由频率分布直方图,知B地区抽取的用户中,对该产品评分不低于80分的用户频率为0.005×20=0.1,
所以估计B地区所有用户中,对该产品评分不低于80分的用户人数为0.1×10 000=1 000.
(3)μ0>.理由如下:
由(1)知μ0=,
所以μ0-.
又μ1=30×0.005×20+50×0.015×20+70×0.020×20+90×0.010×20=64,
μ2=30×0.015×20+50×0.010×20+70×0.020×20+90×0.005×20=56,
所以μ1>μ2,所以>0,所以μ0>.
16.解析(1)根据频率分布直方图,得(0.01+0.013+a+0.007+0.002)×20=1,
解得a=0.018.
由频率分布直方图可估计平均数为
10×0.01×20+30×0.013×20+50×0.018×20+70×0.007×20+90×0.002×20=41.2,
所以估计该市年龄100岁及以下居民的平均年龄为41.2岁.
(2)被调查的100名居民中,年龄处在[0,20),[20,40),[40,60),[60,80),[80,100]的人数分别为20,26,36,14,4.
由表格,得这100名居民对防骗知识的知晓率为×(20×0.34+26×0.45+36×0.54+14×0.65+4×0.74)=50%,
所以估计该市年龄100岁及以下居民对防骗知识的知晓率为50%.
(3)原因分析:
①样本数据过少,不能很好地反映总体数据的特征;
②调查的人数中年龄在[60,100]的只有18人,也许这部分人刚好对防骗知识的知晓率高,从而导致调查结果不能很好地代表实际情况.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
