第九章 统计全章综合检测 -2022-2023学年高一下学期数学人教A版(2019)必修第二册(含答案)
文档属性
| 名称 | 第九章 统计全章综合检测 -2022-2023学年高一下学期数学人教A版(2019)必修第二册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 446.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 00:00:00 | ||
图片预览



文档简介
《第九章 统计》全章综合检测
班级: 姓名: 成绩:
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.①一次数学考试中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关情况;②运动会的工作人员从参加4×100 m接力赛的6支队伍中抽取1支接受采访.针对这两件事,恰当的抽样方法分别为( )
A.分层随机抽样,简单随机抽样
B.简单随机抽样,简单随机抽样
C.简单随机抽样,分层随机抽样
D.分层随机抽样,分层随机抽样
2.[2022安徽宿州十三所重点中学高一上期末]某校为调查学生对学校“延时服务”的满意率,想从全市3个分校区按学生数用分层随机抽样的方法抽取一个容量为n的样本.已知3个校区学生数之比为2∶3∶5,如果最多的一个校区抽出的个体数是60,那么这个样本的容量为( )
A.96 B.120 C.180 D.240
3.一组数据从小到大排列依次为3,5,6,7,8,9,x,12,13,13,且该组数据70%分位数不超过11,则x的取值范围是( )
A.[9,12] B.(9,11] C.(9,10) D.[9,10]
4.中国农历的“二十四节气”是中华民族的智慧与传统文化的结晶,2016年11月30日,“二十四节气”正式被联合国教科文组织列入人类非物质文化遗产名录,也被誉为“中国的第五大发明”.某小学三年级共有学生500名,随机抽查100名学生并提问“二十四节气”歌,只能说出两句的有45人,能说出三句及其以上的有32人,据此估计该校三年级的500名学生中,对“二十四节气”歌只能说出一句或一句也说不出的大约有( )
A.69人 B.84人 C.108人 D.115人
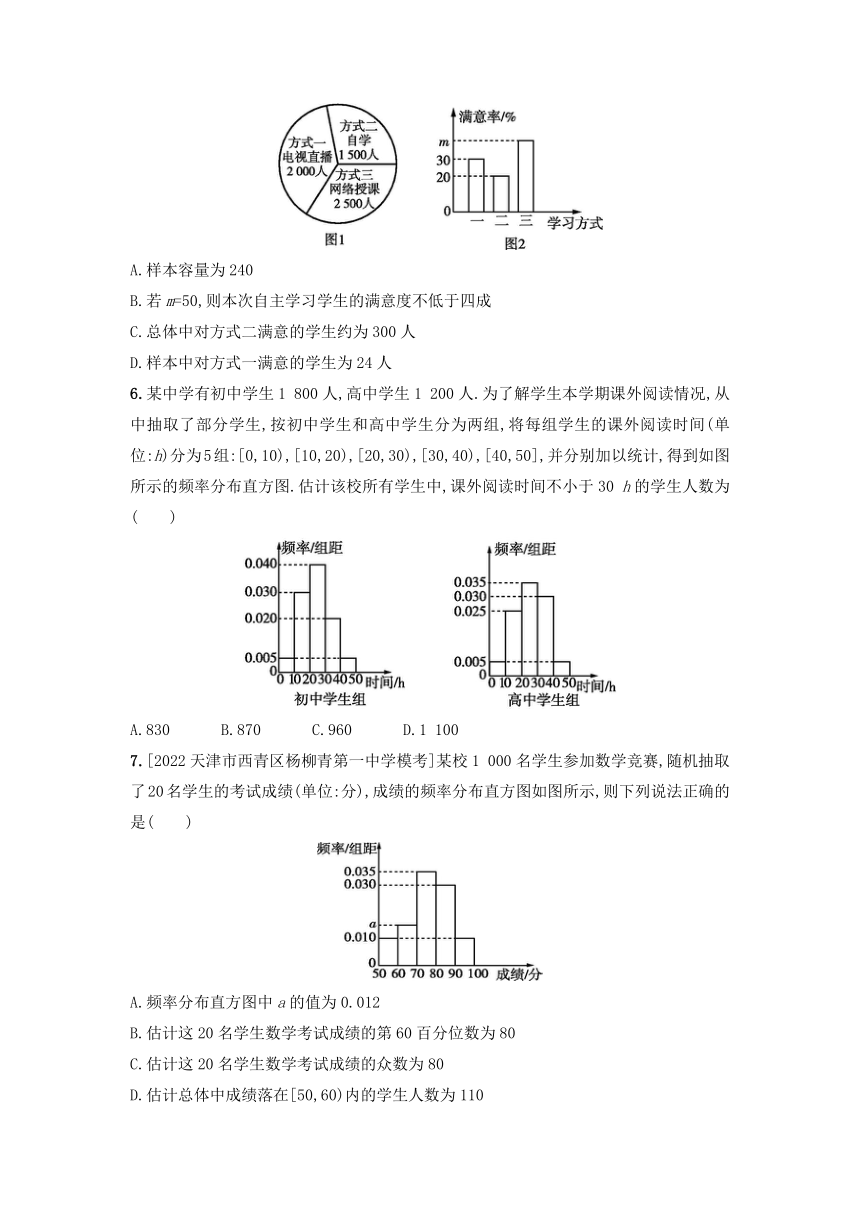
5.[2022广东五校高一下期末联考]五月初,受疫情影响线下课暂停,某校组织学生居家通过三种方式自主学习,每种学习方式人数分布如图1所示,解封后为了解学生对这三种学习方式的满意程度,利用分层随机抽样的方法抽取4%的同学进行满意率调查,得到的数据如图2所示.则下列说法中不正确的是( )
A.样本容量为240
B.若m=50,则本次自主学习学生的满意度不低于四成
C.总体中对方式二满意的学生约为300人
D.样本中对方式一满意的学生为24人
6.某中学有初中学生1 800人,高中学生1 200人.为了解学生本学期课外阅读情况,从中抽取了部分学生,按初中学生和高中学生分为两组,将每组学生的课外阅读时间(单位:h)分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],并分别加以统计,得到如图所示的频率分布直方图.估计该校所有学生中,课外阅读时间不小于30 h的学生人数为( )
A.830 B.870 C.960 D.1 100
7.[2022天津市西青区杨柳青第一中学模考]某校1 000名学生参加数学竞赛,随机抽取了20名学生的考试成绩(单位:分),成绩的频率分布直方图如图所示,则下列说法正确的是( )
A.频率分布直方图中a的值为0.012
B.估计这20名学生数学考试成绩的第60百分位数为80
C.估计这20名学生数学考试成绩的众数为80
D.估计总体中成绩落在[50,60)内的学生人数为110
8.[2022山西长治二中高一下期末]四名同学各掷骰子7次,分别记录每次骰子出现的点数,根据4名同学的统计结果,可以判断出一定没有出现点数6的是( )
A.平均数为4,中位数为4
B.中位数为4,众数为3
C.平均数为3,方差为1
D.中位数为3,方差为
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.[2022河北邢台高一段考]已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数与众数的和是中位数的2倍,则丢失的数据可能是( )
A.-10 B.4 C.12 D.20
10.[2022湖南长沙长郡中学高一下期末]2022年北京冬奥会成功举办.中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领相关户外用品行业市场增长.下面是2015年至2021年中国雪场滑雪人次与同比增长率(与上一年相比)的统计情况,则下面结论中正确的是( )
A.2016年至2021年,中国雪场滑雪人次的同比增长率逐年下降
B.2016年至2021年,中国雪场滑雪人次逐年增加
C.2016年与2021年,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等
D.2016年至2021年,中国雪场滑雪人次增长率为118.9%
11.某班有50名学生,其中男生30名,随机询问了该班5名男生和5名女生在某次数学测验中的成绩.5名男生的成绩分别为86,94,88,92,90,5名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )
A.这种抽样方法是简单随机抽样
B.这5名男生成绩的中位数小于这5名女生成绩的中位数
C.这5名男生成绩的方差大于这5名女生成绩的方差
D.该班男生成绩的平均数小于该班女生成绩的平均数
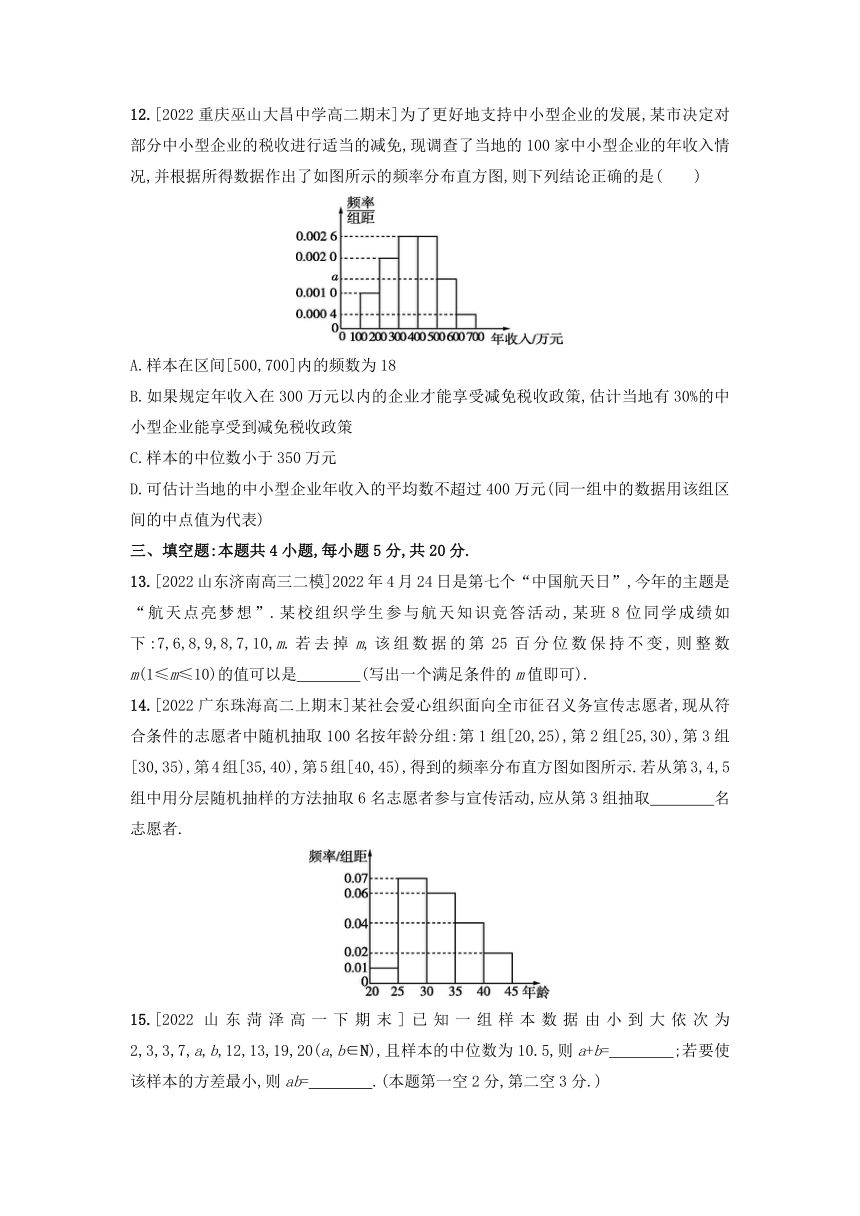
12.[2022重庆巫山大昌中学高二期末]为了更好地支持中小型企业的发展,某市决定对部分中小型企业的税收进行适当的减免,现调查了当地的100家中小型企业的年收入情况,并根据所得数据作出了如图所示的频率分布直方图,则下列结论正确的是( )
A.样本在区间[500,700]内的频数为18
B.如果规定年收入在300万元以内的企业才能享受减免税收政策,估计当地有30%的中小型企业能享受到减免税收政策
C.样本的中位数小于350万元
D.可估计当地的中小型企业年收入的平均数不超过400万元(同一组中的数据用该组区间的中点值为代表)
三、填空题:本题共4小题,每小题5分,共20分.
13.[2022山东济南高三二模]2022年4月24日是第七个“中国航天日”,今年的主题是“航天点亮梦想”.某校组织学生参与航天知识竞答活动,某班8位同学成绩如下:7,6,8,9,8,7,10,m.若去掉m,该组数据的第25百分位数保持不变,则整数m(1≤m≤10)的值可以是 (写出一个满足条件的m值即可).
14.[2022广东珠海高二上期末]某社会爱心组织面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.若从第3,4,5组中用分层随机抽样的方法抽取6名志愿者参与宣传活动,应从第3组抽取 名志愿者.
15.[2022山东菏泽高一下期末]已知一组样本数据由小到大依次为2,3,3,7,a,b,12,13,19,20(a,b∈N),且样本的中位数为10.5,则a+b= ;若要使该样本的方差最小,则ab= .(本题第一空2分,第二空3分.)
16.一组数据由10个数组成,将其中一个数由4改为1,另一个数由6改为9,其余数不变,得到新的10个数,则新的一组数的方差相比原先一组数的方差的增加值为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)某企业计划引进A,B两种设备对某产品进行进一步的加工.A设备每台每天可以加工30件,每天维护费用为500元/台;B设备每台每天可以加工4件,每天维护费用为80元/台.该企业现有两种购置方法:
方法一,购买100台A设备和800台B设备;
方法二,购买200台A设备和450台B设备.
假设进一步加工后每件产品可以增加25元的收入.
该企业随机统计了100天中该产品每天的生产件数,得到如下的频数分布表.
分组 [5 500,6 500) [6 500,7 500) [7 500,8 500) [8 500,9 500]
频数 20 30 40 10
以抽取的这100天中该产品的生产情况(同一组中的数据用该组区间的中点值代表)为基础,试选择一种购置方法,求该方法中使用A,B两种设备后的日增加的利润的均值.(日增加的利润=日增加的收入-日维护费用)
注:如果选择两种购置方法分别解答,按第一个解答计分.
18.(12分)[2022安徽芜湖高一期末]某校新入学的500名高一学生订购校服的尺码条形图如图所示.
(1)请根据同学订购校服的尺码条形图估算该校高一同学的平均身高;
(2)从入学体检可知该校高一男同学平均身高为172 cm,女同学平均身高为164 cm,请根据体检数据计算出该校高一学生平均身高,并分析(1)中的估算值与由体检数据得出的平均值存在差异的原因.
19.(12分)[2022福建福州八县高一下期末联考]某大学艺术专业400名学生参加某次测评,根据男、女学生人数比例,使用分层随机抽样的方法从中随机抽取了100名学生,记录学生的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图.
(1)根据频率分布直方图,判断样本中的平均数与中位数的大小关系,并简述理由;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)上的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等,试估计总体中男生和女生人数的比例.
20.(12分)[2022山东潍坊高一期末]某大学为了解学生对A,B两家餐厅的满意度情况,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行满意指数打分(满意指数是指学生对餐厅满意度情况的打分,分数设置为2~10分).根据打分结果按,,,分组,得到如图所示的频率分布直方图,其中B餐厅满意指数在内的有30人.
(1)求B餐厅满意指数频率分布直方图中a,b的值.
(2)利用样本估计总体的思想,估计A餐厅满意指数和B餐厅满意指数的平均数及方差(同一组中的数据用该组区间中点值作代表).
(3)如果一名新来的同学打算从A,B两家餐厅中选择一个用餐,你建议他选择哪个餐厅 说明理由.
21.(12分)[2022湖南张家界高一下期末联考]某市工会组织举行“红心向党”职工歌咏比赛,分初赛、复赛和决赛三个环节,全市职工踊跃参与初赛,通过各单位的初选,最终有2 000名选手进入复赛,经统计,其年龄的频率分布直方图如图所示.
(1)求直方图中x的值,并估计复赛选手年龄的平均值(同一组中的数据用该区间的中点值作代表,结果保留一位小数).
(2)根据频率分布直方图估计复赛选手年龄的第75百分位数.
(3)决赛由8名专业评审、10名媒体评审和12名大众评审分别打分,打分均采用10分制.已知某选手专业得分的平均数和方差分别为=8.4,=0.015,媒体得分的平均数和方差分别为=8.8,=0.054,大众得分的平均数和方差分别为=9.4,=0.064,将这30名评审的平均分作为最终得分,请估计该选手的最终得分和方差(结果保留三位小数).
22.(12分)[2022江苏无锡梅村高级中学高一下期中]中国独有的文书工具,即笔、墨、纸、砚,有文房四宝之名,起源于南北朝时期.其中宣纸“始于唐代,产于泾县”,因唐代泾县隶属宣州管理,故因地得名宣纸,宣纸按质量等级分为:正牌(优等品)、副牌(合格品)、废品三等.某公司生产的宣纸为纯手工制作,年产宣纸10 000刀(1刀=100张), 该公司按照某种质量指标x给宣纸确定等级如表所示:
x的范围 (44,48]∪(52,56] (48,52] [0,44]∪(56,60]
质量等级 副牌 正牌 废品
在该公司所生产的宣纸中随机抽取了一刀进行检验,得到频率分布直方图如图所示,已知每张正牌宣纸的利润为15元,副牌宣纸的利润为8元,废品的利润为-20元.
(1)试估计该公司的年利润.
(2)市场上有一种售价为100万元的机器可以改进宣纸的生产工艺,但这种机器的使用寿命为一年,只能提高宣纸的质量,不能增加宣纸的年产量.据调查这种机器生产的宣纸的质量指标x如表所示:
其中为质量指标x的平均值,但是由于人们对传统手工工艺的认可,改进后的正牌和副牌宣纸的利润都将下降3元/张,该公司是否应该购买这种机器 请你为该公司提出合理建议,并说明理由.(同一组的数据用该组区间的中点值作代表)
x的范围 (-2,+2) (-6,+6)
频率 0.682 7 0.954 5
参考答案
一、单项选择题
1.A ①中,在不同分数段内的同学的考试成绩有明显的差异,用分层随机抽样比较恰当;②中,总体包含的个体较少,用简单随机抽样比较恰当.
2.B 设样本容量为n,因为3个校区学生数之比为2∶3∶5,最多的一个校区抽出的个体数是60,所以n×=60,解得n=120.故选B.
3.D 因为10×70%=7,所以70%分位数为,所以解得9≤x≤10.
4.D 由题意知,随机抽查的100人中只能说出一句或一句也说不出的同学有100-45-32=23(人),故只能说出一句或一句也说不出的学生占的比例为,故只能说出一句或一句也说不出的学生大约有500×=115(人).
5.B 对于A,由扇形图可得总人数为1 500+2 000+2 500=6 000,故样本容量为6 000×4%=240,故A说法正确;对于B,当m=50时,满意的人数为2 000×0.3+1 500×0.2+2 500×0.5=2 150,故满意度为=0.4,故B说法错误;对于C,总体中对方式二满意的学生人数约为1 500×0.2=300,故C说法正确;对于D,样本中对方式一满意的学生人数为2 000×4%×
6.B 因为初中学生中课外阅读时间不小于30 h的频率为(0.02+0.005)×10=0.25,所以该校所有的初中学生中,课外阅读时间不小于30 h的学生人数约为0.25×1 800=450.同理,高中学生中课外阅读时间不小于30 h的频率为(0.03+0.005)×10=0.35,故该校所有的高中学生中,课外阅读时间不小于30 h的学生人数约为0.35×1 200=420.所以该校所有学生中,课外阅读时间不小于30 h的学生人数约为450+420=870.
7.B
A 由(0.01+a+0.035+0.03+0.01)×10=1,可得a=0.015.
B √ 前三个矩形的面积和为0.1+0.15+0.35=0.6,所以估计这20名学生数学考试成绩的第60百分位数为80.
C 估计这20名学生数学考试成绩的众数为=75.
D 这20名学生数学考试成绩落在[50,60)内的学生人数为20×0.1=2,则估计总体中成绩落在[50,60)内的学生人数为×2=100.
8.C
A 当投掷骰子出现结果为1,2,3,4,6,6,6时,满足平均数为4,中位数为4,可以出现点数6.
B 当投掷骰子出现结果为3,3,3,4,4,5,6时,满足中位数为4,众数为3,可以出现点数6.
C 若平均数为3,且出现6点,则方差s2>(6-3)2=>1,所以平均数为3,方差为1时,一定没有出现点数6.
D 当投掷骰子出现结果为2,2,3,3,6,6,6时,满足中位数为3,平均数为(2+2+3+3+6+6+6)=4,方差为s2=[(2-4)2+(2-4)2+(3-4)2+(3-4)2+(6-4)2+(6-4)2+(6-4)2]=,可以出现点数6.
由以上分析知选C.
二、多项选择题
9.AB 设丢失的数据为x,则这七个数据的平均数为,众数是3.因为这组数据的平均数与众数的和是中位数的2倍,所以若x≤3,则中位数为3,此时+3=2×3,解得x=-10;若310.BD
A 2016年至2018年,中国雪场滑雪人次的同比增长率逐年增加,2018年至2021年同比增长率逐年下降.
B √ 由条形图可知,2016年至2021年,中国雪场滑雪人次逐年增加.
C 由统计图可知,2016年与2021年,中国雪场滑雪人次的同比增长率近似相等,但是2015年滑雪人次为800万,2020年滑雪人次为1750万,同比增长基数差距大,同比增长人数不相等.
D √ 由统计图可知,2016年至2021年,中国雪场滑雪人次的增长率约为×100%≈118.9%.
11.ABC 根据抽样方法,可知这种抽样方法是简单随机抽样,A正确;易知这5名男生成绩的中位数是90,这5名女生成绩的中位数是93,故B正确;5名男生成绩的平均数为(86+94+88+92+90)÷5=90,方差为[(86-90)2+(94-90)2+(88-90)2+(92-90)2+(90-90)2]=8,5名女生成绩的平均数为(88+93+93+88+93)÷5=91,方差为[(88-91)2+(93-91)2+(93-91)2+(88-91)2+(93-91)2]=6,故C正确;由于该班男生成绩的平均数与该班女生成绩的平均数不一定是样本的平均数,故D错误.
12. ABD
A √ 由题图可得100×(0.001+0.002+0.002 6×2+a+0.000 4)=1,解得a=0.001 4,故样本在区间[500,700]内的频数为100×(0.001 4+0.000 4)×100=18.
B √ 年收入在300万元以内的企业的频率为100×(0.001+0.002)=0.3.
C 100×(0.001+0.002+0.002 6)=0.56>0.5,则中位数在[300,400)内,设为x,则(x-300)×0.002 6=0.5-0.3,得x≈377>350.
D √ 样本年收入的平均数为100×(150×0.001+250×0.002+350×0.002 6+450×0.002 6+550×0.001 4+650×0.000 4)=376(万元),则估计当地的中小型企业年收入的平均数为376万元.
三、填空题
13.7或8或9或10(填上述4个数中任意一个均可) 解析7,6,8,9,8,7,10,m,若去掉m,该组数据从小到大排列为:6,7,7,8,8,9,10,则7×0.25=1.75,故第25百分位数为第二个数即7,所以7,6,8,9,8,7,10,m的第25百分位数为7,而8×0.25=2,所以7为将7,6,8,9,8,7,10,m从小到大排列后的第二个数与第三个数的平均数,所以m(1≤m≤10)的值可以是7或8或9或10.(注:写出一个满足题意的答案即可.)
14.3 解析第3组的人数为100×5×0.06=30,第4组的人数为100×5×0.04=20,第5组的人数为100×5×0.02=10,所以这三组共有60名志愿者,所以利用分层随机抽样的方法在60名志愿者中抽取6名志愿者,第3组应抽取6×=3(名).
15.21 110 解析因为样本数据由小到大依次为2,3,3,7,a,b,12,13,19,20(a,b∈N),且样本的中位数为10.5,所以=10.5,即a+b=21,所以样本的平均数为=10.要使样本方差最小,即(a-10)2+(b-10)2最小,又(a-10)2+(b-10)2=(21-b-10)2+(b-10)2=(11-b)2+(b-10)2=2b2-42b+221=2(b-)2+,且b∈N,所以当b=11或b=10时,(a-10)2+(b-10)2取得最小值.又a+b=21,所以a=11,b=10或a=10,b=11,所以ab=110.
16.3 解析由题意,一个数由4改为1,另一个数由6改为9,其余数不变,可得该组数据的平均数不变,设没有改变的8个数分别为x1,x2,…,x8,原先一组数据的方差为s2=[(x1-)2+(x2-)2+…+(x8-)2+(4-)2+],新数据的方差为[(x1-)2+(x2-)2+…+(x8-)2+(1-)2+(9-)2],所以-s2=[(1-)2+(9-)2-(4-)2-(6-)2]=(1-2 +81-18-16+8-36+12)=3,所以新的一组数据的方差相比原先一组数据的方差的增加值为3.
四、解答题
17.解析方案一 选择方法一.
同一组数据用该组区间的中点值为代表,得到这100天中该产品每天生产件数的频数分布表如下:
件数 6 000 7 000 8 000 9 000
频数 20 30 40 10
(2分)
使用100台A设备和800台B设备每天可进一步加工的件数为30×100+4×800=6 200,则这100天中该产品每天进一步加工件数的频数分布表如下:
进一步加工的件数 6 000 6 200
频数 20 80
(6分)
所以使用A,B设备进一步加工后的日增加的利润的均值为25×-500×100-80×800=40 000(元).(10分)
方案二 选择方法二.
同一组数据用该组区间的中点值为代表,得到这100天中该产品每天生产件数的频数分布表如下:
件数 6 000 7 000 8 000 9 000
频数 20 30 40 10
(2分)
使用200台A设备和450台B设备每天可进一步加工的件数为30×200+4×450=7 800,则这100天中该产品每天进一步加工件数的频数分布表如下:
进一步加工的件数 6 000 7 000 7 800
频数 20 30 50
(6分)
所以使用A,B设备进一步加工后的日增加的利润的均值为
25×-500×200-80×450=44 000(元).(10分)
18.解析(1)全体高一同学平均身高的估计值为160×+165×+170×+175×+180×+185×+190×=174.2(cm).(5分)
(2)由题图可得,高一男同学的总人数为300,女同学的总人数为200,故由体检数据计算出该校高一学生平均身高为172×+164×=168.8(cm).(8分)
存在差异的原因,参考答案(酌情给分,言之有理即可):
①订购校服时,大多数学生会选择高于自身身高的尺码校服,如身高172 cm的同学,一般会订购175 cm尺码的校服,甚至更大尺码;
②部分同学因考虑舒适或继续长高会订购更大尺码;
③体型偏胖的学生一般会订购比自己身高大的尺码;
④订购校服和体检时,都可能出现误差.(12分)
19.解析(1)平均数<中位数.理由:直方图在左边“拖尾”,和中位数相比,平均数总是在“长尾巴”那边.(2分)
(2)依题意,[20,30),[30,40)两个组的频率之和为=0.05,[50,60),[60,70),[70,80),[80,90]四个组的频率之和为0.1+0.2+0.4+0.2=0.9,
则[40,50)对应的频率为1-0.05-0.9=0.05.
故总体中分数在区间[40,50)上的人数大约为400×0.05=20.(7分)
(3)依题意,样本中分数不小于70的频率为0.4+0.2=0.6,则样本中分数不小于70的人数为100×0.6=60,其中男女生人数都为30,即样本中男生人数为60,女生人数为40,故男生和女生人数的比例为60∶40=3∶2.
所以由样本估计总体可得,总体中男生和女生人数的比例大约为3∶2.(12分)
20.解析(1)因为B餐厅满意指数在内的有30人,所以2×b=,解得b=0.15.
又0.15×2+a×2+0.2×2+0.05×2=1,解得a=0.1.(3分)
(2)设A餐厅满意指数的平均数和方差分别为,,B餐厅满意指数的平均数和方差分别为,,则有=3×0.1+5×0.3+7×0.4+9×0.2=6.4,=(3-6.4)2×0.1+(5-6.4)2×0.3+(7-6.4)2×0.4+(9-6.4)2×0.2=3.24,
=3×0.3+5×0.2+7×0.4+9×0.1=5.6,=(3-5.6)2×0.3+(5-5.6)2×0.2+(7-5.6)2×0.4+(9-5.6)2×0.1=4.04.
综上,A餐厅满意指数的平均数和方差分别为6.4,3.24;
B餐厅满意指数的平均数和方差分别5.6,4.04.(8分)
(3)答案一 A餐厅满意指数的平均数为6.4,方差为3.24,B餐厅满意指数的平均数为5.6,方差为4.04,因为6.4>5.6,3.24<4.04,所以推荐A餐厅.(12分)
答案二 A餐厅满意指数在[2,6)的频率为0.4,在[6,10]的频率为0.6,B餐厅满意指数在[2,6)和[6,10]的频率都为0.5,所以推荐A餐厅.
(答案不唯一,言之有理即可.)(12分)
21.解析(1)由题意,(0.01+0.015+0.020+2x+0.030+0.035+0.040)×5=1,解得x=0.025.(2分)
=(22.5×0.010+27.5×0.025+32.5×0.035+37.5×0.040+42.5×0.030+47.5×0.025+52.5×0.020+57.5×0.015)×5≈39.6(岁).(4分)
(2)通过计算知第75百分位数落在[45,50)区间内,设为t,则(0.010+0.025+0.035+0.040+0.030)×5+(t-45)×0.025=0.75,
解得t=47,即第75百分位数为47.(7分)
(3)设该名选手最终的平均分为,最终方差为s2,
则(8.4×8+8.8×10+9.4×12)≈8.933(分),(9分)
s2={8[]+12[+()2]}={8[0.015+(8.4-8.933)2]+10[0.054+(8.8-8.933)2]+12[0.064+(9.4-8.933)2]}≈0.216.
估计该选手最终得分为8.933分,其得分方差为0.216.(12分)
22.解析(1)由频率分布直方图得,一刀宣纸有正牌100×0.1×4=40(张),有副牌100×0.05×4×2=40(张),有废品100×0.025×4×2=20(张),
所以该公司一刀宣纸的利润的估计值为40×15+40×8-20×20=520(元),
所以估计该公司的年利润为520万元.(4分)
(2)由频率分布直方图得,
=42×0.025×4+46×0.05×4+50×0.1×4+54×0.05×4+58×0.025×4=50.(6分)
由表格数据可得一刀宣纸中正牌的张数估计为100×0.682 7=68.27,
废品的张数估计为100×(1-0.954 5)=4.55,
副牌的张数估计为100×(0.954 5-0.682 7)=27.18,
所以一刀宣纸的利润为68.27×12+27.18×5-4.55×20=864.14(元),(9分)
10 000刀宣纸的利润为10 000×864.14=8 641 400(元)=864.14(万元)
所以购买这种机器后该公司的利润为:864.14-100=764.14(万元),
因为764.14>520,所以建议该公司购买这种机器.(12分)
班级: 姓名: 成绩:
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.①一次数学考试中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关情况;②运动会的工作人员从参加4×100 m接力赛的6支队伍中抽取1支接受采访.针对这两件事,恰当的抽样方法分别为( )
A.分层随机抽样,简单随机抽样
B.简单随机抽样,简单随机抽样
C.简单随机抽样,分层随机抽样
D.分层随机抽样,分层随机抽样
2.[2022安徽宿州十三所重点中学高一上期末]某校为调查学生对学校“延时服务”的满意率,想从全市3个分校区按学生数用分层随机抽样的方法抽取一个容量为n的样本.已知3个校区学生数之比为2∶3∶5,如果最多的一个校区抽出的个体数是60,那么这个样本的容量为( )
A.96 B.120 C.180 D.240
3.一组数据从小到大排列依次为3,5,6,7,8,9,x,12,13,13,且该组数据70%分位数不超过11,则x的取值范围是( )
A.[9,12] B.(9,11] C.(9,10) D.[9,10]
4.中国农历的“二十四节气”是中华民族的智慧与传统文化的结晶,2016年11月30日,“二十四节气”正式被联合国教科文组织列入人类非物质文化遗产名录,也被誉为“中国的第五大发明”.某小学三年级共有学生500名,随机抽查100名学生并提问“二十四节气”歌,只能说出两句的有45人,能说出三句及其以上的有32人,据此估计该校三年级的500名学生中,对“二十四节气”歌只能说出一句或一句也说不出的大约有( )
A.69人 B.84人 C.108人 D.115人
5.[2022广东五校高一下期末联考]五月初,受疫情影响线下课暂停,某校组织学生居家通过三种方式自主学习,每种学习方式人数分布如图1所示,解封后为了解学生对这三种学习方式的满意程度,利用分层随机抽样的方法抽取4%的同学进行满意率调查,得到的数据如图2所示.则下列说法中不正确的是( )
A.样本容量为240
B.若m=50,则本次自主学习学生的满意度不低于四成
C.总体中对方式二满意的学生约为300人
D.样本中对方式一满意的学生为24人
6.某中学有初中学生1 800人,高中学生1 200人.为了解学生本学期课外阅读情况,从中抽取了部分学生,按初中学生和高中学生分为两组,将每组学生的课外阅读时间(单位:h)分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],并分别加以统计,得到如图所示的频率分布直方图.估计该校所有学生中,课外阅读时间不小于30 h的学生人数为( )
A.830 B.870 C.960 D.1 100
7.[2022天津市西青区杨柳青第一中学模考]某校1 000名学生参加数学竞赛,随机抽取了20名学生的考试成绩(单位:分),成绩的频率分布直方图如图所示,则下列说法正确的是( )
A.频率分布直方图中a的值为0.012
B.估计这20名学生数学考试成绩的第60百分位数为80
C.估计这20名学生数学考试成绩的众数为80
D.估计总体中成绩落在[50,60)内的学生人数为110
8.[2022山西长治二中高一下期末]四名同学各掷骰子7次,分别记录每次骰子出现的点数,根据4名同学的统计结果,可以判断出一定没有出现点数6的是( )
A.平均数为4,中位数为4
B.中位数为4,众数为3
C.平均数为3,方差为1
D.中位数为3,方差为
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.[2022河北邢台高一段考]已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数与众数的和是中位数的2倍,则丢失的数据可能是( )
A.-10 B.4 C.12 D.20
10.[2022湖南长沙长郡中学高一下期末]2022年北京冬奥会成功举办.中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领相关户外用品行业市场增长.下面是2015年至2021年中国雪场滑雪人次与同比增长率(与上一年相比)的统计情况,则下面结论中正确的是( )
A.2016年至2021年,中国雪场滑雪人次的同比增长率逐年下降
B.2016年至2021年,中国雪场滑雪人次逐年增加
C.2016年与2021年,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等
D.2016年至2021年,中国雪场滑雪人次增长率为118.9%
11.某班有50名学生,其中男生30名,随机询问了该班5名男生和5名女生在某次数学测验中的成绩.5名男生的成绩分别为86,94,88,92,90,5名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )
A.这种抽样方法是简单随机抽样
B.这5名男生成绩的中位数小于这5名女生成绩的中位数
C.这5名男生成绩的方差大于这5名女生成绩的方差
D.该班男生成绩的平均数小于该班女生成绩的平均数
12.[2022重庆巫山大昌中学高二期末]为了更好地支持中小型企业的发展,某市决定对部分中小型企业的税收进行适当的减免,现调查了当地的100家中小型企业的年收入情况,并根据所得数据作出了如图所示的频率分布直方图,则下列结论正确的是( )
A.样本在区间[500,700]内的频数为18
B.如果规定年收入在300万元以内的企业才能享受减免税收政策,估计当地有30%的中小型企业能享受到减免税收政策
C.样本的中位数小于350万元
D.可估计当地的中小型企业年收入的平均数不超过400万元(同一组中的数据用该组区间的中点值为代表)
三、填空题:本题共4小题,每小题5分,共20分.
13.[2022山东济南高三二模]2022年4月24日是第七个“中国航天日”,今年的主题是“航天点亮梦想”.某校组织学生参与航天知识竞答活动,某班8位同学成绩如下:7,6,8,9,8,7,10,m.若去掉m,该组数据的第25百分位数保持不变,则整数m(1≤m≤10)的值可以是 (写出一个满足条件的m值即可).
14.[2022广东珠海高二上期末]某社会爱心组织面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.若从第3,4,5组中用分层随机抽样的方法抽取6名志愿者参与宣传活动,应从第3组抽取 名志愿者.
15.[2022山东菏泽高一下期末]已知一组样本数据由小到大依次为2,3,3,7,a,b,12,13,19,20(a,b∈N),且样本的中位数为10.5,则a+b= ;若要使该样本的方差最小,则ab= .(本题第一空2分,第二空3分.)
16.一组数据由10个数组成,将其中一个数由4改为1,另一个数由6改为9,其余数不变,得到新的10个数,则新的一组数的方差相比原先一组数的方差的增加值为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)某企业计划引进A,B两种设备对某产品进行进一步的加工.A设备每台每天可以加工30件,每天维护费用为500元/台;B设备每台每天可以加工4件,每天维护费用为80元/台.该企业现有两种购置方法:
方法一,购买100台A设备和800台B设备;
方法二,购买200台A设备和450台B设备.
假设进一步加工后每件产品可以增加25元的收入.
该企业随机统计了100天中该产品每天的生产件数,得到如下的频数分布表.
分组 [5 500,6 500) [6 500,7 500) [7 500,8 500) [8 500,9 500]
频数 20 30 40 10
以抽取的这100天中该产品的生产情况(同一组中的数据用该组区间的中点值代表)为基础,试选择一种购置方法,求该方法中使用A,B两种设备后的日增加的利润的均值.(日增加的利润=日增加的收入-日维护费用)
注:如果选择两种购置方法分别解答,按第一个解答计分.
18.(12分)[2022安徽芜湖高一期末]某校新入学的500名高一学生订购校服的尺码条形图如图所示.
(1)请根据同学订购校服的尺码条形图估算该校高一同学的平均身高;
(2)从入学体检可知该校高一男同学平均身高为172 cm,女同学平均身高为164 cm,请根据体检数据计算出该校高一学生平均身高,并分析(1)中的估算值与由体检数据得出的平均值存在差异的原因.
19.(12分)[2022福建福州八县高一下期末联考]某大学艺术专业400名学生参加某次测评,根据男、女学生人数比例,使用分层随机抽样的方法从中随机抽取了100名学生,记录学生的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图.
(1)根据频率分布直方图,判断样本中的平均数与中位数的大小关系,并简述理由;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)上的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等,试估计总体中男生和女生人数的比例.
20.(12分)[2022山东潍坊高一期末]某大学为了解学生对A,B两家餐厅的满意度情况,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行满意指数打分(满意指数是指学生对餐厅满意度情况的打分,分数设置为2~10分).根据打分结果按,,,分组,得到如图所示的频率分布直方图,其中B餐厅满意指数在内的有30人.
(1)求B餐厅满意指数频率分布直方图中a,b的值.
(2)利用样本估计总体的思想,估计A餐厅满意指数和B餐厅满意指数的平均数及方差(同一组中的数据用该组区间中点值作代表).
(3)如果一名新来的同学打算从A,B两家餐厅中选择一个用餐,你建议他选择哪个餐厅 说明理由.
21.(12分)[2022湖南张家界高一下期末联考]某市工会组织举行“红心向党”职工歌咏比赛,分初赛、复赛和决赛三个环节,全市职工踊跃参与初赛,通过各单位的初选,最终有2 000名选手进入复赛,经统计,其年龄的频率分布直方图如图所示.
(1)求直方图中x的值,并估计复赛选手年龄的平均值(同一组中的数据用该区间的中点值作代表,结果保留一位小数).
(2)根据频率分布直方图估计复赛选手年龄的第75百分位数.
(3)决赛由8名专业评审、10名媒体评审和12名大众评审分别打分,打分均采用10分制.已知某选手专业得分的平均数和方差分别为=8.4,=0.015,媒体得分的平均数和方差分别为=8.8,=0.054,大众得分的平均数和方差分别为=9.4,=0.064,将这30名评审的平均分作为最终得分,请估计该选手的最终得分和方差(结果保留三位小数).
22.(12分)[2022江苏无锡梅村高级中学高一下期中]中国独有的文书工具,即笔、墨、纸、砚,有文房四宝之名,起源于南北朝时期.其中宣纸“始于唐代,产于泾县”,因唐代泾县隶属宣州管理,故因地得名宣纸,宣纸按质量等级分为:正牌(优等品)、副牌(合格品)、废品三等.某公司生产的宣纸为纯手工制作,年产宣纸10 000刀(1刀=100张), 该公司按照某种质量指标x给宣纸确定等级如表所示:
x的范围 (44,48]∪(52,56] (48,52] [0,44]∪(56,60]
质量等级 副牌 正牌 废品
在该公司所生产的宣纸中随机抽取了一刀进行检验,得到频率分布直方图如图所示,已知每张正牌宣纸的利润为15元,副牌宣纸的利润为8元,废品的利润为-20元.
(1)试估计该公司的年利润.
(2)市场上有一种售价为100万元的机器可以改进宣纸的生产工艺,但这种机器的使用寿命为一年,只能提高宣纸的质量,不能增加宣纸的年产量.据调查这种机器生产的宣纸的质量指标x如表所示:
其中为质量指标x的平均值,但是由于人们对传统手工工艺的认可,改进后的正牌和副牌宣纸的利润都将下降3元/张,该公司是否应该购买这种机器 请你为该公司提出合理建议,并说明理由.(同一组的数据用该组区间的中点值作代表)
x的范围 (-2,+2) (-6,+6)
频率 0.682 7 0.954 5
参考答案
一、单项选择题
1.A ①中,在不同分数段内的同学的考试成绩有明显的差异,用分层随机抽样比较恰当;②中,总体包含的个体较少,用简单随机抽样比较恰当.
2.B 设样本容量为n,因为3个校区学生数之比为2∶3∶5,最多的一个校区抽出的个体数是60,所以n×=60,解得n=120.故选B.
3.D 因为10×70%=7,所以70%分位数为,所以解得9≤x≤10.
4.D 由题意知,随机抽查的100人中只能说出一句或一句也说不出的同学有100-45-32=23(人),故只能说出一句或一句也说不出的学生占的比例为,故只能说出一句或一句也说不出的学生大约有500×=115(人).
5.B 对于A,由扇形图可得总人数为1 500+2 000+2 500=6 000,故样本容量为6 000×4%=240,故A说法正确;对于B,当m=50时,满意的人数为2 000×0.3+1 500×0.2+2 500×0.5=2 150,故满意度为=0.4,故B说法错误;对于C,总体中对方式二满意的学生人数约为1 500×0.2=300,故C说法正确;对于D,样本中对方式一满意的学生人数为2 000×4%×
6.B 因为初中学生中课外阅读时间不小于30 h的频率为(0.02+0.005)×10=0.25,所以该校所有的初中学生中,课外阅读时间不小于30 h的学生人数约为0.25×1 800=450.同理,高中学生中课外阅读时间不小于30 h的频率为(0.03+0.005)×10=0.35,故该校所有的高中学生中,课外阅读时间不小于30 h的学生人数约为0.35×1 200=420.所以该校所有学生中,课外阅读时间不小于30 h的学生人数约为450+420=870.
7.B
A 由(0.01+a+0.035+0.03+0.01)×10=1,可得a=0.015.
B √ 前三个矩形的面积和为0.1+0.15+0.35=0.6,所以估计这20名学生数学考试成绩的第60百分位数为80.
C 估计这20名学生数学考试成绩的众数为=75.
D 这20名学生数学考试成绩落在[50,60)内的学生人数为20×0.1=2,则估计总体中成绩落在[50,60)内的学生人数为×2=100.
8.C
A 当投掷骰子出现结果为1,2,3,4,6,6,6时,满足平均数为4,中位数为4,可以出现点数6.
B 当投掷骰子出现结果为3,3,3,4,4,5,6时,满足中位数为4,众数为3,可以出现点数6.
C 若平均数为3,且出现6点,则方差s2>(6-3)2=>1,所以平均数为3,方差为1时,一定没有出现点数6.
D 当投掷骰子出现结果为2,2,3,3,6,6,6时,满足中位数为3,平均数为(2+2+3+3+6+6+6)=4,方差为s2=[(2-4)2+(2-4)2+(3-4)2+(3-4)2+(6-4)2+(6-4)2+(6-4)2]=,可以出现点数6.
由以上分析知选C.
二、多项选择题
9.AB 设丢失的数据为x,则这七个数据的平均数为,众数是3.因为这组数据的平均数与众数的和是中位数的2倍,所以若x≤3,则中位数为3,此时+3=2×3,解得x=-10;若3
A 2016年至2018年,中国雪场滑雪人次的同比增长率逐年增加,2018年至2021年同比增长率逐年下降.
B √ 由条形图可知,2016年至2021年,中国雪场滑雪人次逐年增加.
C 由统计图可知,2016年与2021年,中国雪场滑雪人次的同比增长率近似相等,但是2015年滑雪人次为800万,2020年滑雪人次为1750万,同比增长基数差距大,同比增长人数不相等.
D √ 由统计图可知,2016年至2021年,中国雪场滑雪人次的增长率约为×100%≈118.9%.
11.ABC 根据抽样方法,可知这种抽样方法是简单随机抽样,A正确;易知这5名男生成绩的中位数是90,这5名女生成绩的中位数是93,故B正确;5名男生成绩的平均数为(86+94+88+92+90)÷5=90,方差为[(86-90)2+(94-90)2+(88-90)2+(92-90)2+(90-90)2]=8,5名女生成绩的平均数为(88+93+93+88+93)÷5=91,方差为[(88-91)2+(93-91)2+(93-91)2+(88-91)2+(93-91)2]=6,故C正确;由于该班男生成绩的平均数与该班女生成绩的平均数不一定是样本的平均数,故D错误.
12. ABD
A √ 由题图可得100×(0.001+0.002+0.002 6×2+a+0.000 4)=1,解得a=0.001 4,故样本在区间[500,700]内的频数为100×(0.001 4+0.000 4)×100=18.
B √ 年收入在300万元以内的企业的频率为100×(0.001+0.002)=0.3.
C 100×(0.001+0.002+0.002 6)=0.56>0.5,则中位数在[300,400)内,设为x,则(x-300)×0.002 6=0.5-0.3,得x≈377>350.
D √ 样本年收入的平均数为100×(150×0.001+250×0.002+350×0.002 6+450×0.002 6+550×0.001 4+650×0.000 4)=376(万元),则估计当地的中小型企业年收入的平均数为376万元.
三、填空题
13.7或8或9或10(填上述4个数中任意一个均可) 解析7,6,8,9,8,7,10,m,若去掉m,该组数据从小到大排列为:6,7,7,8,8,9,10,则7×0.25=1.75,故第25百分位数为第二个数即7,所以7,6,8,9,8,7,10,m的第25百分位数为7,而8×0.25=2,所以7为将7,6,8,9,8,7,10,m从小到大排列后的第二个数与第三个数的平均数,所以m(1≤m≤10)的值可以是7或8或9或10.(注:写出一个满足题意的答案即可.)
14.3 解析第3组的人数为100×5×0.06=30,第4组的人数为100×5×0.04=20,第5组的人数为100×5×0.02=10,所以这三组共有60名志愿者,所以利用分层随机抽样的方法在60名志愿者中抽取6名志愿者,第3组应抽取6×=3(名).
15.21 110 解析因为样本数据由小到大依次为2,3,3,7,a,b,12,13,19,20(a,b∈N),且样本的中位数为10.5,所以=10.5,即a+b=21,所以样本的平均数为=10.要使样本方差最小,即(a-10)2+(b-10)2最小,又(a-10)2+(b-10)2=(21-b-10)2+(b-10)2=(11-b)2+(b-10)2=2b2-42b+221=2(b-)2+,且b∈N,所以当b=11或b=10时,(a-10)2+(b-10)2取得最小值.又a+b=21,所以a=11,b=10或a=10,b=11,所以ab=110.
16.3 解析由题意,一个数由4改为1,另一个数由6改为9,其余数不变,可得该组数据的平均数不变,设没有改变的8个数分别为x1,x2,…,x8,原先一组数据的方差为s2=[(x1-)2+(x2-)2+…+(x8-)2+(4-)2+],新数据的方差为[(x1-)2+(x2-)2+…+(x8-)2+(1-)2+(9-)2],所以-s2=[(1-)2+(9-)2-(4-)2-(6-)2]=(1-2 +81-18-16+8-36+12)=3,所以新的一组数据的方差相比原先一组数据的方差的增加值为3.
四、解答题
17.解析方案一 选择方法一.
同一组数据用该组区间的中点值为代表,得到这100天中该产品每天生产件数的频数分布表如下:
件数 6 000 7 000 8 000 9 000
频数 20 30 40 10
(2分)
使用100台A设备和800台B设备每天可进一步加工的件数为30×100+4×800=6 200,则这100天中该产品每天进一步加工件数的频数分布表如下:
进一步加工的件数 6 000 6 200
频数 20 80
(6分)
所以使用A,B设备进一步加工后的日增加的利润的均值为25×-500×100-80×800=40 000(元).(10分)
方案二 选择方法二.
同一组数据用该组区间的中点值为代表,得到这100天中该产品每天生产件数的频数分布表如下:
件数 6 000 7 000 8 000 9 000
频数 20 30 40 10
(2分)
使用200台A设备和450台B设备每天可进一步加工的件数为30×200+4×450=7 800,则这100天中该产品每天进一步加工件数的频数分布表如下:
进一步加工的件数 6 000 7 000 7 800
频数 20 30 50
(6分)
所以使用A,B设备进一步加工后的日增加的利润的均值为
25×-500×200-80×450=44 000(元).(10分)
18.解析(1)全体高一同学平均身高的估计值为160×+165×+170×+175×+180×+185×+190×=174.2(cm).(5分)
(2)由题图可得,高一男同学的总人数为300,女同学的总人数为200,故由体检数据计算出该校高一学生平均身高为172×+164×=168.8(cm).(8分)
存在差异的原因,参考答案(酌情给分,言之有理即可):
①订购校服时,大多数学生会选择高于自身身高的尺码校服,如身高172 cm的同学,一般会订购175 cm尺码的校服,甚至更大尺码;
②部分同学因考虑舒适或继续长高会订购更大尺码;
③体型偏胖的学生一般会订购比自己身高大的尺码;
④订购校服和体检时,都可能出现误差.(12分)
19.解析(1)平均数<中位数.理由:直方图在左边“拖尾”,和中位数相比,平均数总是在“长尾巴”那边.(2分)
(2)依题意,[20,30),[30,40)两个组的频率之和为=0.05,[50,60),[60,70),[70,80),[80,90]四个组的频率之和为0.1+0.2+0.4+0.2=0.9,
则[40,50)对应的频率为1-0.05-0.9=0.05.
故总体中分数在区间[40,50)上的人数大约为400×0.05=20.(7分)
(3)依题意,样本中分数不小于70的频率为0.4+0.2=0.6,则样本中分数不小于70的人数为100×0.6=60,其中男女生人数都为30,即样本中男生人数为60,女生人数为40,故男生和女生人数的比例为60∶40=3∶2.
所以由样本估计总体可得,总体中男生和女生人数的比例大约为3∶2.(12分)
20.解析(1)因为B餐厅满意指数在内的有30人,所以2×b=,解得b=0.15.
又0.15×2+a×2+0.2×2+0.05×2=1,解得a=0.1.(3分)
(2)设A餐厅满意指数的平均数和方差分别为,,B餐厅满意指数的平均数和方差分别为,,则有=3×0.1+5×0.3+7×0.4+9×0.2=6.4,=(3-6.4)2×0.1+(5-6.4)2×0.3+(7-6.4)2×0.4+(9-6.4)2×0.2=3.24,
=3×0.3+5×0.2+7×0.4+9×0.1=5.6,=(3-5.6)2×0.3+(5-5.6)2×0.2+(7-5.6)2×0.4+(9-5.6)2×0.1=4.04.
综上,A餐厅满意指数的平均数和方差分别为6.4,3.24;
B餐厅满意指数的平均数和方差分别5.6,4.04.(8分)
(3)答案一 A餐厅满意指数的平均数为6.4,方差为3.24,B餐厅满意指数的平均数为5.6,方差为4.04,因为6.4>5.6,3.24<4.04,所以推荐A餐厅.(12分)
答案二 A餐厅满意指数在[2,6)的频率为0.4,在[6,10]的频率为0.6,B餐厅满意指数在[2,6)和[6,10]的频率都为0.5,所以推荐A餐厅.
(答案不唯一,言之有理即可.)(12分)
21.解析(1)由题意,(0.01+0.015+0.020+2x+0.030+0.035+0.040)×5=1,解得x=0.025.(2分)
=(22.5×0.010+27.5×0.025+32.5×0.035+37.5×0.040+42.5×0.030+47.5×0.025+52.5×0.020+57.5×0.015)×5≈39.6(岁).(4分)
(2)通过计算知第75百分位数落在[45,50)区间内,设为t,则(0.010+0.025+0.035+0.040+0.030)×5+(t-45)×0.025=0.75,
解得t=47,即第75百分位数为47.(7分)
(3)设该名选手最终的平均分为,最终方差为s2,
则(8.4×8+8.8×10+9.4×12)≈8.933(分),(9分)
s2={8[]+12[+()2]}={8[0.015+(8.4-8.933)2]+10[0.054+(8.8-8.933)2]+12[0.064+(9.4-8.933)2]}≈0.216.
估计该选手最终得分为8.933分,其得分方差为0.216.(12分)
22.解析(1)由频率分布直方图得,一刀宣纸有正牌100×0.1×4=40(张),有副牌100×0.05×4×2=40(张),有废品100×0.025×4×2=20(张),
所以该公司一刀宣纸的利润的估计值为40×15+40×8-20×20=520(元),
所以估计该公司的年利润为520万元.(4分)
(2)由频率分布直方图得,
=42×0.025×4+46×0.05×4+50×0.1×4+54×0.05×4+58×0.025×4=50.(6分)
由表格数据可得一刀宣纸中正牌的张数估计为100×0.682 7=68.27,
废品的张数估计为100×(1-0.954 5)=4.55,
副牌的张数估计为100×(0.954 5-0.682 7)=27.18,
所以一刀宣纸的利润为68.27×12+27.18×5-4.55×20=864.14(元),(9分)
10 000刀宣纸的利润为10 000×864.14=8 641 400(元)=864.14(万元)
所以购买这种机器后该公司的利润为:864.14-100=764.14(万元),
因为764.14>520,所以建议该公司购买这种机器.(12分)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
