10.3 频率与概率同步练习-2022-2023学年高一下学期数学人教A版(2019)必修第二册(含答案)
文档属性
| 名称 | 10.3 频率与概率同步练习-2022-2023学年高一下学期数学人教A版(2019)必修第二册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 139.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 06:59:17 | ||
图片预览



文档简介
《第三节 频率与概率》同步练习
一、基础巩固
知识点1 频率的稳定性
1.(多选)[2022广东惠州一中高二上月考]小明将一枚质地均匀的骰子连续抛掷了30次,每次朝上的点数都是2,则下列说法正确的是( )
A.朝上的点数是2的概率和频率均为1
B.若抛掷30 000次,则朝上的点数是2的频率约为0.17
C.抛掷第31次,朝上的点数一定不是2
D.抛掷6 000次,朝上的点数为2的次数大约为1 000次
2.[2022湖北十堰高中联合体高二上期中]下列说法合理的是( )
A.抛掷一枚质地均匀的骰子,点数为6的概率是,即每掷6次就有一次掷得点数6
B.抛掷一枚硬币,试验200次出现正面的频率不一定比100次得到的频率更接近概率
C.某地气象局预报说,明天本地下雨的概率为80%,是指明天本地有80%的区域下雨
D.随机事件A,B中至少有一个发生的概率一定比A,B中恰有一个发生的概率大
3.在一个不透明的袋中有除颜色外均相同的4个小球,其中有2个白球、1个红球、1个蓝球,每次从袋中摸出1个球,然后放回搅匀再摸,在摸球试验中得到下列表格中部分数据:
摸球次数 10 50 80 100 150 200 250 300
出现红球的频数 2 20 27 36 50
出现红球的频率 30% 26% 24%
(1)请将表中数据补充完整.
(2)如果按照此方法再摸球300次,所得频率与表格中摸球300次对应的频率一定一样吗 为什么
(3)试估计红球出现的概率.
知识点2 随机模拟
4.[2022福建宁德高一下期末]在一个实验中,某种豚鼠被感染A病毒的概率均为40%,现采用随机模拟的方法估计三只豚鼠被感染的概率:先由计算机生成[0,9]之间整数值的随机数,指定1,2,3,4表示被感染,5,6,7,8,9,0表示没有被感染.经随机模拟产生了如下20组随机数:
192907966925271932812458569683
257393127556488730113537989431
据此估计三只豚鼠中至少有一只被感染的概率为( )
A.0.25 B.0.4 C.0.6 D.0.75
5.袋子中有四个小球,分别写有“中”“华”“民”“族”四个字,有放回地从中任取一个小球,直到“中”“华”两个字都取到才停止.用随机模拟的方法估计恰好抽取三次停止的概率,利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“中”“华”“民”“族”这四个字,以三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此估计恰好抽取三次就停止的概率为 .
二、能力提升
1.[2022广东深圳龙城高级中学高一下期中]随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4 500名网上购物消费者进行了调查(每名消费者限选一种情况回答),统计结果如下表:
满意情况 不满意 比较满意 满意 非常满意
人数 200 n 2 100 1 000
根据表中数据,估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率是( )
A. B. C. D.
2.(多选)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物、其他垃圾和有害垃圾四类,并设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市四类垃圾箱中总计1 000 t生活垃圾.经分拣以后数据统计如下表(单位:t),视频率为概率,根据样本估计本市生活垃圾投放情况,下列说法正确的是( )
厨余垃圾箱 可回收物箱 其他垃圾箱 有害垃圾箱
厨余垃圾 400 100 90 10
可回收物 30 220 30 10
其他垃圾 10 20 50 5
有害垃圾 5 10 5 5
A.厨余垃圾投放正确的概率为
B.居民生活垃圾投放错误的概率为
C.该市四类垃圾中投放正确的概率最高的是可回收物
D.厨余垃圾在厨余垃圾箱、可回收物箱、其他垃圾箱、有害垃圾箱中的投放量的平均数为152
3.[2022陕西西安七十五中高一下月考]在一个不透明的布袋中,装有红色、黑色、白色的玻璃球(除颜色外其他完全相同),共有40个.小明通过多次摸球试验后,发现摸到红色、黑色的玻璃球的频率分别稳定在0.15和0.45,则口袋中白色的玻璃球的个数可能是 .
4.受轿车在保修期内的维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,甲品牌车保修期为3年,乙品牌车保修期为2年.现从该厂已售出的两种品牌轿车中分别随机抽取50辆,统计出轿车首次出现故障的时间数据如下:
品牌 甲 乙
首次出现故障的时间x/年 (0,1] (1,2] (2,3] (3,+∞) (0,1] (1,2] (2,+∞)
轿车数量/辆 2 1 3 44 2 3 45
从该厂生产的甲、乙两种品牌轿车中各随机抽取一辆.
(1)估计甲品牌轿车首次出现故障发生在保修期内的概率(将频率视为概率).
(2)求保修期内恰有一辆轿车发生故障的概率.
5.[2022云南丽江高一下期末]随着金融市场的发展,越来越多的人选择投资“黄金”作为理财的手段,下面将A市把黄金作为理财产品的投资人的年龄情况进行统计,得到如图所示的频率分布直方图.
(1)求a的取值,以及把黄金作为理财产品的投资者的年龄的中位数;(中位数结果用小数表示,小数点后保留两位小数)
(2)现按照分层随机抽样的方法从年龄在[40,50)和[60,70]的投资者中随机抽取5人,再从这5人中随机抽取2人进行投资调查,求至少有1人年龄在[60,70]的概率.
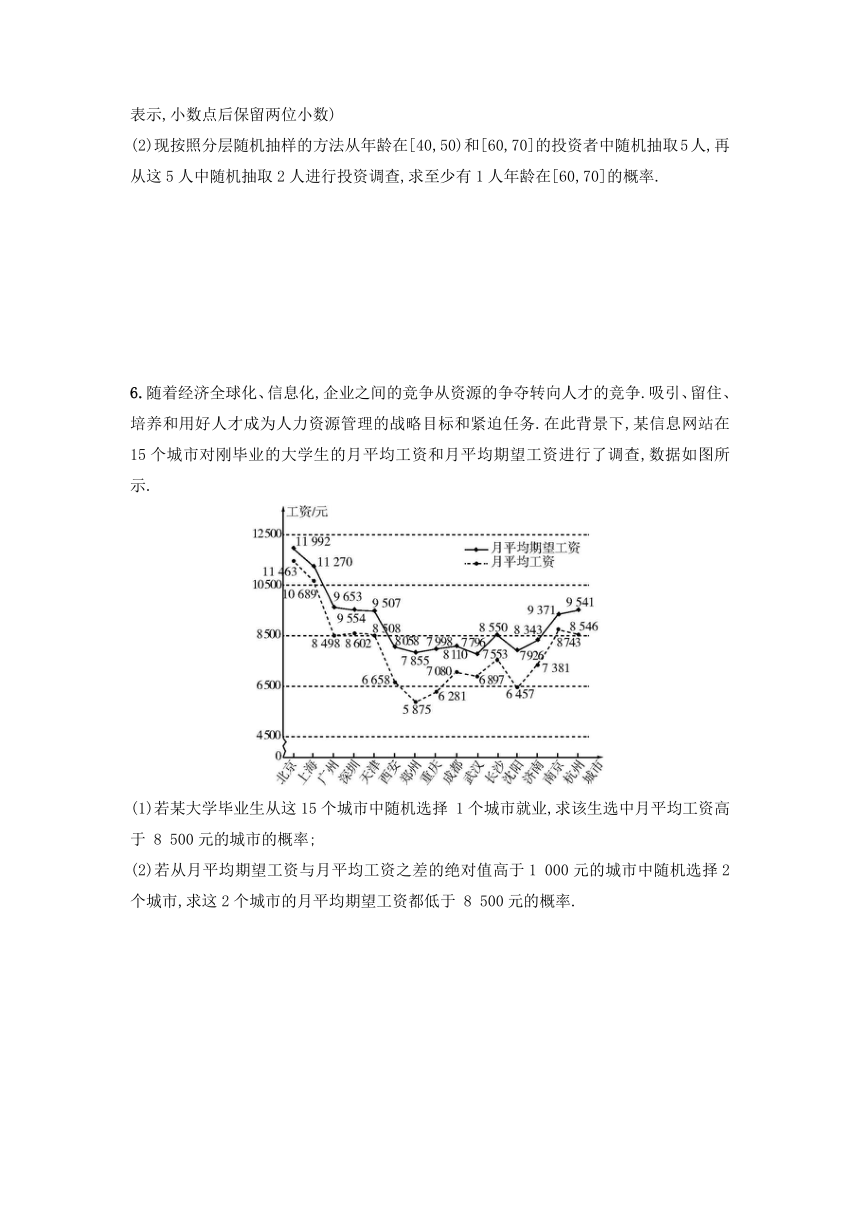
6.随着经济全球化、信息化,企业之间的竞争从资源的争夺转向人才的竞争.吸引、留住、培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市对刚毕业的大学生的月平均工资和月平均期望工资进行了调查,数据如图所示.
(1)若某大学毕业生从这15个城市中随机选择 1个城市就业,求该生选中月平均工资高于 8 500元的城市的概率;
(2)若从月平均期望工资与月平均工资之差的绝对值高于1 000元的城市中随机选择2个城市,求这2个城市的月平均期望工资都低于 8 500元的概率.
7.[2022华中师范大学第一附属中学高一下期末]在中国共产党第二十次全国代表大会开幕会上,习近平同志在报告中用一组组数据,说明十年来我国经济社会发展所取得的非凡成就.某地为了解居民可支配收入情况,随机抽取100人,经统计,这100人去年可支配收入(单位:万元)均在区间[4.5,10.5]内,按[4.5,5.5),[5.5,6.5),[6.5,7.5),[7.5,8.5),
[8.5,9.5),[9.5,10.5]分成6组,频率分布直方图如图所示,若上述居民可支配收入数据的第60百分位数为8.1.
(1)求a,b的值,并估计这100位居民去年可支配收入的平均值(同一组中的数据用该组区间的中点值作代表);
(2)用样本的频率估计概率,从该地居民中抽取甲、乙、丙3人,若每次抽取的结果互不影响,求抽取的3人中至少有2人去年可支配收入在[7.5,8.5)内的概率.
参考答案
一、基础巩固
1.BD 由题意知朝上的点数是2的频率为=1,概率为,故A错误;当抛掷次数很多时,朝上的点数是2的频率在≈0.17附近摆动,故B正确;抛掷第31次,朝上的点数可能是2,也可能不是2,故C错误;每次抛掷朝上的点数是2的概率为,所以抛掷6 000次,朝上的点数为2的次数大约为6 000×=1 000,D正确.
2.B
3.解析(1)
摸球次数 10 50 80 100 150 200 250 300
出现红球的频数 2 15 20 27 36 50 65 72
出现红球的频率 20% 30% 25% 27% 24% 25% 26% 24%
(2)可能不一样,因为频率会随每次试验的变化而变化.
(3)红球出现的频率集中在25%附近,所以可估计红球出现的概率为0.25.
4.D 由题意知,事件A=“三只豚鼠中至少有一只被感染”,则=“三只豚鼠都没被感染”,随机数中满足三只豚鼠都没被感染的有907,966,569,556,989,共5个,故P()==0.25,则P(A)=1-P()=1-0.25=0.75.
5. 解析设事件A=“恰好抽取三次就停止”.由随机模拟产生的随机数,可知恰好抽取三次就停止的有021,001,130,031,共4组随机数,故P(A)=.
二、能力提升
1.C 由题意得,n=4 500-200-2 100-1 000=1 200,因为随机调查的消费者中对网上购物“比较满意”或“满意”的总人数为1 200+2 100=3 300,所以随机调查的消费者中对网上购物“比较满意”或“满意”的频率为.由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率为.
2.ABC 由表格可得厨余垃圾投放正确的概率=,故A正确;居民生活垃圾投放错误的有1 000-(400+220+50+5)=325(t),故生活垃圾投放错误的概率为,故B正确;可回收物投放正确的概率为,其他垃圾投放正确的概率为,有害垃圾投放正确的概率为,所以该市四类垃圾中投放正确的概率最高的是可回收物,故C正确;厨余垃圾在厨余垃圾箱、可回收物箱、其他垃圾箱、有害垃圾箱中的投放量的平均数 =150,故D错误.故选ABC.
3.16 解析根据频率与概率的关系,知摸到红色、黑色的玻璃球的概率分别为0.15,0.45,所以口袋中红色的玻璃球的个数为40×0.15=6,黑色的玻璃球的个数为40×0.45=18,故白色的玻璃球的个数为40-6-18=16.
4.解析(1)设事件A,B,C分别表示事件甲品牌轿车首次出现故障发生在第1年,第2年和第3年之内,设事件D表示甲品牌轿车首次出现故障发生在保修期内.
因为A,B,C是互斥事件,其概率分别为P(A)=,P(B)=,P(C)=,
所以P(D)=P(A+B+C)=P(A)+P(B)+P(C)=,
所以估计甲品牌轿车首次出现故障发生在保修期内的概率为.
(2)同(1)可得乙品牌轿车首次出现故障发生在保修期内的概率为.
设事件E表示保修期内恰有一辆轿车发生故障,则P(E)=.
5.解析(1)依题意,0.07+0.18+10a+0.25+0.2=1,解得a=0.030,
因为前2组的频率和为10×(0.007+0.018)=0.25<0.5,前3组的频率和为10×(0.007+0.018+0.030)=0.55>0.5,
所以所求中位数为40+≈48.33.
(2)由频率分布直方图可知年龄在[40,50)和[60,70]的频率分别为0.3,0.2,
所以应从年龄在[40,50)的投资者中抽取3人,记为A,B,C,
从年龄在[60,70]的投资者中抽取2人,记为a,b,则从这5人中任取2人的所有情况为(A,B),(A,C),(B,C),(a,b),(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),共10种,
满足条件的为(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),(a,b),共7种,
故至少有1人年龄在[60,70]的概率为P=.
6.解析(1)设“该生选中月平均工资高于8 500元的城市”为事件E,
15个城市中月平均工资高于8 500元的有6个,
所以 P(E)=.
(2)月平均期望工资与月平均工资之差的绝对值高于1 000元的城市有6个,
其中月平均期望工资高于8 500元的有1个,记为A;月平均期望工资低于8 500元的有5个,记为B1,B2,B3,B4,B5.
选取2个城市的样本空间为{AB1,AB2,AB3,AB4,AB5,B1B2,B1B3,B1B4,B1B5,B2B3,B2B4,B2B5,B3B4,
B3B5,B4B5},共15个样本点,其中2个城市的月平均期望工资都低于8 500元的样本空间为{B1B2,B1B3,B1B4,B1B5,B2B3,B2B4,B2B5,B3B4,B3B5,B4B5},共10个样本点.
所以所求概率为.
7.解析(1)由频率分布直方图可得,0.05+0.12+a+b+0.2+0.08=1,则a+b=0.55. ①
因为居民可支配收入数据的第60百分位数为8.1,
所以0.05+0.12+a+(8.1-7.5)·b=0.6,
则a+0.6b=0.43. ②
将①与②联立,解得
所以这100位居民去年可支配收入的平均值为0.05×5+0.12×6+0.25×7+0.3×8+0.2×9+0.08×10=7.72(万元).
(2)根据题意,设事件A,B,C分别为甲、乙、丙在[7.5,8.5)内,则P(A)=P(B)=P(C)=0.3.
①设事件M=“抽取的3人中有2人在[7.5,8.5)内”,则M=AB+AC+BC,且AB与AC与BC互斥,根据概率的加法公式和事件独立性定义,得
P(M)=P(AB+AC+BC)=0.3×0.3×(1-0.3)+0.3×(1-0.3)×0.3+(1-0.3)×0.3×0.3=0.189.
②设事件N=“抽取的3人都在[7.5,8.5)内”,则N=ABC,由事件的独立性定义,得
P(N)=P(ABC)=P(A)P(B)P(C)=0.3×0.3×0.3=0.027.
设事件D=“抽取的3人中至少有2人去年可支配收入在[7.5,8.5)内”,则P(D)=P(M)+P(N)=0.189+0.027=0.216.
一、基础巩固
知识点1 频率的稳定性
1.(多选)[2022广东惠州一中高二上月考]小明将一枚质地均匀的骰子连续抛掷了30次,每次朝上的点数都是2,则下列说法正确的是( )
A.朝上的点数是2的概率和频率均为1
B.若抛掷30 000次,则朝上的点数是2的频率约为0.17
C.抛掷第31次,朝上的点数一定不是2
D.抛掷6 000次,朝上的点数为2的次数大约为1 000次
2.[2022湖北十堰高中联合体高二上期中]下列说法合理的是( )
A.抛掷一枚质地均匀的骰子,点数为6的概率是,即每掷6次就有一次掷得点数6
B.抛掷一枚硬币,试验200次出现正面的频率不一定比100次得到的频率更接近概率
C.某地气象局预报说,明天本地下雨的概率为80%,是指明天本地有80%的区域下雨
D.随机事件A,B中至少有一个发生的概率一定比A,B中恰有一个发生的概率大
3.在一个不透明的袋中有除颜色外均相同的4个小球,其中有2个白球、1个红球、1个蓝球,每次从袋中摸出1个球,然后放回搅匀再摸,在摸球试验中得到下列表格中部分数据:
摸球次数 10 50 80 100 150 200 250 300
出现红球的频数 2 20 27 36 50
出现红球的频率 30% 26% 24%
(1)请将表中数据补充完整.
(2)如果按照此方法再摸球300次,所得频率与表格中摸球300次对应的频率一定一样吗 为什么
(3)试估计红球出现的概率.
知识点2 随机模拟
4.[2022福建宁德高一下期末]在一个实验中,某种豚鼠被感染A病毒的概率均为40%,现采用随机模拟的方法估计三只豚鼠被感染的概率:先由计算机生成[0,9]之间整数值的随机数,指定1,2,3,4表示被感染,5,6,7,8,9,0表示没有被感染.经随机模拟产生了如下20组随机数:
192907966925271932812458569683
257393127556488730113537989431
据此估计三只豚鼠中至少有一只被感染的概率为( )
A.0.25 B.0.4 C.0.6 D.0.75
5.袋子中有四个小球,分别写有“中”“华”“民”“族”四个字,有放回地从中任取一个小球,直到“中”“华”两个字都取到才停止.用随机模拟的方法估计恰好抽取三次停止的概率,利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“中”“华”“民”“族”这四个字,以三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此估计恰好抽取三次就停止的概率为 .
二、能力提升
1.[2022广东深圳龙城高级中学高一下期中]随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4 500名网上购物消费者进行了调查(每名消费者限选一种情况回答),统计结果如下表:
满意情况 不满意 比较满意 满意 非常满意
人数 200 n 2 100 1 000
根据表中数据,估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率是( )
A. B. C. D.
2.(多选)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物、其他垃圾和有害垃圾四类,并设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市四类垃圾箱中总计1 000 t生活垃圾.经分拣以后数据统计如下表(单位:t),视频率为概率,根据样本估计本市生活垃圾投放情况,下列说法正确的是( )
厨余垃圾箱 可回收物箱 其他垃圾箱 有害垃圾箱
厨余垃圾 400 100 90 10
可回收物 30 220 30 10
其他垃圾 10 20 50 5
有害垃圾 5 10 5 5
A.厨余垃圾投放正确的概率为
B.居民生活垃圾投放错误的概率为
C.该市四类垃圾中投放正确的概率最高的是可回收物
D.厨余垃圾在厨余垃圾箱、可回收物箱、其他垃圾箱、有害垃圾箱中的投放量的平均数为152
3.[2022陕西西安七十五中高一下月考]在一个不透明的布袋中,装有红色、黑色、白色的玻璃球(除颜色外其他完全相同),共有40个.小明通过多次摸球试验后,发现摸到红色、黑色的玻璃球的频率分别稳定在0.15和0.45,则口袋中白色的玻璃球的个数可能是 .
4.受轿车在保修期内的维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,甲品牌车保修期为3年,乙品牌车保修期为2年.现从该厂已售出的两种品牌轿车中分别随机抽取50辆,统计出轿车首次出现故障的时间数据如下:
品牌 甲 乙
首次出现故障的时间x/年 (0,1] (1,2] (2,3] (3,+∞) (0,1] (1,2] (2,+∞)
轿车数量/辆 2 1 3 44 2 3 45
从该厂生产的甲、乙两种品牌轿车中各随机抽取一辆.
(1)估计甲品牌轿车首次出现故障发生在保修期内的概率(将频率视为概率).
(2)求保修期内恰有一辆轿车发生故障的概率.
5.[2022云南丽江高一下期末]随着金融市场的发展,越来越多的人选择投资“黄金”作为理财的手段,下面将A市把黄金作为理财产品的投资人的年龄情况进行统计,得到如图所示的频率分布直方图.
(1)求a的取值,以及把黄金作为理财产品的投资者的年龄的中位数;(中位数结果用小数表示,小数点后保留两位小数)
(2)现按照分层随机抽样的方法从年龄在[40,50)和[60,70]的投资者中随机抽取5人,再从这5人中随机抽取2人进行投资调查,求至少有1人年龄在[60,70]的概率.
6.随着经济全球化、信息化,企业之间的竞争从资源的争夺转向人才的竞争.吸引、留住、培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市对刚毕业的大学生的月平均工资和月平均期望工资进行了调查,数据如图所示.
(1)若某大学毕业生从这15个城市中随机选择 1个城市就业,求该生选中月平均工资高于 8 500元的城市的概率;
(2)若从月平均期望工资与月平均工资之差的绝对值高于1 000元的城市中随机选择2个城市,求这2个城市的月平均期望工资都低于 8 500元的概率.
7.[2022华中师范大学第一附属中学高一下期末]在中国共产党第二十次全国代表大会开幕会上,习近平同志在报告中用一组组数据,说明十年来我国经济社会发展所取得的非凡成就.某地为了解居民可支配收入情况,随机抽取100人,经统计,这100人去年可支配收入(单位:万元)均在区间[4.5,10.5]内,按[4.5,5.5),[5.5,6.5),[6.5,7.5),[7.5,8.5),
[8.5,9.5),[9.5,10.5]分成6组,频率分布直方图如图所示,若上述居民可支配收入数据的第60百分位数为8.1.
(1)求a,b的值,并估计这100位居民去年可支配收入的平均值(同一组中的数据用该组区间的中点值作代表);
(2)用样本的频率估计概率,从该地居民中抽取甲、乙、丙3人,若每次抽取的结果互不影响,求抽取的3人中至少有2人去年可支配收入在[7.5,8.5)内的概率.
参考答案
一、基础巩固
1.BD 由题意知朝上的点数是2的频率为=1,概率为,故A错误;当抛掷次数很多时,朝上的点数是2的频率在≈0.17附近摆动,故B正确;抛掷第31次,朝上的点数可能是2,也可能不是2,故C错误;每次抛掷朝上的点数是2的概率为,所以抛掷6 000次,朝上的点数为2的次数大约为6 000×=1 000,D正确.
2.B
3.解析(1)
摸球次数 10 50 80 100 150 200 250 300
出现红球的频数 2 15 20 27 36 50 65 72
出现红球的频率 20% 30% 25% 27% 24% 25% 26% 24%
(2)可能不一样,因为频率会随每次试验的变化而变化.
(3)红球出现的频率集中在25%附近,所以可估计红球出现的概率为0.25.
4.D 由题意知,事件A=“三只豚鼠中至少有一只被感染”,则=“三只豚鼠都没被感染”,随机数中满足三只豚鼠都没被感染的有907,966,569,556,989,共5个,故P()==0.25,则P(A)=1-P()=1-0.25=0.75.
5. 解析设事件A=“恰好抽取三次就停止”.由随机模拟产生的随机数,可知恰好抽取三次就停止的有021,001,130,031,共4组随机数,故P(A)=.
二、能力提升
1.C 由题意得,n=4 500-200-2 100-1 000=1 200,因为随机调查的消费者中对网上购物“比较满意”或“满意”的总人数为1 200+2 100=3 300,所以随机调查的消费者中对网上购物“比较满意”或“满意”的频率为.由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率为.
2.ABC 由表格可得厨余垃圾投放正确的概率=,故A正确;居民生活垃圾投放错误的有1 000-(400+220+50+5)=325(t),故生活垃圾投放错误的概率为,故B正确;可回收物投放正确的概率为,其他垃圾投放正确的概率为,有害垃圾投放正确的概率为,所以该市四类垃圾中投放正确的概率最高的是可回收物,故C正确;厨余垃圾在厨余垃圾箱、可回收物箱、其他垃圾箱、有害垃圾箱中的投放量的平均数 =150,故D错误.故选ABC.
3.16 解析根据频率与概率的关系,知摸到红色、黑色的玻璃球的概率分别为0.15,0.45,所以口袋中红色的玻璃球的个数为40×0.15=6,黑色的玻璃球的个数为40×0.45=18,故白色的玻璃球的个数为40-6-18=16.
4.解析(1)设事件A,B,C分别表示事件甲品牌轿车首次出现故障发生在第1年,第2年和第3年之内,设事件D表示甲品牌轿车首次出现故障发生在保修期内.
因为A,B,C是互斥事件,其概率分别为P(A)=,P(B)=,P(C)=,
所以P(D)=P(A+B+C)=P(A)+P(B)+P(C)=,
所以估计甲品牌轿车首次出现故障发生在保修期内的概率为.
(2)同(1)可得乙品牌轿车首次出现故障发生在保修期内的概率为.
设事件E表示保修期内恰有一辆轿车发生故障,则P(E)=.
5.解析(1)依题意,0.07+0.18+10a+0.25+0.2=1,解得a=0.030,
因为前2组的频率和为10×(0.007+0.018)=0.25<0.5,前3组的频率和为10×(0.007+0.018+0.030)=0.55>0.5,
所以所求中位数为40+≈48.33.
(2)由频率分布直方图可知年龄在[40,50)和[60,70]的频率分别为0.3,0.2,
所以应从年龄在[40,50)的投资者中抽取3人,记为A,B,C,
从年龄在[60,70]的投资者中抽取2人,记为a,b,则从这5人中任取2人的所有情况为(A,B),(A,C),(B,C),(a,b),(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),共10种,
满足条件的为(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),(a,b),共7种,
故至少有1人年龄在[60,70]的概率为P=.
6.解析(1)设“该生选中月平均工资高于8 500元的城市”为事件E,
15个城市中月平均工资高于8 500元的有6个,
所以 P(E)=.
(2)月平均期望工资与月平均工资之差的绝对值高于1 000元的城市有6个,
其中月平均期望工资高于8 500元的有1个,记为A;月平均期望工资低于8 500元的有5个,记为B1,B2,B3,B4,B5.
选取2个城市的样本空间为{AB1,AB2,AB3,AB4,AB5,B1B2,B1B3,B1B4,B1B5,B2B3,B2B4,B2B5,B3B4,
B3B5,B4B5},共15个样本点,其中2个城市的月平均期望工资都低于8 500元的样本空间为{B1B2,B1B3,B1B4,B1B5,B2B3,B2B4,B2B5,B3B4,B3B5,B4B5},共10个样本点.
所以所求概率为.
7.解析(1)由频率分布直方图可得,0.05+0.12+a+b+0.2+0.08=1,则a+b=0.55. ①
因为居民可支配收入数据的第60百分位数为8.1,
所以0.05+0.12+a+(8.1-7.5)·b=0.6,
则a+0.6b=0.43. ②
将①与②联立,解得
所以这100位居民去年可支配收入的平均值为0.05×5+0.12×6+0.25×7+0.3×8+0.2×9+0.08×10=7.72(万元).
(2)根据题意,设事件A,B,C分别为甲、乙、丙在[7.5,8.5)内,则P(A)=P(B)=P(C)=0.3.
①设事件M=“抽取的3人中有2人在[7.5,8.5)内”,则M=AB+AC+BC,且AB与AC与BC互斥,根据概率的加法公式和事件独立性定义,得
P(M)=P(AB+AC+BC)=0.3×0.3×(1-0.3)+0.3×(1-0.3)×0.3+(1-0.3)×0.3×0.3=0.189.
②设事件N=“抽取的3人都在[7.5,8.5)内”,则N=ABC,由事件的独立性定义,得
P(N)=P(ABC)=P(A)P(B)P(C)=0.3×0.3×0.3=0.027.
设事件D=“抽取的3人中至少有2人去年可支配收入在[7.5,8.5)内”,则P(D)=P(M)+P(N)=0.189+0.027=0.216.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
