生活中的轴对称[下学期]
图片预览



文档简介
课件17张PPT。生活中的轴对称回顾与思考1、轴对称与轴对称图形是否是同一回事?
它们有何区别与联系?答:“轴对称”是指两个图形之间的形状与位置关系;“轴对称图形”是指一个图形的位置与形状关系。 一个图形可分割成两个图形,当这两个图形关于某直线对称时原来的那个图形就是轴对称图形;
反过来,如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形。 2、一个轴对称图形的对称轴是否只有一条?答:不一定只有一条。
有的轴对称图形的对称轴不一定只有一条。
通常画出所有的对称轴,这样有利于多角度、
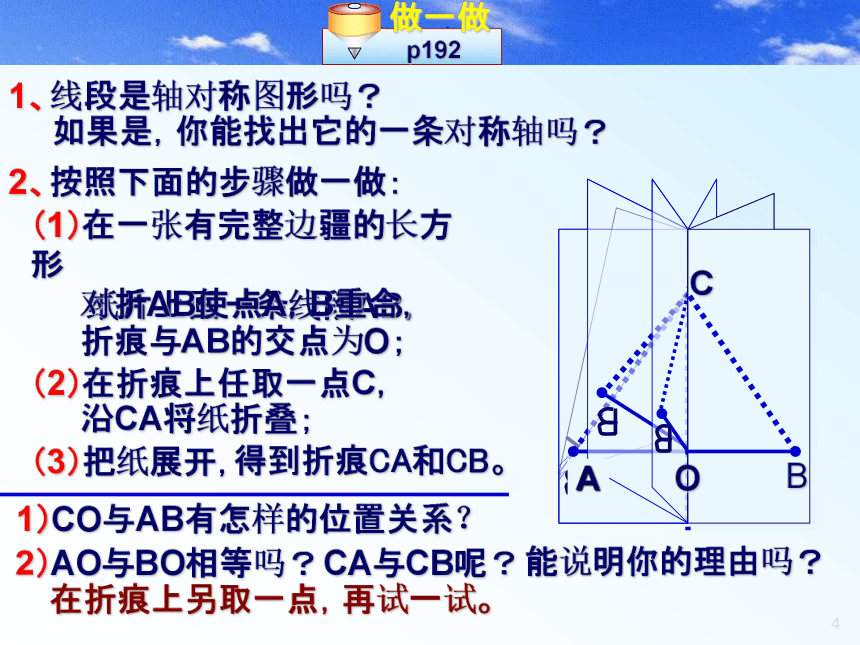
灵活地研究几何图形。 学 习 目 标做一做1、线段是轴对称图形吗?如果是,你能找出它的一条对称轴吗?2、按照下面的步骤做一做:(1)在一张有完整边疆的长方形
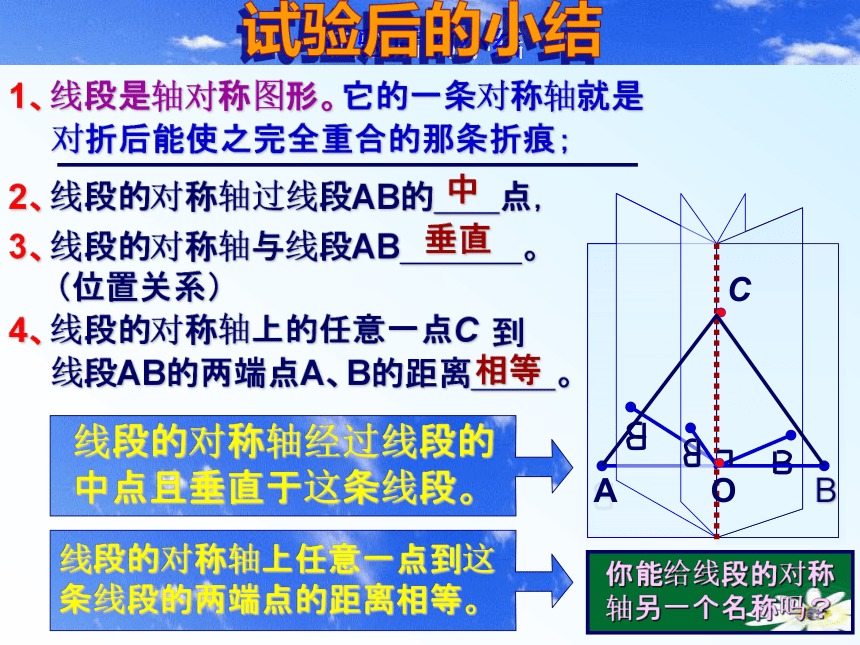
纸片上画一条线段AB,对折AB使点A,B重合,折痕与AB的交点为O;O(2)在折痕上任取一点C,沿CA将纸折叠;(3)把纸展开,AO得到折痕CA和CB。2)AO与BO相等吗?CA与CB呢?能说明你的理由吗?在折痕上另取一点,再试一试。试验后的小结1、线段是轴对称图形。试验后的小结对折后能使之完全重合的那条折痕;2、线段的对称轴过线段AB的 点,中O3、线段的对称轴与线段AB 。
(位置关系)垂直4、线段的对称轴上的任意一点C 到
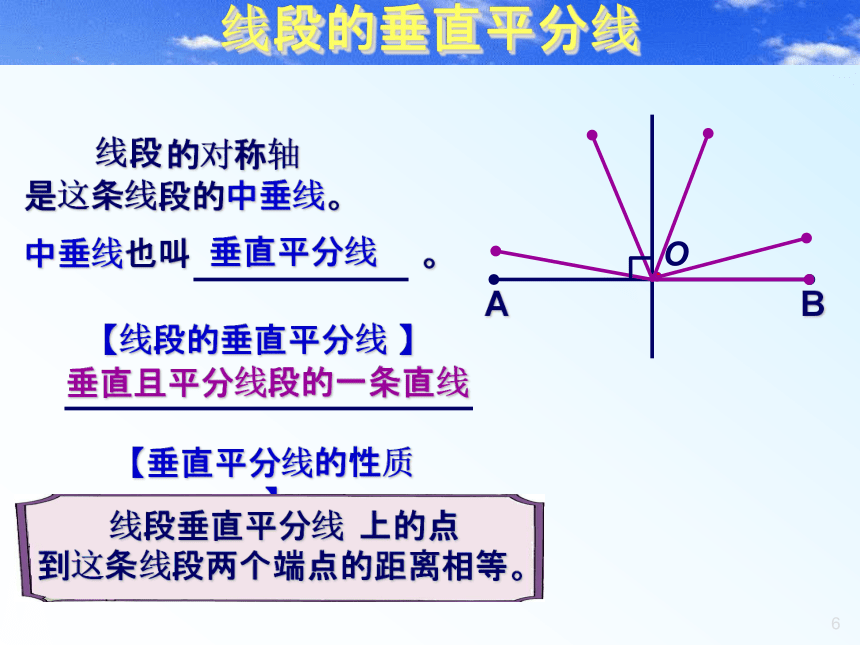
线段AB的两端点A、B的距离 。相等你能给线段的对称轴另一个名称吗?线段的对称轴是这条线段的中垂线。垂直平分线垂直且平分线段的一条直线线段的垂直平分线 上的点
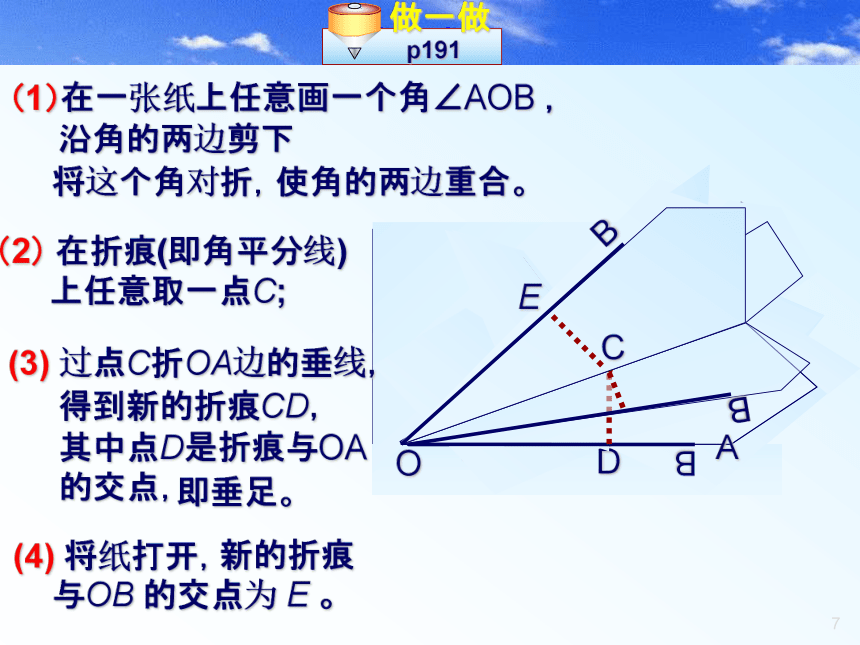
到这条线段两个端点的距离相等。做一做(1)在一张纸上任意画一个角∠AOB ,AOB沿角的两边剪下将这个角对折,使角的两边重合。(2) 在折痕(即角平分线)
上任意取一点C;(3) 过点C折OA边的垂线,得到新的折痕CD,其中点D是折痕与OA
的交点,即垂足。(4) 将纸打开, 新的折痕
与OB 的交点为 E 。EAOB(1)角是轴对称图形吗?如果是,请找出它的
对称轴;角的对称轴是 角的平分线所在的直线。角平分线的性质(2)在上述的操作过程中,
你发现了哪些线段相等?
说说你的理由。CE=CD 角的平分线上的点到这个角的两边的距离相等。E在折痕上另取一点,
再试一试。随堂练习 1、如图,在Rt△ABC 中, 角平分线与垂直平分线的性质,
为我们证明两线段相等 又提供了新的方法与途径。ABCBD是∠B 的平分线 ,DE⊥AB,垂足为E,EDE与DC 相等吗?答:DE=BC。∵ DC⊥BC,垂足为E,∵ DE⊥BA,垂足为E,BD是∠ABC的平分线(D在∠ABC的平分线上) ∴ DE=BC。为什么?接拓展练习感悟与反思小结角的平分线的性质—— 本节课你学到了什么?线段的对称轴是线段的垂直平分线;角的对称轴是角的平分线所在的直线; 线段垂直平分线上的点
到这条线段两个端点的距离相等。 角的平分线上的点到这个角的两边的距离相等。P193页—— 1、 2、3。作 业7.2 拓展练习 尺规作线段的中垂线拓展练习观察领悟作法,探索思考证明方法:AB拓展练习 尺规作角的平分线拓展练习观察领悟作法,探索思考证明方法:ABC拓展练习拓展练习 如图,在△ABC中,∠C等于900,AB的中垂线DE交BC于D,交AB于E,连接AD,若AD平分∠BAC,找出图中相等的线段,并说说你的理由。CBE你能找到图中特殊的三角形吗?你能找到图中相等的角吗?解:∵ AB的中垂线DE交BC于D,
交AB于E,∴ EB=EA ,DB=DA ;∵ AD平分∠BAC ,DC⊥AC、DE⊥AB,∴ DC=DE 。Rt△AcD、Rt△AED、Rt△ACB、Rt△BED、等腰△DBA。EDBCA解:∵DE是线段BC的垂直平分线 ,∴EC=EB∴△BCE 的周长
=EB+EC+BC
=6+6+10=22。 △ABC中,BC=10,边BC 的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE 的周长.拓展练习拓展练习6=6BE=6 某一个星期六,某中学初一年级的同学参加义务劳动,
其中有四个班的同学分别在M、N两处参加劳动,另外四个班的同学分别在道路AB、AC两处劳动,现要在道路AB、AC的交叉区域内设一个荼水供应点P ,使P到两条道路的距离相等,且使 PM= PN,请你找出点P的位置,并说明理由。 AMBNC拓展练习拓展练习P谢谢同学们的合作再见
它们有何区别与联系?答:“轴对称”是指两个图形之间的形状与位置关系;“轴对称图形”是指一个图形的位置与形状关系。 一个图形可分割成两个图形,当这两个图形关于某直线对称时原来的那个图形就是轴对称图形;
反过来,如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形。 2、一个轴对称图形的对称轴是否只有一条?答:不一定只有一条。
有的轴对称图形的对称轴不一定只有一条。
通常画出所有的对称轴,这样有利于多角度、
灵活地研究几何图形。 学 习 目 标做一做1、线段是轴对称图形吗?如果是,你能找出它的一条对称轴吗?2、按照下面的步骤做一做:(1)在一张有完整边疆的长方形
纸片上画一条线段AB,对折AB使点A,B重合,折痕与AB的交点为O;O(2)在折痕上任取一点C,沿CA将纸折叠;(3)把纸展开,AO得到折痕CA和CB。2)AO与BO相等吗?CA与CB呢?能说明你的理由吗?在折痕上另取一点,再试一试。试验后的小结1、线段是轴对称图形。试验后的小结对折后能使之完全重合的那条折痕;2、线段的对称轴过线段AB的 点,中O3、线段的对称轴与线段AB 。
(位置关系)垂直4、线段的对称轴上的任意一点C 到
线段AB的两端点A、B的距离 。相等你能给线段的对称轴另一个名称吗?线段的对称轴是这条线段的中垂线。垂直平分线垂直且平分线段的一条直线线段的垂直平分线 上的点
到这条线段两个端点的距离相等。做一做(1)在一张纸上任意画一个角∠AOB ,AOB沿角的两边剪下将这个角对折,使角的两边重合。(2) 在折痕(即角平分线)
上任意取一点C;(3) 过点C折OA边的垂线,得到新的折痕CD,其中点D是折痕与OA
的交点,即垂足。(4) 将纸打开, 新的折痕
与OB 的交点为 E 。EAOB(1)角是轴对称图形吗?如果是,请找出它的
对称轴;角的对称轴是 角的平分线所在的直线。角平分线的性质(2)在上述的操作过程中,
你发现了哪些线段相等?
说说你的理由。CE=CD 角的平分线上的点到这个角的两边的距离相等。E在折痕上另取一点,
再试一试。随堂练习 1、如图,在Rt△ABC 中, 角平分线与垂直平分线的性质,
为我们证明两线段相等 又提供了新的方法与途径。ABCBD是∠B 的平分线 ,DE⊥AB,垂足为E,EDE与DC 相等吗?答:DE=BC。∵ DC⊥BC,垂足为E,∵ DE⊥BA,垂足为E,BD是∠ABC的平分线(D在∠ABC的平分线上) ∴ DE=BC。为什么?接拓展练习感悟与反思小结角的平分线的性质—— 本节课你学到了什么?线段的对称轴是线段的垂直平分线;角的对称轴是角的平分线所在的直线; 线段垂直平分线上的点
到这条线段两个端点的距离相等。 角的平分线上的点到这个角的两边的距离相等。P193页—— 1、 2、3。作 业7.2 拓展练习 尺规作线段的中垂线拓展练习观察领悟作法,探索思考证明方法:AB拓展练习 尺规作角的平分线拓展练习观察领悟作法,探索思考证明方法:ABC拓展练习拓展练习 如图,在△ABC中,∠C等于900,AB的中垂线DE交BC于D,交AB于E,连接AD,若AD平分∠BAC,找出图中相等的线段,并说说你的理由。CBE你能找到图中特殊的三角形吗?你能找到图中相等的角吗?解:∵ AB的中垂线DE交BC于D,
交AB于E,∴ EB=EA ,DB=DA ;∵ AD平分∠BAC ,DC⊥AC、DE⊥AB,∴ DC=DE 。Rt△AcD、Rt△AED、Rt△ACB、Rt△BED、等腰△DBA。EDBCA解:∵DE是线段BC的垂直平分线 ,∴EC=EB∴△BCE 的周长
=EB+EC+BC
=6+6+10=22。 △ABC中,BC=10,边BC 的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE 的周长.拓展练习拓展练习6=6BE=6 某一个星期六,某中学初一年级的同学参加义务劳动,
其中有四个班的同学分别在M、N两处参加劳动,另外四个班的同学分别在道路AB、AC两处劳动,现要在道路AB、AC的交叉区域内设一个荼水供应点P ,使P到两条道路的距离相等,且使 PM= PN,请你找出点P的位置,并说明理由。 AMBNC拓展练习拓展练习P谢谢同学们的合作再见
