人教版八年级数学下册 18.2.2 菱形 同步练习(含解析)
文档属性
| 名称 | 人教版八年级数学下册 18.2.2 菱形 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 819.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-19 17:07:10 | ||
图片预览



文档简介
18.2.2 菱形 同步练习
一、单选题
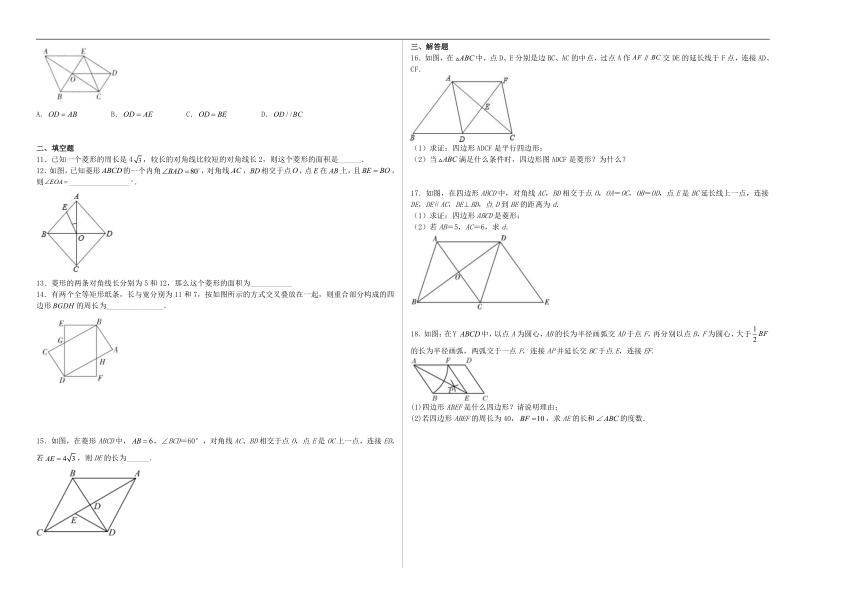
1.如图,在菱形中,过顶点作交对角线于点,已知,则的大小为( ).
A.20° B.25° C.65° D.75°
2.矩形具有而菱形不具有的性质是( )
A.对角线相等 B.对角线平分一组对角
C.对角线互相平分 D.对角线互相垂直
3.如图,菱形ABCD对角线AC与BD交于点O,点E是DC边上的中点,连接OE,OE=5,BD=12,则菱形的面积为( )
A.96 B.48 C.192 D.24
4.菱形和矩形的对角线,具有的性质是下列的( )
A.对角线相等 B.对角线互相垂直
C.对角线互相垂直平分 D.对角线互相平分
5.在梯形纸片ABCD中,AD//BC,AD>CD.将纸片沿过点D的直线折叠,使点C落在AD边上的点C′处,折痕DE交BC于点E,连接C′E,则四边形CDC′E的形状准确地说应为().
A.矩形 B.菱形
C.梯形 D.平行四边形
6.如图,在平行四边形ABCD中对角线AC、BD交于点O,并且∠DAC=60°,∠ADB=15°.点E是AD边上一个动点,延长EO交BC于点F,当点E从D点向A点移动过程中(点E与点D,A不重合),则四边形AFCE的变化是( )
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→菱形→平行四边形→矩形→平行四边形
C.平行四边形→矩形→平行四边形→正方形→平行四边形
D.平行四边形→矩形→菱形→正方形→平行四边形
7.如图在矩形纸片中,,将矩形纸片折叠,使点与点重合,则折痕的长是( )
A. B. C. D.
8.某校的校园内有一个由两个相同的正六边形(边长为)围成的花坛,如图中的阴影部分所示,校方先要将这个花坛在原有的基础上扩建成一个如图所示区域,并在新扩充的部分种上草坪,则扩建后区域的周长为( )
A. B. C. D.
9.如图,在图1中,、、分别是等边 的边、、的中点,在图2中,,,分别是的边、、的中点,…,按此规律,则第n个图形中菱形的个数共有( )个.
A. B. C. D.
10.如图,在菱形中,对角线,相交于点,,,则下列选项错误的是( )
A. B. C. D.
二、填空题
11.已知一个菱形的周长是4,较长的对角线比较短的对角线长2,则这个菱形的面积是______.
12.如图,已知菱形的一个内角,对角线,相交于点,点在上,且,则________________.
13.菱形的两条对角线长分别为5和12,那么这个菱形的面积为___________
14.有两个全等矩形纸条,长与宽分别为11和7,按如图所示的方式交叉叠放在一起,则重合部分构成的四边形的周长为_______________.
15.如图,在菱形ABCD中,,∠BCD=60°,对角线AC、BD相交于点O,点E是OC上一点,连接ED,若,则DE的长为______.
三、解答题
16.如图,在中,点D、E分别是边BC、AC的中点,过点A作交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当满足什么条件时,四边形图ADCF是菱形?为什么?
17.如图,在四边形ABCD中,对角线AC,BD相交于点O,OA=OC,OB=OD,点E是BC延长线上一点,连接DE,DEAC,DE⊥BD,点D到BE的距离为d.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求d.
18.如图:在中,以点A为圆心,AB的长为半径画弧交AD于点F,再分别以点B,F为圆心,大于的长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是什么四边形?请说明理由;
(2)若四边形ABEF的周长为40,,求AE的长和的度数.
参考答案
1.C
【详解】解:在菱形中,∵,
∴,
∴,
∵,
∴,
故答案选C.
2.A
【详解】解:菱形的对角线互相平分、垂直、对角线平分一组对角,
矩形的对角线互相平分、相等,
∴矩形具有而菱形不具有的性质是对角线相等,
故选A.
3.A
【详解】∵四边形ABCD是菱形,
∴AC⊥BD,,,
∴CD=2OE=10,
∴,
∴AC=2OC=16,
∴菱形的面积为:.
故选A.
4.D
【详解】解:∵矩形的对角线相等且互相平分,菱形的对角线垂直且互相平分,
∴菱形和矩形的对角线,具有的相同性质是对角线互相平分,
故选:D.
5.B
【详解】四边形CDC′E是菱形.
理由:根据折叠的性质,可得:CD=C′D,∠C′DE=∠CDE,CE=C′E,
∵AD∥BC,
∴∠C′DE=∠CED,
∴∠CDE=∠CED,
∴CD=CE,
∴CD=C′D=C′E=CE,
∴四边形CDC′E为菱形.
故选B.
6.B
【详解】解:点E从D点向A点移动过程中,
∵四边形ABCD是平行四边形,
∴AD∥BC,AO=CO,
∴∠EAO=∠FCO,∠AEO=∠CFO,
∴△AOE≌△COF,
∴AE=CF,
∴四边形AECF是平行四边形;
∵∠AOD=180°-∠DAC-∠ADB=115°,
∴当∠EOD=15°时,∠AOE=90°,
此时平行四边形AECF是菱形;
当∠EOD=45°,∠AEO=∠EOD+∠ADO=45°+15°=60°,
∴∠OAE=∠OEA,
∴OA=OE,
∴AC=EF,
此时平行四边形AECF是矩形;
∴∠EOD<15°时,四边形AFCE为平行四边形,
当∠EOD=15°时,AC⊥EF,四边形AFCE为菱形,
当15°<∠EOD<45°时,四边形AFCE为平行四边形,
当∠EOD=45°时,四边形AFCE为矩形,
当45°<∠EOD<105°时,四边形AFCE为平行四边形,
故选:B.
7.C
【详解】解:连接BE,BD,设EF与BD
相交于点O,如图,
矩形ABCD纸片折叠,使点D与点B重合,
垂直平分BD,,
,
,
,
,
,
,
,
四边形DEBF为菱形,
在中,
,
设BE=x,则DE=x,AE=8-x,
在中,,
即,
解得,
,
S菱形DEBF=S三角形DEB,
,
,
,
故选:C.
8.B
【详解】解:如图,∵花坛是由两个相同的正六边形围成,
∴∠FGM=∠GMN=120°,GM=GF=EF,
∴∠BMG=∠BGM=60°,
∴△BMG是等边三角形,
∴BG=GM=1(m),
同理可证:AF=EF=1(m)
∴AB=BG+GF+AF=1×3=3(m),
∴扩建后菱形区域的周长为3×4=12(m),
故选:B.
9.C
【详解】解:由题意可得,
∵、、分别是等边 的边、、的中点,
∴ ,
∴图1有三个菱形,由此可得作一次中位线分三个菱形,
∴第n个图形中菱形的个数共有 个菱形,
故选C.
10.C
【详解】解:∵菱形
∴AB=BC=CE=AE,AC⊥BE,OE=BE
又∵,
∴四边形OCDE是矩形
∴OD=CE,OE=CD
∴OD=AB=AE,OB=CD
故A、B选项正确;
又∵
∴四边形OBCD是平行四边形
∴OD∥BC
所以D正确;
又OD=CE与BE没有直接关系,所以C错误;
故答案为C.
11.2
【详解】解:∵菱形的周长是4,
∴边长为,
∵较长的对角线比较短的对角线长2,,
∴设菱形的两对角线分别为x,(x+2),
根据菱形的性质可知,菱形的对角线互相垂直平分,
则对角线的一半分别为,,
根据勾股定理得,()2+()2=()2,
整理得:x(x+2)=4,
∴这个菱形的面积= x(x+2)=2.
故答案为:2.
12.
【详解】解:在菱形中,
∴,,
又∵
∴
∴
故答案为25.
13.30
【详解】解:∵菱形的两条对角线长分别为5和12,
∴菱形的面积:.
故答案为:30.
14.
【详解】由题意得矩形矩形,
,
∴四边形是平行四边形,
∴平行四边形的面积,
,∴四边形是菱形,
.
设,则.
在中,由勾股定理得,
解得
,
∴四边形的周长.
15.
【详解】解: 菱形ABCD,∠BCD=60°,,
故答案为:
16.
【详解】(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,BD=CD,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD,则AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)解:当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,
理由:∵△ABC是直角三角形,且∠BAC=90°
又∵点D是边BC的中点,
∴AD=DC,
∴平行四边形ADCF是菱形.
17.
【详解】(1)证明:∵OA=OC,OB=OD,
∴四边形 ABCD 是平行四边形.
∵DEAC,DE⊥BD,
∴ AC ⊥BD,
∴四边形 ABCD 是菱形.
(2)解:如图,过点D 作DF⊥BE ,垂足为点 F .
由(1)知,
在Rt△AOB 中.
∵四边形 ABCD 是菱形,
∴ BC =CD = AB = AD =5 ,BD =2OB =8 ,ADCE.
∵ DE/AC,
∴四边形 ACED 是平行四边形,
∴ CE = AD = 5 ,DE= AC = 6 ,
∴.
18.(1)四边形ABEF是菱形,理由见解析
(2)10,120°
【详解】解:(1)四边形ABEF是菱形.
理由:从尺规作图中得出AB=AF,∠BAE=∠FAE.
∵四边形ABCD是平行四边形,
∴AF∥BC,
∴∠FAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE.
∵AB=AF,
∴BE=AF.
又∵BE∥AF,
∴四边形ABEF是平行四边形.
由于AB=BE,
∴四边形ABEF是菱形.
(2)设BF与AE交于点O.
∵菱形ABEF的周长为40,
∴AF=AB=10.
又∵BF=10,
∴AF=AB=BF.
∴∠BAF=60°.
∵四边形ABEF是菱形,
∴AE⊥BF,OF=BF=5,AE=2AO,AF∥BC.
∴AO==,
∴AE=2AO=10.
∵AF∥BC,
∴∠ABC+∠BAF=180°,
∴∠ABC=180°-∠BAF=120°.
一、单选题
1.如图,在菱形中,过顶点作交对角线于点,已知,则的大小为( ).
A.20° B.25° C.65° D.75°
2.矩形具有而菱形不具有的性质是( )
A.对角线相等 B.对角线平分一组对角
C.对角线互相平分 D.对角线互相垂直
3.如图,菱形ABCD对角线AC与BD交于点O,点E是DC边上的中点,连接OE,OE=5,BD=12,则菱形的面积为( )
A.96 B.48 C.192 D.24
4.菱形和矩形的对角线,具有的性质是下列的( )
A.对角线相等 B.对角线互相垂直
C.对角线互相垂直平分 D.对角线互相平分
5.在梯形纸片ABCD中,AD//BC,AD>CD.将纸片沿过点D的直线折叠,使点C落在AD边上的点C′处,折痕DE交BC于点E,连接C′E,则四边形CDC′E的形状准确地说应为().
A.矩形 B.菱形
C.梯形 D.平行四边形
6.如图,在平行四边形ABCD中对角线AC、BD交于点O,并且∠DAC=60°,∠ADB=15°.点E是AD边上一个动点,延长EO交BC于点F,当点E从D点向A点移动过程中(点E与点D,A不重合),则四边形AFCE的变化是( )
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→菱形→平行四边形→矩形→平行四边形
C.平行四边形→矩形→平行四边形→正方形→平行四边形
D.平行四边形→矩形→菱形→正方形→平行四边形
7.如图在矩形纸片中,,将矩形纸片折叠,使点与点重合,则折痕的长是( )
A. B. C. D.
8.某校的校园内有一个由两个相同的正六边形(边长为)围成的花坛,如图中的阴影部分所示,校方先要将这个花坛在原有的基础上扩建成一个如图所示区域,并在新扩充的部分种上草坪,则扩建后区域的周长为( )
A. B. C. D.
9.如图,在图1中,、、分别是等边 的边、、的中点,在图2中,,,分别是的边、、的中点,…,按此规律,则第n个图形中菱形的个数共有( )个.
A. B. C. D.
10.如图,在菱形中,对角线,相交于点,,,则下列选项错误的是( )
A. B. C. D.
二、填空题
11.已知一个菱形的周长是4,较长的对角线比较短的对角线长2,则这个菱形的面积是______.
12.如图,已知菱形的一个内角,对角线,相交于点,点在上,且,则________________.
13.菱形的两条对角线长分别为5和12,那么这个菱形的面积为___________
14.有两个全等矩形纸条,长与宽分别为11和7,按如图所示的方式交叉叠放在一起,则重合部分构成的四边形的周长为_______________.
15.如图,在菱形ABCD中,,∠BCD=60°,对角线AC、BD相交于点O,点E是OC上一点,连接ED,若,则DE的长为______.
三、解答题
16.如图,在中,点D、E分别是边BC、AC的中点,过点A作交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当满足什么条件时,四边形图ADCF是菱形?为什么?
17.如图,在四边形ABCD中,对角线AC,BD相交于点O,OA=OC,OB=OD,点E是BC延长线上一点,连接DE,DEAC,DE⊥BD,点D到BE的距离为d.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求d.
18.如图:在中,以点A为圆心,AB的长为半径画弧交AD于点F,再分别以点B,F为圆心,大于的长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是什么四边形?请说明理由;
(2)若四边形ABEF的周长为40,,求AE的长和的度数.
参考答案
1.C
【详解】解:在菱形中,∵,
∴,
∴,
∵,
∴,
故答案选C.
2.A
【详解】解:菱形的对角线互相平分、垂直、对角线平分一组对角,
矩形的对角线互相平分、相等,
∴矩形具有而菱形不具有的性质是对角线相等,
故选A.
3.A
【详解】∵四边形ABCD是菱形,
∴AC⊥BD,,,
∴CD=2OE=10,
∴,
∴AC=2OC=16,
∴菱形的面积为:.
故选A.
4.D
【详解】解:∵矩形的对角线相等且互相平分,菱形的对角线垂直且互相平分,
∴菱形和矩形的对角线,具有的相同性质是对角线互相平分,
故选:D.
5.B
【详解】四边形CDC′E是菱形.
理由:根据折叠的性质,可得:CD=C′D,∠C′DE=∠CDE,CE=C′E,
∵AD∥BC,
∴∠C′DE=∠CED,
∴∠CDE=∠CED,
∴CD=CE,
∴CD=C′D=C′E=CE,
∴四边形CDC′E为菱形.
故选B.
6.B
【详解】解:点E从D点向A点移动过程中,
∵四边形ABCD是平行四边形,
∴AD∥BC,AO=CO,
∴∠EAO=∠FCO,∠AEO=∠CFO,
∴△AOE≌△COF,
∴AE=CF,
∴四边形AECF是平行四边形;
∵∠AOD=180°-∠DAC-∠ADB=115°,
∴当∠EOD=15°时,∠AOE=90°,
此时平行四边形AECF是菱形;
当∠EOD=45°,∠AEO=∠EOD+∠ADO=45°+15°=60°,
∴∠OAE=∠OEA,
∴OA=OE,
∴AC=EF,
此时平行四边形AECF是矩形;
∴∠EOD<15°时,四边形AFCE为平行四边形,
当∠EOD=15°时,AC⊥EF,四边形AFCE为菱形,
当15°<∠EOD<45°时,四边形AFCE为平行四边形,
当∠EOD=45°时,四边形AFCE为矩形,
当45°<∠EOD<105°时,四边形AFCE为平行四边形,
故选:B.
7.C
【详解】解:连接BE,BD,设EF与BD
相交于点O,如图,
矩形ABCD纸片折叠,使点D与点B重合,
垂直平分BD,,
,
,
,
,
,
,
,
四边形DEBF为菱形,
在中,
,
设BE=x,则DE=x,AE=8-x,
在中,,
即,
解得,
,
S菱形DEBF=S三角形DEB,
,
,
,
故选:C.
8.B
【详解】解:如图,∵花坛是由两个相同的正六边形围成,
∴∠FGM=∠GMN=120°,GM=GF=EF,
∴∠BMG=∠BGM=60°,
∴△BMG是等边三角形,
∴BG=GM=1(m),
同理可证:AF=EF=1(m)
∴AB=BG+GF+AF=1×3=3(m),
∴扩建后菱形区域的周长为3×4=12(m),
故选:B.
9.C
【详解】解:由题意可得,
∵、、分别是等边 的边、、的中点,
∴ ,
∴图1有三个菱形,由此可得作一次中位线分三个菱形,
∴第n个图形中菱形的个数共有 个菱形,
故选C.
10.C
【详解】解:∵菱形
∴AB=BC=CE=AE,AC⊥BE,OE=BE
又∵,
∴四边形OCDE是矩形
∴OD=CE,OE=CD
∴OD=AB=AE,OB=CD
故A、B选项正确;
又∵
∴四边形OBCD是平行四边形
∴OD∥BC
所以D正确;
又OD=CE与BE没有直接关系,所以C错误;
故答案为C.
11.2
【详解】解:∵菱形的周长是4,
∴边长为,
∵较长的对角线比较短的对角线长2,,
∴设菱形的两对角线分别为x,(x+2),
根据菱形的性质可知,菱形的对角线互相垂直平分,
则对角线的一半分别为,,
根据勾股定理得,()2+()2=()2,
整理得:x(x+2)=4,
∴这个菱形的面积= x(x+2)=2.
故答案为:2.
12.
【详解】解:在菱形中,
∴,,
又∵
∴
∴
故答案为25.
13.30
【详解】解:∵菱形的两条对角线长分别为5和12,
∴菱形的面积:.
故答案为:30.
14.
【详解】由题意得矩形矩形,
,
∴四边形是平行四边形,
∴平行四边形的面积,
,∴四边形是菱形,
.
设,则.
在中,由勾股定理得,
解得
,
∴四边形的周长.
15.
【详解】解: 菱形ABCD,∠BCD=60°,,
故答案为:
16.
【详解】(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,BD=CD,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD,则AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)解:当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,
理由:∵△ABC是直角三角形,且∠BAC=90°
又∵点D是边BC的中点,
∴AD=DC,
∴平行四边形ADCF是菱形.
17.
【详解】(1)证明:∵OA=OC,OB=OD,
∴四边形 ABCD 是平行四边形.
∵DEAC,DE⊥BD,
∴ AC ⊥BD,
∴四边形 ABCD 是菱形.
(2)解:如图,过点D 作DF⊥BE ,垂足为点 F .
由(1)知,
在Rt△AOB 中.
∵四边形 ABCD 是菱形,
∴ BC =CD = AB = AD =5 ,BD =2OB =8 ,ADCE.
∵ DE/AC,
∴四边形 ACED 是平行四边形,
∴ CE = AD = 5 ,DE= AC = 6 ,
∴.
18.(1)四边形ABEF是菱形,理由见解析
(2)10,120°
【详解】解:(1)四边形ABEF是菱形.
理由:从尺规作图中得出AB=AF,∠BAE=∠FAE.
∵四边形ABCD是平行四边形,
∴AF∥BC,
∴∠FAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE.
∵AB=AF,
∴BE=AF.
又∵BE∥AF,
∴四边形ABEF是平行四边形.
由于AB=BE,
∴四边形ABEF是菱形.
(2)设BF与AE交于点O.
∵菱形ABEF的周长为40,
∴AF=AB=10.
又∵BF=10,
∴AF=AB=BF.
∴∠BAF=60°.
∵四边形ABEF是菱形,
∴AE⊥BF,OF=BF=5,AE=2AO,AF∥BC.
∴AO==,
∴AE=2AO=10.
∵AF∥BC,
∴∠ABC+∠BAF=180°,
∴∠ABC=180°-∠BAF=120°.
