第四单元比例高频考点检测卷(单元测试) 小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 第四单元比例高频考点检测卷(单元测试) 小学数学六年级下册苏教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第四单元比例高频考点检测卷(单元测试)-小学数学六年级下册苏教版
一、选择题
1.能与3∶组成比例的是( )。
A.4∶3 B.3∶4 C.∶3 D.4∶
2.3a=4b,a∶b=( )。
A.3∶4 B.4∶3 C.1∶1 D.4∶1
3.把线段比例尺改写成数值比例尺是( )。
A.l∶10 B.l∶1000000 C.l∶3000000 D.l∶2000000
4.把一个边长是4厘米的正方形按的比例放大,放大后的正方形的面积是( )平方厘米。
A.8 B.16 C.64 D.32
5.黄桥小学教育集团新城校区南北长360米,东西长96米,设计师想把学校的平面图画在一张长20厘米,宽12厘米长方形纸上。选择( )比较合适。
A.1∶600 B.1∶800 C.1∶1800 D.1∶2000
6.有两个底面积相等的圆柱,第一个圆柱与第二个圆柱的高之比是5∶8,第二个圆柱的体积是120立方分米,则第一个圆柱的体积是( )立方分米。
A.60 B.70 C.75 D.80
二、填空题
7.24因数有( ),从中选4个不同的数组成比例是( )。
8.甲数的等于乙数的(甲、乙不为0),那么甲数与乙数的比是( ),甲数是两数和的。
9.在比例尺是1∶100的图纸上,甲乙两个圆半径的比是3∶7,那么甲乙两个圆实际半径的比是( )∶( ),实际面积的比是( )∶( )。
10.两地相距36千米,在一幅地图上的距离是12厘米,这幅地图的比例尺是( ),在这幅地图上量得甲乙两地相距8厘米,甲乙两地的实际距离是( )千米。
11.希望小学有一块长方形农耕园,在比例尺是1∶1000的校园平面图上量得农耕园的长是5厘米,宽是2厘米。这块农耕园的实际面积是( )平方米。
12.一幅平面图的比例尺是1∶500,表示实际距离是图上距离的( )倍,图上距离是实际距离的( )。
13.机器零件长1.5毫米,画在图上是3厘米,比例尺是( )。
14.王老师用扇形统计图反映新星小学的学生和老师情况,表示男生和女生的扇形圆心角度数比是6∶5,表示老师的扇形圆心角度数是30°。已知老师有50人,新星小学有女生( )人。
三、判断题
15.如果3x=5y,那么x∶y=5∶3。( )
16.一幅地图的比例尺是,表示图上面积与实际面积的比是1∶600。( )
17.把一个圆按3∶1的比放大后,两个圆的周长比和面积比能组成比例。( )
18.交换比例的两个外项,比例仍然成立。( )
19.如果ab = cd,那么=。( )
四、计算题
20.解方程
五、解答题
21.妈妈用800克雪梨和2000克水制作雪梨汤,口感极好。红红准备了960克雪梨,要和妈妈做的口感相同,她要用水多少克?(用比例解)
22.李奶奶家养鸡100只,其中公鸡占母鸡只数的。李奶奶家养公鸡和母鸡各多少只?(用两种方法解答)
23.在一幅比例尺为1∶3000000的地图上量得两地间的距离是5厘米,两地实际相距多少千米?
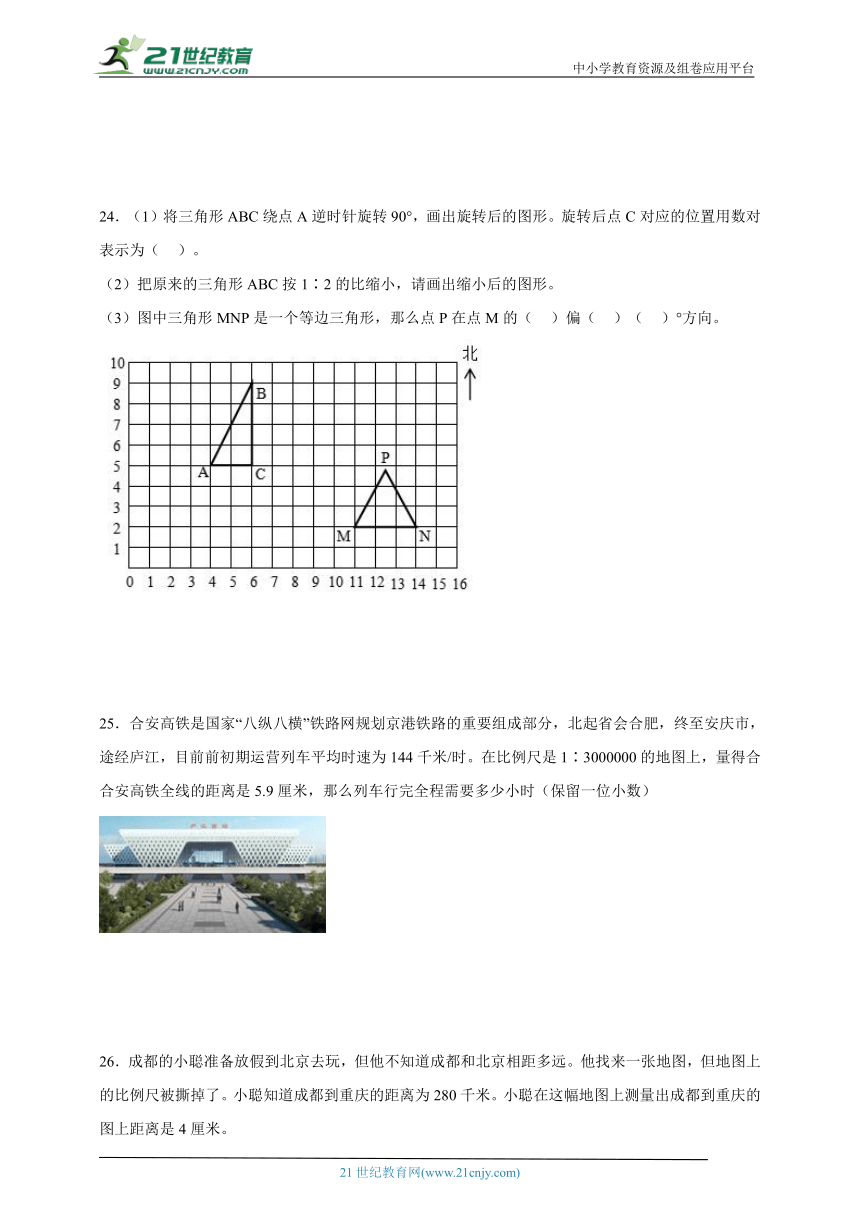
24.(1)将三角形ABC绕点A逆时针旋转90°,画出旋转后的图形。旋转后点C对应的位置用数对表示为( )。
(2)把原来的三角形ABC按1∶2的比缩小,请画出缩小后的图形。
(3)图中三角形MNP是一个等边三角形,那么点P在点M的( )偏( )( )°方向。
25.合安高铁是国家“八纵八横”铁路网规划京港铁路的重要组成部分,北起省会合肥,终至安庆市,途经庐江,目前前初期运营列车平均时速为144千米/时。在比例尺是1∶3000000的地图上,量得合合安高铁全线的距离是5.9厘米,那么列车行完全程需要多少小时(保留一位小数)
26.成都的小聪准备放假到北京去玩,但他不知道成都和北京相距多远。他找来一张地图,但地图上的比例尺被撕掉了。小聪知道成都到重庆的距离为280千米。小聪在这幅地图上测量出成都到重庆的图上距离是4厘米。
(1)这幅地图的比例尺是多少?
(2)成都到北京的图上距离是30厘米。你能算出成都到北京的实际距离约是多少吗?
参考答案:
1.D
【分析】表示两个比相等的式子叫做比例,分别求出3∶与各选项的比值,找出比值相等的即可。
【详解】3∶=3÷=12
4∶3=4÷3=
3∶4=3÷4=
∶3=÷3=
4∶=4÷=12
所以能与3∶组成比例的是4∶。
故答案为:D
【点睛】本题主要考查比例的意义。
2.B
【分析】根据比例的性质,把所给的等式3a=4b改写成一个外项是a,一个内项是b的比例,则和a相乘的数3就作为比例的另一个外项,和b相乘的数4就作为比例的另一个内项,据此写出比例即可。
【详解】因为3a=4b,所以a∶b=4∶3;
故选:B。
【点睛】此题考查把给出的等式改写成比例式,在改写时,要注意:相乘的两个数要做内项就都做内项,要做外项就都做外项。
3.B
【分析】根据比例尺的定义,先把10千米化为1000000厘米,然后用数值比例尺表示即可。
【详解】图上1厘米表示实际10千米,10千米=1000000厘米
数值比例尺是:1:1000000
故答案为:B
【点睛】本题考查了比例线段,掌握比例尺的定义是解题的关键,注意单位的换算问题。
4.C
【分析】根据比例将边长是4厘米的正方形按2∶1放大,扩大后的正方形的边长是:4×2=8厘米,根据正方形面积公式:边长×边长,放大后的正方形面积是:8×8,即可解答。
【详解】放大后正方形边长:4×2=8(厘米)
放大后的正方形面积是:8×8=64(平方厘米)
故答案为:C
【点睛】本题考查对图形按比例扩大的理解和正方形面积公式的应用。
5.C
【分析】比例尺=图上距离∶实际距离,根据题意可直接求得比例尺再选择。
【详解】360米=36000厘米
96米=9600厘米
20∶36000=1∶1800
12∶9600=1∶800
选择1∶1800的比例尺合适。
故答案为:C
【点睛】考查了比例尺的概念,掌握比例尺的计算方法,注意在求比的过程中,单位要统一。
6.C
【分析】根据题意,圆柱的体积是:底面积×高,两个底面积相等的圆柱,那么它们的体积比就等于圆柱的高的比,第一个圆柱的高与第二个圆柱的高的比是5∶8,第一个圆柱∶第二个圆柱=5∶8,第二个圆柱的体积是120立方分米,设第一个圆柱的体积为x立方分米,列出比列式,解答即可。
【详解】解:设第一个圆柱的体积为x立方分米
5∶8=x∶120
8x=120×5
8x=600
x=600÷8
x=75
故答案选:C
【点睛】本题的关键是确定两个底面积相等的圆柱,高的比等于圆柱体积的比,进行计算即可。
7. 1、2、3、4、6、8、12、24 1∶2=12∶24
【分析】找出24的所有因数,根据比例的基本性质,两内项积等于两外项积,找出乘积是24的两对因数分别作比例的内项和外项即可。
【详解】24的因数有:1、2、3、4、6、8、12、24,组成的比例是1∶2=12∶24。(第二问答案不唯一)
【点睛】此题主要考查了比例的基本性质,学会灵活运用。也可根据比例的意义解答。
8.21∶8;
【分析】根据题意可知,甲数的等于乙数的 ,即:×甲数=×乙数,根据比例的基本性质:内项积等于外项积,可以推出甲数∶乙数=∶,化简即可;甲数是两数和的几分之几,根据甲数∶乙数=∶,用÷(+),即可解答。
【详解】×甲数=×乙数
甲数∶乙数=∶
=×
=
=21∶8
甲数÷(甲数+乙数)=÷(+)
=÷(+)
=÷
=×
=
【点睛】本题考查比例的基本性质及求一个数占另一个数的几分之几。
9. 3 7 9 49
【分析】根据比例尺的意义,令甲乙两圆的图上半径为3r,7r,根据比例尺可得实际圆的半径分别是300r,700r,进一步得出半径的比,然后根据圆的面积=πr ,即可得出甲、乙两个圆的实际的面积比。
【详解】设:甲乙两圆的图上半径分别为3r,7r;则甲乙两圆的实际半径为300r,700r。
所以甲乙两个圆实际半径的比是:300r∶700r=3∶7。
实际面积的比是:
(π300r×300r)∶(π700r×700r)=9∶49
【点睛】解答此题的关键是理解图上距离、实际距离、和比例尺的关系,以及圆的面积公式。
10. 1∶300000 24
【分析】根据题意,已知实际距离和图上距离,依据“比例尺=图上距离∶实际距离”,即可求出比例尺;图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”,即可求出两地的实际距离。
【详解】36千米=3600000厘米
比例尺:12∶3600000=1∶300000
实际距离:8÷
=8×300000
=2400000(厘米)
2400000厘米=24千米
【点睛】本题考查比例尺的意义以及图上距离、实际距离和比例尺的关系。
11.1000
【分析】实际距离=图上距离÷比例尺,据此求出农耕园的实际长与宽,进而求出长方形的面积。
【详解】5÷ =5000(厘米),5000厘米=50米;
2÷=2000(厘米),2000厘米=20米;
50×20=1000(平方米)
这块农耕园的实际面积是1000平方米。
【点睛】此题考查了图上距离与实际距离的换算,注意先求出对应边的长与宽,再解答。
12. 500
【分析】根据比例尺=图上距离∶实际距离,解答即可。
【详解】图上距离∶实际距离=1∶500,所以实际距离是图上距离的500倍,图上距离是实际距离的。
【点睛】此题考查了比例尺的意义。
13.20∶1
【解析】实际距离是1.5毫米,图上距离是3厘米,也就是30毫米,图上距离与实际距离的比即为比例尺。
【详解】3厘米=30毫米
30毫米∶1.5毫米=20∶1
所以这幅图的比例尺是20∶1。
【点睛】比例尺指的是图上距离与实际距离的比,注意顺序,求比例尺的时候注意单位换算。
14.250
【分析】由题意知:表示老师的扇形圆心角度数是30°,占整个扇形的30÷360=,老师有50人,50人对应着分率,从而求得整个扇形表示的总人数,进而求得女生人数点扇形的比率,用总人数乘女生比率,本题得解。据此解答。
【详解】老师人数占扇形的比率:30÷360=
师生总人数:50÷=600(人)
女生占扇形的比率:(360-30)×÷360
=150÷360
=
女生人数:600×=250(人)
【点睛】求得女生人数在扇形中的比率是解答本题的关键。
15.√
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
【详解】根据题意可知,x和3为外项,y和5为内项,那么x∶y=5∶3。
故答案为:√
【点睛】应用比例的基本性质是解答此题的关键。
16.×
【分析】根据比例尺的意义,即比例尺表示图上距离与实际距离的比,而不是图上面积与实际面积的比。
【详解】一幅地图的比例尺是,表示图上距离与实际距离的比是1∶600。
故答案为:×
【点睛】这道题主要考查学生对比例尺的意义的理解,明确是距离而不是面积。
17.×
【分析】设原来圆的半径是1,根据圆周长公式:和圆面积公式:,然后根据比例的意义即可判断。
【详解】假设原来圆的半径是1,放大后的半径为3。
周长比:(2×π×1)∶(2×π×3)=1∶3
面积比:(π×1)∶(π×3)=1∶9
通过比对,两个比的比值不相等,所以不能组成比例。
所以答案是:×
【点睛】此题考查了学生对圆的周长和面积公式的应用。
18.√
【分析】依据比例的基本性质,即两个内项之积等于两个外项之积,即可进行判断。
【详解】在一个比例中,两个外项交换位置后,两个内项之积仍然等于两个外项之积,所以仍是比例。例如:2∶3=4∶6,6∶3=4∶2。
故答案为:√
【点睛】此题主要考查比例的基本性质,解答时可以举例证明。
19.×
【分析】抓住“0”这个特殊的数,a、b、c、d应有个取值范围,因为0不能做除数,所以原题说法错误。
【详解】在这个式子中,是用字母a、b、c、d来表示数的,因为除数不能为0,所以a、b、c、d应有个取值范围,也就是:它们应该都是非0的数才能成立,原题题干不严谨。
故答案为:×
【点睛】此题关键在于通过数学语言和结论的严谨性来判断,0不能做除数和分母。
20.;;
【分析】根据等式的性质解方程即可。
(1)先算得,等式两边再同时乘;
(2)根据比例的基本性质,把比例转化成方程,等式两边再同时乘;
(3)等式两边先同时加上4.2,再同时乘。
【详解】(1)
解:=35
x=30
(2)
解:
x=
(3)
解:
x=16.5
21.2400克
【分析】设要用水x克,妈妈用800克雪梨和2000克水制作雪梨汤,口感极好,即雪梨的克数和水的克数比不变;根据比例的意义,960克雪梨∶x克水的比值等于800克雪梨∶2000克水,列方程:960∶x=800∶2000,解比例,即可解答。
【详解】解:设她要用水x克
960∶x=800∶2000
800x=960×2000
800x=1920000
x=2400
答:她要用水2400克。
【点睛】本题考查比例的意义,根据比例的意义列比例,解比例,进行解答。
22.公鸡20只;母鸡80只
【分析】方法1:公鸡占母鸡只数的,相当于把100只鸡平均分成5份,公鸡占1份,母鸡占4份,用100×求出公鸡数量,用100×求出母鸡数量。
方法2:设公鸡数量为x只,母鸡数量为(100-x)只。用x∶(100-x)=,解答即可。
【详解】由分析可知:
方法1:公鸡数量:100×=20(只)
母鸡数量:100×(1-)
=100×
=80(只)
方法2:解:设公鸡数量为x只,母鸡数量为(100-x)只。
x∶(100-x)=
100-x=4x
5x=100
x=20
母鸡:100-20=80(只)
答:李奶奶养公鸡20只,母鸡80只。
【点睛】此题主要考查学生对比例的理解与应用。
23.150千米
【分析】根据比例尺=图上距离∶实际距离;实际距离=图上距离÷比例尺,代入数据,即可解答。
【详解】5÷
=5×3000000
=15000000(厘米)
15000000厘米=150(千米)
答:两地实际相距150千米。
【点睛】本题考查比例尺的应用,解答本题的关键是掌握比例尺中的数量关系式。
24.(1)(4,7);图见详解;
(2)见详解;
(3)东;北;60
【分析】(1)将三角形ABC绕点A逆时针旋转90°后,A点位置不变,C点旋转到(4,7),B点旋转到(0,7),连接旋转后的B点和A点即成三角形ABC绕点A逆时针旋转90°后的图形;
(2)原来的三角形ABC两条直角分别为2格和4格,按1∶2缩小后两条直角边分别为1格和2格,先画出两边直角边,再连接出斜边即可;
(3)以M为观测点,MN在正东方,三角形MNP是等边三角形,则∠PMN是60°,据此可判断P点的方向。
【详解】画图如下:
(1)三角形ABC绕点A逆时针旋转90°后的图形如上图,旋转后点C对应的位置用数对表示为(4,7);
(2)三角形ABC按1∶2的比缩小后的图形如上图;
(3)P点在M点的东偏北60°方向上。
【点睛】此题重点考查平面图形旋转和缩小的方法,以及以数对确定位置、以正方向加偏转角度确定方向的方法。
25.1.2小时
【分析】图上距离和比例尺已知,依据“图上距离÷比例尺=实际距离”即可求出两地的实际距离。再根据“时间=路程÷速度”即可求出。
【详解】5.9÷=17700000(厘米)
17700000厘米=177千米
177÷144≈1.2(小时)
答:列车行完全程需要1.2小时。
【点睛】此题主要考查图上距离、实际距离和比例尺之间的关系,以及行程问题中的基本数量关系“时间=路程÷速度”。
26.(1)1∶7000000;(2)2100千米
【分析】(1)图上距离∶实际距离=比例尺。据此先统一单位再解答。
(2)根据(1)题中求出的这幅地图的比例尺,得出图上1厘米的距离表示实际多少千米,再乘30即可解答。
【详解】(1)280千米=28000000厘米
4∶28000000=1∶7000000
答:这幅地图的比例尺是1∶7000000。
(2)7000000=70千米
70×30=2100(千米)
答:成都到北京的实际距离约是2100千米。
【点睛】本题考查比例尺的应用。根据比例尺的意义明确图上1厘米的距离表示实际多少千米是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四单元比例高频考点检测卷(单元测试)-小学数学六年级下册苏教版
一、选择题
1.能与3∶组成比例的是( )。
A.4∶3 B.3∶4 C.∶3 D.4∶
2.3a=4b,a∶b=( )。
A.3∶4 B.4∶3 C.1∶1 D.4∶1
3.把线段比例尺改写成数值比例尺是( )。
A.l∶10 B.l∶1000000 C.l∶3000000 D.l∶2000000
4.把一个边长是4厘米的正方形按的比例放大,放大后的正方形的面积是( )平方厘米。
A.8 B.16 C.64 D.32
5.黄桥小学教育集团新城校区南北长360米,东西长96米,设计师想把学校的平面图画在一张长20厘米,宽12厘米长方形纸上。选择( )比较合适。
A.1∶600 B.1∶800 C.1∶1800 D.1∶2000
6.有两个底面积相等的圆柱,第一个圆柱与第二个圆柱的高之比是5∶8,第二个圆柱的体积是120立方分米,则第一个圆柱的体积是( )立方分米。
A.60 B.70 C.75 D.80
二、填空题
7.24因数有( ),从中选4个不同的数组成比例是( )。
8.甲数的等于乙数的(甲、乙不为0),那么甲数与乙数的比是( ),甲数是两数和的。
9.在比例尺是1∶100的图纸上,甲乙两个圆半径的比是3∶7,那么甲乙两个圆实际半径的比是( )∶( ),实际面积的比是( )∶( )。
10.两地相距36千米,在一幅地图上的距离是12厘米,这幅地图的比例尺是( ),在这幅地图上量得甲乙两地相距8厘米,甲乙两地的实际距离是( )千米。
11.希望小学有一块长方形农耕园,在比例尺是1∶1000的校园平面图上量得农耕园的长是5厘米,宽是2厘米。这块农耕园的实际面积是( )平方米。
12.一幅平面图的比例尺是1∶500,表示实际距离是图上距离的( )倍,图上距离是实际距离的( )。
13.机器零件长1.5毫米,画在图上是3厘米,比例尺是( )。
14.王老师用扇形统计图反映新星小学的学生和老师情况,表示男生和女生的扇形圆心角度数比是6∶5,表示老师的扇形圆心角度数是30°。已知老师有50人,新星小学有女生( )人。
三、判断题
15.如果3x=5y,那么x∶y=5∶3。( )
16.一幅地图的比例尺是,表示图上面积与实际面积的比是1∶600。( )
17.把一个圆按3∶1的比放大后,两个圆的周长比和面积比能组成比例。( )
18.交换比例的两个外项,比例仍然成立。( )
19.如果ab = cd,那么=。( )
四、计算题
20.解方程
五、解答题
21.妈妈用800克雪梨和2000克水制作雪梨汤,口感极好。红红准备了960克雪梨,要和妈妈做的口感相同,她要用水多少克?(用比例解)
22.李奶奶家养鸡100只,其中公鸡占母鸡只数的。李奶奶家养公鸡和母鸡各多少只?(用两种方法解答)
23.在一幅比例尺为1∶3000000的地图上量得两地间的距离是5厘米,两地实际相距多少千米?
24.(1)将三角形ABC绕点A逆时针旋转90°,画出旋转后的图形。旋转后点C对应的位置用数对表示为( )。
(2)把原来的三角形ABC按1∶2的比缩小,请画出缩小后的图形。
(3)图中三角形MNP是一个等边三角形,那么点P在点M的( )偏( )( )°方向。
25.合安高铁是国家“八纵八横”铁路网规划京港铁路的重要组成部分,北起省会合肥,终至安庆市,途经庐江,目前前初期运营列车平均时速为144千米/时。在比例尺是1∶3000000的地图上,量得合合安高铁全线的距离是5.9厘米,那么列车行完全程需要多少小时(保留一位小数)
26.成都的小聪准备放假到北京去玩,但他不知道成都和北京相距多远。他找来一张地图,但地图上的比例尺被撕掉了。小聪知道成都到重庆的距离为280千米。小聪在这幅地图上测量出成都到重庆的图上距离是4厘米。
(1)这幅地图的比例尺是多少?
(2)成都到北京的图上距离是30厘米。你能算出成都到北京的实际距离约是多少吗?
参考答案:
1.D
【分析】表示两个比相等的式子叫做比例,分别求出3∶与各选项的比值,找出比值相等的即可。
【详解】3∶=3÷=12
4∶3=4÷3=
3∶4=3÷4=
∶3=÷3=
4∶=4÷=12
所以能与3∶组成比例的是4∶。
故答案为:D
【点睛】本题主要考查比例的意义。
2.B
【分析】根据比例的性质,把所给的等式3a=4b改写成一个外项是a,一个内项是b的比例,则和a相乘的数3就作为比例的另一个外项,和b相乘的数4就作为比例的另一个内项,据此写出比例即可。
【详解】因为3a=4b,所以a∶b=4∶3;
故选:B。
【点睛】此题考查把给出的等式改写成比例式,在改写时,要注意:相乘的两个数要做内项就都做内项,要做外项就都做外项。
3.B
【分析】根据比例尺的定义,先把10千米化为1000000厘米,然后用数值比例尺表示即可。
【详解】图上1厘米表示实际10千米,10千米=1000000厘米
数值比例尺是:1:1000000
故答案为:B
【点睛】本题考查了比例线段,掌握比例尺的定义是解题的关键,注意单位的换算问题。
4.C
【分析】根据比例将边长是4厘米的正方形按2∶1放大,扩大后的正方形的边长是:4×2=8厘米,根据正方形面积公式:边长×边长,放大后的正方形面积是:8×8,即可解答。
【详解】放大后正方形边长:4×2=8(厘米)
放大后的正方形面积是:8×8=64(平方厘米)
故答案为:C
【点睛】本题考查对图形按比例扩大的理解和正方形面积公式的应用。
5.C
【分析】比例尺=图上距离∶实际距离,根据题意可直接求得比例尺再选择。
【详解】360米=36000厘米
96米=9600厘米
20∶36000=1∶1800
12∶9600=1∶800
选择1∶1800的比例尺合适。
故答案为:C
【点睛】考查了比例尺的概念,掌握比例尺的计算方法,注意在求比的过程中,单位要统一。
6.C
【分析】根据题意,圆柱的体积是:底面积×高,两个底面积相等的圆柱,那么它们的体积比就等于圆柱的高的比,第一个圆柱的高与第二个圆柱的高的比是5∶8,第一个圆柱∶第二个圆柱=5∶8,第二个圆柱的体积是120立方分米,设第一个圆柱的体积为x立方分米,列出比列式,解答即可。
【详解】解:设第一个圆柱的体积为x立方分米
5∶8=x∶120
8x=120×5
8x=600
x=600÷8
x=75
故答案选:C
【点睛】本题的关键是确定两个底面积相等的圆柱,高的比等于圆柱体积的比,进行计算即可。
7. 1、2、3、4、6、8、12、24 1∶2=12∶24
【分析】找出24的所有因数,根据比例的基本性质,两内项积等于两外项积,找出乘积是24的两对因数分别作比例的内项和外项即可。
【详解】24的因数有:1、2、3、4、6、8、12、24,组成的比例是1∶2=12∶24。(第二问答案不唯一)
【点睛】此题主要考查了比例的基本性质,学会灵活运用。也可根据比例的意义解答。
8.21∶8;
【分析】根据题意可知,甲数的等于乙数的 ,即:×甲数=×乙数,根据比例的基本性质:内项积等于外项积,可以推出甲数∶乙数=∶,化简即可;甲数是两数和的几分之几,根据甲数∶乙数=∶,用÷(+),即可解答。
【详解】×甲数=×乙数
甲数∶乙数=∶
=×
=
=21∶8
甲数÷(甲数+乙数)=÷(+)
=÷(+)
=÷
=×
=
【点睛】本题考查比例的基本性质及求一个数占另一个数的几分之几。
9. 3 7 9 49
【分析】根据比例尺的意义,令甲乙两圆的图上半径为3r,7r,根据比例尺可得实际圆的半径分别是300r,700r,进一步得出半径的比,然后根据圆的面积=πr ,即可得出甲、乙两个圆的实际的面积比。
【详解】设:甲乙两圆的图上半径分别为3r,7r;则甲乙两圆的实际半径为300r,700r。
所以甲乙两个圆实际半径的比是:300r∶700r=3∶7。
实际面积的比是:
(π300r×300r)∶(π700r×700r)=9∶49
【点睛】解答此题的关键是理解图上距离、实际距离、和比例尺的关系,以及圆的面积公式。
10. 1∶300000 24
【分析】根据题意,已知实际距离和图上距离,依据“比例尺=图上距离∶实际距离”,即可求出比例尺;图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”,即可求出两地的实际距离。
【详解】36千米=3600000厘米
比例尺:12∶3600000=1∶300000
实际距离:8÷
=8×300000
=2400000(厘米)
2400000厘米=24千米
【点睛】本题考查比例尺的意义以及图上距离、实际距离和比例尺的关系。
11.1000
【分析】实际距离=图上距离÷比例尺,据此求出农耕园的实际长与宽,进而求出长方形的面积。
【详解】5÷ =5000(厘米),5000厘米=50米;
2÷=2000(厘米),2000厘米=20米;
50×20=1000(平方米)
这块农耕园的实际面积是1000平方米。
【点睛】此题考查了图上距离与实际距离的换算,注意先求出对应边的长与宽,再解答。
12. 500
【分析】根据比例尺=图上距离∶实际距离,解答即可。
【详解】图上距离∶实际距离=1∶500,所以实际距离是图上距离的500倍,图上距离是实际距离的。
【点睛】此题考查了比例尺的意义。
13.20∶1
【解析】实际距离是1.5毫米,图上距离是3厘米,也就是30毫米,图上距离与实际距离的比即为比例尺。
【详解】3厘米=30毫米
30毫米∶1.5毫米=20∶1
所以这幅图的比例尺是20∶1。
【点睛】比例尺指的是图上距离与实际距离的比,注意顺序,求比例尺的时候注意单位换算。
14.250
【分析】由题意知:表示老师的扇形圆心角度数是30°,占整个扇形的30÷360=,老师有50人,50人对应着分率,从而求得整个扇形表示的总人数,进而求得女生人数点扇形的比率,用总人数乘女生比率,本题得解。据此解答。
【详解】老师人数占扇形的比率:30÷360=
师生总人数:50÷=600(人)
女生占扇形的比率:(360-30)×÷360
=150÷360
=
女生人数:600×=250(人)
【点睛】求得女生人数在扇形中的比率是解答本题的关键。
15.√
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
【详解】根据题意可知,x和3为外项,y和5为内项,那么x∶y=5∶3。
故答案为:√
【点睛】应用比例的基本性质是解答此题的关键。
16.×
【分析】根据比例尺的意义,即比例尺表示图上距离与实际距离的比,而不是图上面积与实际面积的比。
【详解】一幅地图的比例尺是,表示图上距离与实际距离的比是1∶600。
故答案为:×
【点睛】这道题主要考查学生对比例尺的意义的理解,明确是距离而不是面积。
17.×
【分析】设原来圆的半径是1,根据圆周长公式:和圆面积公式:,然后根据比例的意义即可判断。
【详解】假设原来圆的半径是1,放大后的半径为3。
周长比:(2×π×1)∶(2×π×3)=1∶3
面积比:(π×1)∶(π×3)=1∶9
通过比对,两个比的比值不相等,所以不能组成比例。
所以答案是:×
【点睛】此题考查了学生对圆的周长和面积公式的应用。
18.√
【分析】依据比例的基本性质,即两个内项之积等于两个外项之积,即可进行判断。
【详解】在一个比例中,两个外项交换位置后,两个内项之积仍然等于两个外项之积,所以仍是比例。例如:2∶3=4∶6,6∶3=4∶2。
故答案为:√
【点睛】此题主要考查比例的基本性质,解答时可以举例证明。
19.×
【分析】抓住“0”这个特殊的数,a、b、c、d应有个取值范围,因为0不能做除数,所以原题说法错误。
【详解】在这个式子中,是用字母a、b、c、d来表示数的,因为除数不能为0,所以a、b、c、d应有个取值范围,也就是:它们应该都是非0的数才能成立,原题题干不严谨。
故答案为:×
【点睛】此题关键在于通过数学语言和结论的严谨性来判断,0不能做除数和分母。
20.;;
【分析】根据等式的性质解方程即可。
(1)先算得,等式两边再同时乘;
(2)根据比例的基本性质,把比例转化成方程,等式两边再同时乘;
(3)等式两边先同时加上4.2,再同时乘。
【详解】(1)
解:=35
x=30
(2)
解:
x=
(3)
解:
x=16.5
21.2400克
【分析】设要用水x克,妈妈用800克雪梨和2000克水制作雪梨汤,口感极好,即雪梨的克数和水的克数比不变;根据比例的意义,960克雪梨∶x克水的比值等于800克雪梨∶2000克水,列方程:960∶x=800∶2000,解比例,即可解答。
【详解】解:设她要用水x克
960∶x=800∶2000
800x=960×2000
800x=1920000
x=2400
答:她要用水2400克。
【点睛】本题考查比例的意义,根据比例的意义列比例,解比例,进行解答。
22.公鸡20只;母鸡80只
【分析】方法1:公鸡占母鸡只数的,相当于把100只鸡平均分成5份,公鸡占1份,母鸡占4份,用100×求出公鸡数量,用100×求出母鸡数量。
方法2:设公鸡数量为x只,母鸡数量为(100-x)只。用x∶(100-x)=,解答即可。
【详解】由分析可知:
方法1:公鸡数量:100×=20(只)
母鸡数量:100×(1-)
=100×
=80(只)
方法2:解:设公鸡数量为x只,母鸡数量为(100-x)只。
x∶(100-x)=
100-x=4x
5x=100
x=20
母鸡:100-20=80(只)
答:李奶奶养公鸡20只,母鸡80只。
【点睛】此题主要考查学生对比例的理解与应用。
23.150千米
【分析】根据比例尺=图上距离∶实际距离;实际距离=图上距离÷比例尺,代入数据,即可解答。
【详解】5÷
=5×3000000
=15000000(厘米)
15000000厘米=150(千米)
答:两地实际相距150千米。
【点睛】本题考查比例尺的应用,解答本题的关键是掌握比例尺中的数量关系式。
24.(1)(4,7);图见详解;
(2)见详解;
(3)东;北;60
【分析】(1)将三角形ABC绕点A逆时针旋转90°后,A点位置不变,C点旋转到(4,7),B点旋转到(0,7),连接旋转后的B点和A点即成三角形ABC绕点A逆时针旋转90°后的图形;
(2)原来的三角形ABC两条直角分别为2格和4格,按1∶2缩小后两条直角边分别为1格和2格,先画出两边直角边,再连接出斜边即可;
(3)以M为观测点,MN在正东方,三角形MNP是等边三角形,则∠PMN是60°,据此可判断P点的方向。
【详解】画图如下:
(1)三角形ABC绕点A逆时针旋转90°后的图形如上图,旋转后点C对应的位置用数对表示为(4,7);
(2)三角形ABC按1∶2的比缩小后的图形如上图;
(3)P点在M点的东偏北60°方向上。
【点睛】此题重点考查平面图形旋转和缩小的方法,以及以数对确定位置、以正方向加偏转角度确定方向的方法。
25.1.2小时
【分析】图上距离和比例尺已知,依据“图上距离÷比例尺=实际距离”即可求出两地的实际距离。再根据“时间=路程÷速度”即可求出。
【详解】5.9÷=17700000(厘米)
17700000厘米=177千米
177÷144≈1.2(小时)
答:列车行完全程需要1.2小时。
【点睛】此题主要考查图上距离、实际距离和比例尺之间的关系,以及行程问题中的基本数量关系“时间=路程÷速度”。
26.(1)1∶7000000;(2)2100千米
【分析】(1)图上距离∶实际距离=比例尺。据此先统一单位再解答。
(2)根据(1)题中求出的这幅地图的比例尺,得出图上1厘米的距离表示实际多少千米,再乘30即可解答。
【详解】(1)280千米=28000000厘米
4∶28000000=1∶7000000
答:这幅地图的比例尺是1∶7000000。
(2)7000000=70千米
70×30=2100(千米)
答:成都到北京的实际距离约是2100千米。
【点睛】本题考查比例尺的应用。根据比例尺的意义明确图上1厘米的距离表示实际多少千米是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
