应用题特训-圆柱与圆锥(专项突破)-小学数学六年级下册北师大版(含答案)
文档属性
| 名称 | 应用题特训-圆柱与圆锥(专项突破)-小学数学六年级下册北师大版(含答案) | 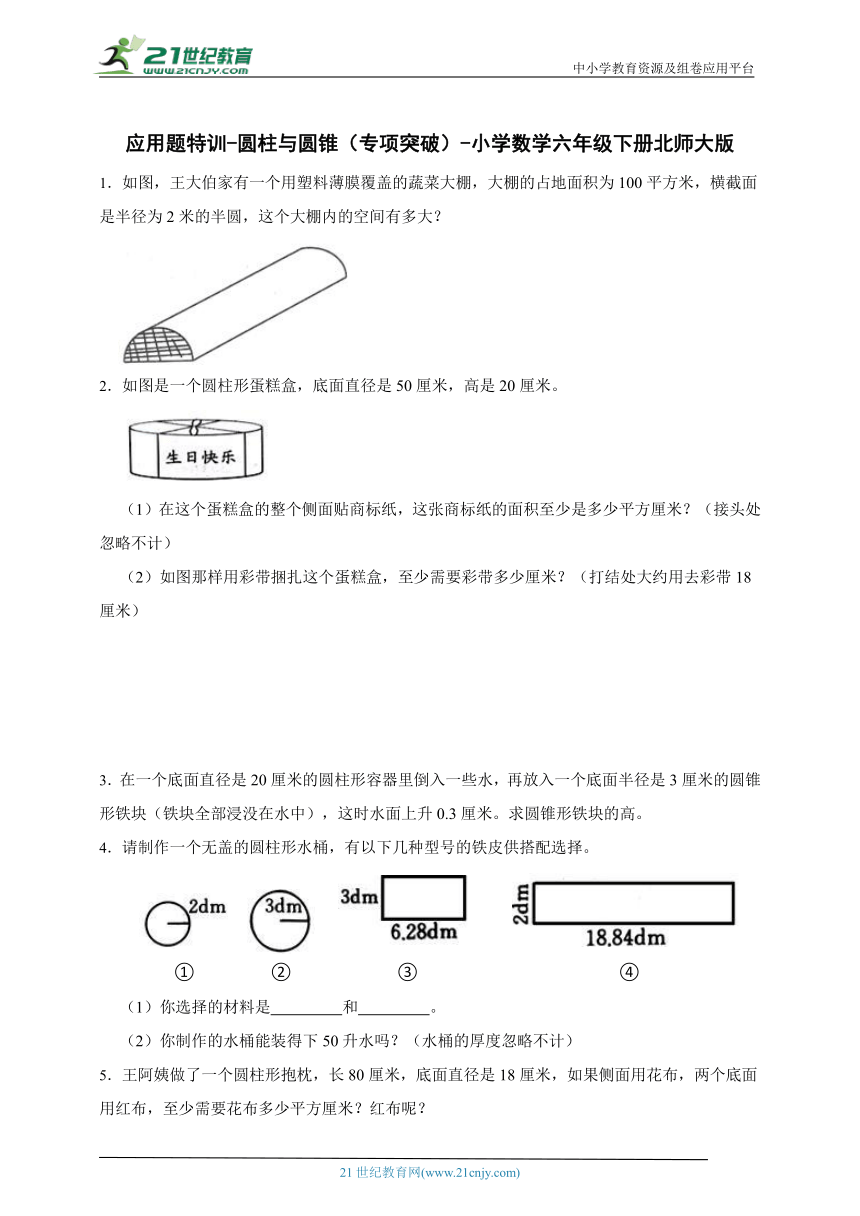 | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 12:43:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
应用题特训-圆柱与圆锥(专项突破)-小学数学六年级下册北师大版
1.如图,王大伯家有一个用塑料薄膜覆盖的蔬菜大棚,大棚的占地面积为100平方米,横截面是半径为2米的半圆,这个大棚内的空间有多大?
2.如图是一个圆柱形蛋糕盒,底面直径是50厘米,高是20厘米。
(1)在这个蛋糕盒的整个侧面贴商标纸,这张商标纸的面积至少是多少平方厘米?(接头处忽略不计)
(2)如图那样用彩带捆扎这个蛋糕盒,至少需要彩带多少厘米?(打结处大约用去彩带18厘米)
3.在一个底面直径是20厘米的圆柱形容器里倒入一些水,再放入一个底面半径是3厘米的圆锥形铁块(铁块全部浸没在水中),这时水面上升0.3厘米。求圆锥形铁块的高。
4.请制作一个无盖的圆柱形水桶,有以下几种型号的铁皮供搭配选择。
① ② ③ ④
(1)你选择的材料是 和 。
(2)你制作的水桶能装得下50升水吗?(水桶的厚度忽略不计)
5.王阿姨做了一个圆柱形抱枕,长80厘米,底面直径是18厘米,如果侧面用花布,两个底面用红布,至少需要花布多少平方厘米?红布呢?
6.下图是一个直径为10厘米的木制陀螺,陀螺圆柱部分的高是2厘米,圆锥部分的高是1.2厘米,这个陀螺的体积是多少立方厘米?
7.周师傅要把一个圆柱形木料(如下图)加工成圆锥形。
(1)圆锥的体积最大是多少立方分米?
(2)你还能提出什么问题?并列式解答。
8.一个高50厘米,底面半径4厘米的圆柱形容器,里面水深15厘米,把一个底面半径是2厘米的圆锥形铁块完全浸没在这个圆柱形水中,水面上升了6厘米。这个圆锥形铁块的体积是多少?
9.盾构机是一种使用盾构法的隧道挖掘机。如图所示,盾构机前端的盾构刀盘直径约为15米,相当于五层楼的高度。其基本工作原理是沿隧道轴线向前推进,通过旋转前端盾型结构,利用安装在前端的刀盘对土壤进行开挖切削,挖掘出来的土壤被输送到后方。该盾构机掘进10米,挖掘出来的土有多少立方米?
10.一个近似于圆锥形的沙堆,底面直径3.6米,高1.5米,
(1)这个沙堆的占地面积是多少平方米?
(2)这个沙堆所占的空间是多少立方米?
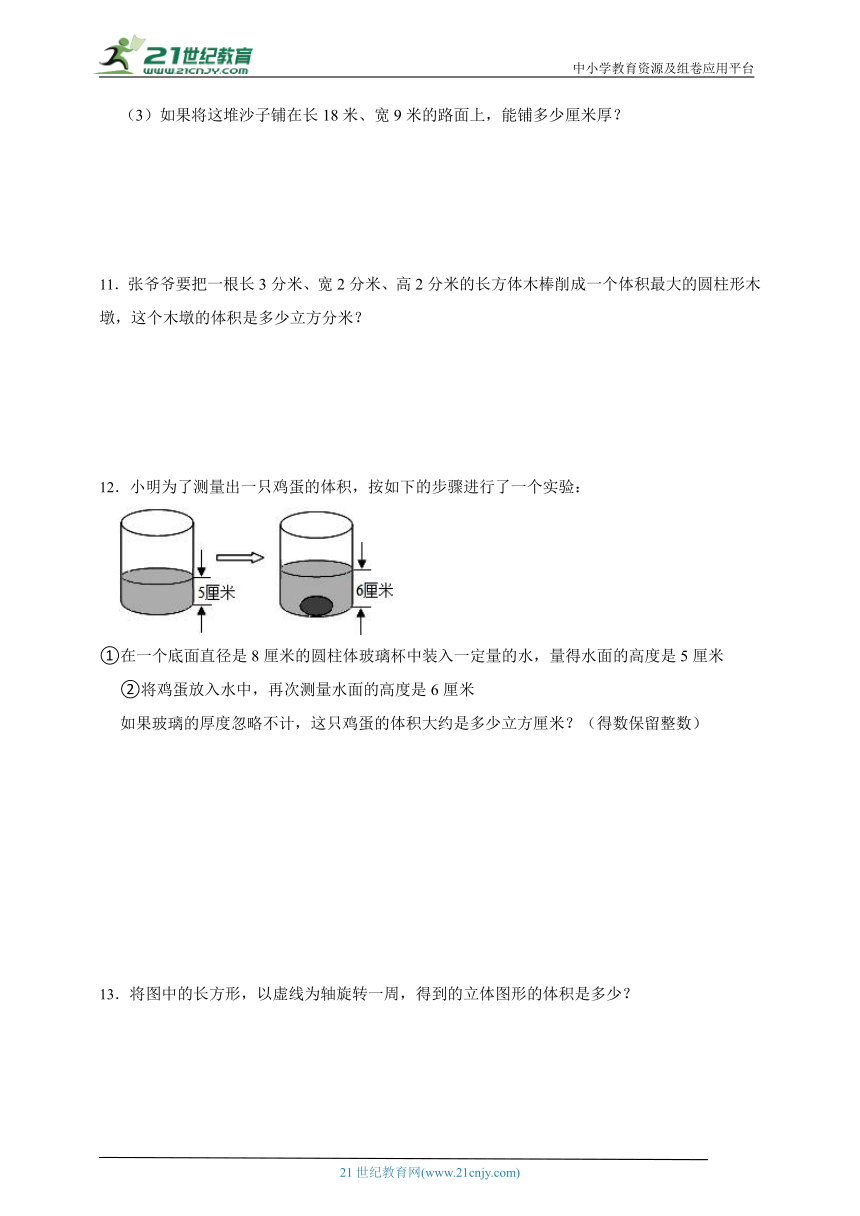
(3)如果将这堆沙子铺在长18米、宽9米的路面上,能铺多少厘米厚?
11.张爷爷要把一根长3分米、宽2分米、高2分米的长方体木棒削成一个体积最大的圆柱形木墩,这个木墩的体积是多少立方分米?
12.小明为了测量出一只鸡蛋的体积,按如下的步骤进行了一个实验:
①在一个底面直径是8厘米的圆柱体玻璃杯中装入一定量的水,量得水面的高度是5厘米
②将鸡蛋放入水中,再次测量水面的高度是6厘米
如果玻璃的厚度忽略不计,这只鸡蛋的体积大约是多少立方厘米?(得数保留整数)
13.将图中的长方形,以虚线为轴旋转一周,得到的立体图形的体积是多少?
14.一个圆柱体,高减少4厘米,表面积就减少50.24平方厘米,这个圆柱的底面积是多少平方厘米?(π取3.14)
15.张师傅用白铁皮做了一对圆柱形无盖水桶,底面直径是4dm,高是5dm。问:做这对水桶至少用去白铁皮多少平方分米?
16.下图的“博士帽”是用卡纸做成的,上面是边长30cm的正方形,下面是底面直径为18cm,高为8cm的无盖无底的圆柱。制作200顶这样的“博士帽”至少需要卡纸多少平方分米?
17.为实现全民健身,春天小区要建造一个圆柱形游泳池,底面直径30米,深2.5米。
(1)在游泳池的内壁和底面抹上水泥,抹水泥部分的面积是多少平方米?
(2)给这个游泳道注水,使水深是池深的 ,应注多少立方米的水?
18.有一段钢可做一个底面直径6厘米,高9厘米的圆锥体零件。如果把它改制成高是6厘米的圆柱体零件,零件的底面积是多少平方厘米?
答案解析部分
1.【答案】解:100÷(2×2)=25(米)
22×3.14×25÷2
=12.56×25÷2
=314÷2
=157(平方米)
答:这个大棚内的空间是157平方米。
2.【答案】(1)解:50×3.14×20
=157×20
=3140(平方厘米)
答:这张商标纸的面积至少是3140平方厘米。
(2)解:50×4+20×4+18
=200+80+18
=298(厘米)
答:至少需要彩带298厘米。
3.【答案】解:(20÷2)2×3.14×0.3
=314×0.3
=94.2(平方厘米)
94.2÷÷(32×3.14)
=282.6÷28.26
=10(厘米)
答:圆锥形铁块的高是10厘米。
4.【答案】(1)②;④
(2)解:3.14×32×2
=3.14×18
=56.52(立方分米)
56.52立方分米>50升
答:制作的水桶能装下50升水。
5.【答案】解:花布:3.14×18×80
=3.14×1440
=4521.6(平方厘米)
红布:3.14×(18÷2)2×2
=3.14×81×2
=508.68(平方厘米)
答:至少需要花布4521.6平方厘米,红布508.68平方厘米。
6.【答案】解:3.14×(10÷2)2×2+3.14×(10÷2)2×1.2×
=3.14×50+3.14×10
=3.14×60
=188.4(立方厘米)
答:这个陀螺的体积是188.4立方厘米。
7.【答案】(1)解:3.14×102×6×
=3.14×100×2
=628(立方分米)
答:圆锥的体积最大是628立方分米。
(2)解:这个圆柱形木料的表面积是多少平方分米?
3.14×102×2+3.14×10×2×6
=3.14×200+3.14×120
=628+376.8
=1004.8(平方厘米)
答:这个圆柱形木料的表面积是1004.8平方厘米
8.【答案】解:42×3.14×6
=50.24×6
=301.44(立方厘米)
答:这个圆锥形铁块的体积是301.44立方厘米。
9.【答案】解:(15÷2)2×3.14×10
=56.25×3.14×10
=176.625×10
=1766.25(立方米)
答:挖掘出来的土有1766.25立方米。
10.【答案】(1)解:(3.6÷2)2×3.14
=3.24×3.14
=10.1736(平方米)
答:这个沙堆的占地面积是10.1736平方米。
(2)解:10.1736×1.5×=5.0868(立方米)
答:这个沙堆所占的空间是5.0868立方米。
(3)解:5.0868÷18÷9
=0.2826÷9
=0.0314(米)
=3.14(厘米)
答:能铺3.14厘米厚。
11.【答案】解:(2÷2)2×3.14×3
=3.14×3
=9.42(立方分米)
答:这个木墩的体积是9.42立方分米。
12.【答案】解:底面积 S=πr2=3.14×(8÷2)2=50.24(平方厘米)
水的体积V=sh=50.24×5=251.2(立方厘米)
放入鸡蛋后水的体积 V=sh=50.24×6=301.44(立方厘米)
鸡蛋的体积=放入鸡蛋后水的体积-水的体积
=301.44-251.2
=50.24(立方厘米)
≈50(立方厘米)
答:这只鸡蛋的体积大约是50立方厘米。
13.【答案】解:3.14×32×4
=3.14×9×4
=113.04(立方厘米)
答:得到的是一个圆柱体,体积是113.04立方厘米。
14.【答案】解:圆柱的底面周长:50.24÷4=12.56(厘米)
圆柱的底面积是:3.14×(12.56÷3.14÷2)2
=3.14×22
=3.14×4
=12.56(平方厘米)
答:这根圆柱的底面积是12.56平方厘米。
15.【答案】解:4÷2=2(分米)
3.14×4×5+3.14×2×2
=62.8+12.56
=75.36(平方分米)
75.36×2=150.72(平方分米)
答:做这对水桶至少用去白铁皮150.72平方分米。
16.【答案】解:30×30=900(平方厘米)
3.14×18×8=56.52×8=452.16(平方厘米)
900+452.16=1352.16(平方厘米)=13.5216(平方分米)
13.5216×200=2704.32(平方分米)
答:制作200顶这样的“博士帽”至少需要卡纸2704.32平方分米。
17.【答案】(1)解:3.14×(30÷2)2+3.14×30×2.5
=3.14×225+3.14×75
=3.14×300
=942(平方米)
答:抹水泥部分的面积是942平方米。
(2)解:3.14×(30÷2)2×(2.5×)
=3.14×225×2
=3.14×450
=1413(立方米)
答:应注1413立方米的水。
18.【答案】解:3.14×(6÷2)2×9×÷6
=3.14×9×3÷6
=84.78÷6
=14.13(平方厘米)
答:零件的底面积是14.13平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
应用题特训-圆柱与圆锥(专项突破)-小学数学六年级下册北师大版
1.如图,王大伯家有一个用塑料薄膜覆盖的蔬菜大棚,大棚的占地面积为100平方米,横截面是半径为2米的半圆,这个大棚内的空间有多大?
2.如图是一个圆柱形蛋糕盒,底面直径是50厘米,高是20厘米。
(1)在这个蛋糕盒的整个侧面贴商标纸,这张商标纸的面积至少是多少平方厘米?(接头处忽略不计)
(2)如图那样用彩带捆扎这个蛋糕盒,至少需要彩带多少厘米?(打结处大约用去彩带18厘米)
3.在一个底面直径是20厘米的圆柱形容器里倒入一些水,再放入一个底面半径是3厘米的圆锥形铁块(铁块全部浸没在水中),这时水面上升0.3厘米。求圆锥形铁块的高。
4.请制作一个无盖的圆柱形水桶,有以下几种型号的铁皮供搭配选择。
① ② ③ ④
(1)你选择的材料是 和 。
(2)你制作的水桶能装得下50升水吗?(水桶的厚度忽略不计)
5.王阿姨做了一个圆柱形抱枕,长80厘米,底面直径是18厘米,如果侧面用花布,两个底面用红布,至少需要花布多少平方厘米?红布呢?
6.下图是一个直径为10厘米的木制陀螺,陀螺圆柱部分的高是2厘米,圆锥部分的高是1.2厘米,这个陀螺的体积是多少立方厘米?
7.周师傅要把一个圆柱形木料(如下图)加工成圆锥形。
(1)圆锥的体积最大是多少立方分米?
(2)你还能提出什么问题?并列式解答。
8.一个高50厘米,底面半径4厘米的圆柱形容器,里面水深15厘米,把一个底面半径是2厘米的圆锥形铁块完全浸没在这个圆柱形水中,水面上升了6厘米。这个圆锥形铁块的体积是多少?
9.盾构机是一种使用盾构法的隧道挖掘机。如图所示,盾构机前端的盾构刀盘直径约为15米,相当于五层楼的高度。其基本工作原理是沿隧道轴线向前推进,通过旋转前端盾型结构,利用安装在前端的刀盘对土壤进行开挖切削,挖掘出来的土壤被输送到后方。该盾构机掘进10米,挖掘出来的土有多少立方米?
10.一个近似于圆锥形的沙堆,底面直径3.6米,高1.5米,
(1)这个沙堆的占地面积是多少平方米?
(2)这个沙堆所占的空间是多少立方米?
(3)如果将这堆沙子铺在长18米、宽9米的路面上,能铺多少厘米厚?
11.张爷爷要把一根长3分米、宽2分米、高2分米的长方体木棒削成一个体积最大的圆柱形木墩,这个木墩的体积是多少立方分米?
12.小明为了测量出一只鸡蛋的体积,按如下的步骤进行了一个实验:
①在一个底面直径是8厘米的圆柱体玻璃杯中装入一定量的水,量得水面的高度是5厘米
②将鸡蛋放入水中,再次测量水面的高度是6厘米
如果玻璃的厚度忽略不计,这只鸡蛋的体积大约是多少立方厘米?(得数保留整数)
13.将图中的长方形,以虚线为轴旋转一周,得到的立体图形的体积是多少?
14.一个圆柱体,高减少4厘米,表面积就减少50.24平方厘米,这个圆柱的底面积是多少平方厘米?(π取3.14)
15.张师傅用白铁皮做了一对圆柱形无盖水桶,底面直径是4dm,高是5dm。问:做这对水桶至少用去白铁皮多少平方分米?
16.下图的“博士帽”是用卡纸做成的,上面是边长30cm的正方形,下面是底面直径为18cm,高为8cm的无盖无底的圆柱。制作200顶这样的“博士帽”至少需要卡纸多少平方分米?
17.为实现全民健身,春天小区要建造一个圆柱形游泳池,底面直径30米,深2.5米。
(1)在游泳池的内壁和底面抹上水泥,抹水泥部分的面积是多少平方米?
(2)给这个游泳道注水,使水深是池深的 ,应注多少立方米的水?
18.有一段钢可做一个底面直径6厘米,高9厘米的圆锥体零件。如果把它改制成高是6厘米的圆柱体零件,零件的底面积是多少平方厘米?
答案解析部分
1.【答案】解:100÷(2×2)=25(米)
22×3.14×25÷2
=12.56×25÷2
=314÷2
=157(平方米)
答:这个大棚内的空间是157平方米。
2.【答案】(1)解:50×3.14×20
=157×20
=3140(平方厘米)
答:这张商标纸的面积至少是3140平方厘米。
(2)解:50×4+20×4+18
=200+80+18
=298(厘米)
答:至少需要彩带298厘米。
3.【答案】解:(20÷2)2×3.14×0.3
=314×0.3
=94.2(平方厘米)
94.2÷÷(32×3.14)
=282.6÷28.26
=10(厘米)
答:圆锥形铁块的高是10厘米。
4.【答案】(1)②;④
(2)解:3.14×32×2
=3.14×18
=56.52(立方分米)
56.52立方分米>50升
答:制作的水桶能装下50升水。
5.【答案】解:花布:3.14×18×80
=3.14×1440
=4521.6(平方厘米)
红布:3.14×(18÷2)2×2
=3.14×81×2
=508.68(平方厘米)
答:至少需要花布4521.6平方厘米,红布508.68平方厘米。
6.【答案】解:3.14×(10÷2)2×2+3.14×(10÷2)2×1.2×
=3.14×50+3.14×10
=3.14×60
=188.4(立方厘米)
答:这个陀螺的体积是188.4立方厘米。
7.【答案】(1)解:3.14×102×6×
=3.14×100×2
=628(立方分米)
答:圆锥的体积最大是628立方分米。
(2)解:这个圆柱形木料的表面积是多少平方分米?
3.14×102×2+3.14×10×2×6
=3.14×200+3.14×120
=628+376.8
=1004.8(平方厘米)
答:这个圆柱形木料的表面积是1004.8平方厘米
8.【答案】解:42×3.14×6
=50.24×6
=301.44(立方厘米)
答:这个圆锥形铁块的体积是301.44立方厘米。
9.【答案】解:(15÷2)2×3.14×10
=56.25×3.14×10
=176.625×10
=1766.25(立方米)
答:挖掘出来的土有1766.25立方米。
10.【答案】(1)解:(3.6÷2)2×3.14
=3.24×3.14
=10.1736(平方米)
答:这个沙堆的占地面积是10.1736平方米。
(2)解:10.1736×1.5×=5.0868(立方米)
答:这个沙堆所占的空间是5.0868立方米。
(3)解:5.0868÷18÷9
=0.2826÷9
=0.0314(米)
=3.14(厘米)
答:能铺3.14厘米厚。
11.【答案】解:(2÷2)2×3.14×3
=3.14×3
=9.42(立方分米)
答:这个木墩的体积是9.42立方分米。
12.【答案】解:底面积 S=πr2=3.14×(8÷2)2=50.24(平方厘米)
水的体积V=sh=50.24×5=251.2(立方厘米)
放入鸡蛋后水的体积 V=sh=50.24×6=301.44(立方厘米)
鸡蛋的体积=放入鸡蛋后水的体积-水的体积
=301.44-251.2
=50.24(立方厘米)
≈50(立方厘米)
答:这只鸡蛋的体积大约是50立方厘米。
13.【答案】解:3.14×32×4
=3.14×9×4
=113.04(立方厘米)
答:得到的是一个圆柱体,体积是113.04立方厘米。
14.【答案】解:圆柱的底面周长:50.24÷4=12.56(厘米)
圆柱的底面积是:3.14×(12.56÷3.14÷2)2
=3.14×22
=3.14×4
=12.56(平方厘米)
答:这根圆柱的底面积是12.56平方厘米。
15.【答案】解:4÷2=2(分米)
3.14×4×5+3.14×2×2
=62.8+12.56
=75.36(平方分米)
75.36×2=150.72(平方分米)
答:做这对水桶至少用去白铁皮150.72平方分米。
16.【答案】解:30×30=900(平方厘米)
3.14×18×8=56.52×8=452.16(平方厘米)
900+452.16=1352.16(平方厘米)=13.5216(平方分米)
13.5216×200=2704.32(平方分米)
答:制作200顶这样的“博士帽”至少需要卡纸2704.32平方分米。
17.【答案】(1)解:3.14×(30÷2)2+3.14×30×2.5
=3.14×225+3.14×75
=3.14×300
=942(平方米)
答:抹水泥部分的面积是942平方米。
(2)解:3.14×(30÷2)2×(2.5×)
=3.14×225×2
=3.14×450
=1413(立方米)
答:应注1413立方米的水。
18.【答案】解:3.14×(6÷2)2×9×÷6
=3.14×9×3÷6
=84.78÷6
=14.13(平方厘米)
答:零件的底面积是14.13平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
