2022——2023学年人教版数学八年级下册 19.1.2函数的图像(第二课时)课件(共25张PPT)
文档属性
| 名称 | 2022——2023学年人教版数学八年级下册 19.1.2函数的图像(第二课时)课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 362.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 07:20:07 | ||
图片预览




文档简介
(共25张PPT)
19.1.2 函数的图象
第二课时
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象。
对于一些函数,我们通过列表、描点、连线画出它们的图象。
函数的图象:
复习回顾:
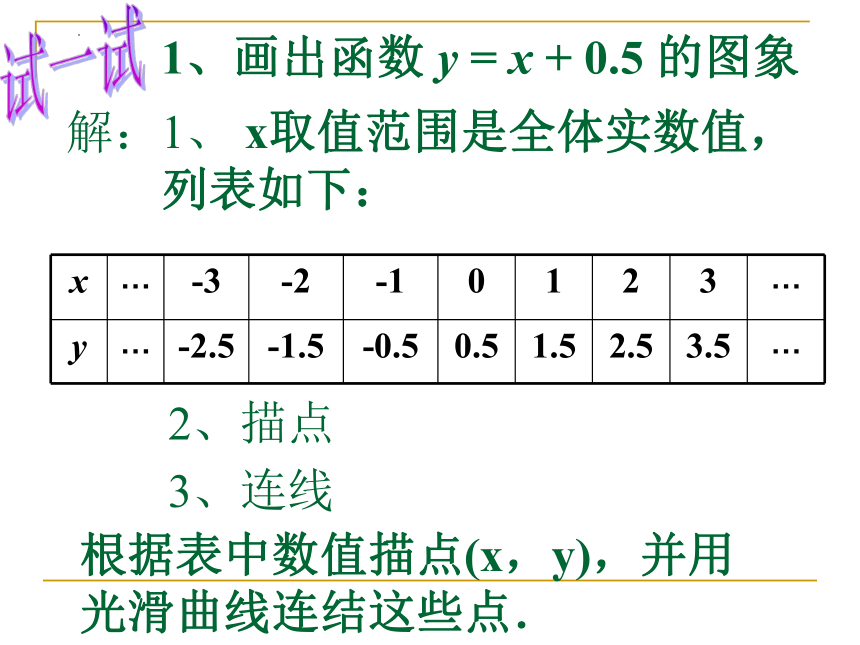
1、画出函数 y = x + 0.5 的图象
1、 x取值范围是全体实数值,
列表如下:
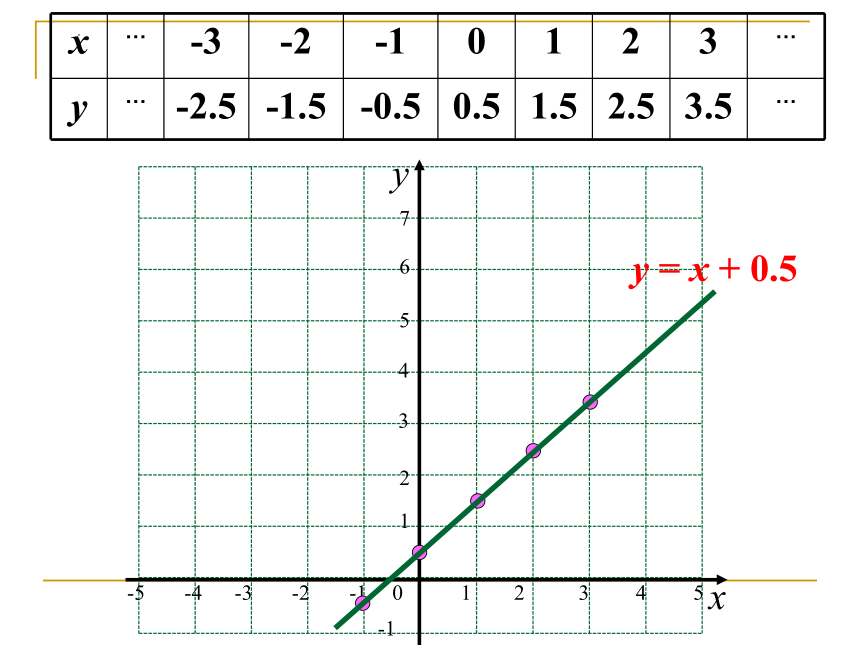
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
解:
2、描点
3、连线
试一试
根据表中数值描点(x,y),并用光滑曲线连结这些点.
x
y
0
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
y = x + 0.5
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
3、连线
函数图象的画法:
1、列表
2、描点
列出自变量与函数的对应值表(注意自变量的 取值范围,一般取7个点)
根据自变量与函数的对应值描点(表示与之对应的点有无数个,但实际上我们只能描出其中有限个点,同时想象出其他点的位置.)
按照横坐标由小到大顺序用平滑曲线依次连接各点
归纳
1、画出函数 的图象。
练习
2、画出函数 的图象。
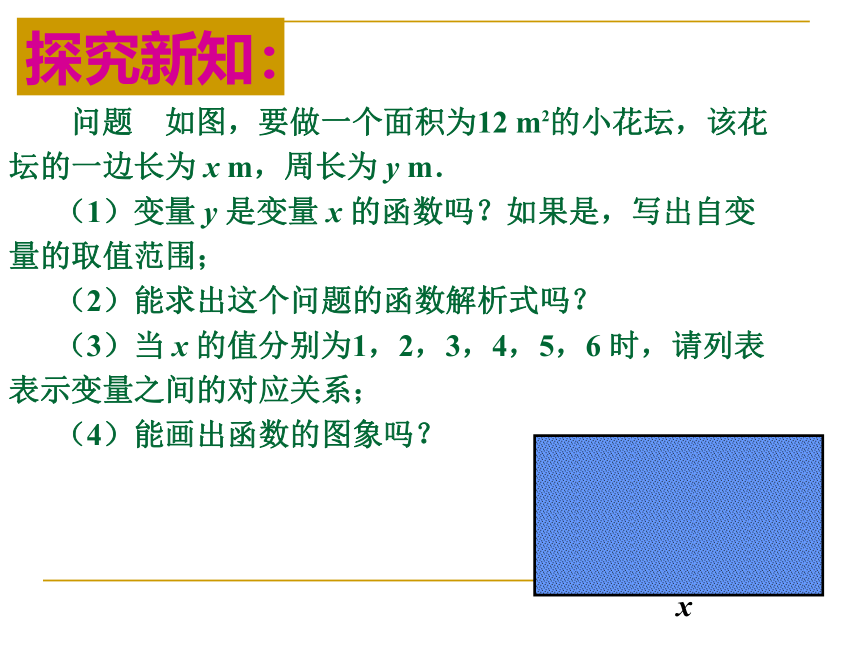
问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变
量的取值范围;
(2)能求出这个问题的函数解析式吗?
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表
表示变量之间的对应关系;
(4)能画出函数的图象吗?
x
探究新知:
x
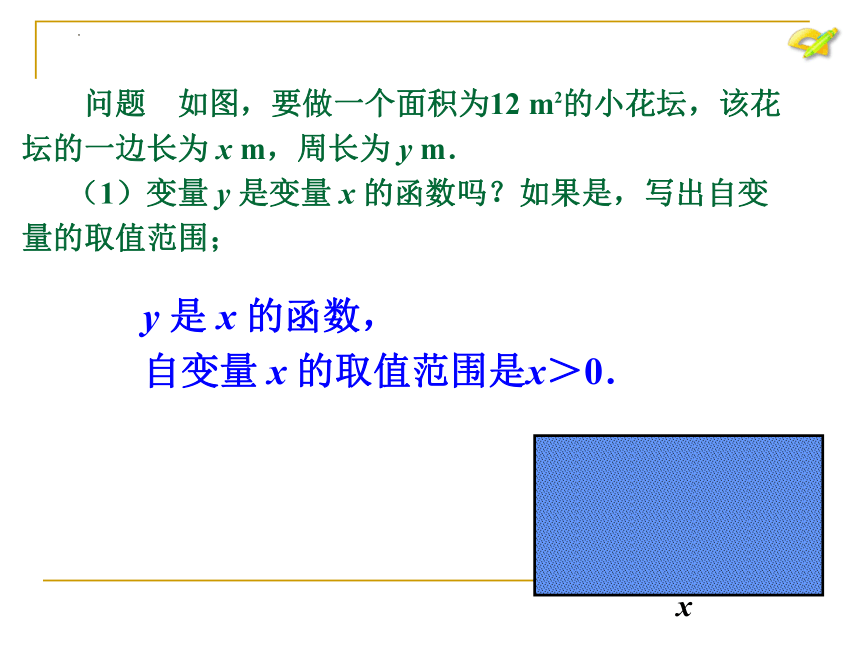
y 是 x 的函数,
自变量 x 的取值范围是x>0.
问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变
量的取值范围;
x
y =2(x + )
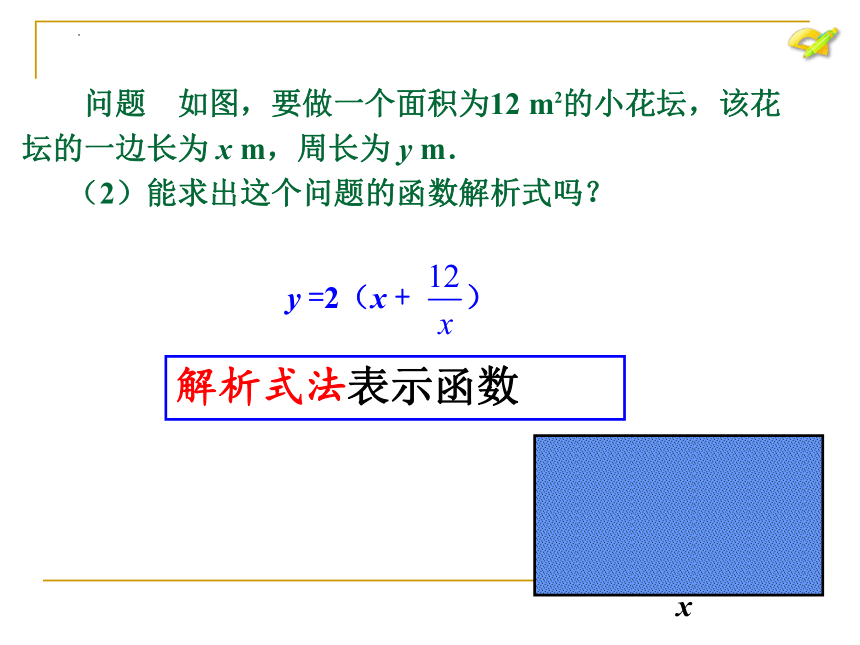
问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(2)能求出这个问题的函数解析式吗?
解析式法表示函数
x
x/m 1 2 3 4 5 6
y/m 26 16 14 14 14.8 16
问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表
表示变量之间的对应关系;
列表法表示函数
x/m 1 2 3 4 5 6
y/m 26 16 14 14 14.8 16
问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(4)能画出函数的图象吗?
40
35
30
25
20
15
10
5
5
10
O
x
y
图象法表示函数
合作探究:
说说函数的三种表示方法各有什么优点和不足,分
小组讨论一下.
思考
(1)对于每一个大于0 的自变量的值,想准确确定
对应的函数值,用什么表示法较好?
(2)对于x 的值分别为1,2,3,4,5,6 时,想知
道其对应的函数值,用什么表示方法较好?
(3)想知道当x 的值增大时,函数值y 怎样变化,用
什么表示方法较好?
表示函数关系的方法:
1、解析式法:
全面、准确地给出自变量和函数的数量关系;
2、列表法:
准确、直观地给出部分自变量与函数的对应值;
3、图象法:
直观、形象地表示自变量与函数值的变化趋势.
归纳
表示方法
全面性
准确性
直观性
形象性
列表法
解析式法
图象法
例题讲解
例:一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度
t/时 0 1 2 3 4 5
y/米 10 10.05 10.10 10.15 10.20 10.25
1.由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数图象.
O
5
10
10.25
t
y
解:1、y=0.05t+10(0≤t≤5)
例:一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度
t/时 0 1 2 3 4 5
y/米 10 10.05 10.10 10.15 10.20 10.25
2.据估计这种上涨的情况还会持续2小时,预测再过2小时水位高度将达到多少米?
由1知y与t的函数解析式为: y=0.05t+10(0≤t≤5)
解:再过2小时的水位高度,就是t=5+2=7时,y=0.05t+10的函数值,从解析式容易算出:y=0.05×7+10=10.35
答:2小时后,预计水位高10.35米.
把函数的图像向右延伸到t=7所对应的位置,也可以估计出这个值
就上面的例子请大家思考:函数的三种表示方法之间是否可以转化?
从这个例子可以看出函数的三种不同表示法可以转化,因为题目中只给出了列表法,而我们通过分析求出解析式并画出了图象,所以可以相互转化.
1、一个水管以固定的速度向容积为100 m3的水池中注水,注水时间t与水池的水量Q 如下表所示:
(1)请从表中找出t与Q之间的函数关系式,并画出函数的图象;
(2)求当t=15 min时,水池中的水量Q的值.
t(min) 0 2 4 6 8 …
Q(m3) 20 24 28 32 36 …
巩固练习
思考:当我们无法直接得到某一运动变化过程的函数
解析式时,我们可以通过哪些步骤的研究,得
到函数解析式?
解: (1)由表中观察到开始时已有20 m3水量库存,以后每隔1分钟,水量增加2 m3.这样的变化规律可以表示为Q=2t+20(0≤t≤40),图象如答图所示.
(2)经过15 min后的水量,就是当t=15时,Q=2t+20的函数值,从解析式知Q=2×15+20=50;从函数图象也能估出这个值,如答图中A点的纵坐标,所以当t=15 min时,水池中的水量为50 m3.
2.已知某一函数的图象如图所示,根据图象回答下列问题:
(1)确定自变量的取值范围;
解:自变量的取值范围是-4≤X≤4;
(2)求当x=-4,-2,4时y的值是多少?
解:y的值分别是2, -2,0
(3)求当y=0,4时x的值是多少?
解:当y=0时,x的值是-3,-1或4
当y=4时,x=1.5
(4)当x取何值时y的值最大?当x取 何值时y的值最小?
解:当x=1.5时,y的值最大,值为4,
当x=-2时,y的值最小,值为-2。
(5)当x的值在什么范围内时y随x的增大而增大?
当x的值在什么范围内时y随x的增大而减小?
解:当-2 ≤x≤1.5时,y随x的增大而增大;
当-4≤x≤-2或1.5≤x≤4时,y随x的增大而减小。
巩固与检测
解:(1)从图象中观察得知:自变量
X的取值范围是:0≤x≤5
(2)从图象中观察得知:
当 x = 3 时,y 有最小值,最小值 y = 2.5
(3)从图象中观察得知:
y 随着 x 的增大而减小。
巩固与检测
3、
想一想
1、判断点(2,4)是否在函数y=2x图象上.
解:把x=2代入解析式,y=2×2=4.
所以,点(2,4)在函数y=2x图象上.
如何判定点是否在函数图象上?
把点的坐标代入函数解析式,如果满足解析式,这个点就在函数图象上,如果不满足解析式,这个点就不在函数图象上。
2、已知函数y=2x-3,求函数图象与x轴、y轴的交点坐标;
解:当y=0时,x=1.5,所以函数图象与x轴的交点坐标为(1.5,0).
当x=0时,y=-3,所以函数图象与y轴的交点坐标为(0,-3).
如何求函数图象与x轴、y轴的交点坐标?
求函数图象与x轴的交点就是令y=0,求函数与y轴的交点就是令x=0.
想一想
3、求函数y=-x与y=2x-1的图象的交点坐标。
如何求两个函数图象的交点坐标?
求两个函数图象的交点就是求这两个函数解析式所组成的方程组的解.
想一想
课堂小结
谈谈本节课的收获和疑惑
19.1.2 函数的图象
第二课时
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象。
对于一些函数,我们通过列表、描点、连线画出它们的图象。
函数的图象:
复习回顾:
1、画出函数 y = x + 0.5 的图象
1、 x取值范围是全体实数值,
列表如下:
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
解:
2、描点
3、连线
试一试
根据表中数值描点(x,y),并用光滑曲线连结这些点.
x
y
0
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
y = x + 0.5
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
3、连线
函数图象的画法:
1、列表
2、描点
列出自变量与函数的对应值表(注意自变量的 取值范围,一般取7个点)
根据自变量与函数的对应值描点(表示与之对应的点有无数个,但实际上我们只能描出其中有限个点,同时想象出其他点的位置.)
按照横坐标由小到大顺序用平滑曲线依次连接各点
归纳
1、画出函数 的图象。
练习
2、画出函数 的图象。
问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变
量的取值范围;
(2)能求出这个问题的函数解析式吗?
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表
表示变量之间的对应关系;
(4)能画出函数的图象吗?
x
探究新知:
x
y 是 x 的函数,
自变量 x 的取值范围是x>0.
问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变
量的取值范围;
x
y =2(x + )
问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(2)能求出这个问题的函数解析式吗?
解析式法表示函数
x
x/m 1 2 3 4 5 6
y/m 26 16 14 14 14.8 16
问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表
表示变量之间的对应关系;
列表法表示函数
x/m 1 2 3 4 5 6
y/m 26 16 14 14 14.8 16
问题 如图,要做一个面积为12 m2的小花坛,该花
坛的一边长为 x m,周长为 y m.
(4)能画出函数的图象吗?
40
35
30
25
20
15
10
5
5
10
O
x
y
图象法表示函数
合作探究:
说说函数的三种表示方法各有什么优点和不足,分
小组讨论一下.
思考
(1)对于每一个大于0 的自变量的值,想准确确定
对应的函数值,用什么表示法较好?
(2)对于x 的值分别为1,2,3,4,5,6 时,想知
道其对应的函数值,用什么表示方法较好?
(3)想知道当x 的值增大时,函数值y 怎样变化,用
什么表示方法较好?
表示函数关系的方法:
1、解析式法:
全面、准确地给出自变量和函数的数量关系;
2、列表法:
准确、直观地给出部分自变量与函数的对应值;
3、图象法:
直观、形象地表示自变量与函数值的变化趋势.
归纳
表示方法
全面性
准确性
直观性
形象性
列表法
解析式法
图象法
例题讲解
例:一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度
t/时 0 1 2 3 4 5
y/米 10 10.05 10.10 10.15 10.20 10.25
1.由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数图象.
O
5
10
10.25
t
y
解:1、y=0.05t+10(0≤t≤5)
例:一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度
t/时 0 1 2 3 4 5
y/米 10 10.05 10.10 10.15 10.20 10.25
2.据估计这种上涨的情况还会持续2小时,预测再过2小时水位高度将达到多少米?
由1知y与t的函数解析式为: y=0.05t+10(0≤t≤5)
解:再过2小时的水位高度,就是t=5+2=7时,y=0.05t+10的函数值,从解析式容易算出:y=0.05×7+10=10.35
答:2小时后,预计水位高10.35米.
把函数的图像向右延伸到t=7所对应的位置,也可以估计出这个值
就上面的例子请大家思考:函数的三种表示方法之间是否可以转化?
从这个例子可以看出函数的三种不同表示法可以转化,因为题目中只给出了列表法,而我们通过分析求出解析式并画出了图象,所以可以相互转化.
1、一个水管以固定的速度向容积为100 m3的水池中注水,注水时间t与水池的水量Q 如下表所示:
(1)请从表中找出t与Q之间的函数关系式,并画出函数的图象;
(2)求当t=15 min时,水池中的水量Q的值.
t(min) 0 2 4 6 8 …
Q(m3) 20 24 28 32 36 …
巩固练习
思考:当我们无法直接得到某一运动变化过程的函数
解析式时,我们可以通过哪些步骤的研究,得
到函数解析式?
解: (1)由表中观察到开始时已有20 m3水量库存,以后每隔1分钟,水量增加2 m3.这样的变化规律可以表示为Q=2t+20(0≤t≤40),图象如答图所示.
(2)经过15 min后的水量,就是当t=15时,Q=2t+20的函数值,从解析式知Q=2×15+20=50;从函数图象也能估出这个值,如答图中A点的纵坐标,所以当t=15 min时,水池中的水量为50 m3.
2.已知某一函数的图象如图所示,根据图象回答下列问题:
(1)确定自变量的取值范围;
解:自变量的取值范围是-4≤X≤4;
(2)求当x=-4,-2,4时y的值是多少?
解:y的值分别是2, -2,0
(3)求当y=0,4时x的值是多少?
解:当y=0时,x的值是-3,-1或4
当y=4时,x=1.5
(4)当x取何值时y的值最大?当x取 何值时y的值最小?
解:当x=1.5时,y的值最大,值为4,
当x=-2时,y的值最小,值为-2。
(5)当x的值在什么范围内时y随x的增大而增大?
当x的值在什么范围内时y随x的增大而减小?
解:当-2 ≤x≤1.5时,y随x的增大而增大;
当-4≤x≤-2或1.5≤x≤4时,y随x的增大而减小。
巩固与检测
解:(1)从图象中观察得知:自变量
X的取值范围是:0≤x≤5
(2)从图象中观察得知:
当 x = 3 时,y 有最小值,最小值 y = 2.5
(3)从图象中观察得知:
y 随着 x 的增大而减小。
巩固与检测
3、
想一想
1、判断点(2,4)是否在函数y=2x图象上.
解:把x=2代入解析式,y=2×2=4.
所以,点(2,4)在函数y=2x图象上.
如何判定点是否在函数图象上?
把点的坐标代入函数解析式,如果满足解析式,这个点就在函数图象上,如果不满足解析式,这个点就不在函数图象上。
2、已知函数y=2x-3,求函数图象与x轴、y轴的交点坐标;
解:当y=0时,x=1.5,所以函数图象与x轴的交点坐标为(1.5,0).
当x=0时,y=-3,所以函数图象与y轴的交点坐标为(0,-3).
如何求函数图象与x轴、y轴的交点坐标?
求函数图象与x轴的交点就是令y=0,求函数与y轴的交点就是令x=0.
想一想
3、求函数y=-x与y=2x-1的图象的交点坐标。
如何求两个函数图象的交点坐标?
求两个函数图象的交点就是求这两个函数解析式所组成的方程组的解.
想一想
课堂小结
谈谈本节课的收获和疑惑
