三角形复习课[下学期]

课件25张PPT。三角形的复习教学目标：
1：掌握三角形的基本要素及基本性质、全等。
2：灵活运用三角形的基本性质和全等条件。
重点：
掌握三角形全等的条件。

难点：
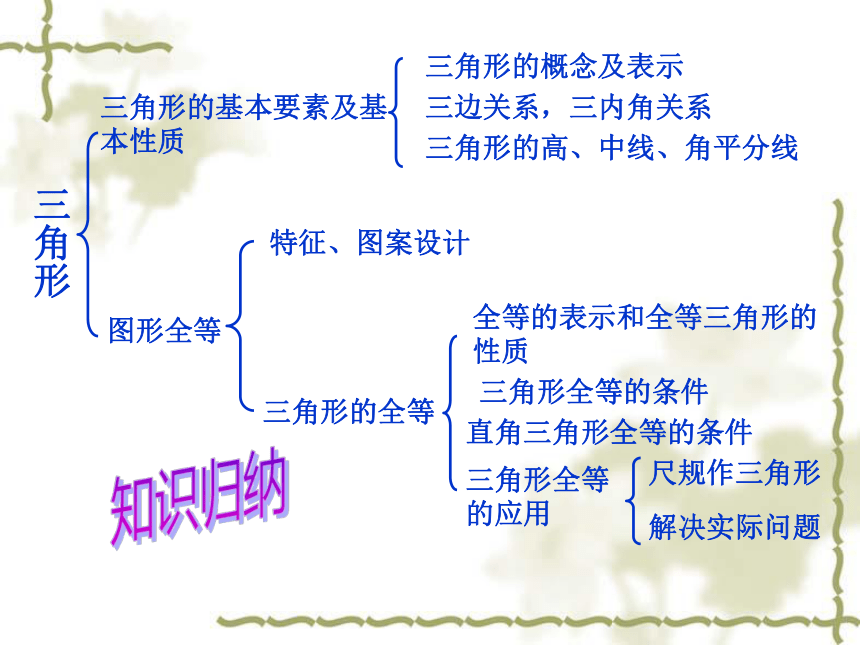
在直观认识和操作活动的基础上，运用自己的语言表达，发展推理能力。三角形的基本要素及基本性质三角形的概念及表示三边关系，三内角关系三角形的高、中线、角平分线图形全等特征、图案设计三角形的全等全等的表示和全等三角形的性质三角形全等的条件直角三角形全等的条件三角形三角形全等的应用尺规作三角形解决实际问题知识归纳知识要点总结1、三角形的边角关系(1)任意两边之和大于第三边，任意两边之差小于第三边（2）三角形的内角和等于1802、三角形分类三角形按角分为锐角三角形
直角三角形
钝角三角形3、三角形全等的条件（1）一般三角形：SAS、ASA、AAS、SSS（2）直角三角形：SAS、ASA、AAS、SSS、HL（3）全等三角形的性质①全等三角形对应角相等。
②全等三角形对应边相等。
③全等三角形周长相等，面积相等。4、尺规作图：只允许用直尺和圆规作三角形5、方法小结（1）分解图形法
复杂图形都是由较简单的基本图形组成，故可将复杂图形分解成基本图形。（2）构造图形法
当直接证题有困难时，常添加辅助线构造图形达到解题目的。解题方法指导一、证明线段相等的方法
1、中点定义
2、全等三角形对应边相等
3、等式性质二、证明角相等的方法
1、对顶角相等
2、同角（或等角）的余角相等
3、同角（或等角）的补角相等
4、两直线平行，同位角相等，内错角相等
5、全等三角形的对应角相等
6、等式性质
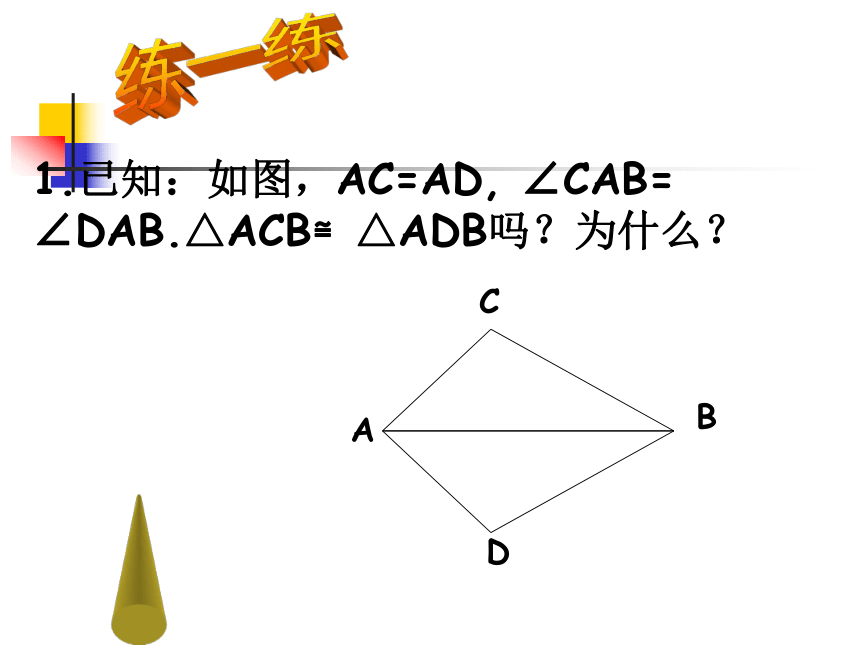
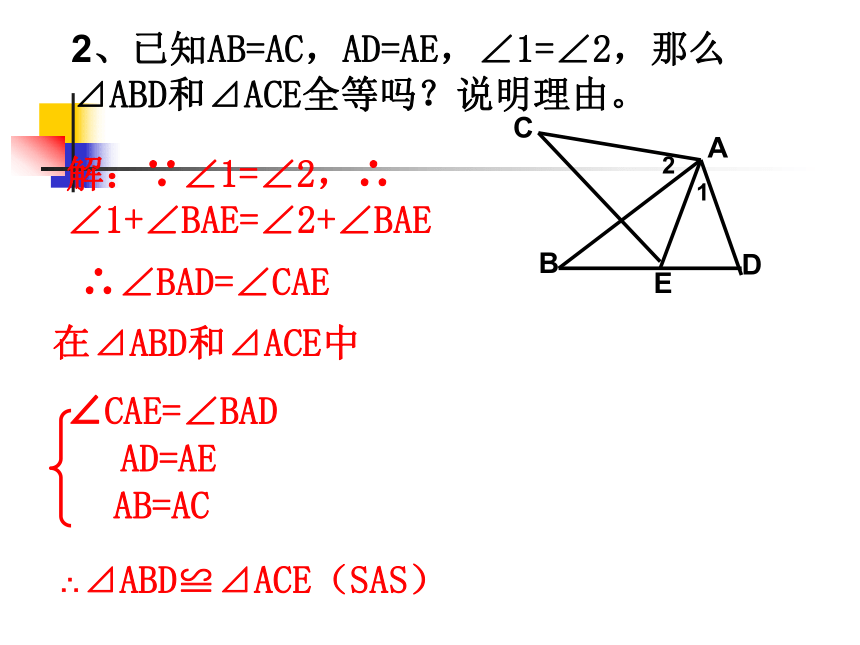
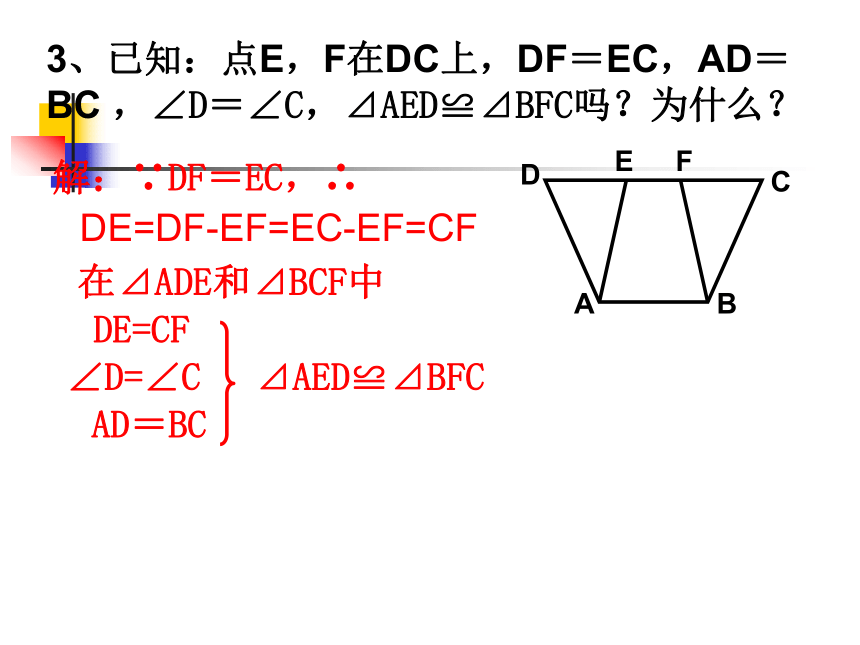
1.已知：如图，AC=AD, ∠CAB= ∠DAB.△ACB≌△ADB吗？为什么？练一练2、已知AB=AC，AD=AE，∠1=∠2，那么⊿ABD和⊿ACE全等吗？说明理由。ABDEC12解：∵∠1=∠2，∴ ∠1+∠BAE=∠2+∠BAE ∠CAE=∠BADAD=AEAB=AC∴⊿ABD≌⊿ACE（SAS）∴∠BAD=∠CAE在⊿ABD和⊿ACE中3、已知：点E，F在DC上，DF＝EC，AD＝BC ，∠D＝∠C，⊿AED≌⊿BFC吗？为什么？ABCDEF解：∵DF＝EC，∴DE=DF-EF=EC-EF=CF在⊿ADE和⊿BCF中DE=CF∠D=∠CAD＝BC⊿AED≌⊿BFC4、已知：AD⊥BC，D为垂足，AD=BD，DC＝DE，那么，∠C=∠BED。为什么？ABCDE分析：要∠C＝∠BED，只需证⊿ADC≌⊿BDE结合已知考虑“SAS”证之证明：∵AD⊥BC于D，∴∠ADC＝∠BDE＝90°在⊿ADC和⊿BDE 中AD＝BD∠ADC＝∠BDEDC＝DE⊿ADC≌⊿BDE∠C＝∠BED7.已知，如图：点E、F在BC上，BE=CF,AB=DC, ∠B=∠C.问：△ABF≌△DCE吗？为什么？8.已知，如图：点E、F在BC上，BE=CF,AB=DC, ∠B=∠C.求证：AF=DE检测三、机动练习 求：∠DBE的度数.
?
?
?
1 如图，A、B、C三点在一条直线上，DA⊥AC，EC⊥AC，DA⊥AC， AB=CE，AD=CB.
A
EC
B
D
?
?
2 如图，A、B、C三点在一条直线上，AD=AE，AC平分∠DAE，图中有多少对全等三角形？证明你的结论.
公园里有一条“Z”字型道路ABCD，如图，其中AB//CD。在AB、BC、CD三段路旁各有一小石凳E、F、M，M恰好为BC中点，且E、F、M在同一直线上，在BE道路中停放一排小汽车，从而无法直接测量B、E之间的距离。你能想出解决的方法吗？请说明其中的道理。ABCDEMF思路：只须证⊿BEM≌⊿CFM，求出CF的距离即知B、E间的距离某铁路施工队要打通一座小山建隧道，如图，设计时要测隧道的长度，恰好山前是一片空地，利用这样有利地形，测量人员是否可以利用三角形全等的知识测量出隧道长度，画出你设计的测量方法图，并说明理由。ABCDE我军在前进途中被大河挡住去路如图，当时部队没有任何测量工具，一战士仅用头上戴的军帽和一条绳子测得了河宽，使部队顺利架起浮桥。（1）这名战士如何测得河宽？
（2）你有不同方法吗？A B CD思考题：如图是某城市部分街道示意图，AB=BC= AC，CD= CE=DE，A、 B、C、D、E、F 、G、H为“中巴”停靠点，“中巴甲”从A站出发，按照A→H→G→D→E→C→F的顺序到达F站，“中巴乙”从B站出发，沿F→H→E→D→C→G 的顺序到达G站，若甲、乙分别从A、B站出发，在各站停的时间、车速均一样，试问哪一辆先到达指定站，为什么？ACDBEFHG 思路：看图可知：⊿ACD≌⊿BEC，∴AD=BE，ED=DE=EC=DC，
又⊿AGC≌⊿BFC，∴GC=FC，∴他们是同时到达。甲乙 注意利用全等三角形解决实际问题的步骤：
（1）先明确实际问题应用哪些几何知识解决。
（2）根据实际抽象出几何图形。
（3）结合图形和题意分析已知条件。
（4）找到解决问题的途径并表达清楚。在⊿ABC中，∠B=30°，BC边上的高h=4cm,AC=7cm分析：假设求作的三角形如图示BCAD30°4cm7cm60°4cm7cm60°已知：∠α，∠β，线段a为一角的对边，求作⊿ABC，使∠A=∠α，∠B=∠β，BC=a分析：假设求作的三角形如图示ABCαβ180°-α-βaαβ180°-α-βa小结：1、证角相等常用的方法：①对顶角相等。②同角（或等角）的余角相等（或补角相等）③角平分线定义④等式性质⑤两直线平行，同位角相等，内错角相等⑥全等三角形的对应角相等2、证线段相等的方法：①中点定义②全等三角形对应边相等③等式的性质3、两种基本图形①线段的等量加等量（或等量减等量）的图形。ABCD由AB=CD可知AC=BD（反之也成立）②角的等量加等量（或等量减等量）的图形AOBCD由∠AOC=∠BOD可知∠AOD=∠BOC(反之也成立） 4、当图形较复杂时，也将复杂图形分解研究ABCDABCBCD分解再见