三角形复习[下学期]

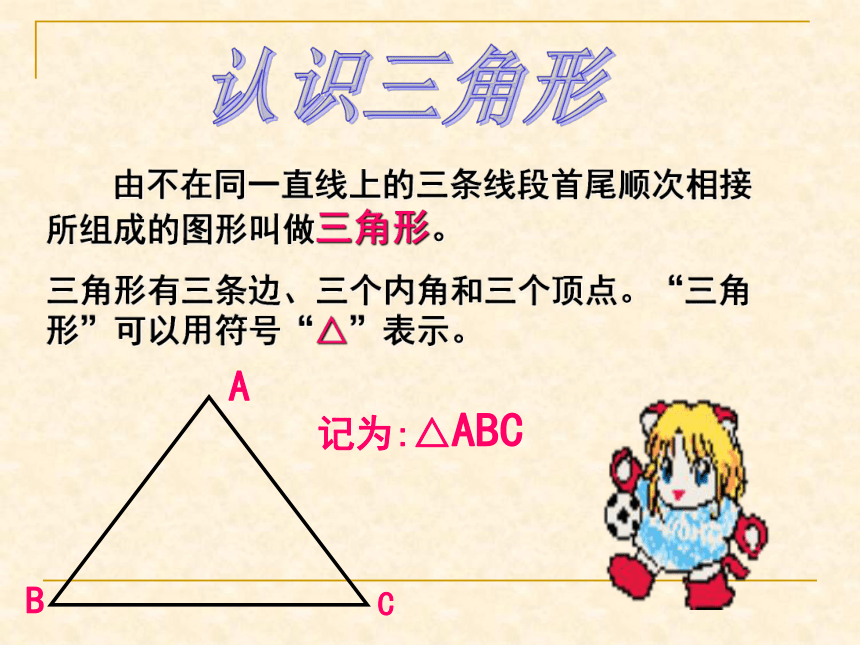
课件14张PPT。三角形 在我们的生活中几乎随处可见三角形。它简单、有趣，也十分有用。三角形可以帮助我们更好的认识周围的世界，可以帮助我们解决很多实际问题……认识三角形 由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
三角形有三条边、三个内角和三个顶点。“三角形”可以用符号“△”表示。记为:△ABC三角形有关概念1、三角形任意两边之和大于第三边。
2、三角形任意两边之差小于第三边。
3、三角形三个内角的和等于180度。
4、直角三角形的两个锐角互余。
5、三角形的三条角平分线交于一点，三条中线交于一点。
6、三角形的三条高所在的直线交于一点。
7、全等图形的形状和大小都相同。
8、全等三角形的对应边相等，对应角相等。探索三角形全等的条件 1、两个能够重合的三角形称为全等三角形。SSS SAS ASA AAS HLSSS SAS（两边夹角） ASA （两角夹边） AAS2、两个三角形全等的条件:3、两个直角三角形全等的条件:三角形三边关系1、三角形两条边分别是2cm，7cm，则第三边c的范围为 。2、等腰三角形的一边长为6cm，另一边长为12cm，则其周长（ ）
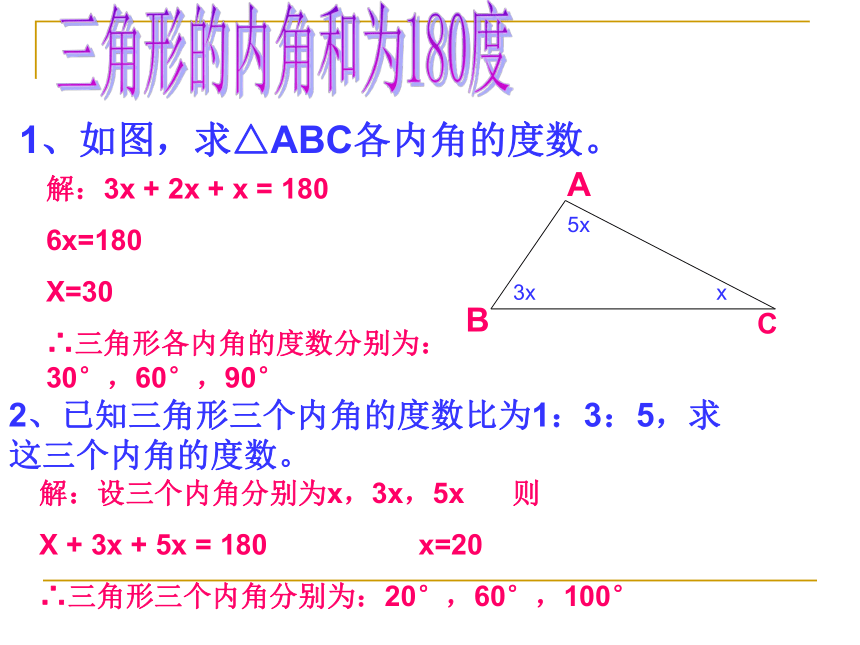
A、24cm B、30cm C、24cM或30cm D、18cm3、（2005 陕西）用7根火柴首尾顺次连结摆成一个三角形，能摆成不同的三角形的个数为 。5＜c＜9B2（3，3，1；2，2，3）三角形的内角和为180度1、如图，求△ABC各内角的度数。2、已知三角形三个内角的度数比为1：3：5，求这三个内角的度数。解：3x + 2x + x = 180
6x=180
X=30
∴三角形各内角的度数分别为：30°，60°，90°解：设三个内角分别为x，3x，5x 则
X + 3x + 5x = 180 x=20
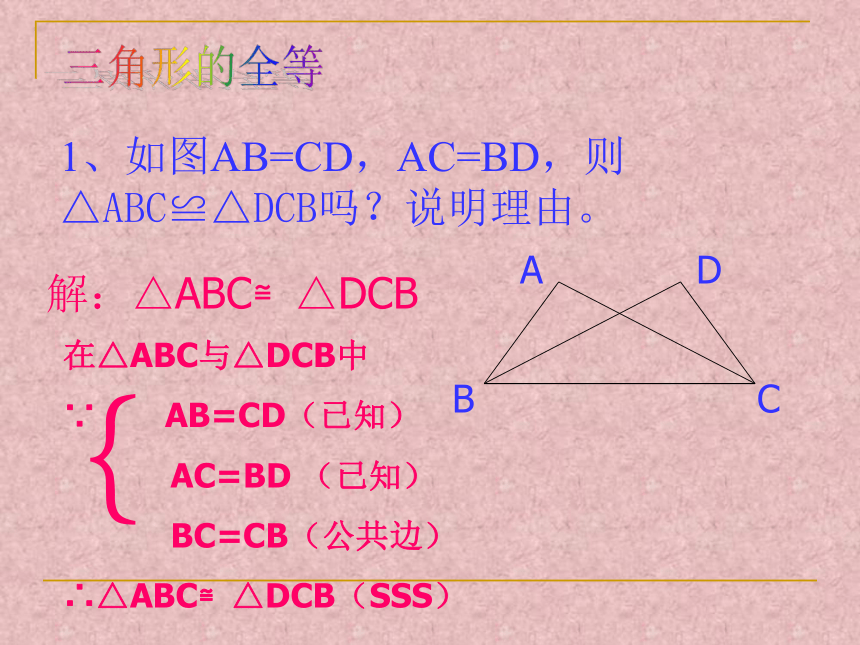
∴三角形三个内角分别为：20°，60°，100°1、如图AB=CD，AC=BD，则△ABC≌△DCB吗？说明理由。 解：△ABC≌△DCB三角形的全等1、（2005·桂林）已知：如图 ∠ABC=∠DCB,AB=DC， 求证:(1)AC=BD;(2)S△AOB = S△DOC 变式议练：证明：（1）在△ABC与△DCB中，
∵ AB=DC （已知）
∠ABC=∠DCB（已知）
BC=CB （公共边）
∴ △ABC≌△DCB（SAS）
∴AC=BD（全等三角形
的对应边相等）（2）∵ △ABC≌△DCB，
∴S △ABC = S △DCB
∴S △ABC－ S△BOC= S △DCB－ S△BOC
即S△AOB = S△DOC
变式议练：2、如图,已知∠ABC=∠DCB,要使△ABC≌△DCB，只需添加一个条件是 。(只需添加一个你认为适合的条件)AB=DC∠A=∠D∠1=∠212隐含条件：BC=CBSASAASASAAB=DE∠ACB=∠F∠A=∠D已知条件:
∠B＝∠DEF，
BC＝EF在△ABC与△ADC中
∵ ∠1＝∠2(已知)
∠B＝∠D(已知)
AC=AC(公共边)
∴ △ABC≌△ADC(AAS)4、如图，已知AB＝AC，BD＝CE。
求证：△ABE≌△ACD。
在△ABE与△ACD中
∵ AB＝AC(已知)
AD=AE(已证)
∠A=∠A(公共角)
∴ △ABE≌△ACD(SAS)证明:∵ AB＝AC，BD＝CE(已知)
∴AD=AE(等式性质)
7、如图，AB，CD交于点E，且AE=DE，EC=EB，试说明：BD=AC解:在△AEC与△DEB中
∵ AE=DE(已知)
EC=EB已知)
∠BED=∠CEA(对顶角相等)
∴ △AEC≌△DEB(SAS)
∴ BD=AC(全等三角形的对应边相等)再见