人教版六年级数学下册 圆柱的表面积(教案)
文档属性
| 名称 | 人教版六年级数学下册 圆柱的表面积(教案) |  | |
| 格式 | docx | ||
| 文件大小 | 87.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 15:10:21 | ||
图片预览


文档简介
《圆柱的表面积》教案
【教学目标】
1. 知识与技能
结合具体情境和操作活动,探索并掌握圆柱侧面积和表面积的计算方法,并能正确计算圆柱的侧 面积和表面积。
2.过程与方法
经历圆柱的侧面积、表面积的公式的发现过程, 体验利用旧知识迁移学习的方法。
3.情感态度与价值观
能根据具体情境, 灵活运用圆柱表面积的计算方法解决生活中一些简单的问题, 体会数学与生活
的联系。 21 教育网
【教学重点】
理解、掌握圆柱表面积计算的公式, 并运用公式正确地计算圆柱表面积。
【教学难点】
推导圆柱表面积计算的公式。
【教学方法】
启发式教学、自主探索、合作交流、讨论法、讲解法。
【课前准备】
多媒体、圆柱模型
【课时安排】
1 课时
【教学过程】
(一)激趣导入
师:同学们, 你们能举出几个圆柱形物体的例子吗?今天老师为同学们带来两个圆柱形物体, 我们一起看一下:(课件出示图片) 21 ·cn ·jy ·com
提问: 哪个圆柱形灯台用的材料多一些? (学生讨论)
猜一猜:圆柱的侧面是怎样做成的?
师小结:右边灯台用的材料多一些, 说明这个圆柱体的表面积大一些。这节课我们一起来研究怎 样求圆柱的表面积。(板书课题) 21cnjy.com
(二) 探究新知
1. 探究圆柱表面积的计算方法,学习例 3。
(1) 出示例 3:出示情境图
师:圆柱的表面积指的是什么?
学生讨论后师总结:圆柱的表面积是指圆柱表面所有部分面积之和。
(2) 合作探索(剪一剪圆柱)
a.圆柱的表面有哪几部分组成?
b.怎样计算圆柱的表面积?
c.圆柱表面积关键是计算哪一部分?
d.圆柱的侧面积怎样计算?
小组合作探索, 师巡视指导。
(3) 汇报交流:
师: 圆柱的侧面是怎样展开的? 展开后是什么图形?
生:圆柱的侧面沿高展开是个长方形。
师:圆柱展开后有几部分,怎样计算圆柱的表面积呢?
生:圆柱的侧面展开后由三部分组成,两个底面和一个侧面。
课件演示:
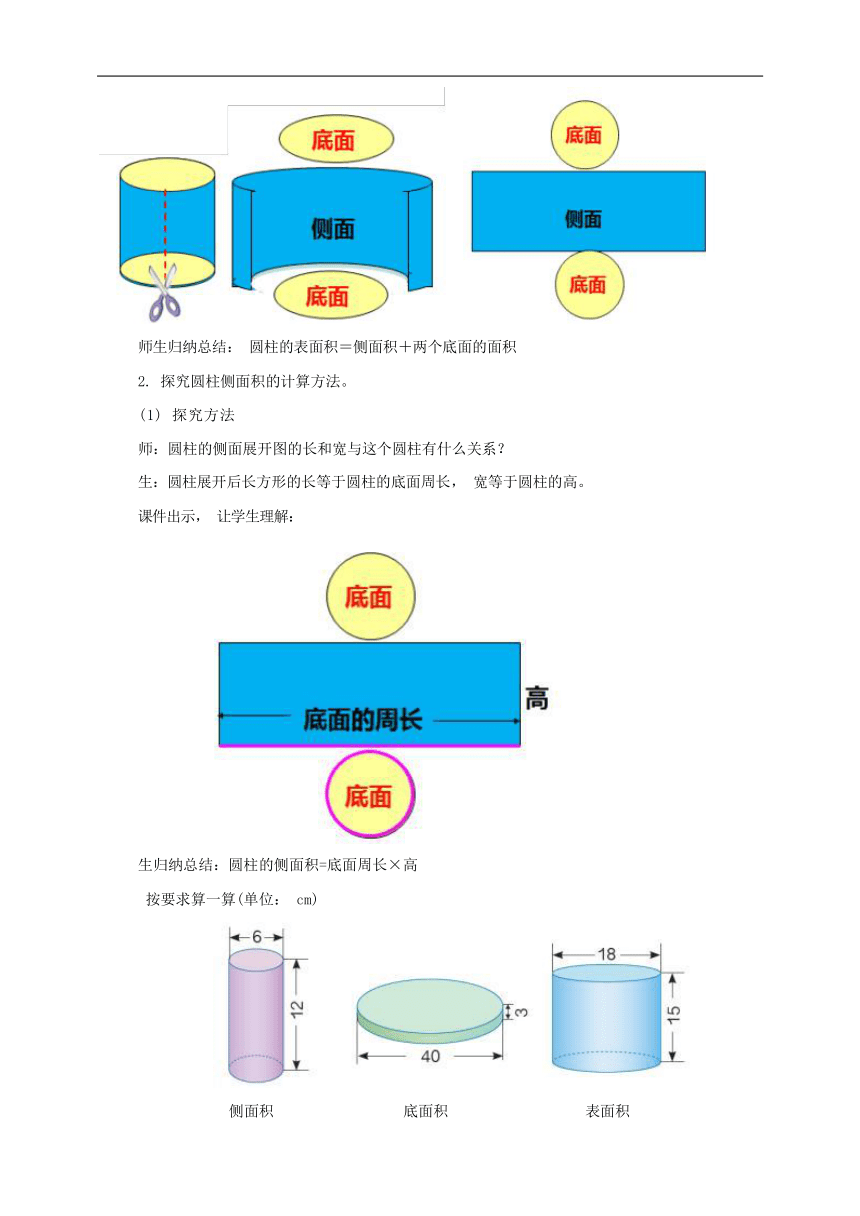
师生归纳总结: 圆柱的表面积=侧面积+两个底面的面积
2. 探究圆柱侧面积的计算方法。
(1) 探究方法
师:圆柱的侧面展开图的长和宽与这个圆柱有什么关系?
生:圆柱展开后长方形的长等于圆柱的底面周长, 宽等于圆柱的高。
课件出示, 让学生理解:
生归纳总结:圆柱的侧面积=底面周长×高
按要求算一算(单位: cm)
侧面积
底面积
表面积 www.21-cn-jy.com
(2) 做一做:
一个鱼缸的侧面是用钢化玻璃制成的。制作这样一 个鱼缸,至少需要多少平方米的钢化玻璃?
3. 表面积的应用, 学习例 4。
课件出示例 4:
一顶圆柱形厨师帽, 高 30 厘米, 冒顶直径 20 厘米, 做这样一顶帽子至少要用多少平方厘米
的面料?
(1) 小组比赛:看哪个小组做得又对又快?
(2) 交流:求帽子用多少面料就是求哪个面的面积?
(3) 师小结: 求至少用多少面料,就是求帽子的侧面积和一个底面积的和。
(4) 汇报解题思路:
先求帽子的侧面积: 3.14 ×20 ×30=1884 (平方厘米)
再求帽顶的面积:3.14 ×(20÷2) 2 =314 (平方厘米)
最后求需要用的材料:1884+314=2198 ≈ 2200 (平方厘米)
答:做这样一顶帽子至少需要用 2200 平方厘米的材料。
(5) 师归纳总结:
实际使用的面料要比计算的结果多一些, 所以这类问题往往用“进一法”取近似值。
在解答实际问题前一定要先进行分析,看它们求的是哪部分面积, 再选择解答的方法。 4.灵活运用:一段圆柱形木头, 截成两段,它的表面积会有什么变化?
(三)课堂练习
谈话: 同学们, 你们学得怎么样了? 我们一起到智慧乐园挑战一下自己吧! 有没有信心呢?
1. 一个圆柱的侧面积是 94.2 平方厘米, 高是 3 厘米,它的底面半径是多少厘米?
2. 小亚做了一个笔筒, 她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?
(四) 拓展提高
一个底面半径是 5 米, 深 10 米的蓄水池, 如果再挖深 3 米, 表面积增加了多少平方米?
(五)课堂总结
师: 通过学习,你有什么收获?
生交流:
1.圆柱的表面积是指圆柱表面所有部分面积之和。
2.圆柱的侧面积=底面周长×高
3.圆柱的表面积=侧面积+两个底面的面积。
4. 在解答表面积时要根据生活实际, 看它们求的是哪部分面积,计算结果要用进一法。
(六)板书设计
圆柱的表面积
圆柱的侧面积=底面周长×高
圆柱的表面积=侧面积+两个底面的面积
计算表面积时根据实际结果要用进一法
【教学反思】
本节课的教学是在学生对圆柱的组成和特征已有初步认识,并且掌握了长方体、正方体表面积 的计算方法的基础上进行的。根据学生的认知基础及培养学生的数学思维能力和空间想象能力,在教 学设计上有以下特点:21 世纪教育网版权所有
1.利用迁移、猜想,理解圆柱表面积的意义。 导入新课,通过比较两个圆柱形灯台的大小, 使学生对圆柱表面积有了初步的理解,为进一步探究圆柱表面积的求法作铺垫。
2.利用演示、分析探究圆柱表面积的求法。 直观演示可以使学生获得丰富的感性材料, 加深 对知识本质的理解, 有利于培养学生的形象思维能力, 因此,在教学中不但要鼓励学生大胆猜想,还 要借助多媒体教学, 帮助学生建立起圆柱各部分之间的联系, 使学生轻松得出结论。
3.联系实际,解决问题。 在实际生活中,应用圆柱的表面积公式解决问题,有时只需要计算 圆柱的侧面积, 有时要计算圆柱的侧面积和一个底面的面积, 因此, 在教学中要引导学生学会把自己 的知识经验及解决问题的策略不断地构建、重组、内化、升华,使感性认识与理性认识同时得到提升。
【教学目标】
1. 知识与技能
结合具体情境和操作活动,探索并掌握圆柱侧面积和表面积的计算方法,并能正确计算圆柱的侧 面积和表面积。
2.过程与方法
经历圆柱的侧面积、表面积的公式的发现过程, 体验利用旧知识迁移学习的方法。
3.情感态度与价值观
能根据具体情境, 灵活运用圆柱表面积的计算方法解决生活中一些简单的问题, 体会数学与生活
的联系。 21 教育网
【教学重点】
理解、掌握圆柱表面积计算的公式, 并运用公式正确地计算圆柱表面积。
【教学难点】
推导圆柱表面积计算的公式。
【教学方法】
启发式教学、自主探索、合作交流、讨论法、讲解法。
【课前准备】
多媒体、圆柱模型
【课时安排】
1 课时
【教学过程】
(一)激趣导入
师:同学们, 你们能举出几个圆柱形物体的例子吗?今天老师为同学们带来两个圆柱形物体, 我们一起看一下:(课件出示图片) 21 ·cn ·jy ·com
提问: 哪个圆柱形灯台用的材料多一些? (学生讨论)
猜一猜:圆柱的侧面是怎样做成的?
师小结:右边灯台用的材料多一些, 说明这个圆柱体的表面积大一些。这节课我们一起来研究怎 样求圆柱的表面积。(板书课题) 21cnjy.com
(二) 探究新知
1. 探究圆柱表面积的计算方法,学习例 3。
(1) 出示例 3:出示情境图
师:圆柱的表面积指的是什么?
学生讨论后师总结:圆柱的表面积是指圆柱表面所有部分面积之和。
(2) 合作探索(剪一剪圆柱)
a.圆柱的表面有哪几部分组成?
b.怎样计算圆柱的表面积?
c.圆柱表面积关键是计算哪一部分?
d.圆柱的侧面积怎样计算?
小组合作探索, 师巡视指导。
(3) 汇报交流:
师: 圆柱的侧面是怎样展开的? 展开后是什么图形?
生:圆柱的侧面沿高展开是个长方形。
师:圆柱展开后有几部分,怎样计算圆柱的表面积呢?
生:圆柱的侧面展开后由三部分组成,两个底面和一个侧面。
课件演示:
师生归纳总结: 圆柱的表面积=侧面积+两个底面的面积
2. 探究圆柱侧面积的计算方法。
(1) 探究方法
师:圆柱的侧面展开图的长和宽与这个圆柱有什么关系?
生:圆柱展开后长方形的长等于圆柱的底面周长, 宽等于圆柱的高。
课件出示, 让学生理解:
生归纳总结:圆柱的侧面积=底面周长×高
按要求算一算(单位: cm)
侧面积
底面积
表面积 www.21-cn-jy.com
(2) 做一做:
一个鱼缸的侧面是用钢化玻璃制成的。制作这样一 个鱼缸,至少需要多少平方米的钢化玻璃?
3. 表面积的应用, 学习例 4。
课件出示例 4:
一顶圆柱形厨师帽, 高 30 厘米, 冒顶直径 20 厘米, 做这样一顶帽子至少要用多少平方厘米
的面料?
(1) 小组比赛:看哪个小组做得又对又快?
(2) 交流:求帽子用多少面料就是求哪个面的面积?
(3) 师小结: 求至少用多少面料,就是求帽子的侧面积和一个底面积的和。
(4) 汇报解题思路:
先求帽子的侧面积: 3.14 ×20 ×30=1884 (平方厘米)
再求帽顶的面积:3.14 ×(20÷2) 2 =314 (平方厘米)
最后求需要用的材料:1884+314=2198 ≈ 2200 (平方厘米)
答:做这样一顶帽子至少需要用 2200 平方厘米的材料。
(5) 师归纳总结:
实际使用的面料要比计算的结果多一些, 所以这类问题往往用“进一法”取近似值。
在解答实际问题前一定要先进行分析,看它们求的是哪部分面积, 再选择解答的方法。 4.灵活运用:一段圆柱形木头, 截成两段,它的表面积会有什么变化?
(三)课堂练习
谈话: 同学们, 你们学得怎么样了? 我们一起到智慧乐园挑战一下自己吧! 有没有信心呢?
1. 一个圆柱的侧面积是 94.2 平方厘米, 高是 3 厘米,它的底面半径是多少厘米?
2. 小亚做了一个笔筒, 她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?
(四) 拓展提高
一个底面半径是 5 米, 深 10 米的蓄水池, 如果再挖深 3 米, 表面积增加了多少平方米?
(五)课堂总结
师: 通过学习,你有什么收获?
生交流:
1.圆柱的表面积是指圆柱表面所有部分面积之和。
2.圆柱的侧面积=底面周长×高
3.圆柱的表面积=侧面积+两个底面的面积。
4. 在解答表面积时要根据生活实际, 看它们求的是哪部分面积,计算结果要用进一法。
(六)板书设计
圆柱的表面积
圆柱的侧面积=底面周长×高
圆柱的表面积=侧面积+两个底面的面积
计算表面积时根据实际结果要用进一法
【教学反思】
本节课的教学是在学生对圆柱的组成和特征已有初步认识,并且掌握了长方体、正方体表面积 的计算方法的基础上进行的。根据学生的认知基础及培养学生的数学思维能力和空间想象能力,在教 学设计上有以下特点:21 世纪教育网版权所有
1.利用迁移、猜想,理解圆柱表面积的意义。 导入新课,通过比较两个圆柱形灯台的大小, 使学生对圆柱表面积有了初步的理解,为进一步探究圆柱表面积的求法作铺垫。
2.利用演示、分析探究圆柱表面积的求法。 直观演示可以使学生获得丰富的感性材料, 加深 对知识本质的理解, 有利于培养学生的形象思维能力, 因此,在教学中不但要鼓励学生大胆猜想,还 要借助多媒体教学, 帮助学生建立起圆柱各部分之间的联系, 使学生轻松得出结论。
3.联系实际,解决问题。 在实际生活中,应用圆柱的表面积公式解决问题,有时只需要计算 圆柱的侧面积, 有时要计算圆柱的侧面积和一个底面的面积, 因此, 在教学中要引导学生学会把自己 的知识经验及解决问题的策略不断地构建、重组、内化、升华,使感性认识与理性认识同时得到提升。
