8.1.1棱柱、棱锥、棱台2022-2023学年高一数学同步精讲 课件(共36张PPT)
文档属性
| 名称 | 8.1.1棱柱、棱锥、棱台2022-2023学年高一数学同步精讲 课件(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 18:32:15 | ||
图片预览










文档简介
(共36张PPT)
立体几何初步
章前语
立体几何研究什么?
本章主要学习的内容
学习本章时应要注意什么?
立体几何是研究现实世界中物体的形状、大小与位置关系的数学分支,在解决实际问题中有着广泛的应用.在小学和初中, 我们已经认识了一些从现实物体中抽象的立体图形,你能在图中找到它们吗?
立体图形各式各样、千姿百态,如何认识和把握它们呢?本章我们将从对空间几何体的整体观察入手,研究它们的结构特征,学习它们的表示方法,了解它们的表面积和体积的计算方 法;借助长方体,从构成立体图形的基本元素———点、直线、平面入手,研究它们的性质以及相互之间的位置关系,特别是对直线、平面的平行与垂直的关系展开研究,从而进一步认识空间几何体的性质.
立体图形是由现实物体抽象而成的.直观感知、操作确认、 推理论证、度量计算,是认识立体图形的基本方法.由整体到局部,由局部再到整体,是认识立体图形的有效途径。学习本章内容要注意观察,并善于想象。
§8.1.1 棱柱、棱锥、棱台
§8.1 基本立体图形(1)
空间几何体
特殊的多面体
典型例题分析
小结及随堂练习
空间几何体
01
情境引入
空间几何体
在我们周围存在着各种各样的物体,它们都占据着空间的一部分。如果只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.
定义
本节我们主要从几何体的组成元素及其相互关系的角度,
认识几种最基本的空间几何体
空间几何体
如图,这些图片中的物体具有怎样的形状?如何描述它们的形状?
在日常生活中,我们把这些物体的形状叫做什么?
空间几何体
在上图中,可以发现:
①纸箱、金字塔、茶叶盒、水晶萤石、储物箱等物体有相同的特点:
围成它们的每个面都是平面图形,并且都是平面多边形;
②纸杯、腰鼓、奶粉罐、篮球和足球、铅锤等物体也有相同的特点:
围成它们的面不全是平面图形,有些面是曲面.
观察一个物体,将它抽象成空间几何体,并描述它的结构特征,应先从整体入手,想象围成物体的每个面的形状、面与面之间的关系,并注意利用平面图形的知识
学习新知
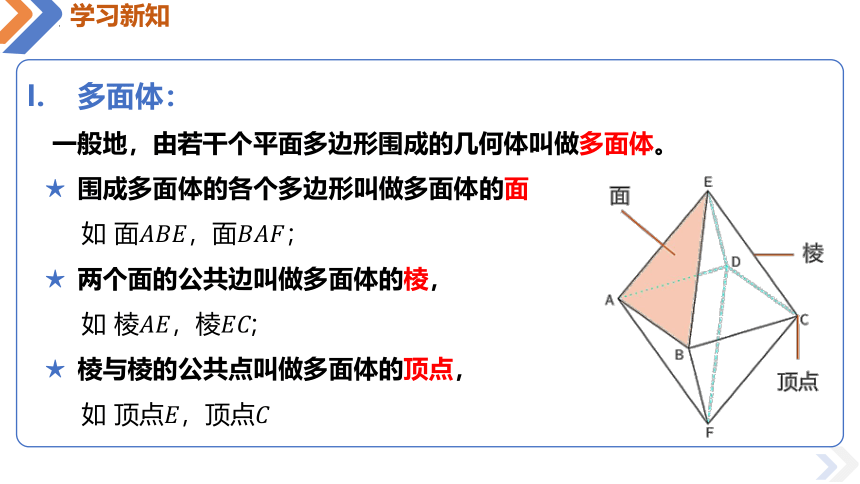
多面体:
一般地,由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面
如 面,面
两个面的公共边叫做多面体的棱,
如 棱,棱;
棱与棱的公共点叫做多面体的顶点,
如 顶点,顶点
学习新知
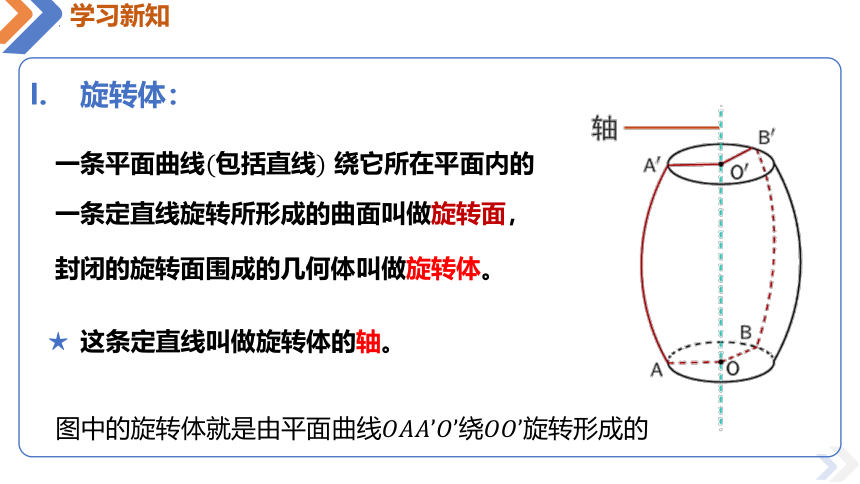
旋转体:
一条平面曲线包括直线 绕它所在平面内的
一条定直线旋转所形成的曲面叫做旋转面,
封闭的旋转面围成的几何体叫做旋转体。
这条定直线叫做旋转体的轴。
图中的旋转体就是由平面曲线绕旋转形成的
特殊的多面体
02
1.棱柱
观察下图中的长方体,它的每个面是什么样的多边形
不同的面之间有什么位置关系
可以发现:长方体的每个面都是平行四边形(矩形),并且相对的两个面,如面和面’,给我们以平行的形象,如同教室的地面和天花板一样。
棱柱:
一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
在棱柱中,
两个互相平行的面叫做棱柱的底面
它们是全等的多边形;
其余各面叫做棱柱的侧面,
它们都是平行四边形;
相邻侧面的公共边叫做棱柱的侧棱;
侧面与底面的公共顶点叫做棱柱的顶点。
1.棱柱
棱柱
1.棱柱
满足“ 有两个面相互平行,其余各面都是平行四边形的几何体 ”这样说法的还有右图的情况,如图所示,所以定义中不能简单描述成“其余各面都是平行四边形 。.
为什么定义中要说‘‘其余各面都是四边形,并且相邻两个四边形的公共边都相互平行'',而不简单的只说 “ 其余各面是平行四边形呢 ” ?
棱柱的结构特征
两底面互相平行且全等
各侧面都是平行四边形
各侧棱互相平行且相等
1.棱柱
棱柱的分类
一、按棱柱底面边数分类:
三棱柱,四棱柱,五棱柱......;
五棱柱:底面是五边形.
四棱柱:底面是四边形.
三棱柱:底面是三角形.
直棱柱,斜棱柱;
二、按侧棱与底面的位置关系分类:
斜棱柱:侧棱不垂直于底面.
直棱柱:侧棱与底面垂直.
1.棱柱
特殊的棱柱
① 正棱柱:
底面是正多边形的直棱柱叫做正棱柱.
正五棱柱
正四棱柱
正三棱柱
② 平行六面体:
底面是平行四边形的四棱柱叫做平行六面体.
平行六面体
斜棱柱
棱柱
直棱柱
侧棱垂直底面
侧棱不垂直底面
底面是平行四边形
底面是正边形
正棱柱
底面是矩形
长方体
正方体
各棱长都相等
2.棱锥
棱锥:
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
这个多边形面叫棱锥的底面
有公共顶点的各个三角形面叫做棱锥的侧面,
相邻侧面的公共边叫做棱锥的侧棱;
各侧面的公共顶点叫做棱锥的顶点。
棱锥
2.棱锥
注意:一定要三角形交于同一个顶点,
比如右图的两张图片就不符和要求 。
有一个面是多边形,其余各面都是三角形的几何体就是棱锥吗?
棱锥的结构特征
仅有一个底面是多边形
侧面都是三角形
各侧面有且只有一个公共顶点
2.棱锥
棱锥的分类
一、按棱锥底面边数分类:
三棱锥,四棱锥,五棱锥......;
二、特殊的棱锥:
五棱锥:底面是五边形.
四棱锥:底面是四边形.
三棱椎:底面是三角形.
三棱锥又叫四面体.
底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥
3.棱台
棱台:
用一个平行于棱锥底面的平面去截棱锥,我们把底面和截面之间那部分多面体叫做棱台。
在棱台中,
原棱锥的底面和截面分别叫做棱台的上底面和下底面
其余各面叫做棱台的侧面,
相邻侧面的公共边叫做棱柱的侧棱;
侧面与底面的公共顶点叫做棱台的顶点。
棱台
3.棱台
图①中多面体侧棱延长线不相交于同一点;
图②中多面体不是由棱锥截得的;
图③中多面体虽是由棱锥截得的,但截面与底面不平行
辨析:右图所示的多面体是不是棱台?
棱台的结构特征
上下底面是互相平行且相似的多边形
侧面都是梯形
各侧棱的延长线交于一点
3.棱台
辨析2:若一个几何体有两个面平行,且其余各面均为梯形,则它一
定是棱台吗?
未必是棱台,因为它们的侧棱延长后不一定交于一点,如图,用一个平行于楔形几何体底面的平面去截楔形几何体,截面与底面之间的几何体虽有两个面平行,其余各面是梯形,但它不是棱台。所以看一个几何体是否是棱台,不仅要看是否有两个面平行,其余各面是否是梯形,还有看其侧棱延长后是否交于一点 .
3.棱台
棱台的分类
一、按棱台底面边数分类:
三棱台,四棱台,五棱台......;
二、特殊的棱台:
由正棱锥截得的棱台,上下底面都是正多边形,侧面都是全等的等腰梯形的棱台叫做正棱台。
五棱台:由五棱锥截得的棱台
四棱台:由四棱锥截得的棱台
三棱台:由三棱锥截得的棱台
融会贯通
例1.将下列各类几何体之间的关系用Venn图表示出来:
多面体,长方体,棱柱棱锥,棱台,直棱柱,四面体,平行六面体
解:如图所示
典型例题分析
03
典例精析
题型一:棱柱的结构特点
例2.下列说法正确的是( ).
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有9条侧棱,9个侧面,侧面均为平行四边形
D
例3.下列命题中,正确的是( ).
A.棱柱中所有的侧棱都相交于一点
B.棱柱中互相平行的两个面叫做棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱相等,侧面是平行四边形
D
典例精析
题型一:棱柱的结构特点
(1)看“面”:
观察这个多面体是否有两个互相平行的面,其余各面都是四边形
(2)看“线” :
在察每相邻两个四边形的公共边是否平行
(3) 举反例 :
通过举反例,如与常见几何体或实物模型、图片等不吻合,给予排除
思维升华:准确认识棱柱的结构特征
典例精析
题型二:棱锥、棱台的结构特点
例4.下面是关于棱锥、棱台的四种说法:
①棱锥的侧面只能是三角形; ②棱台的侧面一定不会是平行四边形;
③由四个面围成的封闭图形只能是三棱锥;
④棱锥被平面截成的两部分不可能都是棱锥.
其中说法错误的是( ).
A.① B.② C.③ D.④
D
例5. 下列命题中,正确的是( ).
A.棱柱中所有的侧棱都相交于一点
B.棱柱中互相平行的两个面叫做棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱相等,侧面是平行四边形
A
典例精析
题型二:棱锥、棱台的结构特点
思维升华:准确认识棱锥、棱台的结构特征
棱锥 棱台
看“底面” 只有一个面是多边形, 此面即为底面 有两个互相平行的相似多边形,
即为底面
看“侧面” 都有一个公共顶点的三角形 都是梯形
看“侧棱” 相交于一点 延长后相交于一点
小结及随堂练习
04
随堂练习
1.判断下列命题是否正确,正确的在括号内画 “√”,错误的画“×”.
(1)长方体是四棱柱,直四棱柱是长方体. ( )
(2)四棱柱、四棱台、五棱锥都是六面体. ( )
2.填空题
(1)一个几何体由7个面围成,其中两个面是互相平行且全等的五边形,其他各面都是全等的矩形, 则这个几何体是_________.
(2)一个多面体最少有________个面,此时这个多面体是_______.
课时达标检测20(必做)
预习下一课(选做)
立体几何初步
章前语
立体几何研究什么?
本章主要学习的内容
学习本章时应要注意什么?
立体几何是研究现实世界中物体的形状、大小与位置关系的数学分支,在解决实际问题中有着广泛的应用.在小学和初中, 我们已经认识了一些从现实物体中抽象的立体图形,你能在图中找到它们吗?
立体图形各式各样、千姿百态,如何认识和把握它们呢?本章我们将从对空间几何体的整体观察入手,研究它们的结构特征,学习它们的表示方法,了解它们的表面积和体积的计算方 法;借助长方体,从构成立体图形的基本元素———点、直线、平面入手,研究它们的性质以及相互之间的位置关系,特别是对直线、平面的平行与垂直的关系展开研究,从而进一步认识空间几何体的性质.
立体图形是由现实物体抽象而成的.直观感知、操作确认、 推理论证、度量计算,是认识立体图形的基本方法.由整体到局部,由局部再到整体,是认识立体图形的有效途径。学习本章内容要注意观察,并善于想象。
§8.1.1 棱柱、棱锥、棱台
§8.1 基本立体图形(1)
空间几何体
特殊的多面体
典型例题分析
小结及随堂练习
空间几何体
01
情境引入
空间几何体
在我们周围存在着各种各样的物体,它们都占据着空间的一部分。如果只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.
定义
本节我们主要从几何体的组成元素及其相互关系的角度,
认识几种最基本的空间几何体
空间几何体
如图,这些图片中的物体具有怎样的形状?如何描述它们的形状?
在日常生活中,我们把这些物体的形状叫做什么?
空间几何体
在上图中,可以发现:
①纸箱、金字塔、茶叶盒、水晶萤石、储物箱等物体有相同的特点:
围成它们的每个面都是平面图形,并且都是平面多边形;
②纸杯、腰鼓、奶粉罐、篮球和足球、铅锤等物体也有相同的特点:
围成它们的面不全是平面图形,有些面是曲面.
观察一个物体,将它抽象成空间几何体,并描述它的结构特征,应先从整体入手,想象围成物体的每个面的形状、面与面之间的关系,并注意利用平面图形的知识
学习新知
多面体:
一般地,由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面
如 面,面
两个面的公共边叫做多面体的棱,
如 棱,棱;
棱与棱的公共点叫做多面体的顶点,
如 顶点,顶点
学习新知
旋转体:
一条平面曲线包括直线 绕它所在平面内的
一条定直线旋转所形成的曲面叫做旋转面,
封闭的旋转面围成的几何体叫做旋转体。
这条定直线叫做旋转体的轴。
图中的旋转体就是由平面曲线绕旋转形成的
特殊的多面体
02
1.棱柱
观察下图中的长方体,它的每个面是什么样的多边形
不同的面之间有什么位置关系
可以发现:长方体的每个面都是平行四边形(矩形),并且相对的两个面,如面和面’,给我们以平行的形象,如同教室的地面和天花板一样。
棱柱:
一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
在棱柱中,
两个互相平行的面叫做棱柱的底面
它们是全等的多边形;
其余各面叫做棱柱的侧面,
它们都是平行四边形;
相邻侧面的公共边叫做棱柱的侧棱;
侧面与底面的公共顶点叫做棱柱的顶点。
1.棱柱
棱柱
1.棱柱
满足“ 有两个面相互平行,其余各面都是平行四边形的几何体 ”这样说法的还有右图的情况,如图所示,所以定义中不能简单描述成“其余各面都是平行四边形 。.
为什么定义中要说‘‘其余各面都是四边形,并且相邻两个四边形的公共边都相互平行'',而不简单的只说 “ 其余各面是平行四边形呢 ” ?
棱柱的结构特征
两底面互相平行且全等
各侧面都是平行四边形
各侧棱互相平行且相等
1.棱柱
棱柱的分类
一、按棱柱底面边数分类:
三棱柱,四棱柱,五棱柱......;
五棱柱:底面是五边形.
四棱柱:底面是四边形.
三棱柱:底面是三角形.
直棱柱,斜棱柱;
二、按侧棱与底面的位置关系分类:
斜棱柱:侧棱不垂直于底面.
直棱柱:侧棱与底面垂直.
1.棱柱
特殊的棱柱
① 正棱柱:
底面是正多边形的直棱柱叫做正棱柱.
正五棱柱
正四棱柱
正三棱柱
② 平行六面体:
底面是平行四边形的四棱柱叫做平行六面体.
平行六面体
斜棱柱
棱柱
直棱柱
侧棱垂直底面
侧棱不垂直底面
底面是平行四边形
底面是正边形
正棱柱
底面是矩形
长方体
正方体
各棱长都相等
2.棱锥
棱锥:
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
这个多边形面叫棱锥的底面
有公共顶点的各个三角形面叫做棱锥的侧面,
相邻侧面的公共边叫做棱锥的侧棱;
各侧面的公共顶点叫做棱锥的顶点。
棱锥
2.棱锥
注意:一定要三角形交于同一个顶点,
比如右图的两张图片就不符和要求 。
有一个面是多边形,其余各面都是三角形的几何体就是棱锥吗?
棱锥的结构特征
仅有一个底面是多边形
侧面都是三角形
各侧面有且只有一个公共顶点
2.棱锥
棱锥的分类
一、按棱锥底面边数分类:
三棱锥,四棱锥,五棱锥......;
二、特殊的棱锥:
五棱锥:底面是五边形.
四棱锥:底面是四边形.
三棱椎:底面是三角形.
三棱锥又叫四面体.
底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥
3.棱台
棱台:
用一个平行于棱锥底面的平面去截棱锥,我们把底面和截面之间那部分多面体叫做棱台。
在棱台中,
原棱锥的底面和截面分别叫做棱台的上底面和下底面
其余各面叫做棱台的侧面,
相邻侧面的公共边叫做棱柱的侧棱;
侧面与底面的公共顶点叫做棱台的顶点。
棱台
3.棱台
图①中多面体侧棱延长线不相交于同一点;
图②中多面体不是由棱锥截得的;
图③中多面体虽是由棱锥截得的,但截面与底面不平行
辨析:右图所示的多面体是不是棱台?
棱台的结构特征
上下底面是互相平行且相似的多边形
侧面都是梯形
各侧棱的延长线交于一点
3.棱台
辨析2:若一个几何体有两个面平行,且其余各面均为梯形,则它一
定是棱台吗?
未必是棱台,因为它们的侧棱延长后不一定交于一点,如图,用一个平行于楔形几何体底面的平面去截楔形几何体,截面与底面之间的几何体虽有两个面平行,其余各面是梯形,但它不是棱台。所以看一个几何体是否是棱台,不仅要看是否有两个面平行,其余各面是否是梯形,还有看其侧棱延长后是否交于一点 .
3.棱台
棱台的分类
一、按棱台底面边数分类:
三棱台,四棱台,五棱台......;
二、特殊的棱台:
由正棱锥截得的棱台,上下底面都是正多边形,侧面都是全等的等腰梯形的棱台叫做正棱台。
五棱台:由五棱锥截得的棱台
四棱台:由四棱锥截得的棱台
三棱台:由三棱锥截得的棱台
融会贯通
例1.将下列各类几何体之间的关系用Venn图表示出来:
多面体,长方体,棱柱棱锥,棱台,直棱柱,四面体,平行六面体
解:如图所示
典型例题分析
03
典例精析
题型一:棱柱的结构特点
例2.下列说法正确的是( ).
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有9条侧棱,9个侧面,侧面均为平行四边形
D
例3.下列命题中,正确的是( ).
A.棱柱中所有的侧棱都相交于一点
B.棱柱中互相平行的两个面叫做棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱相等,侧面是平行四边形
D
典例精析
题型一:棱柱的结构特点
(1)看“面”:
观察这个多面体是否有两个互相平行的面,其余各面都是四边形
(2)看“线” :
在察每相邻两个四边形的公共边是否平行
(3) 举反例 :
通过举反例,如与常见几何体或实物模型、图片等不吻合,给予排除
思维升华:准确认识棱柱的结构特征
典例精析
题型二:棱锥、棱台的结构特点
例4.下面是关于棱锥、棱台的四种说法:
①棱锥的侧面只能是三角形; ②棱台的侧面一定不会是平行四边形;
③由四个面围成的封闭图形只能是三棱锥;
④棱锥被平面截成的两部分不可能都是棱锥.
其中说法错误的是( ).
A.① B.② C.③ D.④
D
例5. 下列命题中,正确的是( ).
A.棱柱中所有的侧棱都相交于一点
B.棱柱中互相平行的两个面叫做棱柱的底面
C.棱柱的侧面是平行四边形,而底面不是平行四边形
D.棱柱的侧棱相等,侧面是平行四边形
A
典例精析
题型二:棱锥、棱台的结构特点
思维升华:准确认识棱锥、棱台的结构特征
棱锥 棱台
看“底面” 只有一个面是多边形, 此面即为底面 有两个互相平行的相似多边形,
即为底面
看“侧面” 都有一个公共顶点的三角形 都是梯形
看“侧棱” 相交于一点 延长后相交于一点
小结及随堂练习
04
随堂练习
1.判断下列命题是否正确,正确的在括号内画 “√”,错误的画“×”.
(1)长方体是四棱柱,直四棱柱是长方体. ( )
(2)四棱柱、四棱台、五棱锥都是六面体. ( )
2.填空题
(1)一个几何体由7个面围成,其中两个面是互相平行且全等的五边形,其他各面都是全等的矩形, 则这个几何体是_________.
(2)一个多面体最少有________个面,此时这个多面体是_______.
课时达标检测20(必做)
预习下一课(选做)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
