单项式与多项式相乘[[上学期]
图片预览








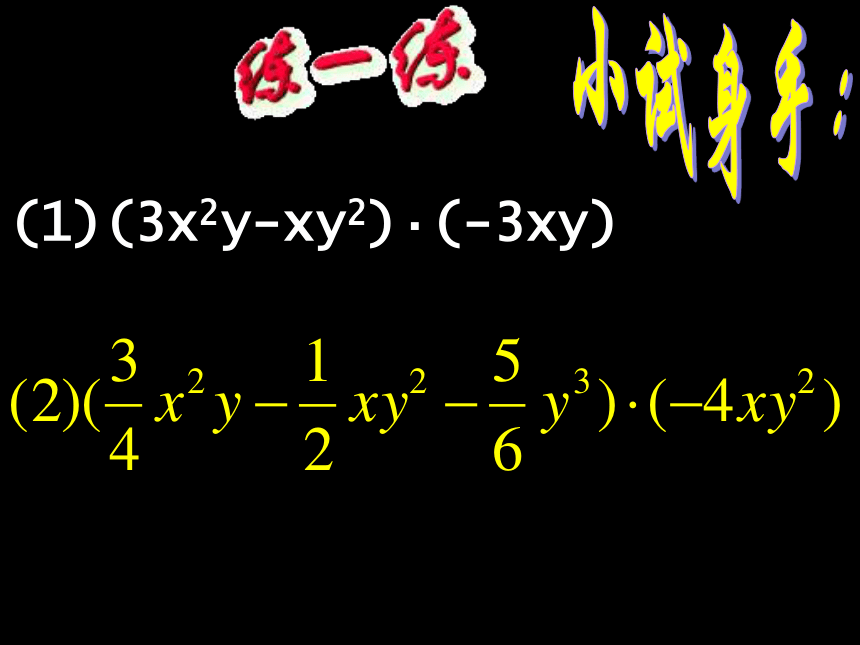
文档简介
课件24张PPT。课题:单项式与多项式相乘2003年11月(-2a)?(2a2-3a+1)=(-2a)?2a2+(-2a)?(-3a)+(-2a)?1=-4a3+6a2-2a(乘法分配律)(单项式与单项式相乘)怎样叙述单项式与多项式相乘的法则? m(a+b+c)=ma+mb+mc
(m、a、b、c都是单项式)单项式与多项式相乘法则 单项式与多项式相乘,就是用单项式与去乘多项式的每一项,再把所得的积相加例1 计算:(1)(-4x)·(2x2+3x-1); 解: (-4x)·(2x2+3x-1)=(-4x)·(2x2)+(-4x)·3x+(-4x)·(-1)=-8x3-12x2+4x; 注意(-1)这项不要漏乘,也不要当成是1; 例1 计算:几点注意:1.单项式乘多项式的结果仍是多项式,
积的项数与原多项式的项数相同。2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负 3.不要出现漏乘现象,运算要有顺序。单项式与多项式相乘时,分两个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算。(1)(3x2y-xy2)·(-3xy) 小试身手: 我你难不倒请同位根据
单项式与多项式相乘法则
自编习题互测 例2 计算:-2a2·(ab+b2)-5a(a2b-ab2) 解:原式=-a3b-2a2b2-5a3b+5a2b2=-a3b-2a2b2-5a3b+5a2b2注意:
1.将2a2与5a前面的“-”看成性质符号
2.单项式与多项式相乘的结果中,应将同类项合并。 =-6a3b+3a2b2 yn(yn +9y-12)–3(3yn+1-4yn),
其中y=-3,n=2.解:yn(yn + 9y-12)–3(3yn+1-4yn)=y2n+9yn+1-12yn–9yn+1+12yn=y2n当y=-3,n=2时,原式=(-3)2×2=(-3)4=81化简求值: 这节课我们学习了单项式与多项式相乘的运算法则,你有何新的收获和体会?你来总结七嘴八舌说一说小结1、单项式与多项式相乘的依据是乘法对加法的分配律
2、单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数相同,注意不要漏乘项
3、积的每一项的符号由原多项式各项符号和单项式的符号来决定形成性测试一.判断× ×√1.m(a+b+c+d)=ma+b+c+d( )( )3.(-2x)?(ax+b-3)=-2ax2-2bx-6x( ) ×4.一个单项式乘以一个多项式,所得的结果
仍是一个多项式( )1.单项式与多项式相乘,就是用单项式去乘
多项式的________,再把所得的积________二.填空2.4(a-b+1)=___________________每一项相加4a-4b+43.3x(2x-y2)=___________________6x2-3xy24.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz5.(-2a2)2(-a-2b+c)=___________________-4a5-8a4b+4a4c三.选择下列计算错误的是( )
(A)5x(2x2-y)=10x3-5xy
(B)-3xa+b ?4xa-b=-12x2a
(C)2a2b?4ab2=8a3b3
(D)(-xn-1y2)?(-xym)2=xnym+2 D=(-xn-1y2)?(x2y2m)=-xn+1y2m+22x一个长方体的长、宽、高分别是2x、 x、
3x-5,它的体积等于( )解:(3x-5)·2x·x
=2x2·(3x-5)
=6x3-10x27x-(x–3)x–3x(2–x)=(2x+1)x+6解:去括号,得
7x–x2+3x–6x+3x2=2x2+x+6移项,得
7x–x2+3x–6x+3x2-2x2-x=6合并同类项,得 3x = 6系数化为1,得 x = 2 解方程 (-2ab)3(5a2b–0.5ab2+0.25b3)解:原式=(-8a3b3)(5a2b–0.5ab2+0.25b3) =(-8a3b3)·(5a2b)+(-8a3b3)·(-0.5ab2)
+(-8a3b3)·0.25b3) =-40a5b4+4a4b5–2a3b6说明:先进行乘方运算,再进行单项式与多项式的乘法运算。计算:计算:x[x(x-1)-1]解法一: x [ x(x - 1)- 1] 解法二:x[ x(x-1)-1 ]=x[(x2–x)-1]=x(x2–x–1)说明:先去小括号,再去中括号。=x3–x2-x=x3–x2-x= x?x(x-1)-x=x2(x-1)-x说明:先把x(x – 1)看成整体,按乘法对加法的分配律去掉中括号,再去掉小括号。例7 如图,计算图中阴影部分的面积.AB=7a,
BC=6bABCDEFGH 分析:阴影部分即长方形ABCD减去
以下四部分:梯形ADGF,△ GCF,△ AHE,
梯形HBCEABCDEFGHAB=7a,
BC=6b
解:阴影部分的面积为:选作题:
设p = x – 1,
计算p ? (xn+xn-1+xn-2+…+x+1)
(m、a、b、c都是单项式)单项式与多项式相乘法则 单项式与多项式相乘,就是用单项式与去乘多项式的每一项,再把所得的积相加例1 计算:(1)(-4x)·(2x2+3x-1); 解: (-4x)·(2x2+3x-1)=(-4x)·(2x2)+(-4x)·3x+(-4x)·(-1)=-8x3-12x2+4x; 注意(-1)这项不要漏乘,也不要当成是1; 例1 计算:几点注意:1.单项式乘多项式的结果仍是多项式,
积的项数与原多项式的项数相同。2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负 3.不要出现漏乘现象,运算要有顺序。单项式与多项式相乘时,分两个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算。(1)(3x2y-xy2)·(-3xy) 小试身手: 我你难不倒请同位根据
单项式与多项式相乘法则
自编习题互测 例2 计算:-2a2·(ab+b2)-5a(a2b-ab2) 解:原式=-a3b-2a2b2-5a3b+5a2b2=-a3b-2a2b2-5a3b+5a2b2注意:
1.将2a2与5a前面的“-”看成性质符号
2.单项式与多项式相乘的结果中,应将同类项合并。 =-6a3b+3a2b2 yn(yn +9y-12)–3(3yn+1-4yn),
其中y=-3,n=2.解:yn(yn + 9y-12)–3(3yn+1-4yn)=y2n+9yn+1-12yn–9yn+1+12yn=y2n当y=-3,n=2时,原式=(-3)2×2=(-3)4=81化简求值: 这节课我们学习了单项式与多项式相乘的运算法则,你有何新的收获和体会?你来总结七嘴八舌说一说小结1、单项式与多项式相乘的依据是乘法对加法的分配律
2、单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数相同,注意不要漏乘项
3、积的每一项的符号由原多项式各项符号和单项式的符号来决定形成性测试一.判断× ×√1.m(a+b+c+d)=ma+b+c+d( )( )3.(-2x)?(ax+b-3)=-2ax2-2bx-6x( ) ×4.一个单项式乘以一个多项式,所得的结果
仍是一个多项式( )1.单项式与多项式相乘,就是用单项式去乘
多项式的________,再把所得的积________二.填空2.4(a-b+1)=___________________每一项相加4a-4b+43.3x(2x-y2)=___________________6x2-3xy24.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz5.(-2a2)2(-a-2b+c)=___________________-4a5-8a4b+4a4c三.选择下列计算错误的是( )
(A)5x(2x2-y)=10x3-5xy
(B)-3xa+b ?4xa-b=-12x2a
(C)2a2b?4ab2=8a3b3
(D)(-xn-1y2)?(-xym)2=xnym+2 D=(-xn-1y2)?(x2y2m)=-xn+1y2m+22x一个长方体的长、宽、高分别是2x、 x、
3x-5,它的体积等于( )解:(3x-5)·2x·x
=2x2·(3x-5)
=6x3-10x27x-(x–3)x–3x(2–x)=(2x+1)x+6解:去括号,得
7x–x2+3x–6x+3x2=2x2+x+6移项,得
7x–x2+3x–6x+3x2-2x2-x=6合并同类项,得 3x = 6系数化为1,得 x = 2 解方程 (-2ab)3(5a2b–0.5ab2+0.25b3)解:原式=(-8a3b3)(5a2b–0.5ab2+0.25b3) =(-8a3b3)·(5a2b)+(-8a3b3)·(-0.5ab2)
+(-8a3b3)·0.25b3) =-40a5b4+4a4b5–2a3b6说明:先进行乘方运算,再进行单项式与多项式的乘法运算。计算:计算:x[x(x-1)-1]解法一: x [ x(x - 1)- 1] 解法二:x[ x(x-1)-1 ]=x[(x2–x)-1]=x(x2–x–1)说明:先去小括号,再去中括号。=x3–x2-x=x3–x2-x= x?x(x-1)-x=x2(x-1)-x说明:先把x(x – 1)看成整体,按乘法对加法的分配律去掉中括号,再去掉小括号。例7 如图,计算图中阴影部分的面积.AB=7a,
BC=6bABCDEFGH 分析:阴影部分即长方形ABCD减去
以下四部分:梯形ADGF,△ GCF,△ AHE,
梯形HBCEABCDEFGHAB=7a,
BC=6b
解:阴影部分的面积为:选作题:
设p = x – 1,
计算p ? (xn+xn-1+xn-2+…+x+1)
