《比例的认识》(课件)-六年级下册数学北师大版(共23张PPT)
文档属性
| 名称 | 《比例的认识》(课件)-六年级下册数学北师大版(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 908.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 05:44:56 | ||
图片预览







文档简介
(共23张PPT)
比例的认识
1.在具体情境中,理解比例的意义和基本性质,会运用比例的意义和基本性质正确判断两个比能否组成比例。
2.在探索比例的意义和基本性质的过程中发展推理能力。
3.通过自主学习,经历探究的过程,体验成功的快乐。
学习目标
1、请同学们回忆一下,上学期我们学过的比的知识,谁能说说什么叫作比?
2、举例说明什么是比的前项、后项和比值。
3、化简下列各比。
16:4 25:5
4、求下面各比的比值。
: 0.81:0.9
复习回顾
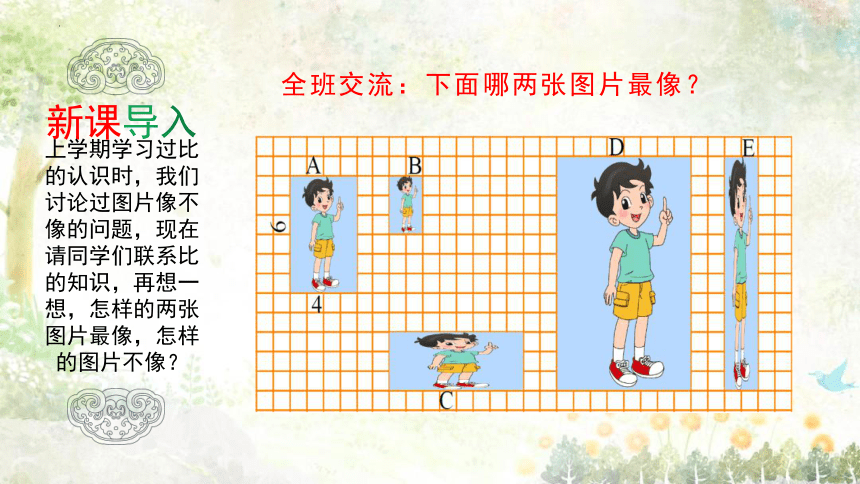
全班交流:下面哪两张图片最像?
新课导入
上学期学习过比的认识时,我们讨论过图片像不像的问题,现在请同学们联系比的知识,再想一想,怎样的两张图片最像,怎样的图片不像?
2、图 A 与 图 D 最 像
1、图 A 与图 B 最 像
比相等的像,不相等的不像。D和A的长和长、宽和宽的比相等,12:6=8:4,所以就像。
看看淘气怎么说,你怎样认为?
√
淘气说的真对,我们同意他的说法
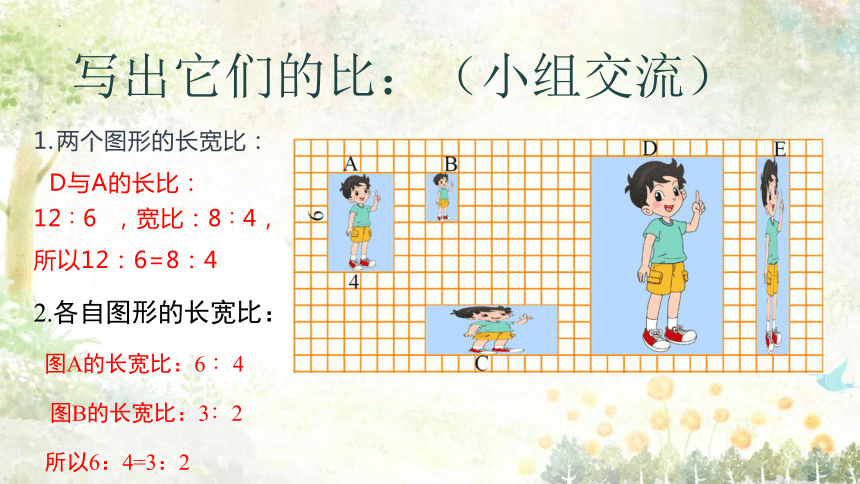
写出它们的比:(小组交流)
两个图形的长宽比:
D与A的长比: 12∶6 ,宽比:8∶4,
所以12:6=8:4
2.各自图形的长宽比:
图A的长宽比:6 ∶4
图B的长宽比:3∶2
所以6:4=3:2
我们来看看学校里的两面国旗的长和
宽的比值有什么关系。
长2.4m,宽1.6m。
长60cm,宽40cm。
操场上的国旗: 2.4 : 1.6 =
教室里的国旗: 60 : 40 =
2.4m
1.6m
40cm
60cm
2.4︰1.6
2.4 : 1.6 = 60 : 40 =
60︰40
=
=
或
表示两个比相等的式子叫做比例。
1.比例各项的认识
2.4 : 1.6=60 : 40
内项
外项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
哪几组的两个比可以组成比例?把组成的比例写出来。
可以 15:18=30:36
不可以
不可以
可以
小试身手
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
16 ︰ 2
32 ︰ 4
=
外项
内项
=
16×4
2×32
观察下面的比例 ,你有什么发现?
比 4︰6
比例 2︰3=4︰6
比和比例有什么区别?
﹋
﹋
﹋
﹋
﹋
﹋
由两个数组成,是一个式子,
表示两个数相除。
由四个数组成,是一个等式。
表示两个比相等的式子。
拓展提高
比 比例
意义 两个数相除又叫作这两个数的比。 比表示两个数相除的关系。 表示两个比相等的式子叫作比例。
比例表示两个比相等的关系,是一个等式。
项数和名称 由两项组成,分别叫作比的前项和后项 由四项组成,两端的两项叫作比例的外项,中间的两项叫作比例的内项。
基本性质 比的前项和后项同时乘或除以一个不为0的数,比值不变。比的基本性质用于化简比。 在比例里,两个内项的积等于两个外项的积。比例的基本性质用于解比例。
第一关: 填空乐园。
(1)a:8=6:b中,( )和( )是外项,( )和( )是内项,a×b=( )。
a
b
8
6
48
(2)一个比例的两个内项互为倒数,一个外项是 ,另一个外项是( )。
6
随堂演练
(3)在比例里,两个内项的积是18,
其中一个外项是2,另一个外项
是( )。
(4)如果5a=3b,那么, = ,
= 。
( )
( )
a
b
9
3
5
b
a
( )
( )
5
3
第二关 :火眼金睛
(1)( )与 3 : 5 能组成比例。
A. 10:6 B. : C. 30 : 50
(2) 4 : 5 与( ) 能组成比例。
A. : B. 8:10 C. 15 : 12
1
3
1
5
1
5
1
8
C
B
: = :
3
1
6
1
2
1
4
1
(1) : 和 :
(2) 1.2: 和 :5
可以组成比例
1.2×5=6
不能组成比例
第三关、知识应用
3
1
6
1
2
1
4
1
× =
3
1
4
1
12
1
× =
6
1
2
1
12
1
4
3
5
4
× =
4
3
5
4
5
3
1. 应用比例的意义或比例的基本性质,判断下面哪组中的两个比可以组成比例。
1.应用比例的基本性质判断下面的比例是否正确
(1)6:3 = 8:5
(2)0.2 : 2.5 = 4 :50
(3)2 :3 = :
(4)1.2 :0.6 = 10 :5
习题巩固
×
√
×
√
12:4 0.03:0.06
18:12 1
0.4:0.8 30:20
:
2、连一连。
下面的四个数可以组成比例吗?把组成的比例
写出来(能写几个写几个)。
2、3、4 和 6
因为 2 × 6 = 3 × 4 所以这四个数可以组成比例
2∶3 = 4∶6
2∶4 = 3∶6
6∶4 = 3∶2
6∶3 = 4∶2
4∶2 = 6∶3
4∶6 = 2∶3
3∶6 = 2∶4
3∶2 = 6∶4
比例的认识
1.在具体情境中,理解比例的意义和基本性质,会运用比例的意义和基本性质正确判断两个比能否组成比例。
2.在探索比例的意义和基本性质的过程中发展推理能力。
3.通过自主学习,经历探究的过程,体验成功的快乐。
学习目标
1、请同学们回忆一下,上学期我们学过的比的知识,谁能说说什么叫作比?
2、举例说明什么是比的前项、后项和比值。
3、化简下列各比。
16:4 25:5
4、求下面各比的比值。
: 0.81:0.9
复习回顾
全班交流:下面哪两张图片最像?
新课导入
上学期学习过比的认识时,我们讨论过图片像不像的问题,现在请同学们联系比的知识,再想一想,怎样的两张图片最像,怎样的图片不像?
2、图 A 与 图 D 最 像
1、图 A 与图 B 最 像
比相等的像,不相等的不像。D和A的长和长、宽和宽的比相等,12:6=8:4,所以就像。
看看淘气怎么说,你怎样认为?
√
淘气说的真对,我们同意他的说法
写出它们的比:(小组交流)
两个图形的长宽比:
D与A的长比: 12∶6 ,宽比:8∶4,
所以12:6=8:4
2.各自图形的长宽比:
图A的长宽比:6 ∶4
图B的长宽比:3∶2
所以6:4=3:2
我们来看看学校里的两面国旗的长和
宽的比值有什么关系。
长2.4m,宽1.6m。
长60cm,宽40cm。
操场上的国旗: 2.4 : 1.6 =
教室里的国旗: 60 : 40 =
2.4m
1.6m
40cm
60cm
2.4︰1.6
2.4 : 1.6 = 60 : 40 =
60︰40
=
=
或
表示两个比相等的式子叫做比例。
1.比例各项的认识
2.4 : 1.6=60 : 40
内项
外项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
哪几组的两个比可以组成比例?把组成的比例写出来。
可以 15:18=30:36
不可以
不可以
可以
小试身手
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
16 ︰ 2
32 ︰ 4
=
外项
内项
=
16×4
2×32
观察下面的比例 ,你有什么发现?
比 4︰6
比例 2︰3=4︰6
比和比例有什么区别?
﹋
﹋
﹋
﹋
﹋
﹋
由两个数组成,是一个式子,
表示两个数相除。
由四个数组成,是一个等式。
表示两个比相等的式子。
拓展提高
比 比例
意义 两个数相除又叫作这两个数的比。 比表示两个数相除的关系。 表示两个比相等的式子叫作比例。
比例表示两个比相等的关系,是一个等式。
项数和名称 由两项组成,分别叫作比的前项和后项 由四项组成,两端的两项叫作比例的外项,中间的两项叫作比例的内项。
基本性质 比的前项和后项同时乘或除以一个不为0的数,比值不变。比的基本性质用于化简比。 在比例里,两个内项的积等于两个外项的积。比例的基本性质用于解比例。
第一关: 填空乐园。
(1)a:8=6:b中,( )和( )是外项,( )和( )是内项,a×b=( )。
a
b
8
6
48
(2)一个比例的两个内项互为倒数,一个外项是 ,另一个外项是( )。
6
随堂演练
(3)在比例里,两个内项的积是18,
其中一个外项是2,另一个外项
是( )。
(4)如果5a=3b,那么, = ,
= 。
( )
( )
a
b
9
3
5
b
a
( )
( )
5
3
第二关 :火眼金睛
(1)( )与 3 : 5 能组成比例。
A. 10:6 B. : C. 30 : 50
(2) 4 : 5 与( ) 能组成比例。
A. : B. 8:10 C. 15 : 12
1
3
1
5
1
5
1
8
C
B
: = :
3
1
6
1
2
1
4
1
(1) : 和 :
(2) 1.2: 和 :5
可以组成比例
1.2×5=6
不能组成比例
第三关、知识应用
3
1
6
1
2
1
4
1
× =
3
1
4
1
12
1
× =
6
1
2
1
12
1
4
3
5
4
× =
4
3
5
4
5
3
1. 应用比例的意义或比例的基本性质,判断下面哪组中的两个比可以组成比例。
1.应用比例的基本性质判断下面的比例是否正确
(1)6:3 = 8:5
(2)0.2 : 2.5 = 4 :50
(3)2 :3 = :
(4)1.2 :0.6 = 10 :5
习题巩固
×
√
×
√
12:4 0.03:0.06
18:12 1
0.4:0.8 30:20
:
2、连一连。
下面的四个数可以组成比例吗?把组成的比例
写出来(能写几个写几个)。
2、3、4 和 6
因为 2 × 6 = 3 × 4 所以这四个数可以组成比例
2∶3 = 4∶6
2∶4 = 3∶6
6∶4 = 3∶2
6∶3 = 4∶2
4∶2 = 6∶3
4∶6 = 2∶3
3∶6 = 2∶4
3∶2 = 6∶4
