7.2.1离散型随机变量 课件(共28张PPT)
文档属性
| 名称 | 7.2.1离散型随机变量 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 05:19:10 | ||
图片预览








文档简介
(共28张PPT)
7.2.1离散型随机变量
人教A版2019必修第三册
一般地,一个试验如果满足下列条件:
①试验可以在相同的情形下重复进行;
②试验的所有可能结果是明确可知的,并且不只一个;
③每次试验总是恰好出现这些可能结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果;
这种试验就是一个随机试验,为了方便起见,也简称试验.
1.随机试验的概念
我们把随机试验E的每个可能的基本结果称为样本点,全体样本点的集合称为试验E的样本空间. 我们用Ω表示样本空间,用ω表示样本点.
2.样本点与样本空间的概念
求随机事件的概率时,我们往往需要为随机试验建立样本空间,并会涉及样本点和随机事件的表示问题,类似函数在数集与数集之间建立对应关系,如果我们在随机试验的样本空间与实数集之间建立某种对应,将不仅可以为一些随机事件的表示带来方便,而且能更好地利用数学工具研究随机试验.
有些随机试验的样本点与数值有关系,我们可以直接与实数建立对应关系.
例如,掷一枚骰子,用实数m(m=1, 2, 3, 4, 5, 6)表示“掷出的点数为m”; 又如,掷两枚骰子,样本空间为Ω={(x, y)|x, y=1, 2, , 6},用x+y表示“两枚骰子的点数之和”,样本点(x, y)就与实数x+y对应.
有些随机试验的样本点与数值没有直接关系,我们可以根据问题的需要为每个样本点指定一个数值.
例如,随机抽取一件产品,有“抽到次品”和“抽到正品”两种可能结果,它们与数值无关. 如果“抽到次品”用1表示,“抽到正品”用0表示,即定义
那么这个试验的样本点与实数就建立了对应关系.
类似地,掷一枚硬币,可将试验结果“正面朝上”用1表示,“反面朝上”用0表示;
随机调查学生的体育综合测试成绩,可将等级成绩优、良、中等、及格、不及格分别赋值5, 4, 3, 2, 1;等等.
对于任何一个随机试验,总可以把它的每个样本点与一个实数对应. 即通过引人一个取值依赖于样本点的变量X,来刻画样本点和实数的对应关系,实现样本点的数量化. 因为在随机试验中样本点的出现具有随机性,所以变量X的取值也具有随机性.
考察下列随机试验及其引入的变量:
试验1:从 100 个电子元件(至少含 3 个以上次品)中随机抽取三个进行检验,变量 X 表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量 Y 表示需要的抛掷次数.
这两个随机试验的样本空间各是什么?各个样本点与变量的值是如何对应的?变量 X,Y 有哪些共同的特征?
探究
探究新知
试验1: 从100个电子元件(至少含3个以上次品)中随机抽取三个进行检验,变量X表示三个元件中的次品数;
这两个随机试验的样本空间各是什么 各个样本点与变量的值是如何对应的 变量X, Y有哪些共同的特征
对于试验1,如果用0表示“元件为合格品”,1表示“元件为次品”,用0和1组成长度为3的字符串表示样本点,则样本空间Ω1={000, 001, 010, 011, 100, 101, 110, 111}. 各样本点与变量X的值的对应关系如下图所示.
试验2: 抛掷一枚硬币直到出现正面为止,变量Y表示需要的拋掷次数.
这两个随机试验的样本空间各是什么 各个样本点与变量的值是如何对应的 变量X, Y有哪些共同的特征
对于试验2,如果用h表示“正面朝上”,t表示“反面朝上”,例如用tth表示第3次才出现“正面朝上”,则样本空间Ω2={h, th, tth, tth, }. Ω2包含无穷多个样本点. 各样本点与变量Y的值的对应关系如下图所示.
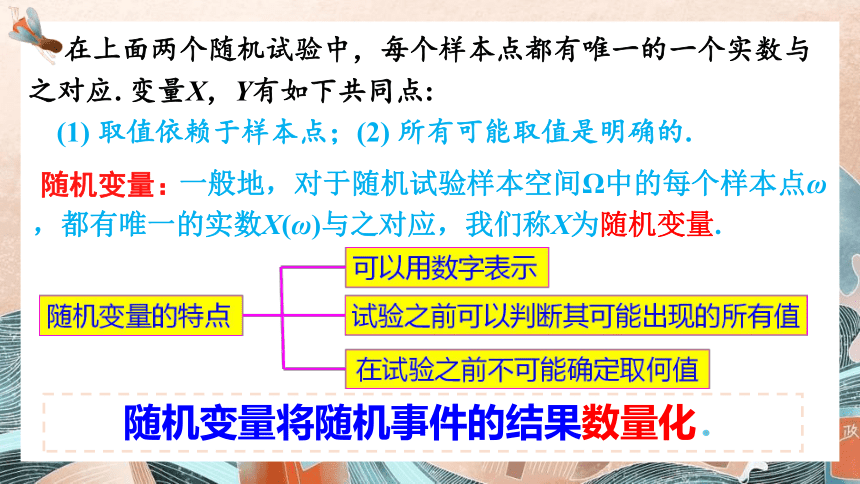
一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯一的实数X(ω)与之对应,我们称X为随机变量.
在上面两个随机试验中,每个样本点都有唯一的一个实数与之对应. 变量X,Y有如下共同点:
(1) 取值依赖于样本点;(2) 所有可能取值是明确的.
随机变量:
随机变量将随机事件的结果数量化.
试验1中随机变量X的可能取值为0, 1, 2, 3, 共有4个值;试验2中随机变量Y的可能取值为1, 2, 3, , 有无限个取值,但可以一一列举出来.
离散型随机变量的定义:
典例分析
下列变量中,哪些是随机变量,哪些不是随机变量?并说明理由.
(1)上海国际机场候机室中2018年10月1日的旅客数量;
(2)2019年某天济南至北京的D36次列车到北京站的时间;
(3)2019年5月1日到10月1日期间所查酒驾的人数;
(4)体积为1000 cm3的球的半径长.
随机变量
随机变量
随机变量
不是随机变量
连续型随机变量
连续型随机变量是指可以取某一区间的一切值的随机变量,又称作连续型随机变量。
现实生活中还有大量不是离散型随机变量的例子.例如,种子含水量的测量误差 X1;某品牌电视机的使用寿命 X2;测量某一个零件的长度产生的测量误差 X3.这些都是可能取值充满了某个区间、不能一一列举的随机变量.本节我们只研究取有限个值的离散型随机变量.
1.写出下列各随机变量可能的取值,并说明随机变量所取值所表示的随机试验的结果:
(1)从10张已编号的卡片(从1号到10号)中任取1张,被取出的卡片的号数X;
(2)一个袋中装有5个白球和5个黑球,从中任取3个,其中所含白球数X;
(3)抛掷两个骰子,所得点数之和X;
(4)接连不断地射击,首次命中目标需要的射击次数X;
(5)某一自动装置无故障运转的时间X;
(6)某林场树木最高达30米,此林场树木的高度X.
X=1, 2, 3, ···, n, ···
X=2, 3, 4, ···, 12
X取(0, +∞)内的一切值
X取(0, 30]内的一切值
X =1, 2, 3, ···, 10
X=0, 1, 2, 3
离散型
连续型
小试牛刀
随着试验结果变化而变化的变量称为随机变量,常用大写英文字母X,Y,Z…表示。
1、随机变量定义
2、随机变量的分类
①离散型随机变量:
X的取值可一、一列出
②连续型随机变量:
X可以取某个区间内的一切值
课堂小结
3、随机变量与函数的关系
(1)相同点
(2)不相同点
课堂练习(课本P60)
解:
2. 下列随机试验的结果能否用离散型随机变量表示 若能,请写出各随机变量可能的取值,并说明这些值所表示的随机试验的结果.
(1) 抛掷2枚骰子,所得点数之和;
(2) 某足球队在5次点球中射进的球数;
(3) 任意抽取一瓶标有1 500 ml的饮料,其实际含量与规定含量之差.
(1) 点数之和X是离散型随机变量,X的可能取值为2,3, ,12.
{X=k}表示掷出的点数之和为k.
(2) 进球个数Y是离散型随机变量,Y的可能取值为0,1,2,3,4,5.
{Y=k}表示射进k个球.
(3) 误差Z不是离散型随机变量.
THANKS
“
”
创新设计习题讲解
题型三 用随机变量表示事件的结果
例3 一个袋中装有5个白球和5个黑球,从中任取3个球,其中所含白球的个数为X.
(1)写出随机变量X的取值,并说明取值表示的试验结果;
解 X的所有可能的取值为0,1,2,3.
“X=0”表示取出3个黑球;
“X=1”表示取出1个白球2个黑球;
“X=2”表示取出2个白球1个黑球;
“X=3”表示取出3个白球.
(2)若规定取3个球,每取到一个白球加5分,取到黑球不加分,且最后不管结果如何都加上6分,求最终得分Y的可能取值,并判定Y的随机变量类型.
解 由题意可得Y=5X+6,而X可能的取值0,1,2,3,
所以Y对应的各值是6,11,16,21,
故Y的可能取值为6,11,16,21,
显然Y为离散型随机变量.
训练3 甲、乙两队员进行乒乓球单打比赛,规定采用“七局四胜制”,用X表示需要比赛的局数,写出X所有可能的取值,并写出表示的试验结果.
解 根据题意可知X的可能取值为4,5,6,7.
X=4表示共打了4局,甲、乙两人有1人连胜4局;
X=5表示在前4局中有1人输了一局,最后一局此人胜出;
X=6表示在前5局中有1人输了2局,最后一局此人胜出;
X=7表示在前6局中,两人打平,后一局有1人胜出.
创新设计习题讲解
——分层精练
2.一串钥匙有6把,只有一把能打开锁,依次试验,打不开的扔掉,直到找到能开锁的钥匙为止,则试验次数X的最大可能取值为( )
A.6 B.5
C.4 D.2
B
解析 由于是逐次试验,可能前5次都打不开锁,但是最后一把钥匙一定能打开锁.
11.一用户在打电话时忘了号码的最后四位数字,只记得最后四位数字两两不同,且都大于5,于是他随机拨最后四位数字(两两不同),设他拨到所要号码时已拨的次数为ξ,则随机变量ξ的所有可能取值的种数为( )
A
A.24 B.20
C.4 D.18
13.在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x,y,记ξ=|x-2|+|y-x|.写出ξ可能的取值,并说明ξ所表示的随机试验的结果.
解 因为x,y可能取的值为1,2,3,
所以0≤|x-2|≤1,0≤|x-y|≤2,
所以0≤ξ≤3,
所以ξ可能的取值为0,1,2,3.
用(x,y)表示第一次抽到卡片号码为x,第二次抽得卡片号码为y,则随机变量ξ取各值的意义为:
ξ=0表示两次抽到卡片编号都是2,即(2,2);
ξ=1表示(1,1),(2,1),(2,3),(3,3);
ξ=2表示(1,2),(3,2).
ξ=3表示(1,3),(3,1).
14.某次演唱比赛,需要加试文化科学素质,每位参赛选手需回答3个问题,组委会为每位选手都备有10道不同的题目可供选择,其中有5道文史类题目,3道科技类题目,2道体育类题目,测试时,每位选手从给定的10道题目中不放回地随机抽取3次,每次抽取一道题目,回答完该题后,再抽取下一道题目做答.某选手抽到科技类题目的道数为X.
(1)试求出随机变量X的可能取值;
(2){X=1}表示的试验结果是什么?可能出现多少种不同的结果?
解 (1)由题意得X的可能取值为0,1,2,3.
(2){X=1}表示的事件是“恰抽到一道科技类题目”.
创新设计习题讲解
——每日一刻钟
2.某人进行射击,共有5发子弹,击中目标或子弹打完就停止射击,设射击次数为ξ,则“ξ=5”表示的试验结果是( )
A.第5次击中目标 B.第5次未击中目标
C.前4次未击中目标 D.第4次击中目标
解析 击中目标或子弹打完就停止射击,射击次数为ξ=5,说明前4次均未击中目标.
C
7.2.1离散型随机变量
人教A版2019必修第三册
一般地,一个试验如果满足下列条件:
①试验可以在相同的情形下重复进行;
②试验的所有可能结果是明确可知的,并且不只一个;
③每次试验总是恰好出现这些可能结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果;
这种试验就是一个随机试验,为了方便起见,也简称试验.
1.随机试验的概念
我们把随机试验E的每个可能的基本结果称为样本点,全体样本点的集合称为试验E的样本空间. 我们用Ω表示样本空间,用ω表示样本点.
2.样本点与样本空间的概念
求随机事件的概率时,我们往往需要为随机试验建立样本空间,并会涉及样本点和随机事件的表示问题,类似函数在数集与数集之间建立对应关系,如果我们在随机试验的样本空间与实数集之间建立某种对应,将不仅可以为一些随机事件的表示带来方便,而且能更好地利用数学工具研究随机试验.
有些随机试验的样本点与数值有关系,我们可以直接与实数建立对应关系.
例如,掷一枚骰子,用实数m(m=1, 2, 3, 4, 5, 6)表示“掷出的点数为m”; 又如,掷两枚骰子,样本空间为Ω={(x, y)|x, y=1, 2, , 6},用x+y表示“两枚骰子的点数之和”,样本点(x, y)就与实数x+y对应.
有些随机试验的样本点与数值没有直接关系,我们可以根据问题的需要为每个样本点指定一个数值.
例如,随机抽取一件产品,有“抽到次品”和“抽到正品”两种可能结果,它们与数值无关. 如果“抽到次品”用1表示,“抽到正品”用0表示,即定义
那么这个试验的样本点与实数就建立了对应关系.
类似地,掷一枚硬币,可将试验结果“正面朝上”用1表示,“反面朝上”用0表示;
随机调查学生的体育综合测试成绩,可将等级成绩优、良、中等、及格、不及格分别赋值5, 4, 3, 2, 1;等等.
对于任何一个随机试验,总可以把它的每个样本点与一个实数对应. 即通过引人一个取值依赖于样本点的变量X,来刻画样本点和实数的对应关系,实现样本点的数量化. 因为在随机试验中样本点的出现具有随机性,所以变量X的取值也具有随机性.
考察下列随机试验及其引入的变量:
试验1:从 100 个电子元件(至少含 3 个以上次品)中随机抽取三个进行检验,变量 X 表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量 Y 表示需要的抛掷次数.
这两个随机试验的样本空间各是什么?各个样本点与变量的值是如何对应的?变量 X,Y 有哪些共同的特征?
探究
探究新知
试验1: 从100个电子元件(至少含3个以上次品)中随机抽取三个进行检验,变量X表示三个元件中的次品数;
这两个随机试验的样本空间各是什么 各个样本点与变量的值是如何对应的 变量X, Y有哪些共同的特征
对于试验1,如果用0表示“元件为合格品”,1表示“元件为次品”,用0和1组成长度为3的字符串表示样本点,则样本空间Ω1={000, 001, 010, 011, 100, 101, 110, 111}. 各样本点与变量X的值的对应关系如下图所示.
试验2: 抛掷一枚硬币直到出现正面为止,变量Y表示需要的拋掷次数.
这两个随机试验的样本空间各是什么 各个样本点与变量的值是如何对应的 变量X, Y有哪些共同的特征
对于试验2,如果用h表示“正面朝上”,t表示“反面朝上”,例如用tth表示第3次才出现“正面朝上”,则样本空间Ω2={h, th, tth, tth, }. Ω2包含无穷多个样本点. 各样本点与变量Y的值的对应关系如下图所示.
一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯一的实数X(ω)与之对应,我们称X为随机变量.
在上面两个随机试验中,每个样本点都有唯一的一个实数与之对应. 变量X,Y有如下共同点:
(1) 取值依赖于样本点;(2) 所有可能取值是明确的.
随机变量:
随机变量将随机事件的结果数量化.
试验1中随机变量X的可能取值为0, 1, 2, 3, 共有4个值;试验2中随机变量Y的可能取值为1, 2, 3, , 有无限个取值,但可以一一列举出来.
离散型随机变量的定义:
典例分析
下列变量中,哪些是随机变量,哪些不是随机变量?并说明理由.
(1)上海国际机场候机室中2018年10月1日的旅客数量;
(2)2019年某天济南至北京的D36次列车到北京站的时间;
(3)2019年5月1日到10月1日期间所查酒驾的人数;
(4)体积为1000 cm3的球的半径长.
随机变量
随机变量
随机变量
不是随机变量
连续型随机变量
连续型随机变量是指可以取某一区间的一切值的随机变量,又称作连续型随机变量。
现实生活中还有大量不是离散型随机变量的例子.例如,种子含水量的测量误差 X1;某品牌电视机的使用寿命 X2;测量某一个零件的长度产生的测量误差 X3.这些都是可能取值充满了某个区间、不能一一列举的随机变量.本节我们只研究取有限个值的离散型随机变量.
1.写出下列各随机变量可能的取值,并说明随机变量所取值所表示的随机试验的结果:
(1)从10张已编号的卡片(从1号到10号)中任取1张,被取出的卡片的号数X;
(2)一个袋中装有5个白球和5个黑球,从中任取3个,其中所含白球数X;
(3)抛掷两个骰子,所得点数之和X;
(4)接连不断地射击,首次命中目标需要的射击次数X;
(5)某一自动装置无故障运转的时间X;
(6)某林场树木最高达30米,此林场树木的高度X.
X=1, 2, 3, ···, n, ···
X=2, 3, 4, ···, 12
X取(0, +∞)内的一切值
X取(0, 30]内的一切值
X =1, 2, 3, ···, 10
X=0, 1, 2, 3
离散型
连续型
小试牛刀
随着试验结果变化而变化的变量称为随机变量,常用大写英文字母X,Y,Z…表示。
1、随机变量定义
2、随机变量的分类
①离散型随机变量:
X的取值可一、一列出
②连续型随机变量:
X可以取某个区间内的一切值
课堂小结
3、随机变量与函数的关系
(1)相同点
(2)不相同点
课堂练习(课本P60)
解:
2. 下列随机试验的结果能否用离散型随机变量表示 若能,请写出各随机变量可能的取值,并说明这些值所表示的随机试验的结果.
(1) 抛掷2枚骰子,所得点数之和;
(2) 某足球队在5次点球中射进的球数;
(3) 任意抽取一瓶标有1 500 ml的饮料,其实际含量与规定含量之差.
(1) 点数之和X是离散型随机变量,X的可能取值为2,3, ,12.
{X=k}表示掷出的点数之和为k.
(2) 进球个数Y是离散型随机变量,Y的可能取值为0,1,2,3,4,5.
{Y=k}表示射进k个球.
(3) 误差Z不是离散型随机变量.
THANKS
“
”
创新设计习题讲解
题型三 用随机变量表示事件的结果
例3 一个袋中装有5个白球和5个黑球,从中任取3个球,其中所含白球的个数为X.
(1)写出随机变量X的取值,并说明取值表示的试验结果;
解 X的所有可能的取值为0,1,2,3.
“X=0”表示取出3个黑球;
“X=1”表示取出1个白球2个黑球;
“X=2”表示取出2个白球1个黑球;
“X=3”表示取出3个白球.
(2)若规定取3个球,每取到一个白球加5分,取到黑球不加分,且最后不管结果如何都加上6分,求最终得分Y的可能取值,并判定Y的随机变量类型.
解 由题意可得Y=5X+6,而X可能的取值0,1,2,3,
所以Y对应的各值是6,11,16,21,
故Y的可能取值为6,11,16,21,
显然Y为离散型随机变量.
训练3 甲、乙两队员进行乒乓球单打比赛,规定采用“七局四胜制”,用X表示需要比赛的局数,写出X所有可能的取值,并写出表示的试验结果.
解 根据题意可知X的可能取值为4,5,6,7.
X=4表示共打了4局,甲、乙两人有1人连胜4局;
X=5表示在前4局中有1人输了一局,最后一局此人胜出;
X=6表示在前5局中有1人输了2局,最后一局此人胜出;
X=7表示在前6局中,两人打平,后一局有1人胜出.
创新设计习题讲解
——分层精练
2.一串钥匙有6把,只有一把能打开锁,依次试验,打不开的扔掉,直到找到能开锁的钥匙为止,则试验次数X的最大可能取值为( )
A.6 B.5
C.4 D.2
B
解析 由于是逐次试验,可能前5次都打不开锁,但是最后一把钥匙一定能打开锁.
11.一用户在打电话时忘了号码的最后四位数字,只记得最后四位数字两两不同,且都大于5,于是他随机拨最后四位数字(两两不同),设他拨到所要号码时已拨的次数为ξ,则随机变量ξ的所有可能取值的种数为( )
A
A.24 B.20
C.4 D.18
13.在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x,y,记ξ=|x-2|+|y-x|.写出ξ可能的取值,并说明ξ所表示的随机试验的结果.
解 因为x,y可能取的值为1,2,3,
所以0≤|x-2|≤1,0≤|x-y|≤2,
所以0≤ξ≤3,
所以ξ可能的取值为0,1,2,3.
用(x,y)表示第一次抽到卡片号码为x,第二次抽得卡片号码为y,则随机变量ξ取各值的意义为:
ξ=0表示两次抽到卡片编号都是2,即(2,2);
ξ=1表示(1,1),(2,1),(2,3),(3,3);
ξ=2表示(1,2),(3,2).
ξ=3表示(1,3),(3,1).
14.某次演唱比赛,需要加试文化科学素质,每位参赛选手需回答3个问题,组委会为每位选手都备有10道不同的题目可供选择,其中有5道文史类题目,3道科技类题目,2道体育类题目,测试时,每位选手从给定的10道题目中不放回地随机抽取3次,每次抽取一道题目,回答完该题后,再抽取下一道题目做答.某选手抽到科技类题目的道数为X.
(1)试求出随机变量X的可能取值;
(2){X=1}表示的试验结果是什么?可能出现多少种不同的结果?
解 (1)由题意得X的可能取值为0,1,2,3.
(2){X=1}表示的事件是“恰抽到一道科技类题目”.
创新设计习题讲解
——每日一刻钟
2.某人进行射击,共有5发子弹,击中目标或子弹打完就停止射击,设射击次数为ξ,则“ξ=5”表示的试验结果是( )
A.第5次击中目标 B.第5次未击中目标
C.前4次未击中目标 D.第4次击中目标
解析 击中目标或子弹打完就停止射击,射击次数为ξ=5,说明前4次均未击中目标.
C
