勾股定理的应用[上学期]
图片预览



文档简介
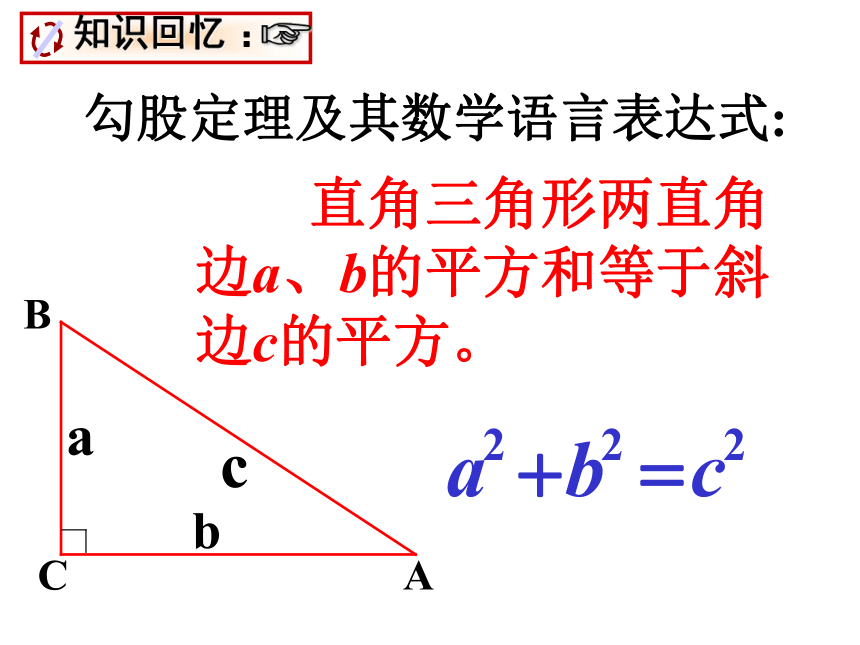
课件28张PPT。14.2 勾股定理应用勾股定理及其数学语言表达式: 直角三角形两直角边a、b的平方和等于斜边c的平方。CAB在△ABC中,∠C=90°.(1)若b=8,c=10,则a= ;(2)若a=5,b=10,则c = ;(3)若a=2,∠A=30° ,则 b = ;CAB611.23.5(2)、(3)两题结果精确到0.1 如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
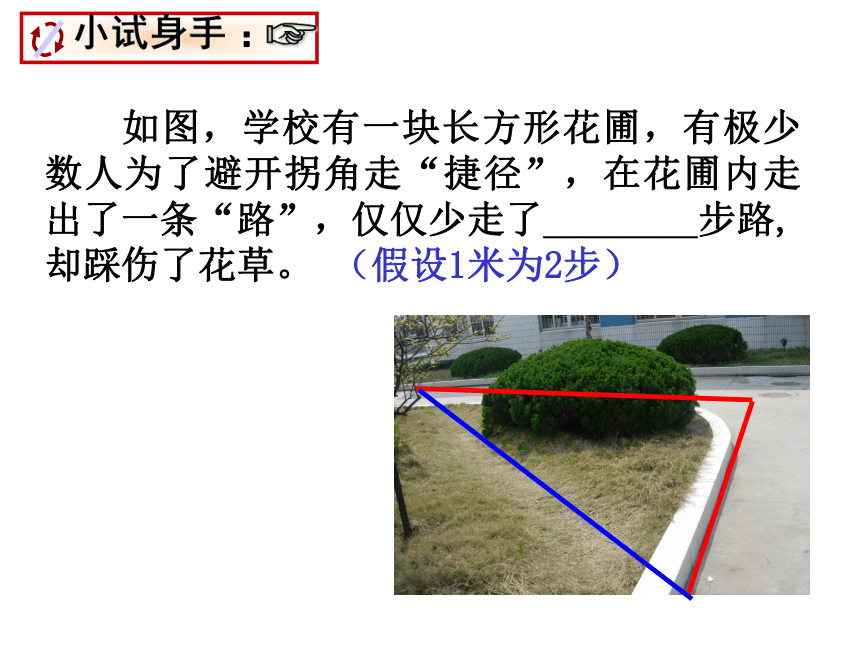
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
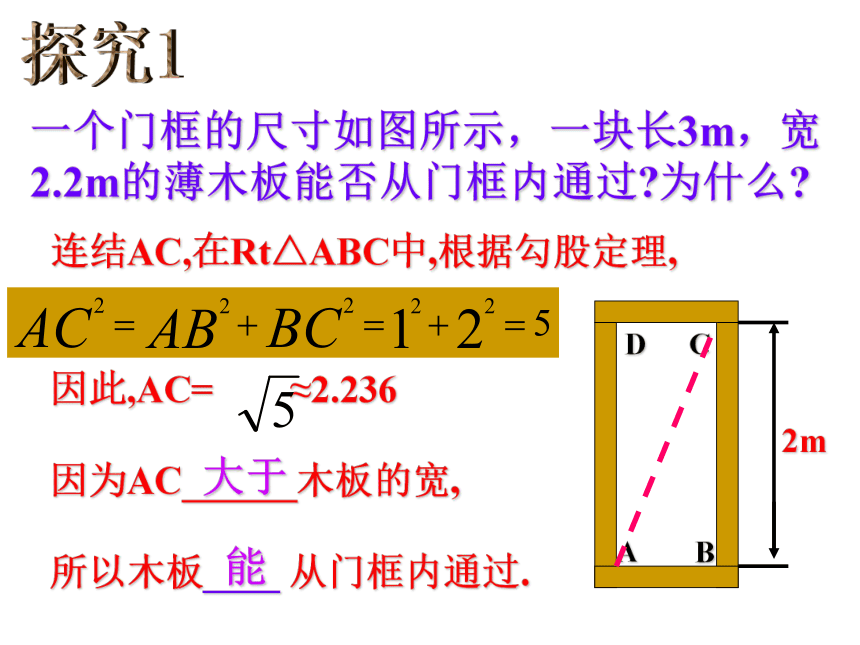
34“路”ABC5几何画板演示4探究1一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
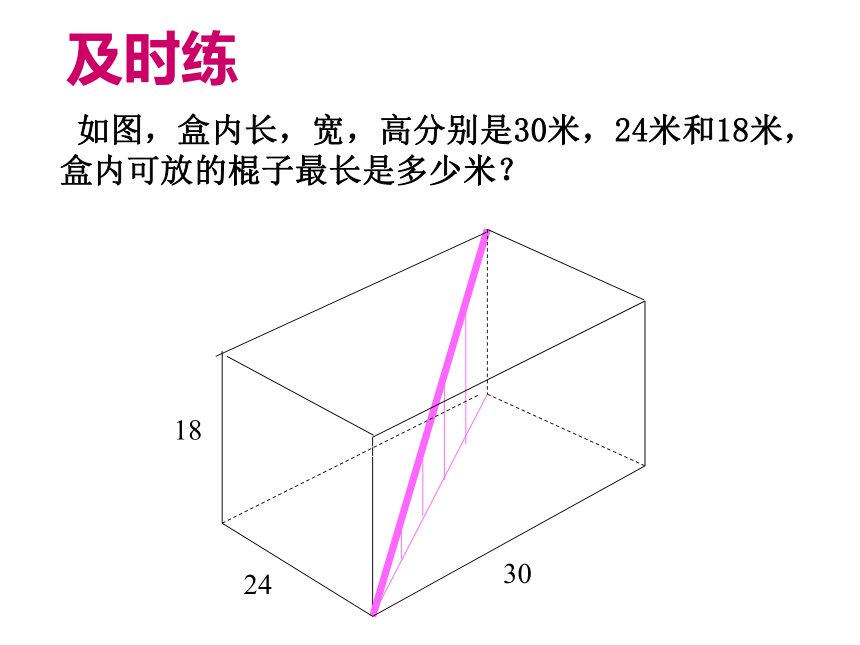
所以木板____ 从门框内通过.大于能 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?183024及时练一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?ACOBD探究 一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?探究2 ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?探究2 ACOBD 从题目和图形中,你能得到哪些信息?ACOBD分析:DB=OD-OB,求BD,可以 先求OB,OD.
在Rt△AOB中,梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m 如图,池塘边有两点A、B,无法直接测量AB之间的距离,请你运用所学过的知识设计一种方法,来测量AB间的距离。我来设计比一比,哪位同学的方法既多又好? 如图,池塘边有两
点A、B,点C是与BA
方向成直角的AC方向
上一点,现在测得
CB=60m,AC= 20m ,
请你求出A、B两点间
的距离。(结果保留整
数)我来算一算DABC名题鉴赏E 《九章算术》:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,请问这个水的深度与这根芦苇的长度各是多少?1如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8mBCA6m解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(-10不合,舍去)
答:梯子至少长10米。例1:
如图,求矩形零件上两孔中心A、B的距离.?小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米如图,在Rt△ABC中,BC=24,AC=7,求AB的长.在Rt△ABC中,根据勾股定理解:作如图所示上述解法正确吗?例2. 在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a﹕b=3﹕4,c=15.求a、b.分析:通过设未知数,根据勾股定理列出方程求
出a、b.解:设a=3x,b=4x
在Rt△ABC中,∠C=90°,
由勾股定理,得:a2+b2=c2
即:9x2+16x2=225
解得:x2=9 ∴x=3(负值舍去)
∴a=9, b=12.1、在一直角三角形中三边为a=3,b=4,则c= 。5或及时练2、在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a﹕c=3﹕5,b=20.则a=______c=___.
3、直角三角形一直角边长为6㎝,斜边为10㎝,则这个三角形的面积为_______,斜边上的高为_________ 思维拓展: 有没有一种直角三角形,已知一边可以求另外两边长呢?41.在Rt△ABC中,∠C=90 ,∠A=30 .则BC:AC:AB=
.
2.在Rt△ABC中,∠C=90 , AC=BC.则AC :BC :AB=
. 若AB=8则AC= .
又若CD⊥AB于D,则CD= .
12及时练 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD及时练 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=8及时练课时小结 谈谈你这节课的收获有哪些?会用勾股定理解决简单应用题;学会构造直角三角形.www.czsx.com.cn作业 见训案
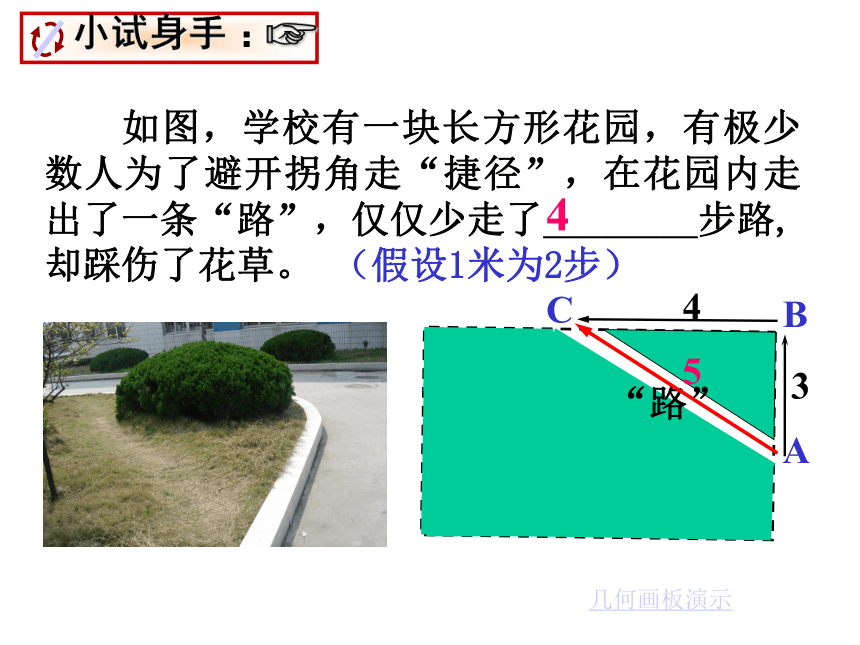
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
34“路”ABC5几何画板演示4探究1一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.大于能 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?183024及时练一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?ACOBD探究 一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?探究2 ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?探究2 ACOBD 从题目和图形中,你能得到哪些信息?ACOBD分析:DB=OD-OB,求BD,可以 先求OB,OD.
在Rt△AOB中,梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m 如图,池塘边有两点A、B,无法直接测量AB之间的距离,请你运用所学过的知识设计一种方法,来测量AB间的距离。我来设计比一比,哪位同学的方法既多又好? 如图,池塘边有两
点A、B,点C是与BA
方向成直角的AC方向
上一点,现在测得
CB=60m,AC= 20m ,
请你求出A、B两点间
的距离。(结果保留整
数)我来算一算DABC名题鉴赏E 《九章算术》:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,请问这个水的深度与这根芦苇的长度各是多少?1如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8mBCA6m解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(-10不合,舍去)
答:梯子至少长10米。例1:
如图,求矩形零件上两孔中心A、B的距离.?小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米如图,在Rt△ABC中,BC=24,AC=7,求AB的长.在Rt△ABC中,根据勾股定理解:作如图所示上述解法正确吗?例2. 在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a﹕b=3﹕4,c=15.求a、b.分析:通过设未知数,根据勾股定理列出方程求
出a、b.解:设a=3x,b=4x
在Rt△ABC中,∠C=90°,
由勾股定理,得:a2+b2=c2
即:9x2+16x2=225
解得:x2=9 ∴x=3(负值舍去)
∴a=9, b=12.1、在一直角三角形中三边为a=3,b=4,则c= 。5或及时练2、在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a﹕c=3﹕5,b=20.则a=______c=___.
3、直角三角形一直角边长为6㎝,斜边为10㎝,则这个三角形的面积为_______,斜边上的高为_________ 思维拓展: 有没有一种直角三角形,已知一边可以求另外两边长呢?41.在Rt△ABC中,∠C=90 ,∠A=30 .则BC:AC:AB=
.
2.在Rt△ABC中,∠C=90 , AC=BC.则AC :BC :AB=
. 若AB=8则AC= .
又若CD⊥AB于D,则CD= .
12及时练 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD及时练 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=8及时练课时小结 谈谈你这节课的收获有哪些?会用勾股定理解决简单应用题;学会构造直角三角形.www.czsx.com.cn作业 见训案
