人教版九年级上册25.2.1用列表法求概率(第2课时)课件(共20张PPT)
文档属性
| 名称 | 人教版九年级上册25.2.1用列表法求概率(第2课时)课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 14:44:52 | ||
图片预览








文档简介
(共20张PPT)
用列表法求概率
第二十五章 概率初步
复习回顾:
一般地,如果在一次试验中,
有n种可能的结果,并且它们发生的可能性都相等,
事件A包含在其中的m种结果,
那么事件A发生的概率为:
求概率的步骤:
(1)列举出一次试验中的所有结果(n个);
(2)找出其中事件A发生的结果(m个);
(3)运用公式求事件A的概率:
列举法:
就是把要数的对象一一列举出来分析求解的方法.
引例:掷两枚硬币,求下列事件的概率:
(1)两枚硬币全部正面朝上;
(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上;
“掷两枚硬币”共有几种结果?
正正
正反
反正
反反
为了不重不漏地列出所有这些结果,
你有什么好办法么?
掷两枚硬币,不妨设其中一枚为A,另一枚为B,
用列表法列举所有可能出现的结果:
B
A
正
反
正
反
正正
正反
反正
反反
共4种可能的结果
当一次试验涉及两个因素时,且可能出现的结果较多时,为不重复不遗漏地列出所有可能的结果,通常用列表法
这个游戏对小亮和小明公平吗?怎样才算公平
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:”我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜”。如果你是小亮,你愿意接受这个游戏的规则吗
思考1:
你能求出小亮得分的概率吗
1 2 3 4 5 6
1
2
3
4
5
6
红桃
黑桃
用表格表示
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
总结经验:
当一次试验要涉及两个因素,并且可能出
现的结果数目较多时,为了不重不漏的列
出所有可能的结果,通常采用列表的办法
解:由表中可以看出,在两堆牌中分别取一张,它可
能出现的结果有36个,它们出现的可能性相等
但满足两张牌的数字之积为奇数(记为事件A)
的有(1,1)(1,3)(1,5)(3,1)(3,3)(3,5)(5,1)(5,3)(5,5)
这9种情况,所以
P(A)=
这个游戏对小亮不公平
甲
乙
1
2
3
4
5
6
7
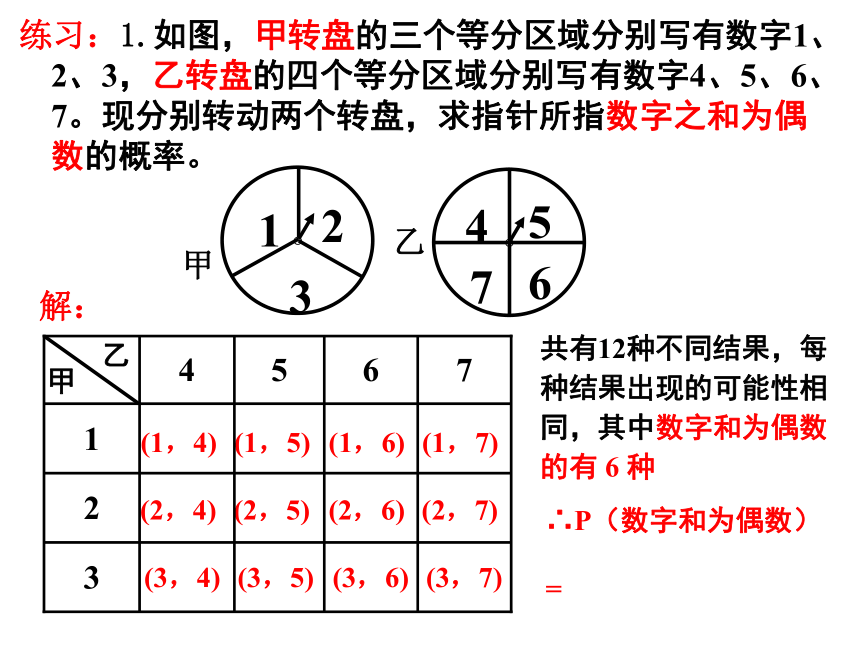
练习:1.如图,甲转盘的三个等分区域分别写有数字1、2、3,乙转盘的四个等分区域分别写有数字4、5、6、7。现分别转动两个转盘,求指针所指数字之和为偶数的概率。
解:
(1,4)
(1,5)
(1,6)
(1,7)
(2,4)
(2,5)
(2,6)
(2,7)
(3,4)
(3,5)
(3,6)
(3,7)
共有12种不同结果,每种结果出现的可能性相同,其中数字和为偶数的有 6 种
∴P(数字和为偶数)
=
3
2
1
7
6
5
4
甲
乙
要“玩”出水平
“配紫色”游戏
0650号同学为元旦晚会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.
游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)游戏者获胜的概率是多少
红
白
黄
蓝
绿
A盘
B盘
(2)利用列表的方法表示游戏
所有可能出现的结果.
表格可以是:
“配紫色”游戏
游戏者获胜的概率是1/6.
第二个 转盘 第一个 转盘
黄
蓝
绿
红
(红,黄)
(红,蓝)
(红,绿)
白
(白,黄)
(白,蓝)
(白,绿)
(2006年湖北宜昌)点M(x,y)可以在数字-1,0,1,2中任意选取.
试求(1)点M在第二象限内的概率.
(2)点M不在直线y=-2x+3上的概率.
学科内综合
-1 0 1 2
-1 (-1,-1) (0,-1) (1,-1) (2,-1)
0 (-1,0) (0,0) (1,0) (2,0)
1 (-1,1) (0,1) (1,1) (2,1)
2 (-1,2) (0,2) (1,2) (2,2)
x
y
解:列表如下:
∴ (1)P(点M在第一象限)= =
1/4
4/16
(2)P(点M不在直线y=-2x+3上)= =
14/16
7/8
练习、2.同时掷两个质地相同的骰子,计算下列事件的概率:
(1)两个骰子的点数相同;(2)两个骰子的点数和是9;
(3)至少有个骰子的点数是2。
解:
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,5) (6,6)
二
一
此题用列树图的方法好吗?
P(点数相同)=
P(点数和是9)=
P(至少有个骰子的点数是2 )=
思考
“同时掷两个质地相同的骰子”与
“把一个骰子掷两次”,所得到的结果有变化吗?
“同时掷两个质地相同的骰子”
两个骰子各出现的点数为1~6点
“把一个骰子掷两次”
两次骰子各出现的点数仍为1~6点
归纳
“两个相同的随机事件同时发生”与
“一个随机事件先后两次发生”的结果是一样的。
随机事件“同时”与“先后”的关系:
3、甲、乙两人各掷一枚质量分布均匀的正方体骰子,如果点数
之积为奇数,那么甲得1分;如果点数之积为偶数,那么乙得1分。
连续投10次,谁得分高,谁就获胜。
(1)请你想一想,谁获胜的机会大?并说明理由;
(2)你认为游戏公平吗?如果不公平,请你设计一个公平的游戏。
1 2 3 4 5 6
1 1×1=1 2×1=2 3×1=3 4×1=4 5×1=5 6×1=6
2 1×2=2 2×2=4 3×2=6 4×2=8 5×2=10 6×2=12
3 1×3=3 2×3=6 3×3=9 4×3=12 5×3=15 6×3=18
4 1×4=4 2×4=8 3×4=12 4×4=16 5×4=20 6×4=24
5 1×5=5 2×5=10 3×5=15 4×5=20 5×5=25 6×5=30
6 1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36
列出所有可能的结果:
(2006年山西大同)已知电流在一定时间段内正常通过电子元件
的概率是0.5,分别在一定时间段内,A、B之间和C、D之间电流能够正常通过的概率。
A B
(提示:在一次实验中,每个电子元件的状态有两个可能(通电、断开),并且这两种状态的可能性相等,用列举的方法可以得出电路的四种状态。)
C
D
4、在6张卡片上分别写有1~6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第二次取出的数字能够整除第一次取出的数字的概率是多少?
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
二
一
解: 列出所有可能的结果:
P(第二次取出的数字能够整除第一次取出的数字)=
随堂练习
(基础练习)
1、一个袋子中装有2个红球和2个绿球,任意摸出一球,记录颜色放回,再任意摸出一球,记录颜色放回,请你估计两次都摸到红球的概率是________。
2、某人有红、白、蓝三件衬衫和红、白、蓝三条长裤,该人任意拿一件衬衫和一条长裤,求正好是一套白色的概率_________。
3、在6张卡片上分别写有1—6的整数,随机的抽取一张后放回,再随机的抽取一张,那么,第一次取出的数字能够整除第2次取出的数字的概率是多少
2、染色体隐性遗传病,只有致病基因在纯合状态(dd)时才会发病,在杂合状态(Dd)时,由于正常的显性基因型D存在,致病基因d的作用不能表现出来,但是自己虽不发病,却能将病传给后代,常常父母无病,子女有病,如下表所示:
母亲基因型Dd
D d
父亲基因型Dd D DD Dd
d Dd dd
(1)子女发病的概率是多少?
(2)如果父亲基因型为Dd,母亲基因型为dd,问子女发病的概率是多少?
小结
1.“列表法”的意义
3.随机事件“同时”与“先后”的关系;
“放回”与“不放回”的关系.
2. 利用树图列举所有结果的方法.
用列表法求概率
第二十五章 概率初步
复习回顾:
一般地,如果在一次试验中,
有n种可能的结果,并且它们发生的可能性都相等,
事件A包含在其中的m种结果,
那么事件A发生的概率为:
求概率的步骤:
(1)列举出一次试验中的所有结果(n个);
(2)找出其中事件A发生的结果(m个);
(3)运用公式求事件A的概率:
列举法:
就是把要数的对象一一列举出来分析求解的方法.
引例:掷两枚硬币,求下列事件的概率:
(1)两枚硬币全部正面朝上;
(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上;
“掷两枚硬币”共有几种结果?
正正
正反
反正
反反
为了不重不漏地列出所有这些结果,
你有什么好办法么?
掷两枚硬币,不妨设其中一枚为A,另一枚为B,
用列表法列举所有可能出现的结果:
B
A
正
反
正
反
正正
正反
反正
反反
共4种可能的结果
当一次试验涉及两个因素时,且可能出现的结果较多时,为不重复不遗漏地列出所有可能的结果,通常用列表法
这个游戏对小亮和小明公平吗?怎样才算公平
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:”我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜”。如果你是小亮,你愿意接受这个游戏的规则吗
思考1:
你能求出小亮得分的概率吗
1 2 3 4 5 6
1
2
3
4
5
6
红桃
黑桃
用表格表示
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
总结经验:
当一次试验要涉及两个因素,并且可能出
现的结果数目较多时,为了不重不漏的列
出所有可能的结果,通常采用列表的办法
解:由表中可以看出,在两堆牌中分别取一张,它可
能出现的结果有36个,它们出现的可能性相等
但满足两张牌的数字之积为奇数(记为事件A)
的有(1,1)(1,3)(1,5)(3,1)(3,3)(3,5)(5,1)(5,3)(5,5)
这9种情况,所以
P(A)=
这个游戏对小亮不公平
甲
乙
1
2
3
4
5
6
7
练习:1.如图,甲转盘的三个等分区域分别写有数字1、2、3,乙转盘的四个等分区域分别写有数字4、5、6、7。现分别转动两个转盘,求指针所指数字之和为偶数的概率。
解:
(1,4)
(1,5)
(1,6)
(1,7)
(2,4)
(2,5)
(2,6)
(2,7)
(3,4)
(3,5)
(3,6)
(3,7)
共有12种不同结果,每种结果出现的可能性相同,其中数字和为偶数的有 6 种
∴P(数字和为偶数)
=
3
2
1
7
6
5
4
甲
乙
要“玩”出水平
“配紫色”游戏
0650号同学为元旦晚会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.
游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)游戏者获胜的概率是多少
红
白
黄
蓝
绿
A盘
B盘
(2)利用列表的方法表示游戏
所有可能出现的结果.
表格可以是:
“配紫色”游戏
游戏者获胜的概率是1/6.
第二个 转盘 第一个 转盘
黄
蓝
绿
红
(红,黄)
(红,蓝)
(红,绿)
白
(白,黄)
(白,蓝)
(白,绿)
(2006年湖北宜昌)点M(x,y)可以在数字-1,0,1,2中任意选取.
试求(1)点M在第二象限内的概率.
(2)点M不在直线y=-2x+3上的概率.
学科内综合
-1 0 1 2
-1 (-1,-1) (0,-1) (1,-1) (2,-1)
0 (-1,0) (0,0) (1,0) (2,0)
1 (-1,1) (0,1) (1,1) (2,1)
2 (-1,2) (0,2) (1,2) (2,2)
x
y
解:列表如下:
∴ (1)P(点M在第一象限)= =
1/4
4/16
(2)P(点M不在直线y=-2x+3上)= =
14/16
7/8
练习、2.同时掷两个质地相同的骰子,计算下列事件的概率:
(1)两个骰子的点数相同;(2)两个骰子的点数和是9;
(3)至少有个骰子的点数是2。
解:
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,5) (6,6)
二
一
此题用列树图的方法好吗?
P(点数相同)=
P(点数和是9)=
P(至少有个骰子的点数是2 )=
思考
“同时掷两个质地相同的骰子”与
“把一个骰子掷两次”,所得到的结果有变化吗?
“同时掷两个质地相同的骰子”
两个骰子各出现的点数为1~6点
“把一个骰子掷两次”
两次骰子各出现的点数仍为1~6点
归纳
“两个相同的随机事件同时发生”与
“一个随机事件先后两次发生”的结果是一样的。
随机事件“同时”与“先后”的关系:
3、甲、乙两人各掷一枚质量分布均匀的正方体骰子,如果点数
之积为奇数,那么甲得1分;如果点数之积为偶数,那么乙得1分。
连续投10次,谁得分高,谁就获胜。
(1)请你想一想,谁获胜的机会大?并说明理由;
(2)你认为游戏公平吗?如果不公平,请你设计一个公平的游戏。
1 2 3 4 5 6
1 1×1=1 2×1=2 3×1=3 4×1=4 5×1=5 6×1=6
2 1×2=2 2×2=4 3×2=6 4×2=8 5×2=10 6×2=12
3 1×3=3 2×3=6 3×3=9 4×3=12 5×3=15 6×3=18
4 1×4=4 2×4=8 3×4=12 4×4=16 5×4=20 6×4=24
5 1×5=5 2×5=10 3×5=15 4×5=20 5×5=25 6×5=30
6 1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36
列出所有可能的结果:
(2006年山西大同)已知电流在一定时间段内正常通过电子元件
的概率是0.5,分别在一定时间段内,A、B之间和C、D之间电流能够正常通过的概率。
A B
(提示:在一次实验中,每个电子元件的状态有两个可能(通电、断开),并且这两种状态的可能性相等,用列举的方法可以得出电路的四种状态。)
C
D
4、在6张卡片上分别写有1~6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第二次取出的数字能够整除第一次取出的数字的概率是多少?
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
二
一
解: 列出所有可能的结果:
P(第二次取出的数字能够整除第一次取出的数字)=
随堂练习
(基础练习)
1、一个袋子中装有2个红球和2个绿球,任意摸出一球,记录颜色放回,再任意摸出一球,记录颜色放回,请你估计两次都摸到红球的概率是________。
2、某人有红、白、蓝三件衬衫和红、白、蓝三条长裤,该人任意拿一件衬衫和一条长裤,求正好是一套白色的概率_________。
3、在6张卡片上分别写有1—6的整数,随机的抽取一张后放回,再随机的抽取一张,那么,第一次取出的数字能够整除第2次取出的数字的概率是多少
2、染色体隐性遗传病,只有致病基因在纯合状态(dd)时才会发病,在杂合状态(Dd)时,由于正常的显性基因型D存在,致病基因d的作用不能表现出来,但是自己虽不发病,却能将病传给后代,常常父母无病,子女有病,如下表所示:
母亲基因型Dd
D d
父亲基因型Dd D DD Dd
d Dd dd
(1)子女发病的概率是多少?
(2)如果父亲基因型为Dd,母亲基因型为dd,问子女发病的概率是多少?
小结
1.“列表法”的意义
3.随机事件“同时”与“先后”的关系;
“放回”与“不放回”的关系.
2. 利用树图列举所有结果的方法.
同课章节目录
