勾股定理复习课[上学期]
图片预览





文档简介
课件14张PPT。勾股定理的综合应用一、知识点聚焦如果直角三角形两直角边分别为a,b,斜边为c,
那么勾股定理a2 + b2 = c2直角三角形两直角边的平方和等于斜边的平方.即课前热身勾股定理的逆定理 如果三角形的三边长a,b,c满足a2 +b2=c2 ,
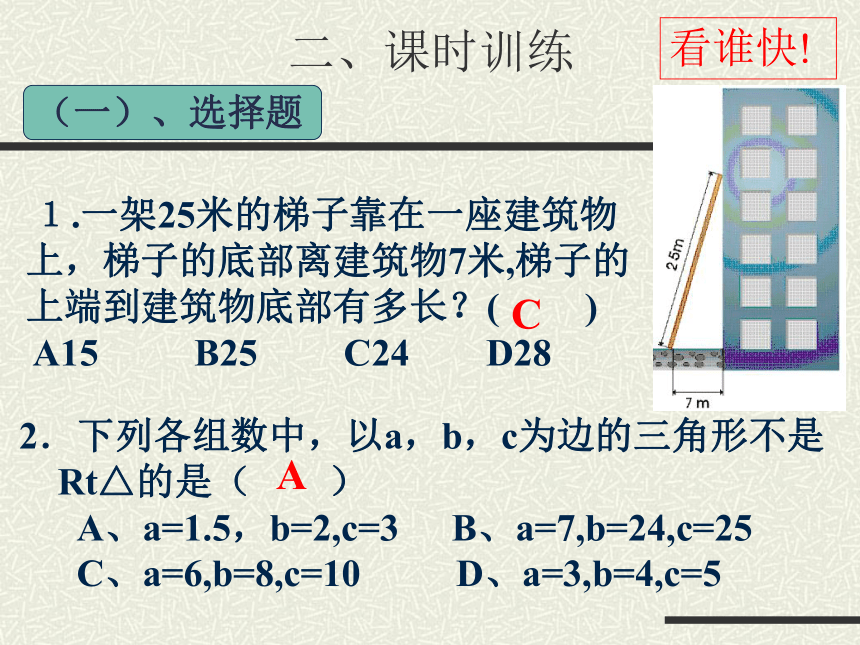
那么这个三角形是直角三角形直角三角形的判定从角的关系判定:课前热身(1)(2)两边互相垂直从边的关系判定:(一)、选择题看谁快!1.一架25米的梯子靠在一座建筑物上,梯子的底部离建筑物7米,梯子的上端到建筑物底部有多长?( )
A15 B25 C24 D282.下列各组数中,以a,b,c为边的三角形不是
Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6,b=8,c=10 D、a=3,b=4,c=5A二、课时训练C3.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm4.已知一个Rt△的两边长分别为3和4,则第三
三边长的平方是( )
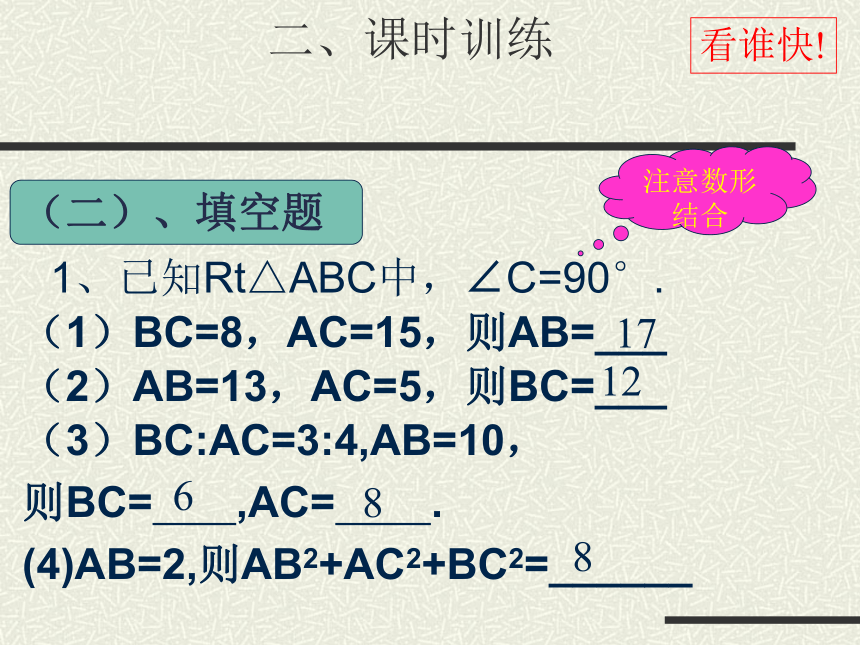
A、25 B、14 C、7 D、7或25D看谁细心!D二、课时训练(二)、填空题(1)BC=8,AC=15,则AB=___(2)AB=13,AC=5,则BC=___1、已知Rt△ABC中,∠C=90°.(3)BC:AC=3:4,AB=10,
则BC= ,AC= .
(4)AB=2,则AB2+AC2+BC2=______看谁快!1712688二、课时训练注意数形结合2 、(06佛山) 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形A、 B、 C、 D的面积和是______. 49cm2看谁厉害!二、课时训练已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°.综合例练(1)求BD的长;(2)试判定△BCD 的形状;(3)求四边形ABCD的面积;(4)求BC边上的高.解:连结BD
(1) 在Rt △ABD中, ∠A=90°,
AB=3cm,AD=4cm
则可得: BD2=AB2+AD2=32+42=25
∴BD=5cm(2) ∵BD2+CD2=52+122=169=BC2,
∴ △BCD是直角三角形(3) S四边形ACD=S △ABD+S △BCD
=? × 3 × 4+? × 5 × 12
=36(cm2)
根据什么定理?勾股定理勾股定理的逆定理谈一谈你的收获是…? 本节课主要是应用勾股定理和它的逆定理来解决实际问题,应注意:
1、数形结合;
2、勾股定理和它的逆定理的使用区别,不要用错定理。如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA小组比拼!思考题: 已知三角形三边长a b c, 满足(n>1) a=n2-1, b=2n, c=n2+1, 试判断三角形是否是直角三角形.若是,请指出其直角.思考题:解: ∵ a2=(n2-1)2=n4-2n2+1
b2=(2n)2=4n2
c2 =(n2+1)2=n4+2n2+1
∴ a2+b2=c2
根据勾
∴此三角形是直角三角形
c边所对的角是直角3、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度?DABC小组比拼!
那么勾股定理a2 + b2 = c2直角三角形两直角边的平方和等于斜边的平方.即课前热身勾股定理的逆定理 如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形直角三角形的判定从角的关系判定:课前热身(1)(2)两边互相垂直从边的关系判定:(一)、选择题看谁快!1.一架25米的梯子靠在一座建筑物上,梯子的底部离建筑物7米,梯子的上端到建筑物底部有多长?( )
A15 B25 C24 D282.下列各组数中,以a,b,c为边的三角形不是
Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6,b=8,c=10 D、a=3,b=4,c=5A二、课时训练C3.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm4.已知一个Rt△的两边长分别为3和4,则第三
三边长的平方是( )
A、25 B、14 C、7 D、7或25D看谁细心!D二、课时训练(二)、填空题(1)BC=8,AC=15,则AB=___(2)AB=13,AC=5,则BC=___1、已知Rt△ABC中,∠C=90°.(3)BC:AC=3:4,AB=10,
则BC= ,AC= .
(4)AB=2,则AB2+AC2+BC2=______看谁快!1712688二、课时训练注意数形结合2 、(06佛山) 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形A、 B、 C、 D的面积和是______. 49cm2看谁厉害!二、课时训练已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°.综合例练(1)求BD的长;(2)试判定△BCD 的形状;(3)求四边形ABCD的面积;(4)求BC边上的高.解:连结BD
(1) 在Rt △ABD中, ∠A=90°,
AB=3cm,AD=4cm
则可得: BD2=AB2+AD2=32+42=25
∴BD=5cm(2) ∵BD2+CD2=52+122=169=BC2,
∴ △BCD是直角三角形(3) S四边形ACD=S △ABD+S △BCD
=? × 3 × 4+? × 5 × 12
=36(cm2)
根据什么定理?勾股定理勾股定理的逆定理谈一谈你的收获是…? 本节课主要是应用勾股定理和它的逆定理来解决实际问题,应注意:
1、数形结合;
2、勾股定理和它的逆定理的使用区别,不要用错定理。如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA小组比拼!思考题: 已知三角形三边长a b c, 满足(n>1) a=n2-1, b=2n, c=n2+1, 试判断三角形是否是直角三角形.若是,请指出其直角.思考题:解: ∵ a2=(n2-1)2=n4-2n2+1
b2=(2n)2=4n2
c2 =(n2+1)2=n4+2n2+1
∴ a2+b2=c2
根据勾
∴此三角形是直角三角形
c边所对的角是直角3、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度?DABC小组比拼!
