第七章:平面直角坐标系练习题2021-2022学年甘肃省七年级下学期人教版数学期末试题选编(含解析)
文档属性
| 名称 | 第七章:平面直角坐标系练习题2021-2022学年甘肃省七年级下学期人教版数学期末试题选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 422.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 16:48:30 | ||
图片预览



文档简介
第七章:平面直角坐标系
一、单选题
1.(2022春·甘肃武威·七年级统考期末)若点在第二象限,则点在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2022春·甘肃陇南·七年级统考期末)如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )
A.(﹣1,2) B.(﹣9,6) C.(﹣1,6) D.(﹣9,2)
二、填空题
3.(2022春·甘肃武威·七年级统考期末)在平面直角坐标系中,点坐标为,若轴,且线段,则点坐标为__________.
4.(2022春·甘肃陇南·七年级统考期末)点在第三象限,距离轴个单位长度,距离轴个单位长度,则点的坐标为______.
5.(2022春·甘肃武威·七年级统考期末)在平面直角坐标系中,点P(2,﹣3)在__________象限.
6.(2022春·甘肃嘉峪关·七年级统考期末)若点M(a-3,a+4)在y轴上,则a=___________.
7.(2022春·甘肃陇南·七年级统考期末)已知点在轴上,则点的坐标为__________.
8.(2022春·甘肃武威·七年级统考期末)平面直角坐标系中,由点组成的的面积是______.
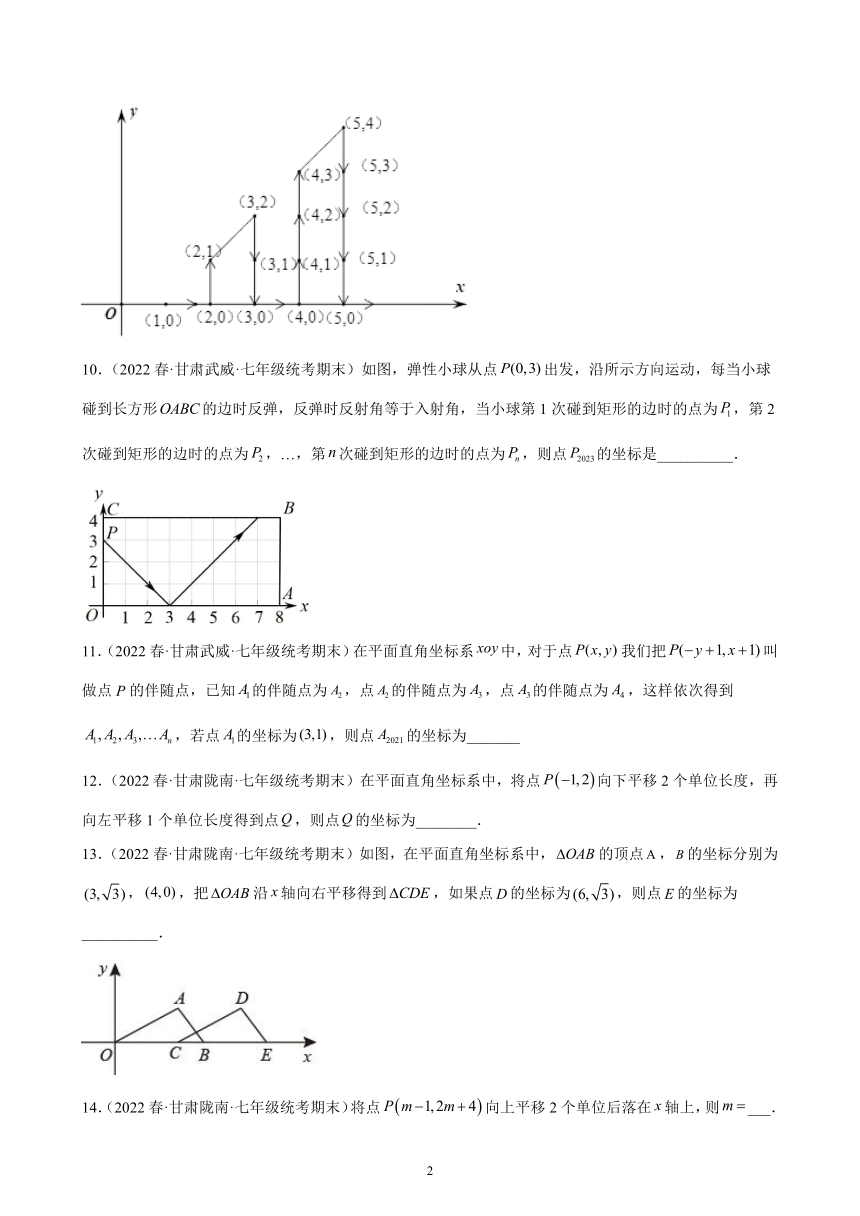
9.(2022春·甘肃陇南·七年级统考期末)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如,,,,,,根据这个规律探索可得,第个点的坐标为_____.
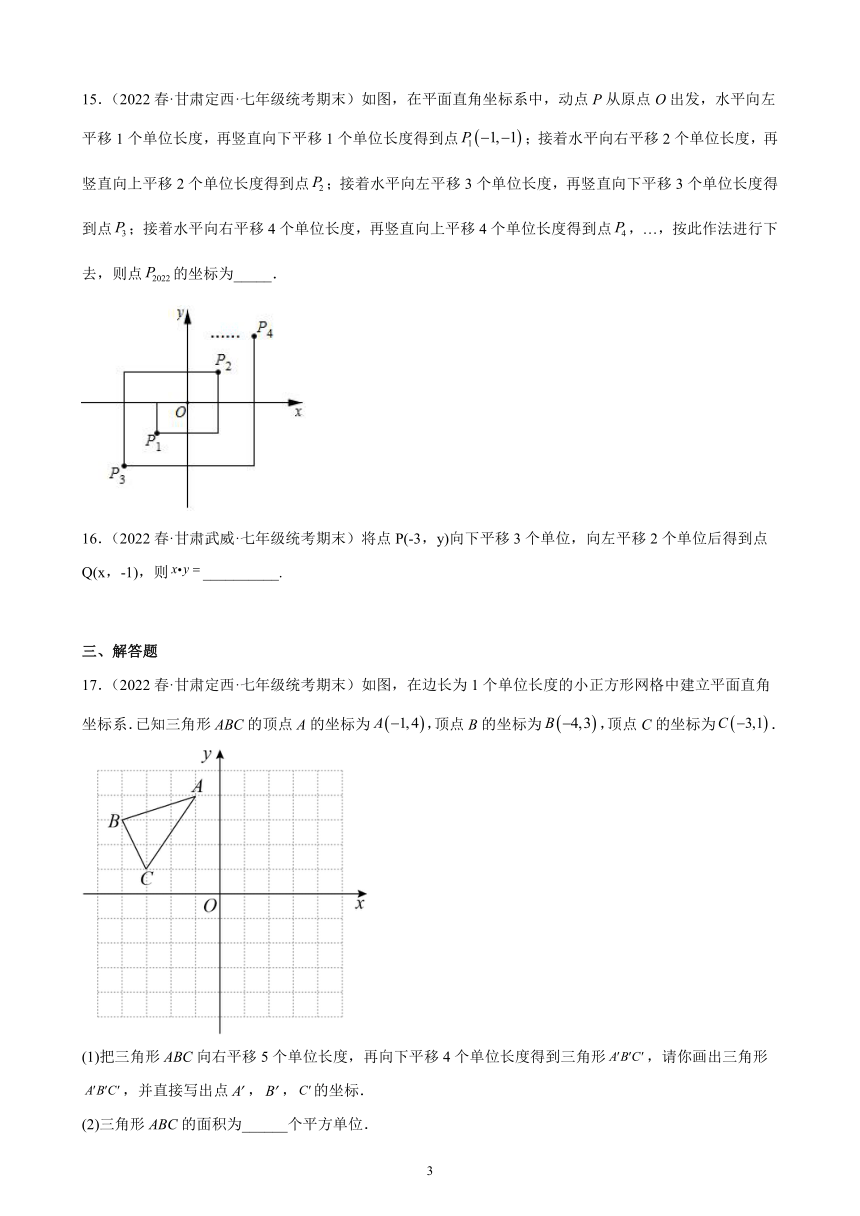
10.(2022春·甘肃武威·七年级统考期末)如图,弹性小球从点出发,沿所示方向运动,每当小球碰到长方形的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为,第2次碰到矩形的边时的点为,…,第次碰到矩形的边时的点为,则点的坐标是__________.
11.(2022春·甘肃武威·七年级统考期末)在平面直角坐标系中,对于点我们把叫做点P的伴随点,已知的伴随点为,点的伴随点为,点的伴随点为,这样依次得到,若点的坐标为,则点的坐标为_______
12.(2022春·甘肃陇南·七年级统考期末)在平面直角坐标系中,将点向下平移2个单位长度,再向左平移1个单位长度得到点,则点的坐标为________.
13.(2022春·甘肃陇南·七年级统考期末)如图,在平面直角坐标系中,的顶点,的坐标分别为,,把沿轴向右平移得到,如果点的坐标为,则点的坐标为__________.
14.(2022春·甘肃陇南·七年级统考期末)将点向上平移2个单位后落在轴上,则___.
15.(2022春·甘肃定西·七年级统考期末)如图,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点,…,按此作法进行下去,则点的坐标为_____.
16.(2022春·甘肃武威·七年级统考期末)将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则__________.
三、解答题
17.(2022春·甘肃定西·七年级统考期末)如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系.已知三角形ABC的顶点A的坐标为,顶点B的坐标为,顶点C的坐标为.
(1)把三角形ABC向右平移5个单位长度,再向下平移4个单位长度得到三角形,请你画出三角形,并直接写出点,,的坐标.
(2)三角形ABC的面积为______个平方单位.
18.(2022春·甘肃平凉·七年级统考期末)如图为某中学新校区分布图的一部分,方格纸中每个小方格都是边长为1个单位长度的正方形,若教学楼的坐标为,图书馆的坐标为,解答下列问题:
(1)在图中找到坐标系中的原点,并建立平面直角坐标系;
(2)若体育馆的坐标为,食堂的坐标为,请在图中标出体育馆和食堂的位置,并求出教学楼到体育馆的距离(1格=150米).
19.(2022春·甘肃武威·七年级统考期末)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(4,0),,C(5,-3),点A经过平移后对应点为A1(0,4),将△ABC作同样的平移得到△A1B1C1.
(1)若边上一点经过上述平移后的对应点为,用含,的式子表示点的坐标为________(直接写出结果即可).
(2)在图中画出平移后的△A1B1C1并写出B1、C1的坐标.
20.(2022春·甘肃陇南·七年级统考期末)如图,在边长为1个单位长度的小正方形组成的网格中,格点三角形(顶点为网格线的交点)的顶点,的坐标分别为,.
(1)请在网格图中建立平面直角坐标系;
(2)将先向左平移5个单位长度,再向下平移6个单位长度,请画出两次平移后的,并直接写出点的对应点的坐标;
(3)若是内一点,直接写出中的对应点的坐标.
参考答案:
1.C
【分析】根据第二象限内的点的横坐标小于零,纵坐标大于零,可得关于a、b的不等式,再根据不等式的性质,可得B点的坐标符号.
【详解】解:根据题意知,
解得:a<﹣1,b>2,
则a-3<0,1-b<0,
∴点在第三象限,
故选:C.
【点睛】本题考查了点的坐标,利用第二象限内点的横坐标小于零,纵坐标大于零得出不等式,又利用不等式的性质得出B点的坐标符号是解题关键.
2.A
【分析】根据平移规律:横坐标,右移加,左移减;纵坐标,上移加,下移减即可解决问题;
【详解】由题意P(﹣5,4),向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是(﹣1,2),
故选:A.
【点睛】本题考查坐标与平移,解题的关键是记住平移规律:坐标,右移加,左移减;纵坐标,上移加,属于中考常考题型.
3.(-4,3)或(0,3)
【分析】根据点M坐标为(-2,3),轴,且线段MN=2,可以得到点N的纵坐标为3,横坐标为-2-2=-4或-2+2=0,然后即可写出点N的坐标.
【详解】解:∵点M坐标为(-2,3),轴,
∴点N的纵坐标为3,
又∵线段MN=2,
∴点N的横坐标为-2-2=-4或-2+2=0,
∴点N的坐标为(-4,3)或(0,3),
故答案为:(-4,3)或(0,3).
【点睛】本题考查坐标与图形的性质、平面直角坐标系,解答本题的关键是明确平行于x轴的直线的特点:纵坐标都相等,横坐标差的绝对值就是这两点之间的距离.
4.
【分析】根据题意可得点C的纵坐标,横坐标的可能值,进而根据点C在第三象限得到点C的具体坐标.
【详解】解:点C距离x轴2个单位长度,
点C的纵坐标可能的值为,
点C距离y轴3个单位长度,
点C的横坐标可能的值为,
点C在第三象限,
点C的坐标为,
故答案为.
【点睛】本题主要考查点的坐标的相关知识;用到的知识点为:点到x轴的距离为点的纵坐标的绝对值;点到y轴的距离为点的横坐标的绝对值.
5.四
【分析】根据各象限内点的坐标特征解答.
【详解】点P(2,-3)在第四象限.
故答案为四.
【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
6.3
【分析】在y轴上的点横坐标为零,即a-3=0,即可解答
【详解】解:∵点M(a-3,a+4)在y轴上
∴a-3=0
∴a=3
故答案为∶3
【点睛】本题考查了平面直角坐标系中点的坐标特征.第一象限内点的坐标特征为(+,+),第二象限内点的坐标特征为(-,+),第三象限内点的坐标特征为(-,-),第四象限内点的坐标特征为(+,-),x轴上的点纵坐标为0,y轴上的点横坐标为0.
7.(0,-1)
【分析】根据y轴上点的横坐标为0列方程求出a的值,再求解即可.
【详解】∵点在y轴上,
∴,
解得a=2,
∴,
∴点P的坐标为(0,-1).
故答案为:(0,-1).
【点睛】本题主要考查了点的坐标,根据在y轴上点的坐标是解题的关键.
8.12
【分析】根据A和两点的纵坐标相等,可得线段的长,再根据点的纵坐标,可得以为底的的高,从而的面积可求.
【详解】解:点,
,
,
点在直线上,
∵直线AB:与直线平行,且平行线间的距离为,
故答案为:.
【点睛】本题考查了三角形的面积计算,明确平面直角坐标系中的点的坐标特点及求相应线段的长,是解题的关键.
9.
【分析】根据题意和图象中的点的坐标,可以发现这些点的变化规律,从而可以求得第56个点的坐标.
【详解】解:由题意可得,横坐标是的点有个,横坐标是的点有个,横坐标是的点有个,…,
,
第个点的坐标为,
故答案为
【点睛】本题考查规律性:点的坐标,解答本题的关键是明确题意,发现题目中点的变化规律,求出相应的点的坐标.
10.(3,0)
【分析】根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2023除以6,根据商和余数的情况确定所对应的点的坐标即可.
【详解】解:如图,根据反射角与入射角的定义作出图形,
根据图形可以得到:每6次反弹为一个循环组依次循环,经过6次反弹后动点回到出发点(0,3),
∵2023÷6=337…1,
当点P第2023次碰到矩形的边时为第338个循环组的第1次反弹,点P的坐标为(3,0),
故答案为:(3,0).
【点睛】本题考查了矩形的性质、点的坐标的规律;作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
11.
【分析】根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2021除以4,根据商和余数的情况确定点A2021的坐标即可.
【详解】解:∵A1的坐标为(3,1),
∴A2(0,4),A3( 3,1),A4(0, 2),A5(3,1),
…,
依此类推,每4个点为一个循环组依次循环,
∵2021÷4=505…1,
∴的坐标与A1的坐标相同,为(3,1).
故答案是:(3,1).
【点睛】考查点的坐标规律,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键.
12.
【分析】根据平移规律:横坐标右移加,左移减;纵坐标上移加,下移减即可得.
【详解】解:平移后点Q的坐标为(-1-1,2-2),即(-2,0),
故答案为:(-2,0).
【点睛】此题主要考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.掌握点的坐标的变化规律是解题的关键.
13.(7,0)
【分析】根据B点横坐标与A点横坐标之差和E点横坐标与D点横坐标之差相等即可求解.
【详解】解:由题意知:A、B两点之间的横坐标差为:,
由平移性质可知:E、D两点横坐标之差与B、A两点横坐标之差相等,
设E点横坐标为a,
则a-6=1,∴a=7,
∴E点坐标为(7,0) .
故答案为:(7,0) .
【点睛】本题考查了图形的平移规律,平移前后对应点的线段长度不发生变化,熟练掌握平移的性质是解决此题的关键.
14.-3
【分析】点坐标向上平移2个单位,就是纵坐标加上2,落在x轴上,就是纵坐标为0,求出m的值.
【详解】解:点向上平移2个单位得,
∵平移后落在x轴上,
∴,解得.
故答案是:-3.
【点睛】本题考查点坐标的平移,解题的关键是掌握点坐标平移的方法.
15.(1011,1011)
【分析】观察图象可知,偶数点在第一象限,由题意,,,,,即可解决问题.
【详解】解:观察图象可知,偶数点在第一象限,
,,,,,
,
故答案为:.
【点睛】本题考查坐标与图形变化平移,规律型等知识,解题的关键是学会探究规律,利用规律解决问题,属于中考常考题型.
16.-10
【分析】根据平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,分别列式求出x、y的值,然后相乘计算即可得解.
【详解】∵点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),
∴x=-3-2=-5,y-3=-1,
解得y=2,
∴xy=-5×2=-10.
故答案为-10.
【点睛】本题考查了坐标与图形变化-平移,熟记平移中点的变化规律是解题的关键.
17.(1)画图见解析,
(2)3.5
【分析】(1)根据题意可得,顺次连接平移后的各点可得到三角形A′B′C′;
(2)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案.
【详解】(1)解:根据题意得:,顺次连接平移后的各点可得到三角形A′B′C′,
如图所示,三角形A′B′C′即为所求:
;
(2)△ABC的面积= .
【点睛】本题主要考查了三角形面积求法以及坐标系内图形平移,正确得出对应点位置是解题关键.
18.(1)见解析
(2)体育馆和食堂的位置见解析;教学楼到体育馆的距离为750米
【分析】(1)根据点A的坐标即可确定原点的位置;
(2)由(1)可直接标出C,D的位置,进而即可求解.
【详解】(1)解:根据点A、B的坐标,确定原点O,建立平面直角坐标系,如图所示:
(2)体育馆和食堂的位置如上图所示,教学楼到体育馆的距离为5×150=750(米).
【点睛】本题主要考查平面直角坐标系的应用,关键是要能根据已知点的坐标确定原点的位置,然后才能标出其他点的坐标.
19.(1)P1(x-4,y+4)
(2)图见解析,B1(-3,-1),C1(1,1)
【分析】(1)根据点A(4,0)经过平移后对应点为A1(0,4),可得平移规律是左移4个单位,上移4个单位;进而可以解决问题;
(2)结合(1)平移规律即可画出平移后的△A1B1C1,进而写出B1、C1的坐标.
(1)解:∵点A(4,0)经过平移后对应点为A1(0,4),∴P1(x﹣4,y+4);故答案为:(x﹣4,y+4);
(2)如图所示,△A1B1C1即为所求;由图可知:B1(﹣3,﹣1),C1(1,1).
【点睛】本题考查了作图﹣平移变换,解决本题的关键是掌握平移性质.
20.(1)见解析;(2);(3).
【分析】(1)根据A、C两点坐标根据平面直角坐标系即可;
(2)首先确定A、B、C三点向左平移5个单位长度,再向下平移6个单位长度的对应点位置,然后再连接即可;;
(3)利用此平移规律可得.
【详解】解:(1)如图所示;
(2)如图所示:点B坐标为:(1,3);将先向左平移5个单位长度,再向下平移6个单位长度,画出两次平移后的,即为所求,点的对应点的坐标;
(3)先向左平移5个单位长度,再向下平移6个单位长度,可得.
【点睛】本题考查了平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
一、单选题
1.(2022春·甘肃武威·七年级统考期末)若点在第二象限,则点在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2022春·甘肃陇南·七年级统考期末)如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )
A.(﹣1,2) B.(﹣9,6) C.(﹣1,6) D.(﹣9,2)
二、填空题
3.(2022春·甘肃武威·七年级统考期末)在平面直角坐标系中,点坐标为,若轴,且线段,则点坐标为__________.
4.(2022春·甘肃陇南·七年级统考期末)点在第三象限,距离轴个单位长度,距离轴个单位长度,则点的坐标为______.
5.(2022春·甘肃武威·七年级统考期末)在平面直角坐标系中,点P(2,﹣3)在__________象限.
6.(2022春·甘肃嘉峪关·七年级统考期末)若点M(a-3,a+4)在y轴上,则a=___________.
7.(2022春·甘肃陇南·七年级统考期末)已知点在轴上,则点的坐标为__________.
8.(2022春·甘肃武威·七年级统考期末)平面直角坐标系中,由点组成的的面积是______.
9.(2022春·甘肃陇南·七年级统考期末)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如,,,,,,根据这个规律探索可得,第个点的坐标为_____.
10.(2022春·甘肃武威·七年级统考期末)如图,弹性小球从点出发,沿所示方向运动,每当小球碰到长方形的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为,第2次碰到矩形的边时的点为,…,第次碰到矩形的边时的点为,则点的坐标是__________.
11.(2022春·甘肃武威·七年级统考期末)在平面直角坐标系中,对于点我们把叫做点P的伴随点,已知的伴随点为,点的伴随点为,点的伴随点为,这样依次得到,若点的坐标为,则点的坐标为_______
12.(2022春·甘肃陇南·七年级统考期末)在平面直角坐标系中,将点向下平移2个单位长度,再向左平移1个单位长度得到点,则点的坐标为________.
13.(2022春·甘肃陇南·七年级统考期末)如图,在平面直角坐标系中,的顶点,的坐标分别为,,把沿轴向右平移得到,如果点的坐标为,则点的坐标为__________.
14.(2022春·甘肃陇南·七年级统考期末)将点向上平移2个单位后落在轴上,则___.
15.(2022春·甘肃定西·七年级统考期末)如图,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点,…,按此作法进行下去,则点的坐标为_____.
16.(2022春·甘肃武威·七年级统考期末)将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则__________.
三、解答题
17.(2022春·甘肃定西·七年级统考期末)如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系.已知三角形ABC的顶点A的坐标为,顶点B的坐标为,顶点C的坐标为.
(1)把三角形ABC向右平移5个单位长度,再向下平移4个单位长度得到三角形,请你画出三角形,并直接写出点,,的坐标.
(2)三角形ABC的面积为______个平方单位.
18.(2022春·甘肃平凉·七年级统考期末)如图为某中学新校区分布图的一部分,方格纸中每个小方格都是边长为1个单位长度的正方形,若教学楼的坐标为,图书馆的坐标为,解答下列问题:
(1)在图中找到坐标系中的原点,并建立平面直角坐标系;
(2)若体育馆的坐标为,食堂的坐标为,请在图中标出体育馆和食堂的位置,并求出教学楼到体育馆的距离(1格=150米).
19.(2022春·甘肃武威·七年级统考期末)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(4,0),,C(5,-3),点A经过平移后对应点为A1(0,4),将△ABC作同样的平移得到△A1B1C1.
(1)若边上一点经过上述平移后的对应点为,用含,的式子表示点的坐标为________(直接写出结果即可).
(2)在图中画出平移后的△A1B1C1并写出B1、C1的坐标.
20.(2022春·甘肃陇南·七年级统考期末)如图,在边长为1个单位长度的小正方形组成的网格中,格点三角形(顶点为网格线的交点)的顶点,的坐标分别为,.
(1)请在网格图中建立平面直角坐标系;
(2)将先向左平移5个单位长度,再向下平移6个单位长度,请画出两次平移后的,并直接写出点的对应点的坐标;
(3)若是内一点,直接写出中的对应点的坐标.
参考答案:
1.C
【分析】根据第二象限内的点的横坐标小于零,纵坐标大于零,可得关于a、b的不等式,再根据不等式的性质,可得B点的坐标符号.
【详解】解:根据题意知,
解得:a<﹣1,b>2,
则a-3<0,1-b<0,
∴点在第三象限,
故选:C.
【点睛】本题考查了点的坐标,利用第二象限内点的横坐标小于零,纵坐标大于零得出不等式,又利用不等式的性质得出B点的坐标符号是解题关键.
2.A
【分析】根据平移规律:横坐标,右移加,左移减;纵坐标,上移加,下移减即可解决问题;
【详解】由题意P(﹣5,4),向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是(﹣1,2),
故选:A.
【点睛】本题考查坐标与平移,解题的关键是记住平移规律:坐标,右移加,左移减;纵坐标,上移加,属于中考常考题型.
3.(-4,3)或(0,3)
【分析】根据点M坐标为(-2,3),轴,且线段MN=2,可以得到点N的纵坐标为3,横坐标为-2-2=-4或-2+2=0,然后即可写出点N的坐标.
【详解】解:∵点M坐标为(-2,3),轴,
∴点N的纵坐标为3,
又∵线段MN=2,
∴点N的横坐标为-2-2=-4或-2+2=0,
∴点N的坐标为(-4,3)或(0,3),
故答案为:(-4,3)或(0,3).
【点睛】本题考查坐标与图形的性质、平面直角坐标系,解答本题的关键是明确平行于x轴的直线的特点:纵坐标都相等,横坐标差的绝对值就是这两点之间的距离.
4.
【分析】根据题意可得点C的纵坐标,横坐标的可能值,进而根据点C在第三象限得到点C的具体坐标.
【详解】解:点C距离x轴2个单位长度,
点C的纵坐标可能的值为,
点C距离y轴3个单位长度,
点C的横坐标可能的值为,
点C在第三象限,
点C的坐标为,
故答案为.
【点睛】本题主要考查点的坐标的相关知识;用到的知识点为:点到x轴的距离为点的纵坐标的绝对值;点到y轴的距离为点的横坐标的绝对值.
5.四
【分析】根据各象限内点的坐标特征解答.
【详解】点P(2,-3)在第四象限.
故答案为四.
【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
6.3
【分析】在y轴上的点横坐标为零,即a-3=0,即可解答
【详解】解:∵点M(a-3,a+4)在y轴上
∴a-3=0
∴a=3
故答案为∶3
【点睛】本题考查了平面直角坐标系中点的坐标特征.第一象限内点的坐标特征为(+,+),第二象限内点的坐标特征为(-,+),第三象限内点的坐标特征为(-,-),第四象限内点的坐标特征为(+,-),x轴上的点纵坐标为0,y轴上的点横坐标为0.
7.(0,-1)
【分析】根据y轴上点的横坐标为0列方程求出a的值,再求解即可.
【详解】∵点在y轴上,
∴,
解得a=2,
∴,
∴点P的坐标为(0,-1).
故答案为:(0,-1).
【点睛】本题主要考查了点的坐标,根据在y轴上点的坐标是解题的关键.
8.12
【分析】根据A和两点的纵坐标相等,可得线段的长,再根据点的纵坐标,可得以为底的的高,从而的面积可求.
【详解】解:点,
,
,
点在直线上,
∵直线AB:与直线平行,且平行线间的距离为,
故答案为:.
【点睛】本题考查了三角形的面积计算,明确平面直角坐标系中的点的坐标特点及求相应线段的长,是解题的关键.
9.
【分析】根据题意和图象中的点的坐标,可以发现这些点的变化规律,从而可以求得第56个点的坐标.
【详解】解:由题意可得,横坐标是的点有个,横坐标是的点有个,横坐标是的点有个,…,
,
第个点的坐标为,
故答案为
【点睛】本题考查规律性:点的坐标,解答本题的关键是明确题意,发现题目中点的变化规律,求出相应的点的坐标.
10.(3,0)
【分析】根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2023除以6,根据商和余数的情况确定所对应的点的坐标即可.
【详解】解:如图,根据反射角与入射角的定义作出图形,
根据图形可以得到:每6次反弹为一个循环组依次循环,经过6次反弹后动点回到出发点(0,3),
∵2023÷6=337…1,
当点P第2023次碰到矩形的边时为第338个循环组的第1次反弹,点P的坐标为(3,0),
故答案为:(3,0).
【点睛】本题考查了矩形的性质、点的坐标的规律;作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
11.
【分析】根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2021除以4,根据商和余数的情况确定点A2021的坐标即可.
【详解】解:∵A1的坐标为(3,1),
∴A2(0,4),A3( 3,1),A4(0, 2),A5(3,1),
…,
依此类推,每4个点为一个循环组依次循环,
∵2021÷4=505…1,
∴的坐标与A1的坐标相同,为(3,1).
故答案是:(3,1).
【点睛】考查点的坐标规律,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键.
12.
【分析】根据平移规律:横坐标右移加,左移减;纵坐标上移加,下移减即可得.
【详解】解:平移后点Q的坐标为(-1-1,2-2),即(-2,0),
故答案为:(-2,0).
【点睛】此题主要考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.掌握点的坐标的变化规律是解题的关键.
13.(7,0)
【分析】根据B点横坐标与A点横坐标之差和E点横坐标与D点横坐标之差相等即可求解.
【详解】解:由题意知:A、B两点之间的横坐标差为:,
由平移性质可知:E、D两点横坐标之差与B、A两点横坐标之差相等,
设E点横坐标为a,
则a-6=1,∴a=7,
∴E点坐标为(7,0) .
故答案为:(7,0) .
【点睛】本题考查了图形的平移规律,平移前后对应点的线段长度不发生变化,熟练掌握平移的性质是解决此题的关键.
14.-3
【分析】点坐标向上平移2个单位,就是纵坐标加上2,落在x轴上,就是纵坐标为0,求出m的值.
【详解】解:点向上平移2个单位得,
∵平移后落在x轴上,
∴,解得.
故答案是:-3.
【点睛】本题考查点坐标的平移,解题的关键是掌握点坐标平移的方法.
15.(1011,1011)
【分析】观察图象可知,偶数点在第一象限,由题意,,,,,即可解决问题.
【详解】解:观察图象可知,偶数点在第一象限,
,,,,,
,
故答案为:.
【点睛】本题考查坐标与图形变化平移,规律型等知识,解题的关键是学会探究规律,利用规律解决问题,属于中考常考题型.
16.-10
【分析】根据平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,分别列式求出x、y的值,然后相乘计算即可得解.
【详解】∵点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),
∴x=-3-2=-5,y-3=-1,
解得y=2,
∴xy=-5×2=-10.
故答案为-10.
【点睛】本题考查了坐标与图形变化-平移,熟记平移中点的变化规律是解题的关键.
17.(1)画图见解析,
(2)3.5
【分析】(1)根据题意可得,顺次连接平移后的各点可得到三角形A′B′C′;
(2)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案.
【详解】(1)解:根据题意得:,顺次连接平移后的各点可得到三角形A′B′C′,
如图所示,三角形A′B′C′即为所求:
;
(2)△ABC的面积= .
【点睛】本题主要考查了三角形面积求法以及坐标系内图形平移,正确得出对应点位置是解题关键.
18.(1)见解析
(2)体育馆和食堂的位置见解析;教学楼到体育馆的距离为750米
【分析】(1)根据点A的坐标即可确定原点的位置;
(2)由(1)可直接标出C,D的位置,进而即可求解.
【详解】(1)解:根据点A、B的坐标,确定原点O,建立平面直角坐标系,如图所示:
(2)体育馆和食堂的位置如上图所示,教学楼到体育馆的距离为5×150=750(米).
【点睛】本题主要考查平面直角坐标系的应用,关键是要能根据已知点的坐标确定原点的位置,然后才能标出其他点的坐标.
19.(1)P1(x-4,y+4)
(2)图见解析,B1(-3,-1),C1(1,1)
【分析】(1)根据点A(4,0)经过平移后对应点为A1(0,4),可得平移规律是左移4个单位,上移4个单位;进而可以解决问题;
(2)结合(1)平移规律即可画出平移后的△A1B1C1,进而写出B1、C1的坐标.
(1)解:∵点A(4,0)经过平移后对应点为A1(0,4),∴P1(x﹣4,y+4);故答案为:(x﹣4,y+4);
(2)如图所示,△A1B1C1即为所求;由图可知:B1(﹣3,﹣1),C1(1,1).
【点睛】本题考查了作图﹣平移变换,解决本题的关键是掌握平移性质.
20.(1)见解析;(2);(3).
【分析】(1)根据A、C两点坐标根据平面直角坐标系即可;
(2)首先确定A、B、C三点向左平移5个单位长度,再向下平移6个单位长度的对应点位置,然后再连接即可;;
(3)利用此平移规律可得.
【详解】解:(1)如图所示;
(2)如图所示:点B坐标为:(1,3);将先向左平移5个单位长度,再向下平移6个单位长度,画出两次平移后的,即为所求,点的对应点的坐标;
(3)先向左平移5个单位长度,再向下平移6个单位长度,可得.
【点睛】本题考查了平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
