图形的平移与旋转[上学期]
图片预览







文档简介
课件32张PPT。平移与旋转复习复习回顾(小组合作互相提问)1.什么是图形的平移?平移的特征是什么?2.什么是图形的旋转?旋转的特征是什么?3.什么是旋转对称图形?它和中心对称图形有什么区别?4.什么是中心对称图形?什么叫两个图形成中心对称?5.如果两个图形成中心对称图形,那么它们有什么特征?6.两个图形成中心对称的识别方法是什么?7.图形的三种主要变换:平移、旋转、轴对称有什么共同的特征?(一)图形的平移 1、概念:图形的平行移动,简称为平移。 平移由移动的方向和距离所决定。2、平移的特征:
(1)对应线段平行(或在一条直线上)且相等;对应角相等;
(2)对应点所连的线段平行(或在一条直线上)且相等;
(3)图形在平移后形状和大小没有发生变化.请你选一选
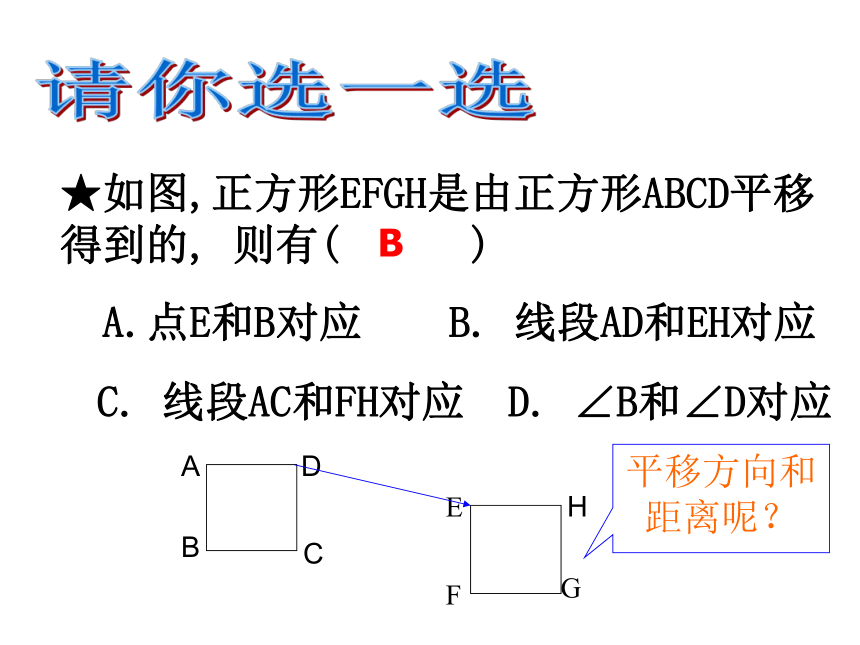
★如图,正方形EFGH是由正方形ABCD平移得到的, 则有( )
A.点E和B对应 B. 线段AD和EH对应
C. 线段AC和FH对应 D. ∠B和∠D对应
B平移方向和距离呢?旋转方向2、旋转的特征:
(1)图形中每一点都绕着旋转中心旋转了同样大小的角度;
(2)对应点到旋转中心的距离相等;
(3)对应线段相等,对应角相等;
(4)图形的形状和大小都没有发生变化.
(二)图形的旋转
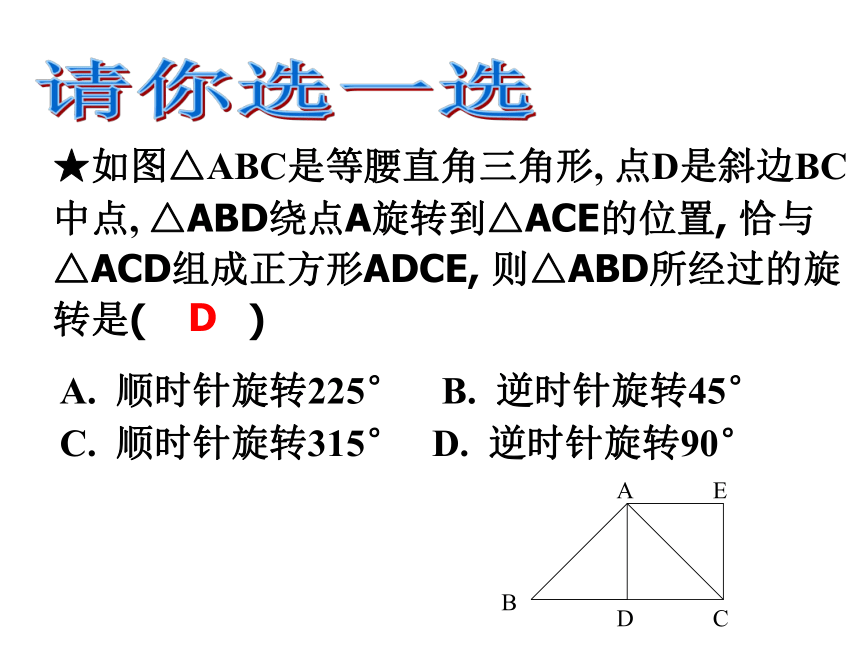
1、概念:图形的旋转是将一个图形绕着一点按顺(逆)时针转过某个角度;★如图△ABC是等腰直角三角形, 点D是斜边BC中点, △ABD绕点A旋转到△ACE的位置, 恰与△ACD组成正方形ADCE, 则△ABD所经过的旋转是( )
A. 顺时针旋转225° B. 逆时针旋转45°
C. 顺时针旋转315° D. 逆时针旋转90°D请你选一选★以下四家银行行标中,不是旋转对称图形的有 ( )
A. B. C. D.
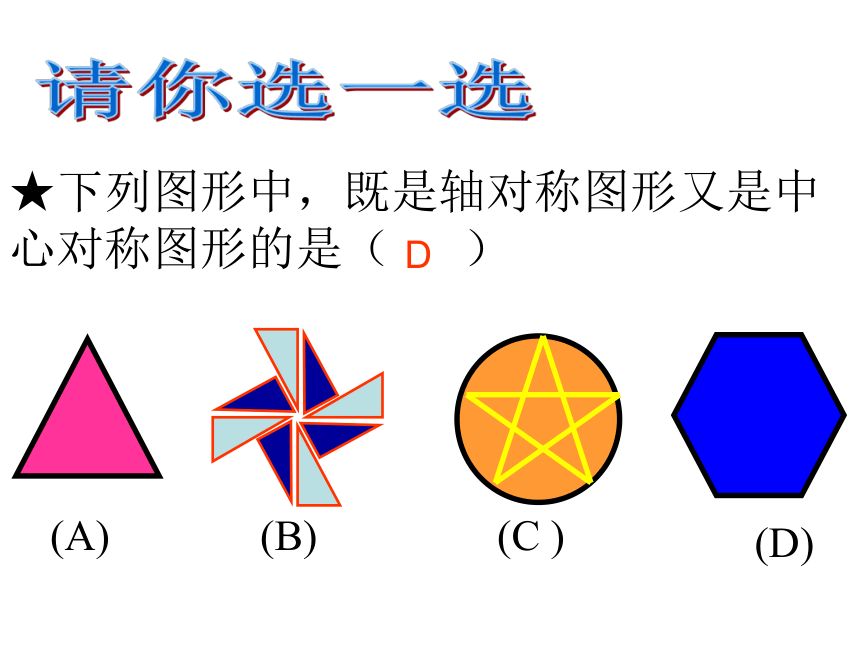
B(三)旋转对称图形概念:绕着某一点转动一定角度后,能与自身重合的图形称为旋转对称图形. 1 、定义:把一个图形绕着某一个点旋转180°,能与自身重合,那么就说这个图形叫做中心对称图形。 2、定义:把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就说这两个图形成中心对称。(四)中心对称图形3、成中心对称的两个图形的特征 在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。 如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这一点成中心对称。4、成中心对称的识别方法★下列图形中,既是轴对称图形又是中心对称图形的是( )请你选一选D共同特征:变换后图形的形状和大小都没有改变,线段的长度和角的大小都不变,前后两个图形能完全重合,即是全等图形.(五)图形的三种主要变换:
平移、旋转、轴对称(四)画法1、经过平移,△ABC的边AB移到了EF,作出平移后的三角形.EF2、在右图中作出“三角旗”绕O点按逆时针旋转90°后的图案.3、已知四边形ABCD和点O,画四边形A'B'C'D' 使它与已知四边形关于点O对称。画法:四边形A'B'C'D'就是所求的四边形。1. 下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到B2、如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=700,则( ).
A. FG=5, ∠G=700 B. EH=5, ∠F=700
C. EF=5, ∠F=700 D. EF=5. ∠E=700 ABCDEFHGB3.将图形 按顺时针方向旋转90度后的图形是( ) A B C DC4.下列图形中,不能由图形 M 经过一次平移或旋转得到的是( ).ABCDMC5、如图,ΔABC和ΔADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到左图,再将左图作为“基本图形”绕着A点经过逆时针连续旋转得到右图.两次旋转的角度分别为( ). A、45°,90° B、90°,45°
C、60°,30° D、30°,60°A6、如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( ).
A. ΔABC和ΔADE B. ΔABC和ΔABD
C. ΔABD和ΔACE D. ΔACE和ΔADEC7、在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
A、100 B、150 C、200 D、250
B(1)通过平移变换但不能通过旋转变换得到的图是_________; ①②③④⑤⑥① ⑤② ⑥③ ④(2)可以通过旋转变换但不能通过平移
变换得到的图案是____
(3)既可以由平移变换, 也可以由旋转变换得到 的图案是_____
8下列图形均可以由“基本图案”通过变换得到(序号)
9、如图:ΔDEF可以看作ΔABC平移得到
1)AB∥ ; ∥ .
2)若BC=5cm, CE =3cm,则平移的
距离是 ,EF= cm.
3)若连结AD,与AD相等的线段是: .DEACDF2cm5BE或CFDE
9、如图,在ΔABC中,∠A=40o,∠C=35o,将ΔABC平移得到ΔDEF的位置,DF与BC交于点G, 你能求出∠DGB与∠E的度数吗?
10、如图:在梯形ABCD中,AD∥BC,∠B+∠C=90o,点E在AD上,先将AB向右平移,使点A与点E重合,交BC于F,再将DC向左平移,使点D与点E重合,交BC于G,请判断ΔEFG的形状
“若AD=3,FG=5,
求BC的长”11、请说出下面乙树是怎样由甲树变换得到的?如图,点E为正方形ABCD的边CD上一点,AB=5,DE=6。△DAE旋转后能与△DCF重合,(1)旋转中心是哪一点?(2)旋转了多少度?(3)如果连接EF,那么△DEF是怎样的三角形?(4)四边形DEBF的周长和面积?
?
?
?13、已知正方形ABCD和正方形AEFG有一个公共点A,若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并说明理由.◆、 如图,在纸上画△ABC和两条直线m、n.分三种情况分别画出△ABC关于直线m对称的△A′B′C′,再画出△A′B′C′关于直线n对称的△A′′B′′C′′.并观察△ABC和△A′′B′′C′′,你能发现这两个三角形有什么关系吗?情况(1):直线m、n互相平行; 情况(2):直线m、n互相垂直; 情况(3):直线m、n相交但不垂直.
情况(1):直线m、n互相平行; 情况(1)如图所示,△ABC和△A′′B′′C′′是平移的关系,平移的方向就是点A到点A′′的方向,平移的距离是线段A A′′的长度.画一画情况(2):直线m、n互相垂直; 情况(2)如图所示,△ABC和△A′′B′′C′′成中心对称的关系,对称中心是直线m、n的交点.画一画画一画情况(3):直线m、n相交但不垂直.情况(3)如图所示,△ABC和△A′′B′′C′′成旋转对称的关系,旋转中心是直线m、n的交点O,旋转角度是∠AO A′′的度数.
(1)对应线段平行(或在一条直线上)且相等;对应角相等;
(2)对应点所连的线段平行(或在一条直线上)且相等;
(3)图形在平移后形状和大小没有发生变化.请你选一选
★如图,正方形EFGH是由正方形ABCD平移得到的, 则有( )
A.点E和B对应 B. 线段AD和EH对应
C. 线段AC和FH对应 D. ∠B和∠D对应
B平移方向和距离呢?旋转方向2、旋转的特征:
(1)图形中每一点都绕着旋转中心旋转了同样大小的角度;
(2)对应点到旋转中心的距离相等;
(3)对应线段相等,对应角相等;
(4)图形的形状和大小都没有发生变化.
(二)图形的旋转
1、概念:图形的旋转是将一个图形绕着一点按顺(逆)时针转过某个角度;★如图△ABC是等腰直角三角形, 点D是斜边BC中点, △ABD绕点A旋转到△ACE的位置, 恰与△ACD组成正方形ADCE, 则△ABD所经过的旋转是( )
A. 顺时针旋转225° B. 逆时针旋转45°
C. 顺时针旋转315° D. 逆时针旋转90°D请你选一选★以下四家银行行标中,不是旋转对称图形的有 ( )
A. B. C. D.
B(三)旋转对称图形概念:绕着某一点转动一定角度后,能与自身重合的图形称为旋转对称图形. 1 、定义:把一个图形绕着某一个点旋转180°,能与自身重合,那么就说这个图形叫做中心对称图形。 2、定义:把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就说这两个图形成中心对称。(四)中心对称图形3、成中心对称的两个图形的特征 在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。 如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这一点成中心对称。4、成中心对称的识别方法★下列图形中,既是轴对称图形又是中心对称图形的是( )请你选一选D共同特征:变换后图形的形状和大小都没有改变,线段的长度和角的大小都不变,前后两个图形能完全重合,即是全等图形.(五)图形的三种主要变换:
平移、旋转、轴对称(四)画法1、经过平移,△ABC的边AB移到了EF,作出平移后的三角形.EF2、在右图中作出“三角旗”绕O点按逆时针旋转90°后的图案.3、已知四边形ABCD和点O,画四边形A'B'C'D' 使它与已知四边形关于点O对称。画法:四边形A'B'C'D'就是所求的四边形。1. 下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到B2、如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=700,则( ).
A. FG=5, ∠G=700 B. EH=5, ∠F=700
C. EF=5, ∠F=700 D. EF=5. ∠E=700 ABCDEFHGB3.将图形 按顺时针方向旋转90度后的图形是( ) A B C DC4.下列图形中,不能由图形 M 经过一次平移或旋转得到的是( ).ABCDMC5、如图,ΔABC和ΔADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到左图,再将左图作为“基本图形”绕着A点经过逆时针连续旋转得到右图.两次旋转的角度分别为( ). A、45°,90° B、90°,45°
C、60°,30° D、30°,60°A6、如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( ).
A. ΔABC和ΔADE B. ΔABC和ΔABD
C. ΔABD和ΔACE D. ΔACE和ΔADEC7、在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
A、100 B、150 C、200 D、250
B(1)通过平移变换但不能通过旋转变换得到的图是_________; ①②③④⑤⑥① ⑤② ⑥③ ④(2)可以通过旋转变换但不能通过平移
变换得到的图案是____
(3)既可以由平移变换, 也可以由旋转变换得到 的图案是_____
8下列图形均可以由“基本图案”通过变换得到(序号)
9、如图:ΔDEF可以看作ΔABC平移得到
1)AB∥ ; ∥ .
2)若BC=5cm, CE =3cm,则平移的
距离是 ,EF= cm.
3)若连结AD,与AD相等的线段是: .DEACDF2cm5BE或CFDE
9、如图,在ΔABC中,∠A=40o,∠C=35o,将ΔABC平移得到ΔDEF的位置,DF与BC交于点G, 你能求出∠DGB与∠E的度数吗?
10、如图:在梯形ABCD中,AD∥BC,∠B+∠C=90o,点E在AD上,先将AB向右平移,使点A与点E重合,交BC于F,再将DC向左平移,使点D与点E重合,交BC于G,请判断ΔEFG的形状
“若AD=3,FG=5,
求BC的长”11、请说出下面乙树是怎样由甲树变换得到的?如图,点E为正方形ABCD的边CD上一点,AB=5,DE=6。△DAE旋转后能与△DCF重合,(1)旋转中心是哪一点?(2)旋转了多少度?(3)如果连接EF,那么△DEF是怎样的三角形?(4)四边形DEBF的周长和面积?
?
?
?13、已知正方形ABCD和正方形AEFG有一个公共点A,若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并说明理由.◆、 如图,在纸上画△ABC和两条直线m、n.分三种情况分别画出△ABC关于直线m对称的△A′B′C′,再画出△A′B′C′关于直线n对称的△A′′B′′C′′.并观察△ABC和△A′′B′′C′′,你能发现这两个三角形有什么关系吗?情况(1):直线m、n互相平行; 情况(2):直线m、n互相垂直; 情况(3):直线m、n相交但不垂直.
情况(1):直线m、n互相平行; 情况(1)如图所示,△ABC和△A′′B′′C′′是平移的关系,平移的方向就是点A到点A′′的方向,平移的距离是线段A A′′的长度.画一画情况(2):直线m、n互相垂直; 情况(2)如图所示,△ABC和△A′′B′′C′′成中心对称的关系,对称中心是直线m、n的交点.画一画画一画情况(3):直线m、n相交但不垂直.情况(3)如图所示,△ABC和△A′′B′′C′′成旋转对称的关系,旋转中心是直线m、n的交点O,旋转角度是∠AO A′′的度数.
