第七章 图形的平移与旋转[下学期]
文档属性
| 名称 | 第七章 图形的平移与旋转[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 108.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-21 16:41:00 | ||
图片预览

文档简介
第七章 图形的平移与旋转
一、基础知识梳理
1.平移的定义与规律
(1)定义:在平面内将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
关键:平移不改变图形的形状和大小,也不会改变图形的方向.
(2)平移的规律:经过平移,对应线段、对应角分别相等,对应点所连的线段平行且相等(或共线且相等).
(3)简单作图
平移的作图主要关注要点:1.方向,2.距离.整个平移的作图,就象把整个图案的每个特征点放在一套平行的轨道上滑动一样,每个特征点滑过的距离是一样的.
2.旋转的定义与规律
(1)定义:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.
关键:旋转不改变图形的大小和形状,但改变图形的方向.
(2)旋转的规律
经过旋转,图形上的每一点,都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.
(3)简单的旋转作图
旋转作图关键有两点:①旋转方向,②旋转角度.主要分四步:边、转、截、连.旋转就象把每个特征点与旋转中心用线连住的风筝,每个点转的角度是相同的,每个点与旋转中心的距离是不会改变的,即对应点与旋转中心距离相等.
3.图案的分析与设计
首先找到图中的基本图案,然后分析其图案与它的关系,即由它作何种运动变换而形成的,我们主要遇到的变换有:轴对称、平移、旋转.在相似形一章里还会学到图形的放大与缩小等.
二、考点与命题趋向分析
(一)能力
1.图形的平移
(1)通过具体实例认识平移,探索它的基本性质,理解对应点连线平行且相等的性质.
(2)能按要求作出简单平面图形平移后的图形.
(3)利用平移进行图案设计,认识和欣赏平移在现实生活中的应用.
2.图形的旋转.
(1)通过具体实例认识旋转,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质.
(2)了解平行四边形、圆是中心对称图形.
(3)能够按要求作出简单平面图形旋转后的图形.
(4)欣赏旋转在现实生活中的应用.
(5)探索图形之间的变换关系(轴对称、平移、旋转及其组合).
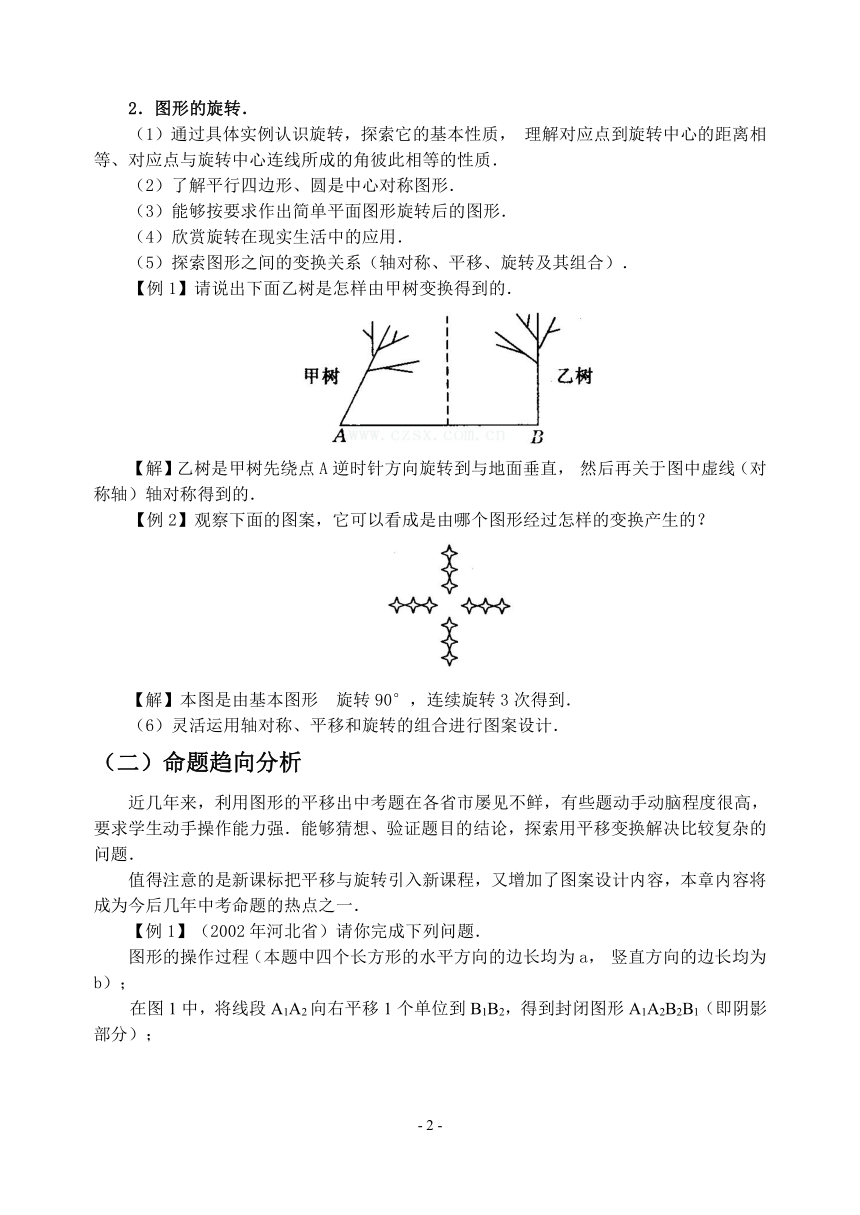
【例1】请说出下面乙树是怎样由甲树变换得到的.
【解】乙树是甲树先绕点A逆时针方向旋转到与地面垂直,然后再关于图中虚线(对称轴)轴对称得到的.
【例2】观察下面的图案,它可以看成是由哪个图形经过怎样的变换产生的?
【解】本图是由基本图形 旋转90°,连续旋转3次得到.
(6)灵活运用轴对称、平移和旋转的组合进行图案设计.
(二)命题趋向分析
近几年来,利用图形的平移出中考题在各省市屡见不鲜,有些题动手动脑程度很高,要求学生动手操作能力强.能够猜想、验证题目的结论,探索用平移变换解决比较复杂的问题.
值得注意的是新课标把平移与旋转引入新课程,又增加了图案设计内容,本章内容将成为今后几年中考命题的热点之一.
【例1】(2002年河北省)请你完成下列问题.
图形的操作过程(本题中四个长方形的水平方向的边长均为a,竖直方向的边长均为b);
在图1中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分);
(1) (2) (3)
在图2中,将折线A1A2A3向右平移1个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
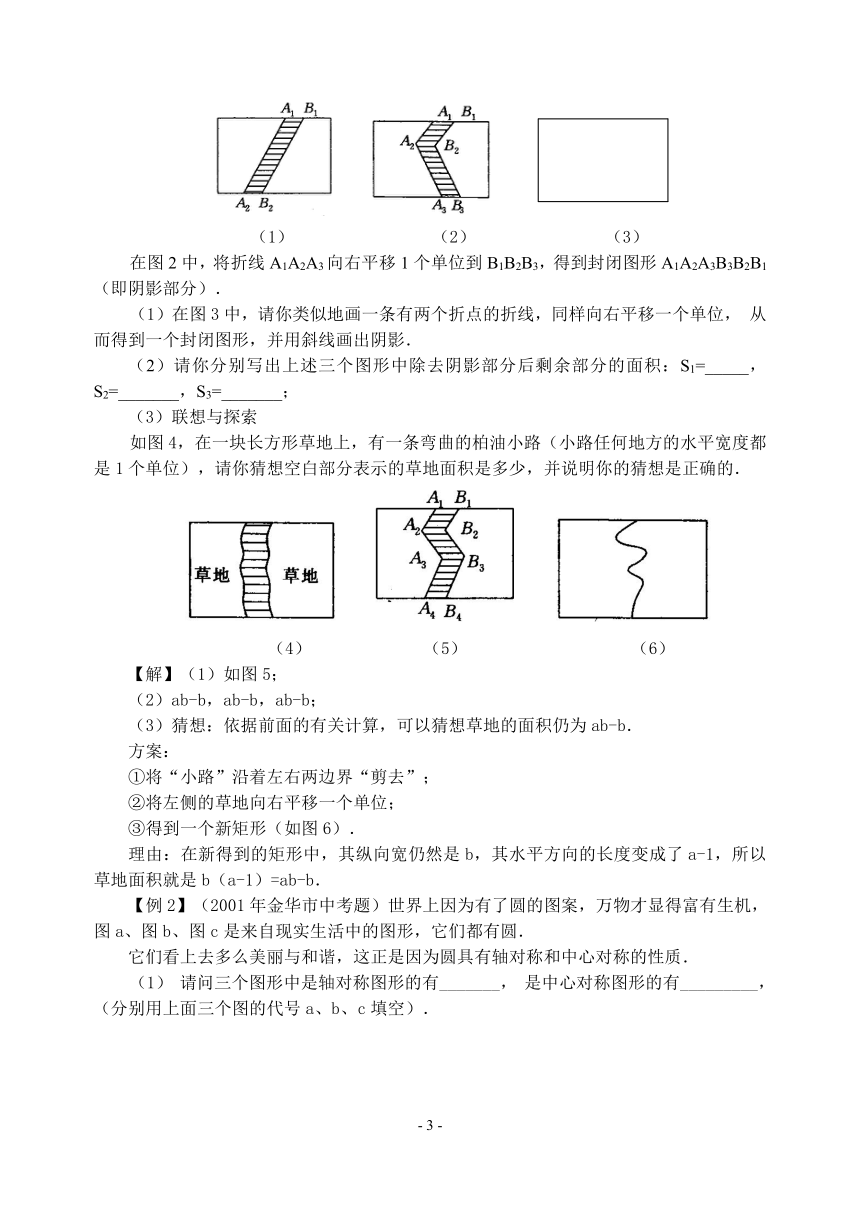
(1)在图3中,请你类似地画一条有两个折点的折线,同样向右平移一个单位,从而得到一个封闭图形,并用斜线画出阴影.
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:S1=_____,S2=_______,S3=_______;
(3)联想与探索
如图4,在一块长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少,并说明你的猜想是正确的.
(4) (5) (6)
【解】(1)如图5;
(2)ab-b,ab-b,ab-b;
(3)猜想:依据前面的有关计算,可以猜想草地的面积仍为ab-b.
方案:
①将“小路”沿着左右两边界“剪去”;
②将左侧的草地向右平移一个单位;
③得到一个新矩形(如图6).
理由:在新得到的矩形中,其纵向宽仍然是b,其水平方向的长度变成了a-1,所以草地面积就是b(a-1)=ab-b.
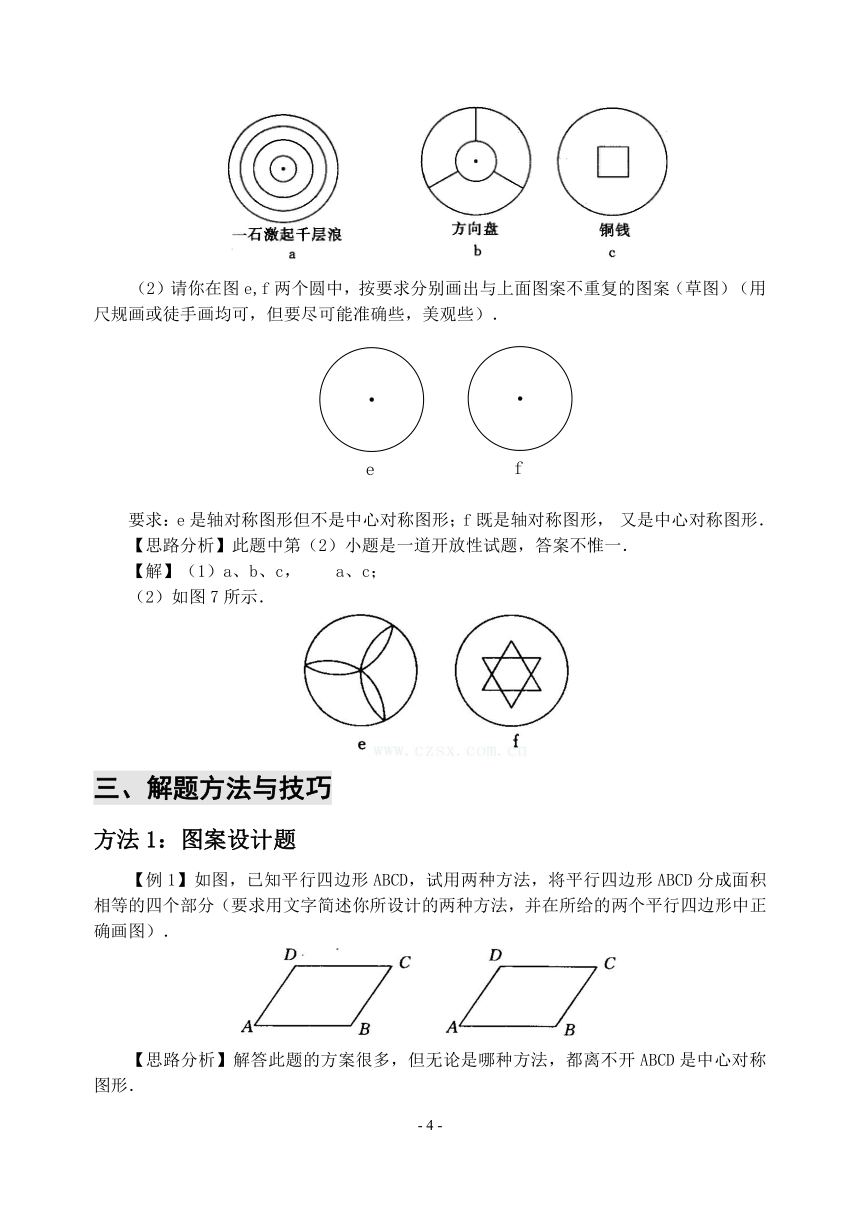
【例2】(2001年金华市中考题)世界上因为有了圆的图案,万物才显得富有生机,图a、图b、图c是来自现实生活中的图形,它们都有圆.
它们看上去多么美丽与和谐,这正是因为圆具有轴对称和中心对称的性质.
(1)请问三个图形中是轴对称图形的有_______,是中心对称图形的有_________,(分别用上面三个图的代号a、b、c填空).
(2)请你在图e,f两个圆中,按要求分别画出与上面图案不重复的图案(草图)(用尺规画或徒手画均可,但要尽可能准确些,美观些).
要求:e是轴对称图形但不是中心对称图形;f既是轴对称图形,又是中心对称图形.
【思路分析】此题中第(2)小题是一道开放性试题,答案不惟一.
【解】(1)a、b、c, a、c;
(2)如图7所示.
三、解题方法与技巧
方法1:图案设计题
【例1】如图,已知平行四边形ABCD,试用两种方法,将平行四边形ABCD分成面积相等的四个部分(要求用文字简述你所设计的两种方法,并在所给的两个平行四边形中正确画图).
【思路分析】解答此题的方案很多,但无论是哪种方法,都离不开ABCD是中心对称图形.
【解】如图所示(选择其中任意两种).
【例2】一位农夫临终前把他的四个儿子叫到床前说:“我没什么留给你们,只有祖上留下的几十亩地.我死后,你们把它分了吧,为了避免争吵,你们还是平分吧.”农夫死后,他的四个儿子开始分地,地里有四口井,4棵树,如图,他们决定分成面积,形状相同的四块,并且每人一口井,一棵树,但他们左比比,右画画,不知怎么分.同学们,你能帮帮他们吗?
【解】如图.
【例3】如图,田村有一口呈四边形的池塘,在它的四角A、B、C、D处均种有一棵大核桃树.田村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持核桃树不动,并要求扩建后的池塘成平行四边形形状,请问田村能否实现这一设想?若能,请你设计并画出图形;若不能,请说明理由(画图要保留痕迹,不写画法.)
【分析】此题考查的是中心对称(或旋转)的应用.连结AC、BD相交于O,将△ABO、△BCO、△CDO、△DAO分别绕AB、BC、CD、DA的中点旋转180°,拼成一个平行四边形.
【解】能,设计如图所示.
方法2:利用旋转变换解决几何问题
【例4】如图,有边长为1的等边三角形ABC和顶角为120°的等腰△DBC,以D为顶点作60°角,两边分别交AB、AC于M、N的三角形,连结MN,试说明△AMN的周长为2.
【思路分析】把△NDC绕点D逆时针方向旋转120°,得到△N′DB.由条件可知∠ABD=∠ACD=90°.
∴A、B、N′共线
∵DN′=DN ∠MDN=60° ∠2+∠3=60°
∴∠1=∠2
∴∠1+∠3=60°=∠MDN ∵MD=MD
∴△MDN′与△MDN关于MD对称
∴MN=MN′ 问题可求.
【解】如图,将△DNC绕D点旋转,使点C与点B重合,得到△DN′B,∵△ABC为等边三角形,所以∠ABC=∠ACB=60°,又∵△DBC是顶角为120°的等腰三角形,所以∠DBC=∠DCB=30°,∴∠ACD=∠ABD=∠DBN′=90°,DM=DM,DN=DN′,∠MDN=∠DMN′=60°,所以△DMN与△DMN′关于DM对称,故MN=MN′=BM+CN,所以△AMN的周长=AM+NA+MN=AM+AN+BM+CN=AB+AC=2.
四、中考试题归类解析
(一)图形平移
【例1】(2004,安徽)如图,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是( )
A.△OCD B.△OAB C.△OAF D.△OEF
【思路分析】按平移的定义进行判断且利用平移的性质进行验证.
【解】答案:选C
【规律总结】1.△ODE也可以由△OBC平移得到.2.要记住平移的性质.
(二)图形旋转
【例1】(2004,淄博)在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转,下列图案中,不能由一个图形通过旋转而构成的是( )
【思路分析】利用图形旋转的定义进行判断就可判断出来.
【解】答案:选C
【规律总结】图形旋转的性质可以帮助确定是否是旋转.
五、中考试题集萃
(一)填空题
1.(2003,河南)把正方形ABCD沿着对角线AC的方向移动到正方形A′B′C′D′的位置,它们的重叠部分(如图1中的阴影部分)的面积是正方形ABCD面积的一半,若AC=,则正方形移动的距离是AA′是_______.
(1) (2) (3)
2.(2004,南宁)如图2是两张全等的图案,它们完全重合在叠放在一起按住下面的图案不动,将上面图案绕点O顺时针旋转,至少旋转_______度角后,两张图案构成的图形是中心对称图形.
(二)选择题
1.(2003,陕西)香港于1997年7月1日成为中华人民共和国的一个特别行政区,它的区徽图案(紫荆花)如图3,这个图形( )
A.是轴对称图形; B.是中心对称图形
C.既是轴对称图形,也是中心对称图形;D.既不是轴对称图形,也不是中心对称图形
2.(2004,济南)在综合实践活动课上,小红准备用两种不同颜色的布料缝制一个正方形坐垫,坐垫的图案如图所示,应该选下图中的哪一块布料才能使其与原图拼接符合原来的图案模式( )
3.(2004,济南)一电动玩具的正面是由半径为10cm的小圆盘和半径为20cm的大圆盘依图中方式连接而成的,小圆盘在大圆盘的圆周上外切滚动一周且不发生滑动(大圆盘不动).回到原来的位置,在这一过程中,判断虚线所示位置的三个圆内,所画的头发,眼睛,嘴巴位置正确的是(不妨动手试一试!)( )
4.(2004,海口)观察下面的图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是( )
(三)解答题
1.(2004,甘肃)某产品的标志图案如图1所示,要在所给的图2中,把A、B、C三个菱形通过一种或几种变换,使之变为与图1一样的图案.
(1)请你在图2中作出变换后的图案(最终图案用实线表示)
(2)你所用的变换方示是_________.(在以下变换方法中,选择一种正确的填到横线上,也可以用自己的话表述)
①将菱形B向上平移.
②将菱形B绕点O旋转120°.
③将菱形B绕点O旋转180°.
2.(2004,宁安)如图,在10×5的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移4个单位,得到△A′B′C′,再把△A′B′C′绕点A′逆时针旋转90°,得到△A′B″C″.请你画出△A′B′C′和△A′B″C″(不要求写画法).
答案:
一、填空题:1.-1 2.60
二、选择题:1.D 2.C 3.B 4.C
三、解答题:
1.选①或③或其他正确方法
2.如图所示,正确画出△A′B′C′,正确画出△A′B″C″
- 1 -
一、基础知识梳理
1.平移的定义与规律
(1)定义:在平面内将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
关键:平移不改变图形的形状和大小,也不会改变图形的方向.
(2)平移的规律:经过平移,对应线段、对应角分别相等,对应点所连的线段平行且相等(或共线且相等).
(3)简单作图
平移的作图主要关注要点:1.方向,2.距离.整个平移的作图,就象把整个图案的每个特征点放在一套平行的轨道上滑动一样,每个特征点滑过的距离是一样的.
2.旋转的定义与规律
(1)定义:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.
关键:旋转不改变图形的大小和形状,但改变图形的方向.
(2)旋转的规律
经过旋转,图形上的每一点,都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.
(3)简单的旋转作图
旋转作图关键有两点:①旋转方向,②旋转角度.主要分四步:边、转、截、连.旋转就象把每个特征点与旋转中心用线连住的风筝,每个点转的角度是相同的,每个点与旋转中心的距离是不会改变的,即对应点与旋转中心距离相等.
3.图案的分析与设计
首先找到图中的基本图案,然后分析其图案与它的关系,即由它作何种运动变换而形成的,我们主要遇到的变换有:轴对称、平移、旋转.在相似形一章里还会学到图形的放大与缩小等.
二、考点与命题趋向分析
(一)能力
1.图形的平移
(1)通过具体实例认识平移,探索它的基本性质,理解对应点连线平行且相等的性质.
(2)能按要求作出简单平面图形平移后的图形.
(3)利用平移进行图案设计,认识和欣赏平移在现实生活中的应用.
2.图形的旋转.
(1)通过具体实例认识旋转,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质.
(2)了解平行四边形、圆是中心对称图形.
(3)能够按要求作出简单平面图形旋转后的图形.
(4)欣赏旋转在现实生活中的应用.
(5)探索图形之间的变换关系(轴对称、平移、旋转及其组合).
【例1】请说出下面乙树是怎样由甲树变换得到的.
【解】乙树是甲树先绕点A逆时针方向旋转到与地面垂直,然后再关于图中虚线(对称轴)轴对称得到的.
【例2】观察下面的图案,它可以看成是由哪个图形经过怎样的变换产生的?
【解】本图是由基本图形 旋转90°,连续旋转3次得到.
(6)灵活运用轴对称、平移和旋转的组合进行图案设计.
(二)命题趋向分析
近几年来,利用图形的平移出中考题在各省市屡见不鲜,有些题动手动脑程度很高,要求学生动手操作能力强.能够猜想、验证题目的结论,探索用平移变换解决比较复杂的问题.
值得注意的是新课标把平移与旋转引入新课程,又增加了图案设计内容,本章内容将成为今后几年中考命题的热点之一.
【例1】(2002年河北省)请你完成下列问题.
图形的操作过程(本题中四个长方形的水平方向的边长均为a,竖直方向的边长均为b);
在图1中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分);
(1) (2) (3)
在图2中,将折线A1A2A3向右平移1个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图3中,请你类似地画一条有两个折点的折线,同样向右平移一个单位,从而得到一个封闭图形,并用斜线画出阴影.
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:S1=_____,S2=_______,S3=_______;
(3)联想与探索
如图4,在一块长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少,并说明你的猜想是正确的.
(4) (5) (6)
【解】(1)如图5;
(2)ab-b,ab-b,ab-b;
(3)猜想:依据前面的有关计算,可以猜想草地的面积仍为ab-b.
方案:
①将“小路”沿着左右两边界“剪去”;
②将左侧的草地向右平移一个单位;
③得到一个新矩形(如图6).
理由:在新得到的矩形中,其纵向宽仍然是b,其水平方向的长度变成了a-1,所以草地面积就是b(a-1)=ab-b.
【例2】(2001年金华市中考题)世界上因为有了圆的图案,万物才显得富有生机,图a、图b、图c是来自现实生活中的图形,它们都有圆.
它们看上去多么美丽与和谐,这正是因为圆具有轴对称和中心对称的性质.
(1)请问三个图形中是轴对称图形的有_______,是中心对称图形的有_________,(分别用上面三个图的代号a、b、c填空).
(2)请你在图e,f两个圆中,按要求分别画出与上面图案不重复的图案(草图)(用尺规画或徒手画均可,但要尽可能准确些,美观些).
要求:e是轴对称图形但不是中心对称图形;f既是轴对称图形,又是中心对称图形.
【思路分析】此题中第(2)小题是一道开放性试题,答案不惟一.
【解】(1)a、b、c, a、c;
(2)如图7所示.
三、解题方法与技巧
方法1:图案设计题
【例1】如图,已知平行四边形ABCD,试用两种方法,将平行四边形ABCD分成面积相等的四个部分(要求用文字简述你所设计的两种方法,并在所给的两个平行四边形中正确画图).
【思路分析】解答此题的方案很多,但无论是哪种方法,都离不开ABCD是中心对称图形.
【解】如图所示(选择其中任意两种).
【例2】一位农夫临终前把他的四个儿子叫到床前说:“我没什么留给你们,只有祖上留下的几十亩地.我死后,你们把它分了吧,为了避免争吵,你们还是平分吧.”农夫死后,他的四个儿子开始分地,地里有四口井,4棵树,如图,他们决定分成面积,形状相同的四块,并且每人一口井,一棵树,但他们左比比,右画画,不知怎么分.同学们,你能帮帮他们吗?
【解】如图.
【例3】如图,田村有一口呈四边形的池塘,在它的四角A、B、C、D处均种有一棵大核桃树.田村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持核桃树不动,并要求扩建后的池塘成平行四边形形状,请问田村能否实现这一设想?若能,请你设计并画出图形;若不能,请说明理由(画图要保留痕迹,不写画法.)
【分析】此题考查的是中心对称(或旋转)的应用.连结AC、BD相交于O,将△ABO、△BCO、△CDO、△DAO分别绕AB、BC、CD、DA的中点旋转180°,拼成一个平行四边形.
【解】能,设计如图所示.
方法2:利用旋转变换解决几何问题
【例4】如图,有边长为1的等边三角形ABC和顶角为120°的等腰△DBC,以D为顶点作60°角,两边分别交AB、AC于M、N的三角形,连结MN,试说明△AMN的周长为2.
【思路分析】把△NDC绕点D逆时针方向旋转120°,得到△N′DB.由条件可知∠ABD=∠ACD=90°.
∴A、B、N′共线
∵DN′=DN ∠MDN=60° ∠2+∠3=60°
∴∠1=∠2
∴∠1+∠3=60°=∠MDN ∵MD=MD
∴△MDN′与△MDN关于MD对称
∴MN=MN′ 问题可求.
【解】如图,将△DNC绕D点旋转,使点C与点B重合,得到△DN′B,∵△ABC为等边三角形,所以∠ABC=∠ACB=60°,又∵△DBC是顶角为120°的等腰三角形,所以∠DBC=∠DCB=30°,∴∠ACD=∠ABD=∠DBN′=90°,DM=DM,DN=DN′,∠MDN=∠DMN′=60°,所以△DMN与△DMN′关于DM对称,故MN=MN′=BM+CN,所以△AMN的周长=AM+NA+MN=AM+AN+BM+CN=AB+AC=2.
四、中考试题归类解析
(一)图形平移
【例1】(2004,安徽)如图,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是( )
A.△OCD B.△OAB C.△OAF D.△OEF
【思路分析】按平移的定义进行判断且利用平移的性质进行验证.
【解】答案:选C
【规律总结】1.△ODE也可以由△OBC平移得到.2.要记住平移的性质.
(二)图形旋转
【例1】(2004,淄博)在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转,下列图案中,不能由一个图形通过旋转而构成的是( )
【思路分析】利用图形旋转的定义进行判断就可判断出来.
【解】答案:选C
【规律总结】图形旋转的性质可以帮助确定是否是旋转.
五、中考试题集萃
(一)填空题
1.(2003,河南)把正方形ABCD沿着对角线AC的方向移动到正方形A′B′C′D′的位置,它们的重叠部分(如图1中的阴影部分)的面积是正方形ABCD面积的一半,若AC=,则正方形移动的距离是AA′是_______.
(1) (2) (3)
2.(2004,南宁)如图2是两张全等的图案,它们完全重合在叠放在一起按住下面的图案不动,将上面图案绕点O顺时针旋转,至少旋转_______度角后,两张图案构成的图形是中心对称图形.
(二)选择题
1.(2003,陕西)香港于1997年7月1日成为中华人民共和国的一个特别行政区,它的区徽图案(紫荆花)如图3,这个图形( )
A.是轴对称图形; B.是中心对称图形
C.既是轴对称图形,也是中心对称图形;D.既不是轴对称图形,也不是中心对称图形
2.(2004,济南)在综合实践活动课上,小红准备用两种不同颜色的布料缝制一个正方形坐垫,坐垫的图案如图所示,应该选下图中的哪一块布料才能使其与原图拼接符合原来的图案模式( )
3.(2004,济南)一电动玩具的正面是由半径为10cm的小圆盘和半径为20cm的大圆盘依图中方式连接而成的,小圆盘在大圆盘的圆周上外切滚动一周且不发生滑动(大圆盘不动).回到原来的位置,在这一过程中,判断虚线所示位置的三个圆内,所画的头发,眼睛,嘴巴位置正确的是(不妨动手试一试!)( )
4.(2004,海口)观察下面的图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是( )
(三)解答题
1.(2004,甘肃)某产品的标志图案如图1所示,要在所给的图2中,把A、B、C三个菱形通过一种或几种变换,使之变为与图1一样的图案.
(1)请你在图2中作出变换后的图案(最终图案用实线表示)
(2)你所用的变换方示是_________.(在以下变换方法中,选择一种正确的填到横线上,也可以用自己的话表述)
①将菱形B向上平移.
②将菱形B绕点O旋转120°.
③将菱形B绕点O旋转180°.
2.(2004,宁安)如图,在10×5的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移4个单位,得到△A′B′C′,再把△A′B′C′绕点A′逆时针旋转90°,得到△A′B″C″.请你画出△A′B′C′和△A′B″C″(不要求写画法).
答案:
一、填空题:1.-1 2.60
二、选择题:1.D 2.C 3.B 4.C
三、解答题:
1.选①或③或其他正确方法
2.如图所示,正确画出△A′B′C′,正确画出△A′B″C″
- 1 -
