高一下学期物理人教版(2019版)必修二 第七章 万有引力与宇宙航行 单元检测(A卷)(含解析)
文档属性
| 名称 | 高一下学期物理人教版(2019版)必修二 第七章 万有引力与宇宙航行 单元检测(A卷)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-18 11:58:26 | ||
图片预览




文档简介
第七章 万有引力与宇宙航行 单元检测(A卷)
一、单选题
1.已知甲、乙两行星的半径之比为a,它们各自的第一宇宙速度之比为b,则下列结论不正确的是( )
A.甲、乙两行星的质量之比为b2a:1
B.甲、乙两行星表面的重力加速度之比为b2:a
C.甲、乙两行星各自卫星的最小周期之比为a:b
D.甲、乙两行星各自卫星的最大角速度之比为a:b
2.关于地球的第一宇宙速度,下面说法中错误的是
A.它是人造地球卫星绕地球飞行的最小速度
B.它是绕地球做圆周运动的人造地球卫星的最大运行速度
C.它是在近地圆形轨道上运行的人造地球卫星的运行速度
D.它是在地面上发射人造地球卫星所需要的最小发射速度
3.如图所示,三个质量均为M的球分别位于圆环、半圆环和完整圆环的圆心, 圆环、半圆环分别是由与丙图中相同的完整圆环截去和一半所得,环的粗细忽略不计,若甲图中环对球的万有引力大小为F, 则乙图、丙图中环对球的万有引力大小分别为( )
A.F,2F B.F,0
C.F,2F D.F,F
4.下图中的四种虚线轨迹,不可能是人造地球卫星轨道的是( )
A. B. C. D.
5.2022年左右我国将建成载人空间站,轨道高度距地面约,在轨运营10年以上,它将成为中国空间科学和新技术研究实验的重要基地。设该空间站绕地球做匀速圆周运动,其运动周期为,轨道半径为,万有引力常量为,地球半径为,地球表面重力加速度为。下列说法不正确的是( )
A.地球的质量为
B.空间站的线速度大小为
C.空间站的向心加速度为
D.空间站的运行周期小于地球自转周期
6.在水平路面上做匀速直线运动的小车上有一固定的竖直杆,车上的三个水平支架上有三个完全相同的小球A、B、C,它们离地面的高度分别为3h、2h和h,当小车遇到障碍物P时,立即停下来,三个小球同时从支架上水平抛出,先后落到水平路面上,如图所示,不计空气阻力,则下列说法正确的是( )
A.三个小球落地时间差与车速有关
B.三个小球落地点的间隔距离L1=L2
C.三个小球落地点的间隔距离L1D.三个小球落地点的间隔距离L1>L2
7.2016年2月11日,美国自然科学基金召开新闻发布会宣布,人类首次探测到了引力波。2月16日,中国科学院公布了一项新的探测引力波的“空间太极计划”,其中,由中山大学发起的空间引力波探测工程“天琴计划”于15年7月正式启动。计划从2016年到2035年分四阶段进行,将向太空发射三颗卫星探测引力波。在目前讨论的初步概念中,天琴将采用三颗完全相同的卫星构成一个等边三角形阵列,地球恰处于三角形中心,卫星将在以地球为中心、高度约10万千米的轨道上运行,针对确定的引力波源进行探测,这三颗卫星在太空中的分列图类似乐器竖琴,故命名为“天琴计划”。则下列有关这三颗卫星的运动描述正确的是( )
A.三颗卫星一定是地球同步卫星
B.三颗卫星具有相同大小的加速度
C.三颗卫星的线速度比月球绕地球运动的线速度大且大于第一宇宙速度
D.若知道引力常量及三颗卫星绕地球运转的周期可估算出地球的密度
8.过去几千年来,人类对行星的认识与研究仅限于太阳系内,行星“51 peg b”的发现拉开了研究太阳系外行星的序幕.“51 peg b”绕其中心恒星做匀速圆周运动,周期约为4天,轨道半径约为地球绕太阳运动半径为1/20,该中心恒星与太阳的质量比约为( )
A.1/10 B.1 C.5 D.10
二、多选题
9.探月工程中,“嫦娥三号”探测器的发射过程可以简化如下:卫星由地面发射后,进入地月转移轨道,经过P点时变轨进入距离月球表面100公里的圆形轨道1,在轨道1上经过Q点时变轨进入椭圆轨道2,轨道2与月球表面相切于M点,月球车将在M点着陆月球。下列说法正确的是( )
A.“嫦娥三号”在轨道1上的速度比月球的第一宇宙速度小
B.“嫦娥三号”在地月转移轨道上经过P点的速度比在轨道1上经过P点时大
C.“嫦娥三号”在轨道1上的运动周期比在轨道2上的小
D.“嫦娥三号”在轨道1上经过Q点时的加速度小于在轨道2上经过Q点时的加速度
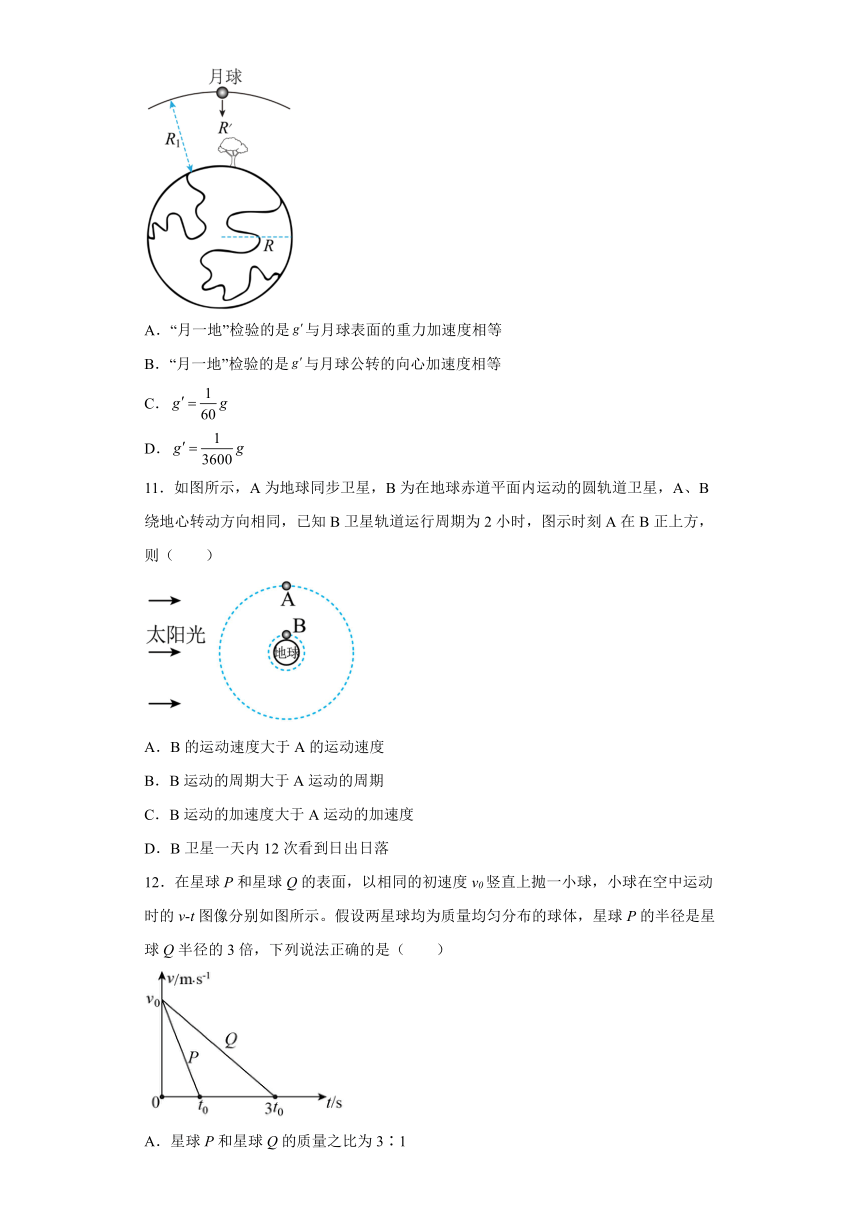
10.图为牛顿“月一地”检验示意图,已知月球公转的轨道半径为地球半径的60倍,轨道处的重力加速度为,地球表面的月球重力加速度为,则( )
A.“月一地”检验的是与月球表面的重力加速度相等
B.“月一地”检验的是与月球公转的向心加速度相等
C.
D.
11.如图所示,A为地球同步卫星,B为在地球赤道平面内运动的圆轨道卫星,A、B绕地心转动方向相同,已知B卫星轨道运行周期为2小时,图示时刻A在B正上方,则( )
A.B的运动速度大于A的运动速度
B.B运动的周期大于A运动的周期
C.B运动的加速度大于A运动的加速度
D.B卫星一天内12次看到日出日落
12.在星球P和星球Q的表面,以相同的初速度v0竖直上抛一小球,小球在空中运动时的v-t图像分别如图所示。假设两星球均为质量均匀分布的球体,星球P的半径是星球Q半径的3倍,下列说法正确的是( )
A.星球P和星球Q的质量之比为3∶1
B.星球P和星球Q的密度之比为1:1
C.星球P和星球Q的第一宇宙速度之比为3∶1
D.星球P和星球Q的近地卫星周期之比为1∶3
三、实验题
13.一艘宇宙飞船飞近某一新发现的行星,并进入靠近该行星表面的圆形轨道绕行数圈后,着陆在行星上,宇宙飞船上备有以下实验仪器:
A.弹簧测力计一个
B.精确秒表一只
C.天平一台(附砝码一套)
D.物体一个
为测定该行星的质量M和半径R,宇航员在绕行及着陆后各进行一次测量,依据测量数据可以求出M和R(已知引力常量为G)。
(1)绕行时测量所用的仪器为________(用仪器的字母序号表示),所测物理量为________。
(2)着陆后测量所用的仪器为________(用仪器的字母序号表示),所测物理量为______________________。用测量数据求该行星质量M=________,用测量数据求该星球半径R=________。
14.某物理小组的同学设计了一个粗制玩具小车通过凹形桥最低点时的速度的实验.所用器材有:玩具小车、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为R=0.20m).
完成下列填空:
(1)将凹形桥模拟器静置于托盘秤上,如图(a)所示,托盘秤的示数为1.00kg;
(2)将玩具小车静置于凹形桥模拟器最低点时,托盘秤的示数如图(b)所示,该示数为_____kg;
(3)将小车从凹形桥模拟器某一位置释放,小车经过最低点后滑向另一侧,此过程中托盘秤的最大示数为m;多次从同一位置释放小车,记录各次的m值如下表所示:
序号 1 2 3 4 5
m(kg) 1.80 1.75 1.85 1.75 1.90
(4)根据以上数据,可求出小车经过凹形桥最低点时对桥的压力为_____N;小车通过最低点时的速度大小为_______m/s.(重力加速度大小取9.80m/s2 ,计算结果保留2位有效数字)
四、解答题
15.载人飞船的舱中有一体重计,体重计上放一物体,火箭点火前,宇航员观察到体重计的示数为。在载人飞船随火箭竖直向上匀加速升空的过程中,当飞船离地面高度为H时,宇航员观察到体重计示数为F。设地球半径为R,第一宇宙速度为,求:
(1)该物体的质量;
(2)火箭上升的加速度。
16.如图所示是月亮女神、嫦娥号绕月亮做圆周运动时某时刻的图片,用、、、分别表示月亮女神和嫦娥号的轨道半径及周期,用表示月亮的半径.
()请用万有引力知识证明:它们遵循,其中是只与月球质量有关而与卫星无关的常量;
()再经多少时间两卫星第一次相距最远;
()请用嫦娥号所给的已知量,估测月球的平均密度.
17.天文学家测得银河系中氦的含量约为,有关研究表明,宇宙中氦生成的途径有两条,一是在宇宙诞生后3分钟左右生成的,二是在宇宙演化到恒星诞生后,由恒星内部氢核聚变反应生成的。
(1)把氢核聚变反应简化为4个氢核聚变成氦核,同时放出2个正电子和2个中微子。请写出该氢核聚变反应的方程式,并计算一次反应释放的能量(计算结果用焦耳表示,取两位有效数字);
(2)研究表明,银河系的年龄为,每秒钟银河系产生的能量约为,现假定该能量全部来自上述氢核聚变反应。试估算银河系中由上述氢核聚变所产生的氦的质量,计算结果保留一位有效数字;
(3)根据你的估算结果,对银河系中氦的主要生成途径作出判断。(可能用到的数据:银河系质量为,原子质量单位,1u相当于的能量,电子质量,氦核质量,氢核质量,中微子质量为零,阿伏加德罗常数)
18.由于地球的自转,物体在地球上不同纬度处随地球自转所需向心力的大小不同,因此同一个物体在地球上不同纬度处重力大小也不同,在地球赤道上的物体受到的重力与其在地球两极点受到的重力大小之比约为299:300,因此我们通常忽略两者的差异,可认为两者相等.而有些星球,却不能忽略.假如某星球因为自转的原因,一物体在赤道上的重力与其在该星球两极点受到的重力大小之比为7:8,已知该星球的半径为R,求:
(1)绕该星球运动的同步卫星的轨道半径r;
(2)若已知该星球赤道上的重力加速度大小为g,万有引力常量为G,则该星球的密度ρ.
参考答案:
1.D
【详解】B.由
可得第一宇宙速度为
则行星表面的重力加速度为
由于甲、乙两行星的半径之比为a、各自的第一宇宙速度之比为b,故甲乙两行星的表面重力加速度之比为b2:a,B正确;
A.由
得
则由半径之比为a、重力加速度之比为b2:a,可得甲乙两行星的质量之比为b2a:1,故A正确;
C.由
得
可知轨道半径越小,周期越小,故最小周期
结合甲乙两行星的质量之比为b2a:1、半径之比为a,可得最小周期之比为a:b,故C正确;
D.根据
可知轨道半径越小,角速度最大,由于最小周期之比为a:b,则最大角速度之比为b:a,故D错误。
本题选不正确的,故选D。
2.A
【详解】卫星在圆轨道上运行时,速度为 ,轨道半径越大,速度越小,故第一宇宙速度是卫星在圆轨道上运行的最大速度,故A错误,选项B正确;物体在地面附近绕地球做匀速圆周运动的速度叫做第一宇宙速度,在地面附近发射飞行器,如果速度等于,飞行器恰好做匀速圆周运动,如果速度小于,就出现万有引力大于飞行器做圆周运动所需的向心力,做近心运动而落地,所以发射速度不能小于,即它是发射人造地球卫星所需的最小地面发射速度,故选项C、D正确
3.B
【详解】将甲图圆环看成是三个圆环的组合,关于圆心对称的两个圆环对球的万有引力的合力为零,由题知 圆环对球的万有引力大小为F,所以圆环对球的万有引力大小为F;将乙图半圆环看成是两个圆环的组合,根据平行四边形定则,乙图半圆环对球的万有引力大小为F,方向向上;将丙图完整圆环看成是4个圆环的组合,关于圆心对称的两个圆环对球的万有引力的合力为零,因此丙图整个圆环对球的引力为0。故选B。
【点睛】分析清甲图圆环的结构特点是本题的突破口。利用对称思想,推断出甲图中左上方圆环对球的万有引力大小为F,再将乙、丙中的圆环看成由几个圆环组成,利用矢量合成及对称法轻松解题。
4.B
【详解】人造地球卫星靠地球的万有引力提供向心力而绕地球做匀速圆周运动,地球对卫星的万有引力方向指向地心,所以人造地球卫星做圆周运动的圆心是地心,否则不能做稳定的圆周运动。故B不可能,ACD可能。
故选B。
5.B
【详解】A. 由万有引力等于向心力,可得
故A正确,不符合题意;
BC.由在地表
空间站
联立可得
故B错误,符合题意,C正确,不符合题意;
D.因为空间站轨道半径小于同步卫星轨道半径,根据开普勒第三定律可知,空间站的运行周期小于地球自转周期,故D正确,不符合题意。
故选B。
6.C
【详解】试题分析:据题意三个小球从车上水平抛出后均做平抛运动,平抛运动的时间与高度有关,所以A选项错误;据h=gt2,三个小球的落地时间比为tA:tB:tC=,又据L=vt,小球落地间隔距离之比为:L1:L2=(- ):(-1)<1,说明L1考点:本题考查对平抛运动的应用.
7.B
【详解】A.地球的同步卫星,必须在地球的赤道平面上,且距离地球的高度为左右,故此三颗卫星不可能是地球的同步卫星,故A错误;
B.因三颗卫星均以地球为中心,在高度约10万千米的轨道上运行,根据可知,三颗卫星具有相同大小的加速度,故B正确;
C.三颗卫星距离地球的距离比月球到地球的距离小得多,根据
得
可知,三颗卫星的线速度比月球绕地球运动的线速度大且小于第一宇宙速度,故C错误;
D.若知道引力常量及三颗卫星绕地球运转的周期T,根据
可解得
但因地球的半径未知,故不能估算出地球的密度,故D错误。
故选B。
8.B
【详解】研究行星绕某一恒星做匀速圆周运动,根据万有引力提供向心力,列出等式为:
,解得; “51 peg b”绕其中心恒星做匀速圆周运动,周期约为4天,轨道半径约为地球绕太阳运动半径的1/20,所以该中心恒星与太阳的质量比约为 ,故选B.
点睛:要求解一个物理量大小变化,我们应该把这个物理量先表示出来,再根据已知量进行判断.向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.
9.AB
【详解】A.月球的第一宇宙速度是卫星贴近月球表面做匀速圆周运动的速度,“嫦娥三号”在轨道1上的半径大于月球半径,根据
得线速度
可知“嫦娥三号”在轨道1上的运动速度比月球的第一宇宙速度小,A正确;
B.“嫦娥三号”在地月转移轨道上经过P点若要进入轨道1,需减速,所以在地月转移轨道上经过P点的速度比在轨道1上经过P点时大,B正确;
C.根据开普勒第三定律得卫星在轨道2上运动轨道的半长轴比在轨道1上轨道半径小,所以卫星在轨道1上运动周期比在轨道2上大,C错误;
D.“嫦娥三号”无论在哪个轨道上经过Q点时的加速度都为该点的万有引力加速度,因为都是Q点可知,万有引力在此产生的加速度相等,D错误。
故选AB。
10.BD
【详解】AB.假设地面的地球吸引力与地球吸引月球绕地球运行的引力是同种力,遵循相同的规律,已知月球公转的轨道半径为地球半径的60倍,那么应该比较的是月球绕地球运行的向心加速度与地面的重力加速度的比值,即“月-地”检验的是与月球公转的向心加速度相等,故A错误,B正确;
CD.根据“月-地”检验的原理可知,月球绕地球运行轨道半径是地球半径的60倍,月球轨道上一个物体的受到的引力与它在地面附近时受到的引力之比为月球在轨道处的重力加速度与地球表面的重力加速度的关系为
故C错误,D正确;
故选BD。
11.ACD
【详解】B.由于A为地球同步卫星,周期为
所以B运动的周期小于A运动的周期,根据开普勒第三定律可得B运动的轨道半径小于A运动的轨道半径,故B错误;
A.根据
可得
所以B的运动速度大于A的运动速度,故A正确;
C.根据
可得
所以B的运动加速度大于A的运动加速度,故C正确;
D.由于B卫星轨道运行周期为2小时,是地球自转周期的,B卫星一天内12次看到日出日落,故D正确。
故选ACD。
12.BC
【详解】根据v-t图像的斜率表示加速度,可是两星球表面重力加速度之比为
A.根据
可得
得到,故A错误;
B.由
联立可得
得到,故B正确;
C.由
联立上面式子得到
得出星球P和星球Q的第一宇宙速度之比为,故C正确;
D.由
可得
得出,故D错误。
故选BC。
13. B 周期T ACD 物体质量m、重力F
【详解】[1][2][3][4]根据
=mg
=m2R
设用秒表测得绕行星表面运动一周的时间即周期为T,用天平测得物体的质量为m,用测力计测得该物体的重力为F;
[5][6]则
g=
解得
R=
M=
14. 1.40 7.9 1.4
【详解】(1)[1]根据量程为10kg,最小分度为0.1kg,注意估读到最小分度的下一位,为1.40kg
(2)[2]根据表格知最低点小车和凹形桥模拟器中质量的平均值
解得
[3]根据牛顿运动定律知
代入数据解得
15.(1) ;(2)
【详解】(1)设地面附近重力加速度为,由火箭点火前体重计示数为可知,物体质量为
由第一宇宙速度公式
可得地球表面附近的重力加速度
联立解得该物体的质量为
(2)当飞船离地面高度为H时,物体所受万有引力为
而
对物体应用牛顿第二定律得
联立可得火箭上升的加速度
16.()见解析;();()
【详解】(1)设月球的质量为M,对任一卫星均有
得
常量.
(2)两卫星第一次相距最远时有
(3)对嫦娥1号有
M=πR3ρ
17.(1),;(2);(3)见解析
【详解】(1)由质量数与核电荷数守恒可知,核反应方程式为
核反应中的质量亏损
释放出的核能
(2)银河系的年龄为,每秒钟银河系产生的能量约为,则产生的总能量为,根据核反应释放的能量,计算核反应产生的氦的质量
(3)宇宙诞生之初,氦的含量
由估算结果可知,远小于的实际值,所以银河系中的氦主要是宇宙诞生后不久生成的。
18.(1)2R;(2)
【详解】(1)设物体质量为m,星球质量为M,星球的自转周期为T,物体在星球两极时,万有引力等于重力,即
物体在星球赤道上随星球自转时,向心力由万有引力的一个分力提供,另一个分力就是重力,有
因为
得
该星球的同步卫星的周期等于自转周期T,则有
联立解得
(2)在星球赤道上,有
可得
又因星球的体积
所以该星球的密度
一、单选题
1.已知甲、乙两行星的半径之比为a,它们各自的第一宇宙速度之比为b,则下列结论不正确的是( )
A.甲、乙两行星的质量之比为b2a:1
B.甲、乙两行星表面的重力加速度之比为b2:a
C.甲、乙两行星各自卫星的最小周期之比为a:b
D.甲、乙两行星各自卫星的最大角速度之比为a:b
2.关于地球的第一宇宙速度,下面说法中错误的是
A.它是人造地球卫星绕地球飞行的最小速度
B.它是绕地球做圆周运动的人造地球卫星的最大运行速度
C.它是在近地圆形轨道上运行的人造地球卫星的运行速度
D.它是在地面上发射人造地球卫星所需要的最小发射速度
3.如图所示,三个质量均为M的球分别位于圆环、半圆环和完整圆环的圆心, 圆环、半圆环分别是由与丙图中相同的完整圆环截去和一半所得,环的粗细忽略不计,若甲图中环对球的万有引力大小为F, 则乙图、丙图中环对球的万有引力大小分别为( )
A.F,2F B.F,0
C.F,2F D.F,F
4.下图中的四种虚线轨迹,不可能是人造地球卫星轨道的是( )
A. B. C. D.
5.2022年左右我国将建成载人空间站,轨道高度距地面约,在轨运营10年以上,它将成为中国空间科学和新技术研究实验的重要基地。设该空间站绕地球做匀速圆周运动,其运动周期为,轨道半径为,万有引力常量为,地球半径为,地球表面重力加速度为。下列说法不正确的是( )
A.地球的质量为
B.空间站的线速度大小为
C.空间站的向心加速度为
D.空间站的运行周期小于地球自转周期
6.在水平路面上做匀速直线运动的小车上有一固定的竖直杆,车上的三个水平支架上有三个完全相同的小球A、B、C,它们离地面的高度分别为3h、2h和h,当小车遇到障碍物P时,立即停下来,三个小球同时从支架上水平抛出,先后落到水平路面上,如图所示,不计空气阻力,则下列说法正确的是( )
A.三个小球落地时间差与车速有关
B.三个小球落地点的间隔距离L1=L2
C.三个小球落地点的间隔距离L1
7.2016年2月11日,美国自然科学基金召开新闻发布会宣布,人类首次探测到了引力波。2月16日,中国科学院公布了一项新的探测引力波的“空间太极计划”,其中,由中山大学发起的空间引力波探测工程“天琴计划”于15年7月正式启动。计划从2016年到2035年分四阶段进行,将向太空发射三颗卫星探测引力波。在目前讨论的初步概念中,天琴将采用三颗完全相同的卫星构成一个等边三角形阵列,地球恰处于三角形中心,卫星将在以地球为中心、高度约10万千米的轨道上运行,针对确定的引力波源进行探测,这三颗卫星在太空中的分列图类似乐器竖琴,故命名为“天琴计划”。则下列有关这三颗卫星的运动描述正确的是( )
A.三颗卫星一定是地球同步卫星
B.三颗卫星具有相同大小的加速度
C.三颗卫星的线速度比月球绕地球运动的线速度大且大于第一宇宙速度
D.若知道引力常量及三颗卫星绕地球运转的周期可估算出地球的密度
8.过去几千年来,人类对行星的认识与研究仅限于太阳系内,行星“51 peg b”的发现拉开了研究太阳系外行星的序幕.“51 peg b”绕其中心恒星做匀速圆周运动,周期约为4天,轨道半径约为地球绕太阳运动半径为1/20,该中心恒星与太阳的质量比约为( )
A.1/10 B.1 C.5 D.10
二、多选题
9.探月工程中,“嫦娥三号”探测器的发射过程可以简化如下:卫星由地面发射后,进入地月转移轨道,经过P点时变轨进入距离月球表面100公里的圆形轨道1,在轨道1上经过Q点时变轨进入椭圆轨道2,轨道2与月球表面相切于M点,月球车将在M点着陆月球。下列说法正确的是( )
A.“嫦娥三号”在轨道1上的速度比月球的第一宇宙速度小
B.“嫦娥三号”在地月转移轨道上经过P点的速度比在轨道1上经过P点时大
C.“嫦娥三号”在轨道1上的运动周期比在轨道2上的小
D.“嫦娥三号”在轨道1上经过Q点时的加速度小于在轨道2上经过Q点时的加速度
10.图为牛顿“月一地”检验示意图,已知月球公转的轨道半径为地球半径的60倍,轨道处的重力加速度为,地球表面的月球重力加速度为,则( )
A.“月一地”检验的是与月球表面的重力加速度相等
B.“月一地”检验的是与月球公转的向心加速度相等
C.
D.
11.如图所示,A为地球同步卫星,B为在地球赤道平面内运动的圆轨道卫星,A、B绕地心转动方向相同,已知B卫星轨道运行周期为2小时,图示时刻A在B正上方,则( )
A.B的运动速度大于A的运动速度
B.B运动的周期大于A运动的周期
C.B运动的加速度大于A运动的加速度
D.B卫星一天内12次看到日出日落
12.在星球P和星球Q的表面,以相同的初速度v0竖直上抛一小球,小球在空中运动时的v-t图像分别如图所示。假设两星球均为质量均匀分布的球体,星球P的半径是星球Q半径的3倍,下列说法正确的是( )
A.星球P和星球Q的质量之比为3∶1
B.星球P和星球Q的密度之比为1:1
C.星球P和星球Q的第一宇宙速度之比为3∶1
D.星球P和星球Q的近地卫星周期之比为1∶3
三、实验题
13.一艘宇宙飞船飞近某一新发现的行星,并进入靠近该行星表面的圆形轨道绕行数圈后,着陆在行星上,宇宙飞船上备有以下实验仪器:
A.弹簧测力计一个
B.精确秒表一只
C.天平一台(附砝码一套)
D.物体一个
为测定该行星的质量M和半径R,宇航员在绕行及着陆后各进行一次测量,依据测量数据可以求出M和R(已知引力常量为G)。
(1)绕行时测量所用的仪器为________(用仪器的字母序号表示),所测物理量为________。
(2)着陆后测量所用的仪器为________(用仪器的字母序号表示),所测物理量为______________________。用测量数据求该行星质量M=________,用测量数据求该星球半径R=________。
14.某物理小组的同学设计了一个粗制玩具小车通过凹形桥最低点时的速度的实验.所用器材有:玩具小车、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为R=0.20m).
完成下列填空:
(1)将凹形桥模拟器静置于托盘秤上,如图(a)所示,托盘秤的示数为1.00kg;
(2)将玩具小车静置于凹形桥模拟器最低点时,托盘秤的示数如图(b)所示,该示数为_____kg;
(3)将小车从凹形桥模拟器某一位置释放,小车经过最低点后滑向另一侧,此过程中托盘秤的最大示数为m;多次从同一位置释放小车,记录各次的m值如下表所示:
序号 1 2 3 4 5
m(kg) 1.80 1.75 1.85 1.75 1.90
(4)根据以上数据,可求出小车经过凹形桥最低点时对桥的压力为_____N;小车通过最低点时的速度大小为_______m/s.(重力加速度大小取9.80m/s2 ,计算结果保留2位有效数字)
四、解答题
15.载人飞船的舱中有一体重计,体重计上放一物体,火箭点火前,宇航员观察到体重计的示数为。在载人飞船随火箭竖直向上匀加速升空的过程中,当飞船离地面高度为H时,宇航员观察到体重计示数为F。设地球半径为R,第一宇宙速度为,求:
(1)该物体的质量;
(2)火箭上升的加速度。
16.如图所示是月亮女神、嫦娥号绕月亮做圆周运动时某时刻的图片,用、、、分别表示月亮女神和嫦娥号的轨道半径及周期,用表示月亮的半径.
()请用万有引力知识证明:它们遵循,其中是只与月球质量有关而与卫星无关的常量;
()再经多少时间两卫星第一次相距最远;
()请用嫦娥号所给的已知量,估测月球的平均密度.
17.天文学家测得银河系中氦的含量约为,有关研究表明,宇宙中氦生成的途径有两条,一是在宇宙诞生后3分钟左右生成的,二是在宇宙演化到恒星诞生后,由恒星内部氢核聚变反应生成的。
(1)把氢核聚变反应简化为4个氢核聚变成氦核,同时放出2个正电子和2个中微子。请写出该氢核聚变反应的方程式,并计算一次反应释放的能量(计算结果用焦耳表示,取两位有效数字);
(2)研究表明,银河系的年龄为,每秒钟银河系产生的能量约为,现假定该能量全部来自上述氢核聚变反应。试估算银河系中由上述氢核聚变所产生的氦的质量,计算结果保留一位有效数字;
(3)根据你的估算结果,对银河系中氦的主要生成途径作出判断。(可能用到的数据:银河系质量为,原子质量单位,1u相当于的能量,电子质量,氦核质量,氢核质量,中微子质量为零,阿伏加德罗常数)
18.由于地球的自转,物体在地球上不同纬度处随地球自转所需向心力的大小不同,因此同一个物体在地球上不同纬度处重力大小也不同,在地球赤道上的物体受到的重力与其在地球两极点受到的重力大小之比约为299:300,因此我们通常忽略两者的差异,可认为两者相等.而有些星球,却不能忽略.假如某星球因为自转的原因,一物体在赤道上的重力与其在该星球两极点受到的重力大小之比为7:8,已知该星球的半径为R,求:
(1)绕该星球运动的同步卫星的轨道半径r;
(2)若已知该星球赤道上的重力加速度大小为g,万有引力常量为G,则该星球的密度ρ.
参考答案:
1.D
【详解】B.由
可得第一宇宙速度为
则行星表面的重力加速度为
由于甲、乙两行星的半径之比为a、各自的第一宇宙速度之比为b,故甲乙两行星的表面重力加速度之比为b2:a,B正确;
A.由
得
则由半径之比为a、重力加速度之比为b2:a,可得甲乙两行星的质量之比为b2a:1,故A正确;
C.由
得
可知轨道半径越小,周期越小,故最小周期
结合甲乙两行星的质量之比为b2a:1、半径之比为a,可得最小周期之比为a:b,故C正确;
D.根据
可知轨道半径越小,角速度最大,由于最小周期之比为a:b,则最大角速度之比为b:a,故D错误。
本题选不正确的,故选D。
2.A
【详解】卫星在圆轨道上运行时,速度为 ,轨道半径越大,速度越小,故第一宇宙速度是卫星在圆轨道上运行的最大速度,故A错误,选项B正确;物体在地面附近绕地球做匀速圆周运动的速度叫做第一宇宙速度,在地面附近发射飞行器,如果速度等于,飞行器恰好做匀速圆周运动,如果速度小于,就出现万有引力大于飞行器做圆周运动所需的向心力,做近心运动而落地,所以发射速度不能小于,即它是发射人造地球卫星所需的最小地面发射速度,故选项C、D正确
3.B
【详解】将甲图圆环看成是三个圆环的组合,关于圆心对称的两个圆环对球的万有引力的合力为零,由题知 圆环对球的万有引力大小为F,所以圆环对球的万有引力大小为F;将乙图半圆环看成是两个圆环的组合,根据平行四边形定则,乙图半圆环对球的万有引力大小为F,方向向上;将丙图完整圆环看成是4个圆环的组合,关于圆心对称的两个圆环对球的万有引力的合力为零,因此丙图整个圆环对球的引力为0。故选B。
【点睛】分析清甲图圆环的结构特点是本题的突破口。利用对称思想,推断出甲图中左上方圆环对球的万有引力大小为F,再将乙、丙中的圆环看成由几个圆环组成,利用矢量合成及对称法轻松解题。
4.B
【详解】人造地球卫星靠地球的万有引力提供向心力而绕地球做匀速圆周运动,地球对卫星的万有引力方向指向地心,所以人造地球卫星做圆周运动的圆心是地心,否则不能做稳定的圆周运动。故B不可能,ACD可能。
故选B。
5.B
【详解】A. 由万有引力等于向心力,可得
故A正确,不符合题意;
BC.由在地表
空间站
联立可得
故B错误,符合题意,C正确,不符合题意;
D.因为空间站轨道半径小于同步卫星轨道半径,根据开普勒第三定律可知,空间站的运行周期小于地球自转周期,故D正确,不符合题意。
故选B。
6.C
【详解】试题分析:据题意三个小球从车上水平抛出后均做平抛运动,平抛运动的时间与高度有关,所以A选项错误;据h=gt2,三个小球的落地时间比为tA:tB:tC=,又据L=vt,小球落地间隔距离之比为:L1:L2=(- ):(-1)<1,说明L1
7.B
【详解】A.地球的同步卫星,必须在地球的赤道平面上,且距离地球的高度为左右,故此三颗卫星不可能是地球的同步卫星,故A错误;
B.因三颗卫星均以地球为中心,在高度约10万千米的轨道上运行,根据可知,三颗卫星具有相同大小的加速度,故B正确;
C.三颗卫星距离地球的距离比月球到地球的距离小得多,根据
得
可知,三颗卫星的线速度比月球绕地球运动的线速度大且小于第一宇宙速度,故C错误;
D.若知道引力常量及三颗卫星绕地球运转的周期T,根据
可解得
但因地球的半径未知,故不能估算出地球的密度,故D错误。
故选B。
8.B
【详解】研究行星绕某一恒星做匀速圆周运动,根据万有引力提供向心力,列出等式为:
,解得; “51 peg b”绕其中心恒星做匀速圆周运动,周期约为4天,轨道半径约为地球绕太阳运动半径的1/20,所以该中心恒星与太阳的质量比约为 ,故选B.
点睛:要求解一个物理量大小变化,我们应该把这个物理量先表示出来,再根据已知量进行判断.向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.
9.AB
【详解】A.月球的第一宇宙速度是卫星贴近月球表面做匀速圆周运动的速度,“嫦娥三号”在轨道1上的半径大于月球半径,根据
得线速度
可知“嫦娥三号”在轨道1上的运动速度比月球的第一宇宙速度小,A正确;
B.“嫦娥三号”在地月转移轨道上经过P点若要进入轨道1,需减速,所以在地月转移轨道上经过P点的速度比在轨道1上经过P点时大,B正确;
C.根据开普勒第三定律得卫星在轨道2上运动轨道的半长轴比在轨道1上轨道半径小,所以卫星在轨道1上运动周期比在轨道2上大,C错误;
D.“嫦娥三号”无论在哪个轨道上经过Q点时的加速度都为该点的万有引力加速度,因为都是Q点可知,万有引力在此产生的加速度相等,D错误。
故选AB。
10.BD
【详解】AB.假设地面的地球吸引力与地球吸引月球绕地球运行的引力是同种力,遵循相同的规律,已知月球公转的轨道半径为地球半径的60倍,那么应该比较的是月球绕地球运行的向心加速度与地面的重力加速度的比值,即“月-地”检验的是与月球公转的向心加速度相等,故A错误,B正确;
CD.根据“月-地”检验的原理可知,月球绕地球运行轨道半径是地球半径的60倍,月球轨道上一个物体的受到的引力与它在地面附近时受到的引力之比为月球在轨道处的重力加速度与地球表面的重力加速度的关系为
故C错误,D正确;
故选BD。
11.ACD
【详解】B.由于A为地球同步卫星,周期为
所以B运动的周期小于A运动的周期,根据开普勒第三定律可得B运动的轨道半径小于A运动的轨道半径,故B错误;
A.根据
可得
所以B的运动速度大于A的运动速度,故A正确;
C.根据
可得
所以B的运动加速度大于A的运动加速度,故C正确;
D.由于B卫星轨道运行周期为2小时,是地球自转周期的,B卫星一天内12次看到日出日落,故D正确。
故选ACD。
12.BC
【详解】根据v-t图像的斜率表示加速度,可是两星球表面重力加速度之比为
A.根据
可得
得到,故A错误;
B.由
联立可得
得到,故B正确;
C.由
联立上面式子得到
得出星球P和星球Q的第一宇宙速度之比为,故C正确;
D.由
可得
得出,故D错误。
故选BC。
13. B 周期T ACD 物体质量m、重力F
【详解】[1][2][3][4]根据
=mg
=m2R
设用秒表测得绕行星表面运动一周的时间即周期为T,用天平测得物体的质量为m,用测力计测得该物体的重力为F;
[5][6]则
g=
解得
R=
M=
14. 1.40 7.9 1.4
【详解】(1)[1]根据量程为10kg,最小分度为0.1kg,注意估读到最小分度的下一位,为1.40kg
(2)[2]根据表格知最低点小车和凹形桥模拟器中质量的平均值
解得
[3]根据牛顿运动定律知
代入数据解得
15.(1) ;(2)
【详解】(1)设地面附近重力加速度为,由火箭点火前体重计示数为可知,物体质量为
由第一宇宙速度公式
可得地球表面附近的重力加速度
联立解得该物体的质量为
(2)当飞船离地面高度为H时,物体所受万有引力为
而
对物体应用牛顿第二定律得
联立可得火箭上升的加速度
16.()见解析;();()
【详解】(1)设月球的质量为M,对任一卫星均有
得
常量.
(2)两卫星第一次相距最远时有
(3)对嫦娥1号有
M=πR3ρ
17.(1),;(2);(3)见解析
【详解】(1)由质量数与核电荷数守恒可知,核反应方程式为
核反应中的质量亏损
释放出的核能
(2)银河系的年龄为,每秒钟银河系产生的能量约为,则产生的总能量为,根据核反应释放的能量,计算核反应产生的氦的质量
(3)宇宙诞生之初,氦的含量
由估算结果可知,远小于的实际值,所以银河系中的氦主要是宇宙诞生后不久生成的。
18.(1)2R;(2)
【详解】(1)设物体质量为m,星球质量为M,星球的自转周期为T,物体在星球两极时,万有引力等于重力,即
物体在星球赤道上随星球自转时,向心力由万有引力的一个分力提供,另一个分力就是重力,有
因为
得
该星球的同步卫星的周期等于自转周期T,则有
联立解得
(2)在星球赤道上,有
可得
又因星球的体积
所以该星球的密度
