2022—2023学年人教版数学八年级下册第19章一次函数专题复习课件(共22张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册第19章一次函数专题复习课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 237.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 17:16:03 | ||
图片预览





文档简介
(共22张PPT)
一、一次函数的定义:
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
=0
≠0
思 考
kx
y=k xn +b为一次函数的条件是什么
一. x次数n=1
二. 系数 k ≠0
2:函数y=(k+2)x+( -4)为正比例
函数,则k为何值
1.下列函数中,哪些是一次函数
k=2
答:
(1)是 (2)不是 (3)是 (4)不是
练一练:
3. 若函数 是正比例函数,则m= 。
5
求出下列函数中自变量的取值范围
(1)
(2)
(3)
二、自变量的取值范围
分式的分母不为0
被开方数(式)为非负数
与实际问题有关系的,应使实际问题有意义
n≥1
x≠-2
k≤1且k≠-1
练一练:
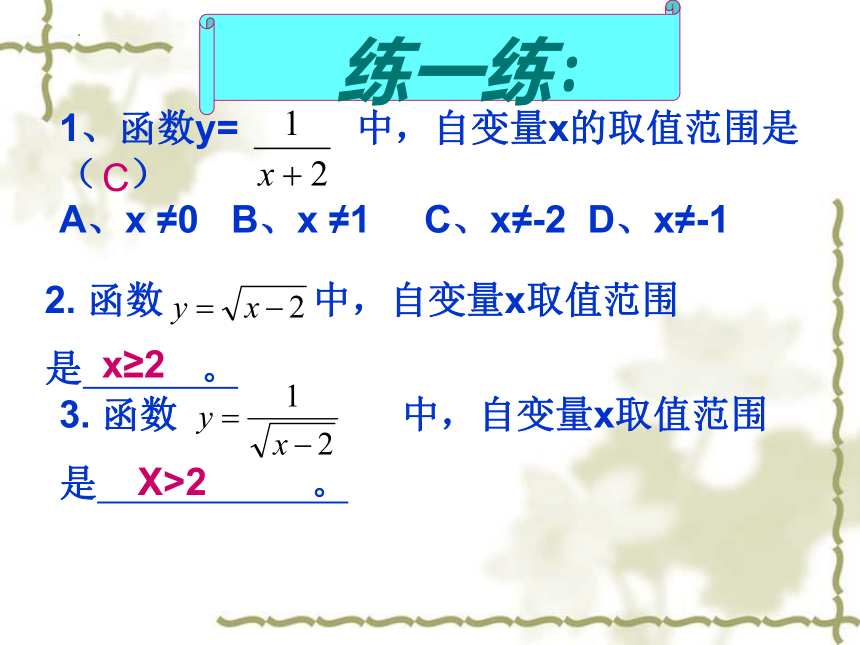
1、函数y= 中,自变量x的取值范围是( )
A、x ≠0 B、x ≠1 C、x≠-2 D、x≠-1
C
2. 函数 中,自变量x取值范围
是 。
3. 函数 中,自变量x取值范围
是 。
x≥2
X>2
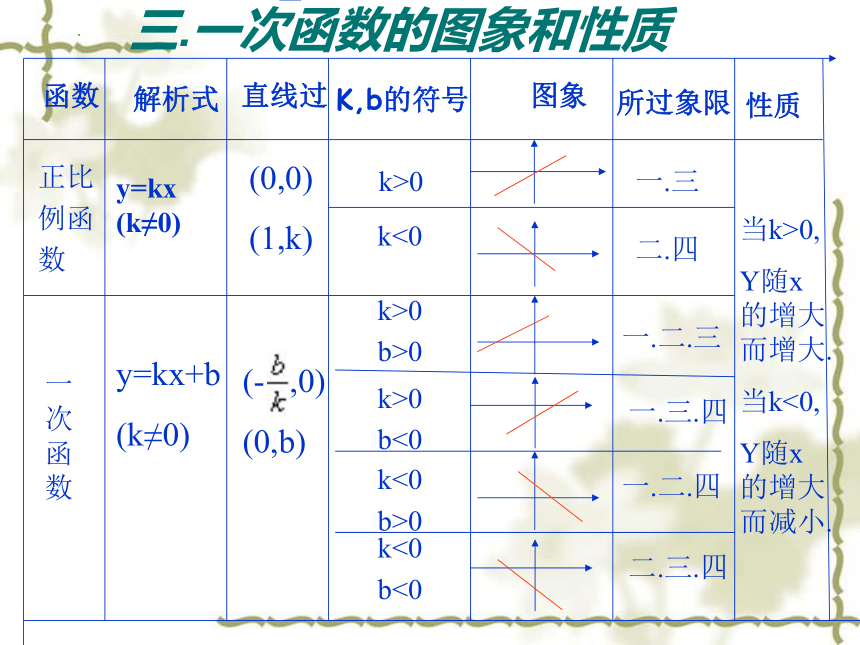
正比
例函
数
一次函数
y=kx+b
(k≠0)
(0,0)
(1,k)
(- ,0)
(0,b)
k>0
一.三
二.四
一.二.三
一.三.四
一.二.四
二.三.四
当k>0,
Y随x的增大而增大.
当k<0,
Y随x的增大而减小.
y=kx (k≠0)
k<0
k>0
b>0
k>0
b<0
k<0
b>0
k<0
b<0
三.一次函数的图象和性质
函数
解析式
直线过
K,b的符号
图象
所过象限
性质
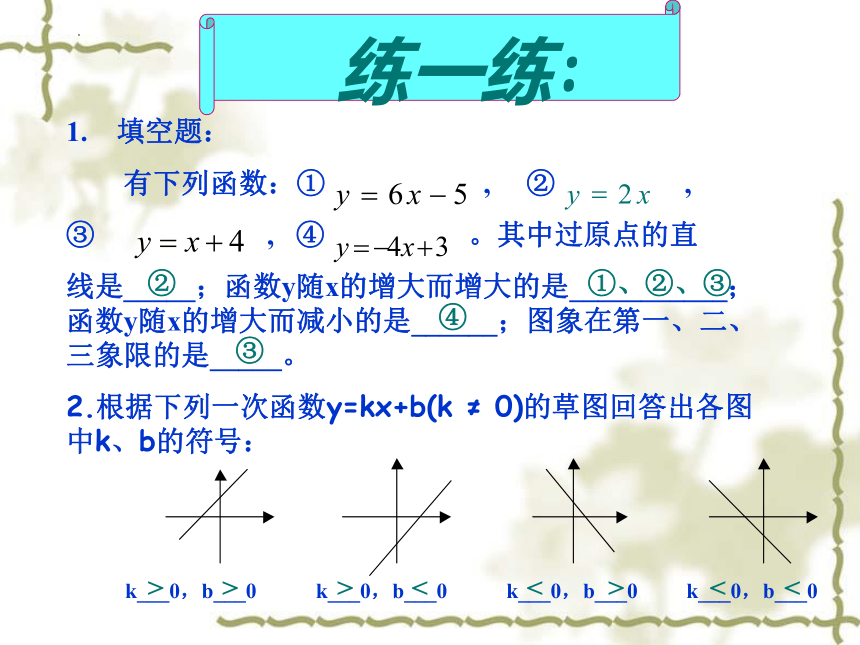
1. 填空题:
有下列函数:① , ② ,
③ , ④ 。其中过原点的直
线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____。
②
①、②、③
④
③
x
y
2
=
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
2.根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:
<
>
<
<
<
>
>
>
<
<
练一练:
3.函数y=(k+2)x+(2k-4)
(1)当k 时,函数图象过原点。
(2)当k 时, y随x的增大而减小。
4.函数y=kx+b 当k>0,b<0时,此函数图象不经过 的象限是
5.一次函数y=(a-5)x+(a-3)的图像不经过第三象限,则a的取值范围 _______
=2
﹤-2
第二象限
3≤a﹤5
6.已知一次函数 经过 象
限,当x逐渐增大时,函数值y逐渐 ;
一,三,四
增大
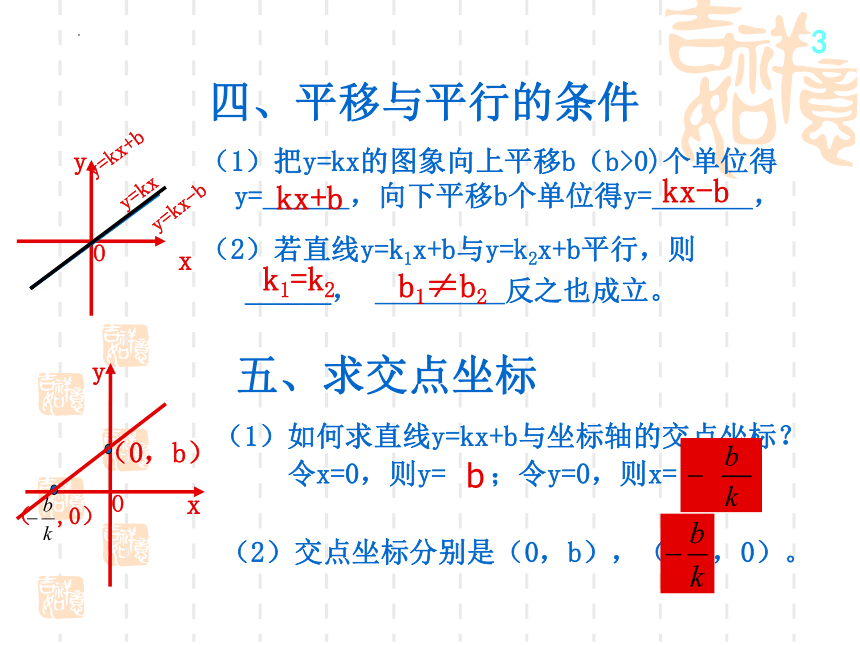
四、平移与平行的条件
(1)把y=kx的图象向上平移b(b>0)个单位得y= ,向下平移b个单位得y= ,
kx+b
(2)若直线y=k1x+b与y=k2x+b平行,则
______, 反之也成立。
(1)如何求直线y=kx+b与坐标轴的交点坐标?
令x=0,则y= ;令y=0,则x=
(2)交点坐标分别是(0,b),( ,0)。
b
五、求交点坐标
b1≠b2
k1=k2
kx-b
x
y
O
(0,b)
( ,0)
x
y
O
y=kx
y=kx+b
y=kx-b
3
1、一次函数y=2x+3的图像沿y轴向下平移2个单位,那么所得图像的函数解析式是( )
A、y=2x-3 B、y=2x+2 C 、y=2x+1 D、y=2x
练一练:
2、函数y=5x-4 向上平移5个单位,则得的函数解析式为 。
3、若直线y=kx+b平行直线y=-3x+2,且与y轴交点为(0,5),则k= ,b= 。
4. 已知直线y=kx+b平行与直线y=-2x,且与y轴交于点(0,-2),则k=___ ,b=___.
C
y=5x+1
-3
5
-2
-2
1. 直线y=-x+1与x轴的交点坐标为_______,与Y轴的交点坐标为_______。
(1,0)
(0,1)
2. 一次函数y= 与x轴的交点坐标 ,
与y轴的交点坐标是_______________
解析:与x轴交点,令y=0,-x+1=0,得x=1,(1,0)
与y轴交点, 令x=0, y=0+1=1, (0,1)
(10,0)
(0,-5)
3. 若一次函数y=3x-b的图象经过点P(1,-1),
则b= .
4
4. 函数y=3x-2,当x=0时,y= ,当y=0时,x= .
-2
2/3
六、求两条直线的交点坐标
求函数y=2x-1与函数y=-0.5x+1交点的坐标
为 。
解析: 求两条直线交点的坐标,只需将两条直线解析式构成一个方程组,解得方程组的解即为直线交点坐标。
解得
(0.8,0.6)
练习:直线y=3-x与直线y=3x-5的交点坐标是 。
(2,1)
七、一次函数与一元一次方程之间的关系
求一元一次方程ax+b=0(a,b是常数,a≠0)的解,从“数”上看就是x为何值时函数y= ax+b的值为0.
求一元一次方程ax+b=0(a, b是常数,a≠0)的解,从“形”上看就是求直线y= ax+b与 x 轴交点的横坐标.
练一练:
1. 如图, 一条直线y=kx+b经过点A,则方程kx+b=0的解是 。
x
y
0
-5
A
X=-5
第1题
x
y
0
-4
2
第2题
2. 已知一次函数y=kx+b的图象如图所示,则方程kx+b=0的解是 。
X=2
八、一次函数与一元一次不等式之间的关系
小结:一条直线找函数值的大小时,以直线与x轴的交点为分界线,直线在x轴上方的函数值y>0,在x轴下方的函数值y<0;交点右边的x>,左边的x<。
小结:两条直线找函数值的大小,以交点为分界线,上边的函数比下边的函数值大,交点右边的x>,左边的x<。
练一练:
1. 如图,一次函数解析式y=ax+b的图象经过A,B两点,则关于x的不等式ax+b<0的解集是 。
x
y
0
-1
A
2
B
第1题
x
y
0
-2
A
3
B
第2题
2. 如图,一次函数y=kx+b的图象经过点A,B,则关于x的不等式kx+b>0的解集是 。
X<2
X>-2
.
-1
3
0
x
y
X<-1
八、一次函数与二元一次方程组之间的关系
两个函数图象的交点即为方程组的解,反过来方程组的解即为两个函数图象的交点
。
y
x
1
0
1
-1
-2
0
x
y
.
X=-1
.
。
当x 时,函数y=-5x+1与y=3x+17的值相等, 函数值是 。
解析: 令-5x+1=3x+17 ,得x=-2
y= -5×2+1=-9
=-2
9
某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克2.5元。小王携带现金3000元到这市场采购苹果,并以批发价买进。如果购买的苹果为x千克,小王付款后还剩现金y元,试写出y关于x的函数解析式,并指出自变量x的取值范围。
解: 依题意,y=3000-2.5x
X的取值范围是100≤x≤1200
已知等腰三角形周长为20
(1)写出底边长y关于腰长x的函数解析式
(2)写出自变量的取值范围
(3)在直角坐标系中,画出函数图象
解: (1)y=20-2x
(2)因为y>0
所以x<10
又因为三角形两边之和大于第三边
所以2x>20-2x,得x>5
所以510
20
y
0
x
如图,已知直线 经过点A(-1,0)与点B(2,3),另一条直线 经过点B,且与x轴交于点P
(1)求直线 的解析式
(2)若⊿APB的面积为3,求m的值
y
x
-1
A
2
3
B
P(m,n)
一、一次函数的定义:
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
=0
≠0
思 考
kx
y=k xn +b为一次函数的条件是什么
一. x次数n=1
二. 系数 k ≠0
2:函数y=(k+2)x+( -4)为正比例
函数,则k为何值
1.下列函数中,哪些是一次函数
k=2
答:
(1)是 (2)不是 (3)是 (4)不是
练一练:
3. 若函数 是正比例函数,则m= 。
5
求出下列函数中自变量的取值范围
(1)
(2)
(3)
二、自变量的取值范围
分式的分母不为0
被开方数(式)为非负数
与实际问题有关系的,应使实际问题有意义
n≥1
x≠-2
k≤1且k≠-1
练一练:
1、函数y= 中,自变量x的取值范围是( )
A、x ≠0 B、x ≠1 C、x≠-2 D、x≠-1
C
2. 函数 中,自变量x取值范围
是 。
3. 函数 中,自变量x取值范围
是 。
x≥2
X>2
正比
例函
数
一次函数
y=kx+b
(k≠0)
(0,0)
(1,k)
(- ,0)
(0,b)
k>0
一.三
二.四
一.二.三
一.三.四
一.二.四
二.三.四
当k>0,
Y随x的增大而增大.
当k<0,
Y随x的增大而减小.
y=kx (k≠0)
k<0
k>0
b>0
k>0
b<0
k<0
b>0
k<0
b<0
三.一次函数的图象和性质
函数
解析式
直线过
K,b的符号
图象
所过象限
性质
1. 填空题:
有下列函数:① , ② ,
③ , ④ 。其中过原点的直
线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____。
②
①、②、③
④
③
x
y
2
=
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
2.根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:
<
>
<
<
<
>
>
>
<
<
练一练:
3.函数y=(k+2)x+(2k-4)
(1)当k 时,函数图象过原点。
(2)当k 时, y随x的增大而减小。
4.函数y=kx+b 当k>0,b<0时,此函数图象不经过 的象限是
5.一次函数y=(a-5)x+(a-3)的图像不经过第三象限,则a的取值范围 _______
=2
﹤-2
第二象限
3≤a﹤5
6.已知一次函数 经过 象
限,当x逐渐增大时,函数值y逐渐 ;
一,三,四
增大
四、平移与平行的条件
(1)把y=kx的图象向上平移b(b>0)个单位得y= ,向下平移b个单位得y= ,
kx+b
(2)若直线y=k1x+b与y=k2x+b平行,则
______, 反之也成立。
(1)如何求直线y=kx+b与坐标轴的交点坐标?
令x=0,则y= ;令y=0,则x=
(2)交点坐标分别是(0,b),( ,0)。
b
五、求交点坐标
b1≠b2
k1=k2
kx-b
x
y
O
(0,b)
( ,0)
x
y
O
y=kx
y=kx+b
y=kx-b
3
1、一次函数y=2x+3的图像沿y轴向下平移2个单位,那么所得图像的函数解析式是( )
A、y=2x-3 B、y=2x+2 C 、y=2x+1 D、y=2x
练一练:
2、函数y=5x-4 向上平移5个单位,则得的函数解析式为 。
3、若直线y=kx+b平行直线y=-3x+2,且与y轴交点为(0,5),则k= ,b= 。
4. 已知直线y=kx+b平行与直线y=-2x,且与y轴交于点(0,-2),则k=___ ,b=___.
C
y=5x+1
-3
5
-2
-2
1. 直线y=-x+1与x轴的交点坐标为_______,与Y轴的交点坐标为_______。
(1,0)
(0,1)
2. 一次函数y= 与x轴的交点坐标 ,
与y轴的交点坐标是_______________
解析:与x轴交点,令y=0,-x+1=0,得x=1,(1,0)
与y轴交点, 令x=0, y=0+1=1, (0,1)
(10,0)
(0,-5)
3. 若一次函数y=3x-b的图象经过点P(1,-1),
则b= .
4
4. 函数y=3x-2,当x=0时,y= ,当y=0时,x= .
-2
2/3
六、求两条直线的交点坐标
求函数y=2x-1与函数y=-0.5x+1交点的坐标
为 。
解析: 求两条直线交点的坐标,只需将两条直线解析式构成一个方程组,解得方程组的解即为直线交点坐标。
解得
(0.8,0.6)
练习:直线y=3-x与直线y=3x-5的交点坐标是 。
(2,1)
七、一次函数与一元一次方程之间的关系
求一元一次方程ax+b=0(a,b是常数,a≠0)的解,从“数”上看就是x为何值时函数y= ax+b的值为0.
求一元一次方程ax+b=0(a, b是常数,a≠0)的解,从“形”上看就是求直线y= ax+b与 x 轴交点的横坐标.
练一练:
1. 如图, 一条直线y=kx+b经过点A,则方程kx+b=0的解是 。
x
y
0
-5
A
X=-5
第1题
x
y
0
-4
2
第2题
2. 已知一次函数y=kx+b的图象如图所示,则方程kx+b=0的解是 。
X=2
八、一次函数与一元一次不等式之间的关系
小结:一条直线找函数值的大小时,以直线与x轴的交点为分界线,直线在x轴上方的函数值y>0,在x轴下方的函数值y<0;交点右边的x>,左边的x<。
小结:两条直线找函数值的大小,以交点为分界线,上边的函数比下边的函数值大,交点右边的x>,左边的x<。
练一练:
1. 如图,一次函数解析式y=ax+b的图象经过A,B两点,则关于x的不等式ax+b<0的解集是 。
x
y
0
-1
A
2
B
第1题
x
y
0
-2
A
3
B
第2题
2. 如图,一次函数y=kx+b的图象经过点A,B,则关于x的不等式kx+b>0的解集是 。
X<2
X>-2
.
-1
3
0
x
y
X<-1
八、一次函数与二元一次方程组之间的关系
两个函数图象的交点即为方程组的解,反过来方程组的解即为两个函数图象的交点
。
y
x
1
0
1
-1
-2
0
x
y
.
X=-1
.
。
当x 时,函数y=-5x+1与y=3x+17的值相等, 函数值是 。
解析: 令-5x+1=3x+17 ,得x=-2
y= -5×2+1=-9
=-2
9
某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克2.5元。小王携带现金3000元到这市场采购苹果,并以批发价买进。如果购买的苹果为x千克,小王付款后还剩现金y元,试写出y关于x的函数解析式,并指出自变量x的取值范围。
解: 依题意,y=3000-2.5x
X的取值范围是100≤x≤1200
已知等腰三角形周长为20
(1)写出底边长y关于腰长x的函数解析式
(2)写出自变量的取值范围
(3)在直角坐标系中,画出函数图象
解: (1)y=20-2x
(2)因为y>0
所以x<10
又因为三角形两边之和大于第三边
所以2x>20-2x,得x>5
所以5
20
y
0
x
如图,已知直线 经过点A(-1,0)与点B(2,3),另一条直线 经过点B,且与x轴交于点P
(1)求直线 的解析式
(2)若⊿APB的面积为3,求m的值
y
x
-1
A
2
3
B
P(m,n)
