2022-2023学年京改版九年级数学下册 25.1求概率的方法达标练习 (无答案)
文档属性
| 名称 | 2022-2023学年京改版九年级数学下册 25.1求概率的方法达标练习 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 223.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 17:23:49 | ||
图片预览


文档简介
京改版九年级数学下册25.1求概率的方法达标练习
一、单选题
1、一个不透明的盒子里装有a个除颜色外完全相同的球,其中有6个白球,每次将球充分搅匀后,任意摸出1个球记下颜色然后再放回盒子里,通过如此大量重复试验,发现摸到白球的频率稳定在0.4左右,则a的值约为( )
A.10 B.12 C.15 D.18
2、在一个不透明的袋子里装有若干个白球和15个黄球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过很多次重复试验,发现摸到黄球的频率稳定在0.75,则袋中白球有( )
A.5个 B.15个 C.20个 D.35个
3、不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A. B. C. D.
4、如图,点D在的边上,连接,点P的位置如图所示,在图中随机选择一个三角形,则点P在选择的三角形内部的概率是( )
A. B. C. D.1
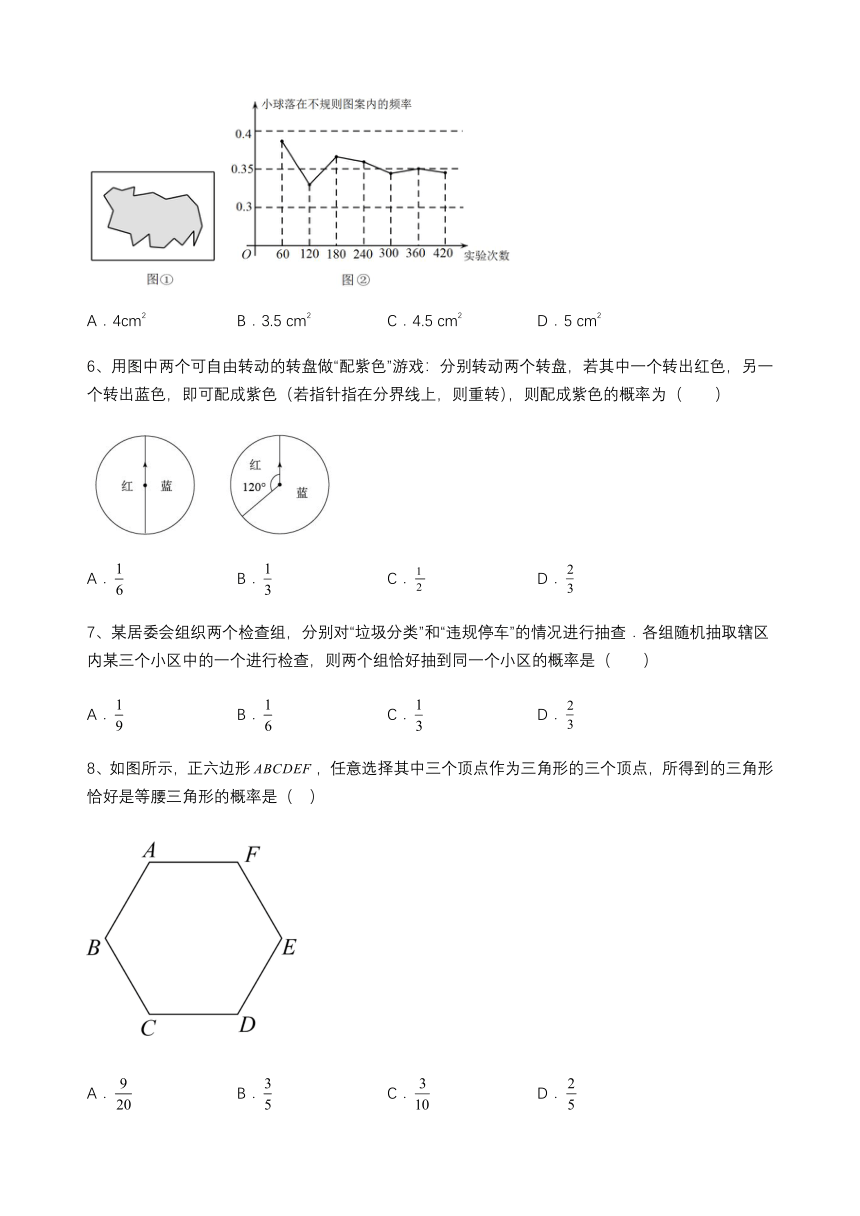
5、小明为估计一个不规则图案的面积,采取了以下办法:首先用一个面积为10cm2的长方形将不规则图案围起来(如图①);然后在一固定位置随机朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在边界线上或长方形区域外不计试验结果);最后将若干次有效试验的结果绘制成了图②所示的折线统计图.请估计不规则图案的面积大约为( )
A.4cm2 B.3.5 cm2 C.4.5 cm2 D.5 cm2
6、用图中两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色,即可配成紫色(若指针指在分界线上,则重转),则配成紫色的概率为( )
A. B. C. D.
7、某居委会组织两个检查组,分别对“垃圾分类”和“违规停车”的情况进行抽查.各组随机抽取辖区内某三个小区中的一个进行检查,则两个组恰好抽到同一个小区的概率是( )
A. B. C. D.
8、如图所示,正六边形,任意选择其中三个顶点作为三角形的三个顶点,所得到的三角形恰好是等腰三角形的概率是( )
A. B. C. D.
二、填空题
1、一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是___________.
2、甲、乙、丙三位同学打乒乓球,想通过“手心手背”游戏来决定其中哪两人先打.规则如下:三人同时各用一只手随机出示手心或手背,若只有两人手势相同(都是手心或都是手背),则这两人先打;若三人手势相同,则重新决定.那么通过一次“手心手背”游戏能决定甲打乒乓球的概率是_________.
3、有5张相同的卡片,卡片正面分别标有-2,,,,,将卡片背面朝上,从中随机抽取1张,则抽取的卡片上的数是正数的概率为______.
4、在课后服务时间,甲乙两班进行篮球比赛,在选择比赛场地时,裁判员采用了同时掷两枚完全相同硬币的方法:如果两枚硬币朝上的面不同,则甲班优先选择场地;否则乙班优先选择场地.这种选择场地的方法对两个班级___________(填“公平”或“不公平”).
5、一个不透明的袋子中装有个小球,其中个红球、个绿球,这些小球除颜色外无其他差别.从袋子中随机摸出一个小球,则摸出的小球是绿球的概率是_____________.
6、不透明袋子中装有1个红球和2个黄球,这些球除颜色外无其他差别.从袋子中随机摸出1个球,摸出红球的概率是 _________ .
三、解答题
1、寒冬战疫,西安常安,感谢每一位为这座城拼命的人!一个不透明的口袋里装有分别标有汉字“西”、“安”、“常”、“安”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一球,球上的汉字刚好是“安”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用画树状图或列表法,求出甲取出的两个球上的汉字恰能组成“西安”的概率。(汉字不分先后顺序)
2、一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数n 200 300 400 500 600 700 800 1000
摸到红球次数m 151 221 289 358 429 497 571 702
摸到红球频率 0.75 0.74 0.72 0.72 0.72 0.71 a b
(1)表格中a= ;b= ;(精确到0.01)
(2)估计从袋子中摸出一个球恰好是红球的概率约为 ;(精确到0.1)
(3)如果袋子中有14个红球,1个白球,若干黄球,估计袋子中黄球的个数和摸到黄球的概率?
3、小明和小亮是上海某高校的大学生,他们参加世博志愿者选拔并与甲、乙二人都进入了前4名.现从这4名入选者中确定2名作为志愿者.试用画树形图或列表的方法求出:
(1)小明和小亮同时入选的概率;
(2)小明和小亮至少有一人入选的概率.
4、2022年3月22日至28日是第三十五届“中国水周”,在此期间,某校举行了主题“为推进地下水超采综合治理,复苏河湖生态环境”的水资源保护知识竞赛.为了了解本次知识竞赛成绩的分布情况,从参赛学生中随机抽取了150名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
成绩x/分 频数 频率
15 0.1
a 0.2
45 b
60 c
(1)表中___________,___________,___________;
(2)请补全频数分布直方图:
(3)若某班恰有3名女生和1名男生的初赛成绩均为99分,从这4名学生中随机选取2名学生参加复赛,请用列表法或画树状图法求选出的2名学生恰好为一名男生、一名女生的概率.
5、一个小球在如图所示的方格地板上自由地滚动,并随机停留在某块地板上,每块地板大小、质地完全相同.
(1)该小球停留在黑色区域的概率是多少?
(2)甲,乙两人比赛,小球落到白色区域甲赢,落在黑色区域乙赢,你认为这个游戏公平吗?
一、单选题
1、一个不透明的盒子里装有a个除颜色外完全相同的球,其中有6个白球,每次将球充分搅匀后,任意摸出1个球记下颜色然后再放回盒子里,通过如此大量重复试验,发现摸到白球的频率稳定在0.4左右,则a的值约为( )
A.10 B.12 C.15 D.18
2、在一个不透明的袋子里装有若干个白球和15个黄球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过很多次重复试验,发现摸到黄球的频率稳定在0.75,则袋中白球有( )
A.5个 B.15个 C.20个 D.35个
3、不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A. B. C. D.
4、如图,点D在的边上,连接,点P的位置如图所示,在图中随机选择一个三角形,则点P在选择的三角形内部的概率是( )
A. B. C. D.1
5、小明为估计一个不规则图案的面积,采取了以下办法:首先用一个面积为10cm2的长方形将不规则图案围起来(如图①);然后在一固定位置随机朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在边界线上或长方形区域外不计试验结果);最后将若干次有效试验的结果绘制成了图②所示的折线统计图.请估计不规则图案的面积大约为( )
A.4cm2 B.3.5 cm2 C.4.5 cm2 D.5 cm2
6、用图中两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色,即可配成紫色(若指针指在分界线上,则重转),则配成紫色的概率为( )
A. B. C. D.
7、某居委会组织两个检查组,分别对“垃圾分类”和“违规停车”的情况进行抽查.各组随机抽取辖区内某三个小区中的一个进行检查,则两个组恰好抽到同一个小区的概率是( )
A. B. C. D.
8、如图所示,正六边形,任意选择其中三个顶点作为三角形的三个顶点,所得到的三角形恰好是等腰三角形的概率是( )
A. B. C. D.
二、填空题
1、一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是___________.
2、甲、乙、丙三位同学打乒乓球,想通过“手心手背”游戏来决定其中哪两人先打.规则如下:三人同时各用一只手随机出示手心或手背,若只有两人手势相同(都是手心或都是手背),则这两人先打;若三人手势相同,则重新决定.那么通过一次“手心手背”游戏能决定甲打乒乓球的概率是_________.
3、有5张相同的卡片,卡片正面分别标有-2,,,,,将卡片背面朝上,从中随机抽取1张,则抽取的卡片上的数是正数的概率为______.
4、在课后服务时间,甲乙两班进行篮球比赛,在选择比赛场地时,裁判员采用了同时掷两枚完全相同硬币的方法:如果两枚硬币朝上的面不同,则甲班优先选择场地;否则乙班优先选择场地.这种选择场地的方法对两个班级___________(填“公平”或“不公平”).
5、一个不透明的袋子中装有个小球,其中个红球、个绿球,这些小球除颜色外无其他差别.从袋子中随机摸出一个小球,则摸出的小球是绿球的概率是_____________.
6、不透明袋子中装有1个红球和2个黄球,这些球除颜色外无其他差别.从袋子中随机摸出1个球,摸出红球的概率是 _________ .
三、解答题
1、寒冬战疫,西安常安,感谢每一位为这座城拼命的人!一个不透明的口袋里装有分别标有汉字“西”、“安”、“常”、“安”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一球,球上的汉字刚好是“安”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用画树状图或列表法,求出甲取出的两个球上的汉字恰能组成“西安”的概率。(汉字不分先后顺序)
2、一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数n 200 300 400 500 600 700 800 1000
摸到红球次数m 151 221 289 358 429 497 571 702
摸到红球频率 0.75 0.74 0.72 0.72 0.72 0.71 a b
(1)表格中a= ;b= ;(精确到0.01)
(2)估计从袋子中摸出一个球恰好是红球的概率约为 ;(精确到0.1)
(3)如果袋子中有14个红球,1个白球,若干黄球,估计袋子中黄球的个数和摸到黄球的概率?
3、小明和小亮是上海某高校的大学生,他们参加世博志愿者选拔并与甲、乙二人都进入了前4名.现从这4名入选者中确定2名作为志愿者.试用画树形图或列表的方法求出:
(1)小明和小亮同时入选的概率;
(2)小明和小亮至少有一人入选的概率.
4、2022年3月22日至28日是第三十五届“中国水周”,在此期间,某校举行了主题“为推进地下水超采综合治理,复苏河湖生态环境”的水资源保护知识竞赛.为了了解本次知识竞赛成绩的分布情况,从参赛学生中随机抽取了150名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
成绩x/分 频数 频率
15 0.1
a 0.2
45 b
60 c
(1)表中___________,___________,___________;
(2)请补全频数分布直方图:
(3)若某班恰有3名女生和1名男生的初赛成绩均为99分,从这4名学生中随机选取2名学生参加复赛,请用列表法或画树状图法求选出的2名学生恰好为一名男生、一名女生的概率.
5、一个小球在如图所示的方格地板上自由地滚动,并随机停留在某块地板上,每块地板大小、质地完全相同.
(1)该小球停留在黑色区域的概率是多少?
(2)甲,乙两人比赛,小球落到白色区域甲赢,落在黑色区域乙赢,你认为这个游戏公平吗?
