9.4.4 菱形的判定同步练习 (含答案)
文档属性
| 名称 | 9.4.4 菱形的判定同步练习 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 318.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-19 11:13:33 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
9.4 矩形、菱形、正方形
9.4.4 菱形的判定
知识总结:
菱形的判定方法总结:(1)有一组邻边相等的______________叫做菱形;
(2)四边相等的_____________是菱形;
(3)对角线____________________的平行四边形是菱形.
基础练习
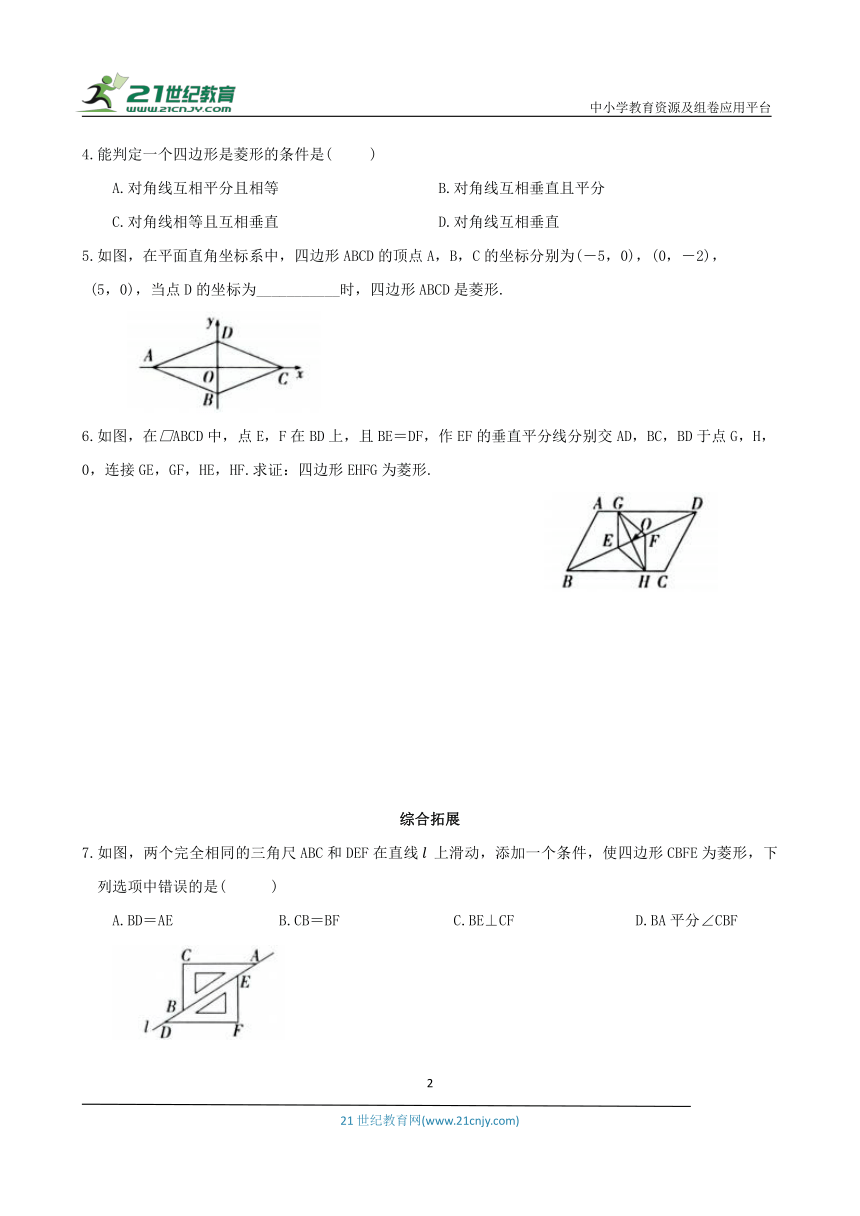
1.如图,在□ABCD中,对角线AC,BD交于点0,添加下列条件能使□ABCD是菱形的是( )
A.AC=BD B.∠BAD=90° C.AB=BC D.OB=OC
2.如图,在等腰△ABC中,AB=BC,将△ABC沿AC边翻折,点B落在D处,得到四边形ABCD,则能直接判定四边形ABCD是菱形的依据_____________________.
3.如图,在□ABCD中,点E,F分别为边AB,CD的中点,连接DE,BF,BD.当∠ADB=90°时,
求证:四边形DEBF是菱形.
4.能判定一个四边形是菱形的条件是( )
A.对角线互相平分且相等 B.对角线互相垂直且平分
C.对角线相等且互相垂直 D.对角线互相垂直
5.如图,在平面直角坐标系中,四边形ABCD的顶点A,B,C的坐标分别为(-5,0),(0,-2),
(5,0),当点D的坐标为___________时,四边形ABCD是菱形.
6.如图,在□ABCD中,点E,F在BD上,且BE=DF,作EF的垂直平分线分别交AD,BC,BD于点G,H,
0,连接GE,GF,HE,HF.求证:四边形EHFG为菱形.
综合拓展
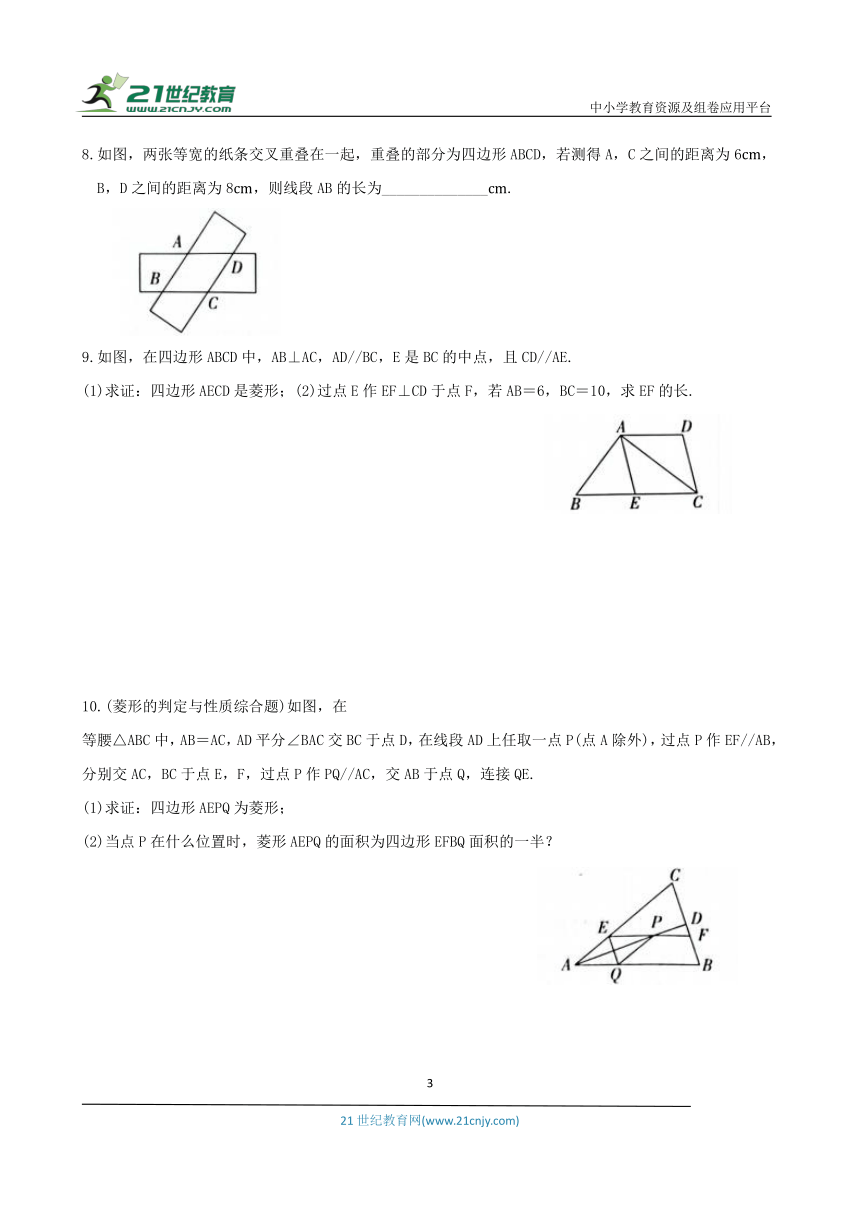
7.如图,两个完全相同的三角尺ABC和DEF在直线上滑动,添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
A.BD=AE B.CB=BF C.BE⊥CF D.BA平分∠CBF
8.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6,
B,D之间的距离为8,则线段AB的长为______________.
9.如图,在四边形ABCD中,AB⊥AC,AD//BC,E是BC的中点,且CD//AE.
(1)求证:四边形AECD是菱形;(2)过点E作EF⊥CD于点F,若AB=6,BC=10,求EF的长.
10.(菱形的判定与性质综合题)如图,在
等腰△ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF//AB,分别交AC,BC于点E,F,过点P作PQ//AC,交AB于点Q,连接QE.
(1)求证:四边形AEPQ为菱形;
(2)当点P在什么位置时,菱形AEPQ的面积为四边形EFBQ面积的一半?
11.(中考创新题型·阅读理解题)定义:一条对角线垂直平分另一条对角线的四边形叫做筝形,如图,筝形ABCD的对角线AC,BD相交于点0.且AC垂直平分BD.
(1)请结合图形,写出筝形两种不同类型的性质:
性质1:_____________________________;性质2:____________________________;
(2)若AB//CD,求证:四边形ABCD为菱形.
参考答案
1.C
2.四条边相等的四边形是菱形
3.证明:
∵四边形ABCD为平行四边形,∴AB=CD,AB//CD,
∵E,F分别为边AB,CD的中点,∴EB=AB,DF=CD.∴EB=DF,EB//DF,∴四边形DEBF为平行四边形,
∵∠ADB=90°,E为边AB的中点,∴DE=AB=EB,∴四边形DEBF是菱形.
4.B
5.(0,2)
6.证明:
∵四边形ABCD是平行四边形,∴AD//BC,∴∠ADB=∠CBD,
∵GH垂直平分EF,∴OE=OF,GH⊥EF,
∵BE=DF,∴BO=DO,∴△BOH≌△DOG(ASA),∴OH=OG,
又∵OE=OF,GH⊥EF,∴四边形EHFG为菱形.
7.A
8.5
【解析】如解图,过点A作AR⊥BC于点R,AS⊥CD于点S,连接AC,BD交于点0,由题意知,AD//BC,AB//CD,∴四边形ABCD是平行四边形.
∵两张纸条等宽 ∴AR=AS.
∵AR·BC=AS·CD,
∴BC=CD,∴四边形ABCD是菱形,∴AC⊥BD,OA=OC=AC=3cm,0B=0D=BD=4cm,
在R△A0B中,由勾股定理得AB===5cm.
9.(1)证明:∵AD//BC,AE//DC,∴四边形AECD是平行四边形,
∵AB⊥AC,∴∠BAC=90°,
∵E是BC的中点,∴AB=BC=CB.∴四边形AECD是菱形;
(2)解:如解图,过点A作AG⊥BC于点G,
∵AB=6,BC=10,∴AC==8,
∵=AB·AC=BC·AG,∴×6×8=×10AG,∴AG=
又∵=CD·EF=CE·AG,CD=CE,∴EF=AG=
10.(1)证明:∵EF//AB,PQ//AC,∴四边形AEPQ为平行四边形,∴∠BAD=∠EPA,
∵AD平分∠CAB,∴∠CAD=∠BAD,∴∠CAD=∠EPA,∴EA=EP,∴四边形AEPQ为菱形;
(2)解:当点P为EF的中点时,S菱形AEPQ=S四边形EFBQ,
∵四边形AEPQ为菱形,∴AP⊥EQ,
∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴EQ//BC,
又∵EF//AB,∴四边形EFBQ为平行四边形.
如解,过点E作EN⊥AB于点N,
∵S菱形AEPQ=EP·EN=S四边形EFBQ=EF·EN,
∴EP=EF,即当点P在EF的中点时,菱形AEPQ的面积为四边形EFBQ面积的一半.
11.(1)解:对角线互相垂直;是轴对称图形;(答案不唯一)
(2)证明:∵AC垂直平分BD,∴AB=AD,BO=DO,同理BC=DC,
∵AB//CD,∴∠ABO=∠ODC,∴△AOB≌△COD(ASA),
∴AB=CD,∴AB=CD=BC=AD,∴四边形ABCD为菱形.
21世纪教育网(www.21cnjy.com)
9.4 矩形、菱形、正方形
9.4.4 菱形的判定
知识总结:
菱形的判定方法总结:(1)有一组邻边相等的______________叫做菱形;
(2)四边相等的_____________是菱形;
(3)对角线____________________的平行四边形是菱形.
基础练习
1.如图,在□ABCD中,对角线AC,BD交于点0,添加下列条件能使□ABCD是菱形的是( )
A.AC=BD B.∠BAD=90° C.AB=BC D.OB=OC
2.如图,在等腰△ABC中,AB=BC,将△ABC沿AC边翻折,点B落在D处,得到四边形ABCD,则能直接判定四边形ABCD是菱形的依据_____________________.
3.如图,在□ABCD中,点E,F分别为边AB,CD的中点,连接DE,BF,BD.当∠ADB=90°时,
求证:四边形DEBF是菱形.
4.能判定一个四边形是菱形的条件是( )
A.对角线互相平分且相等 B.对角线互相垂直且平分
C.对角线相等且互相垂直 D.对角线互相垂直
5.如图,在平面直角坐标系中,四边形ABCD的顶点A,B,C的坐标分别为(-5,0),(0,-2),
(5,0),当点D的坐标为___________时,四边形ABCD是菱形.
6.如图,在□ABCD中,点E,F在BD上,且BE=DF,作EF的垂直平分线分别交AD,BC,BD于点G,H,
0,连接GE,GF,HE,HF.求证:四边形EHFG为菱形.
综合拓展
7.如图,两个完全相同的三角尺ABC和DEF在直线上滑动,添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
A.BD=AE B.CB=BF C.BE⊥CF D.BA平分∠CBF
8.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6,
B,D之间的距离为8,则线段AB的长为______________.
9.如图,在四边形ABCD中,AB⊥AC,AD//BC,E是BC的中点,且CD//AE.
(1)求证:四边形AECD是菱形;(2)过点E作EF⊥CD于点F,若AB=6,BC=10,求EF的长.
10.(菱形的判定与性质综合题)如图,在
等腰△ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF//AB,分别交AC,BC于点E,F,过点P作PQ//AC,交AB于点Q,连接QE.
(1)求证:四边形AEPQ为菱形;
(2)当点P在什么位置时,菱形AEPQ的面积为四边形EFBQ面积的一半?
11.(中考创新题型·阅读理解题)定义:一条对角线垂直平分另一条对角线的四边形叫做筝形,如图,筝形ABCD的对角线AC,BD相交于点0.且AC垂直平分BD.
(1)请结合图形,写出筝形两种不同类型的性质:
性质1:_____________________________;性质2:____________________________;
(2)若AB//CD,求证:四边形ABCD为菱形.
参考答案
1.C
2.四条边相等的四边形是菱形
3.证明:
∵四边形ABCD为平行四边形,∴AB=CD,AB//CD,
∵E,F分别为边AB,CD的中点,∴EB=AB,DF=CD.∴EB=DF,EB//DF,∴四边形DEBF为平行四边形,
∵∠ADB=90°,E为边AB的中点,∴DE=AB=EB,∴四边形DEBF是菱形.
4.B
5.(0,2)
6.证明:
∵四边形ABCD是平行四边形,∴AD//BC,∴∠ADB=∠CBD,
∵GH垂直平分EF,∴OE=OF,GH⊥EF,
∵BE=DF,∴BO=DO,∴△BOH≌△DOG(ASA),∴OH=OG,
又∵OE=OF,GH⊥EF,∴四边形EHFG为菱形.
7.A
8.5
【解析】如解图,过点A作AR⊥BC于点R,AS⊥CD于点S,连接AC,BD交于点0,由题意知,AD//BC,AB//CD,∴四边形ABCD是平行四边形.
∵两张纸条等宽 ∴AR=AS.
∵AR·BC=AS·CD,
∴BC=CD,∴四边形ABCD是菱形,∴AC⊥BD,OA=OC=AC=3cm,0B=0D=BD=4cm,
在R△A0B中,由勾股定理得AB===5cm.
9.(1)证明:∵AD//BC,AE//DC,∴四边形AECD是平行四边形,
∵AB⊥AC,∴∠BAC=90°,
∵E是BC的中点,∴AB=BC=CB.∴四边形AECD是菱形;
(2)解:如解图,过点A作AG⊥BC于点G,
∵AB=6,BC=10,∴AC==8,
∵=AB·AC=BC·AG,∴×6×8=×10AG,∴AG=
又∵=CD·EF=CE·AG,CD=CE,∴EF=AG=
10.(1)证明:∵EF//AB,PQ//AC,∴四边形AEPQ为平行四边形,∴∠BAD=∠EPA,
∵AD平分∠CAB,∴∠CAD=∠BAD,∴∠CAD=∠EPA,∴EA=EP,∴四边形AEPQ为菱形;
(2)解:当点P为EF的中点时,S菱形AEPQ=S四边形EFBQ,
∵四边形AEPQ为菱形,∴AP⊥EQ,
∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴EQ//BC,
又∵EF//AB,∴四边形EFBQ为平行四边形.
如解,过点E作EN⊥AB于点N,
∵S菱形AEPQ=EP·EN=S四边形EFBQ=EF·EN,
∴EP=EF,即当点P在EF的中点时,菱形AEPQ的面积为四边形EFBQ面积的一半.
11.(1)解:对角线互相垂直;是轴对称图形;(答案不唯一)
(2)证明:∵AC垂直平分BD,∴AB=AD,BO=DO,同理BC=DC,
∵AB//CD,∴∠ABO=∠ODC,∴△AOB≌△COD(ASA),
∴AB=CD,∴AB=CD=BC=AD,∴四边形ABCD为菱形.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
