2022-2023学年北师大版七年级数学下册2.1 两条直线的位置关系 基础练习 (无答案)
文档属性
| 名称 | 2022-2023学年北师大版七年级数学下册2.1 两条直线的位置关系 基础练习 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 200.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 00:00:00 | ||
图片预览

文档简介
2.1 两条直线的位置关系(基础练习)-北师大版七年级下册
一.选择题
.下列说法正确的是( )
A.若AC=BC,则点C为线段AB的中点
B.若,则射线OC为∠AOB平分线
C.若∠1+∠2+∠3=180°,则这三个角互补
D.若∠α与∠β互余,则∠α的补角比∠β大90°
.如图,在河边的A处,有一个牧童在放牛,牧童把牛牵到河边沿AB的路径走才能走最少的路,其依据是( )
A.过一点有且只有一条直线与已知直线垂直
B.垂线段最短
C.两点之间,线段最短
D.两点确定一条直线
.将一副直角三角板的顶点重合(如图所示),则∠1与∠2的大小关系是( )
A.∠1>∠2 B.∠1=∠2 C.∠1<∠2 D.不能确定
.已知∠A与∠B互余,∠A=56°15′,则∠B=( )
A.34°45′ B.33°45′ C.124°45′ D.123°45′
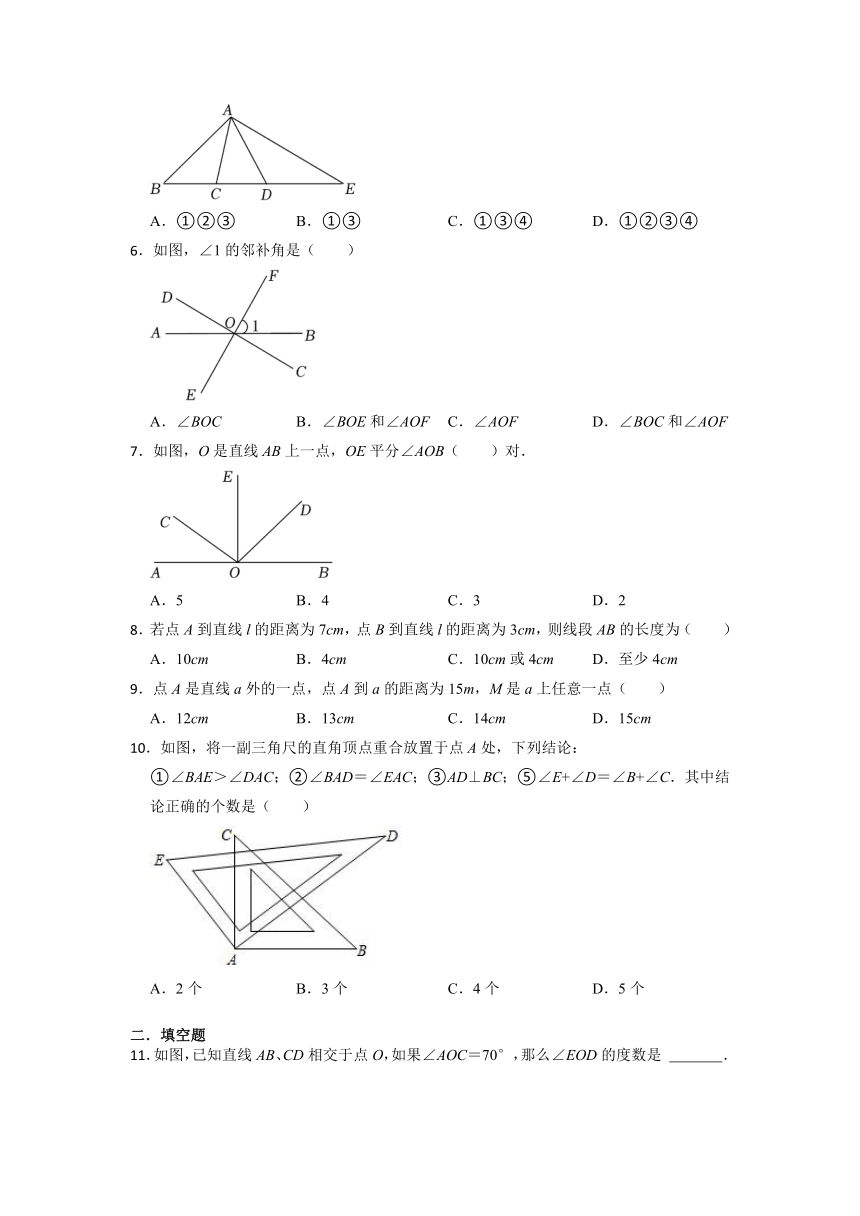
.如图,C,D在线段BE上,下列四个说法:
①直线CD上以B,C,D,E为端点的线段共有6条;
②图中有4对互为补角的角;
③若∠BAE=110°,∠DAC=40°,则以A为顶点的所有小于平角的角的度数和为370°;
④若BC=4,CD=3,DE=5(包含端点),则点F到点B,C,D,E的距离之和的最小值为15.
其中正确的说法是( )
A.①②③ B.①③ C.①③④ D.①②③④
.如图,∠1的邻补角是( )
A.∠BOC B.∠BOE和∠AOF C.∠AOF D.∠BOC和∠AOF
.如图,O是直线AB上一点,OE平分∠AOB( )对.
A.5 B.4 C.3 D.2
.若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为( )
A.10cm B.4cm C.10cm或4cm D.至少4cm
.点A是直线a外的一点,点A到a的距离为15m,M是a上任意一点( )
A.12cm B.13cm C.14cm D.15cm
.如图,将一副三角尺的直角顶点重合放置于点A处,下列结论:
①∠BAE>∠DAC;②∠BAD=∠EAC;③AD⊥BC;⑤∠E+∠D=∠B+∠C.其中结论正确的个数是( )
A.2个 B.3个 C.4个 D.5个
二.填空题
.如图,已知直线AB、CD相交于点O,如果∠AOC=70°,那么∠EOD的度数是 .
.一个角的补角比它的余角的三倍少10度,这个角是 度.
.如图,在∠AOB内部作OC⊥OB,OD平分∠AOB,则∠COD= .
.∠α与∠β互补,若∠α=47°37′,则∠β= .
.如图,直线AB,CD相交于点O,则∠COB= 度,∠BOD= 度.
三.解答题
.如图1所示,两个村庄A,B在河流1的两侧,同时向A、B两村供水,要使所铺设的管道最短
把河流1近似看作直线1,如图2所示.小明提出了这样的方案:过点A作直线l的垂线段AP,则点P为水泵站的位置.你同意小明的方案吗?若同意,那么你认为水泵站P应该建在什么位置?请在图3中作出来,并说明依据.
.如图,直线AB和CD相交于点O,∠COE=90°,∠BOE=58°.
(1)求∠AOC的度数;
(2)求∠EOF的度数.
.如图,已知OB平分∠AOC,且∠AOC的余角比∠BOC小30°.
(1)求∠AOB的度数;
(2)过点O作射线OD,使得∠AOD=∠AOC
.如图.已知∠MON=145°,∠AOC与∠BOC互余,OC平分∠MOB.
(1)在图①中.若∠AOC=40°,则∠BOC= °.∠NOB= °;
(2)在图①中,设∠AOC=α,∠NOB=β(必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在图①中,当∠AOB绕着点O顺时针转动到如图②的位置时,(2)中α与β之间的数量关系是否还成立?若成立;若不成立,请直接写出此时α与β之间的数量关系.
.(1)如图1,已知∠AOB=∠COD=90°,OE是∠AOC的角平分线,求∠AOE的度数;
(2)如图2,已知∠AOB=80°,∠COD=110°,求∠BOD的度数;
(3)如图3,当∠AOB=α,∠COD=β(n>1)时,请直接用含有α、β、n的式子表示∠BOD的值.
一.选择题
.下列说法正确的是( )
A.若AC=BC,则点C为线段AB的中点
B.若,则射线OC为∠AOB平分线
C.若∠1+∠2+∠3=180°,则这三个角互补
D.若∠α与∠β互余,则∠α的补角比∠β大90°
.如图,在河边的A处,有一个牧童在放牛,牧童把牛牵到河边沿AB的路径走才能走最少的路,其依据是( )
A.过一点有且只有一条直线与已知直线垂直
B.垂线段最短
C.两点之间,线段最短
D.两点确定一条直线
.将一副直角三角板的顶点重合(如图所示),则∠1与∠2的大小关系是( )
A.∠1>∠2 B.∠1=∠2 C.∠1<∠2 D.不能确定
.已知∠A与∠B互余,∠A=56°15′,则∠B=( )
A.34°45′ B.33°45′ C.124°45′ D.123°45′
.如图,C,D在线段BE上,下列四个说法:
①直线CD上以B,C,D,E为端点的线段共有6条;
②图中有4对互为补角的角;
③若∠BAE=110°,∠DAC=40°,则以A为顶点的所有小于平角的角的度数和为370°;
④若BC=4,CD=3,DE=5(包含端点),则点F到点B,C,D,E的距离之和的最小值为15.
其中正确的说法是( )
A.①②③ B.①③ C.①③④ D.①②③④
.如图,∠1的邻补角是( )
A.∠BOC B.∠BOE和∠AOF C.∠AOF D.∠BOC和∠AOF
.如图,O是直线AB上一点,OE平分∠AOB( )对.
A.5 B.4 C.3 D.2
.若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为( )
A.10cm B.4cm C.10cm或4cm D.至少4cm
.点A是直线a外的一点,点A到a的距离为15m,M是a上任意一点( )
A.12cm B.13cm C.14cm D.15cm
.如图,将一副三角尺的直角顶点重合放置于点A处,下列结论:
①∠BAE>∠DAC;②∠BAD=∠EAC;③AD⊥BC;⑤∠E+∠D=∠B+∠C.其中结论正确的个数是( )
A.2个 B.3个 C.4个 D.5个
二.填空题
.如图,已知直线AB、CD相交于点O,如果∠AOC=70°,那么∠EOD的度数是 .
.一个角的补角比它的余角的三倍少10度,这个角是 度.
.如图,在∠AOB内部作OC⊥OB,OD平分∠AOB,则∠COD= .
.∠α与∠β互补,若∠α=47°37′,则∠β= .
.如图,直线AB,CD相交于点O,则∠COB= 度,∠BOD= 度.
三.解答题
.如图1所示,两个村庄A,B在河流1的两侧,同时向A、B两村供水,要使所铺设的管道最短
把河流1近似看作直线1,如图2所示.小明提出了这样的方案:过点A作直线l的垂线段AP,则点P为水泵站的位置.你同意小明的方案吗?若同意,那么你认为水泵站P应该建在什么位置?请在图3中作出来,并说明依据.
.如图,直线AB和CD相交于点O,∠COE=90°,∠BOE=58°.
(1)求∠AOC的度数;
(2)求∠EOF的度数.
.如图,已知OB平分∠AOC,且∠AOC的余角比∠BOC小30°.
(1)求∠AOB的度数;
(2)过点O作射线OD,使得∠AOD=∠AOC
.如图.已知∠MON=145°,∠AOC与∠BOC互余,OC平分∠MOB.
(1)在图①中.若∠AOC=40°,则∠BOC= °.∠NOB= °;
(2)在图①中,设∠AOC=α,∠NOB=β(必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在图①中,当∠AOB绕着点O顺时针转动到如图②的位置时,(2)中α与β之间的数量关系是否还成立?若成立;若不成立,请直接写出此时α与β之间的数量关系.
.(1)如图1,已知∠AOB=∠COD=90°,OE是∠AOC的角平分线,求∠AOE的度数;
(2)如图2,已知∠AOB=80°,∠COD=110°,求∠BOD的度数;
(3)如图3,当∠AOB=α,∠COD=β(n>1)时,请直接用含有α、β、n的式子表示∠BOD的值.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
