2022-2023学年人教版七年级数学下册第一学段(5.1-6.3)综合练习题(含答案)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册第一学段(5.1-6.3)综合练习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 259.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 19:32:15 | ||
图片预览




文档简介
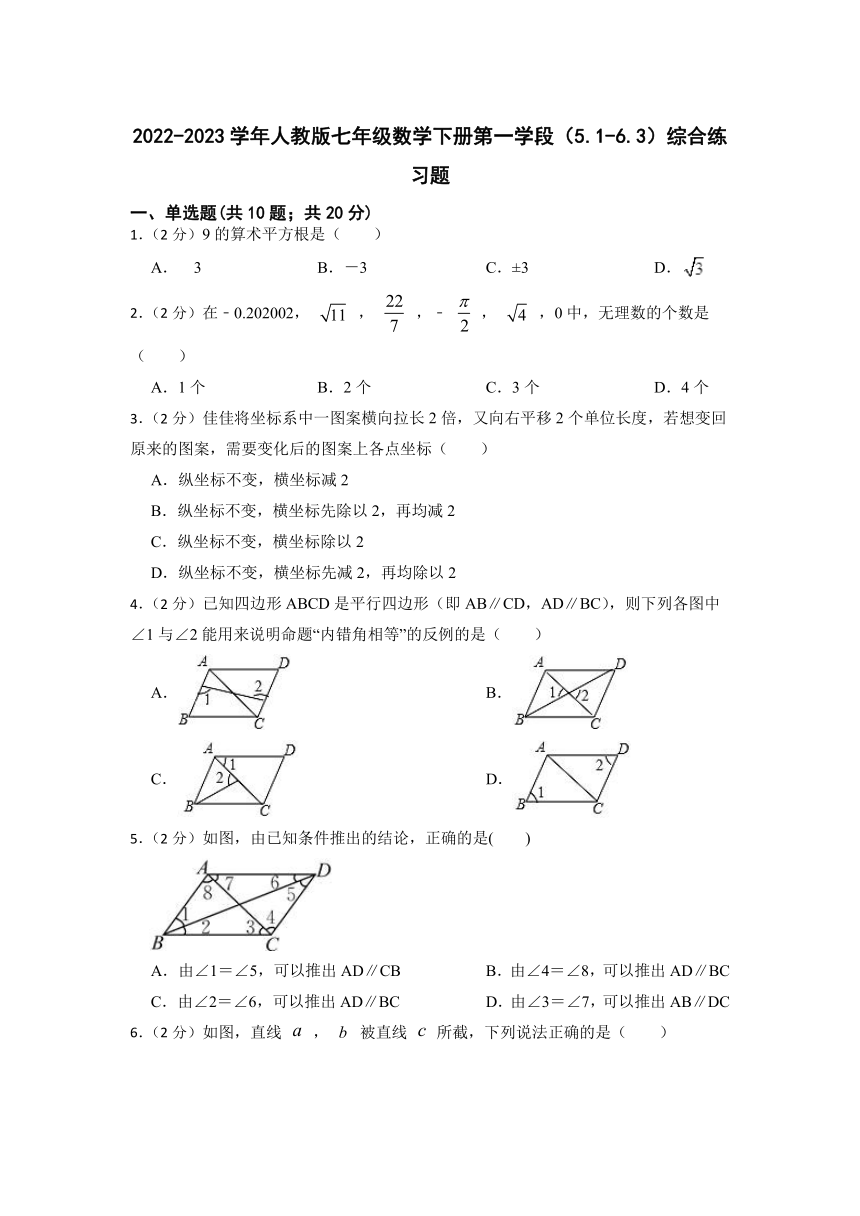
2022-2023学年人教版七年级数学下册第一学段(5.1-6.3)综合练习题
一、单选题(共10题;共20分)
1.(2分)9的算术平方根是( )
A. 3 B.-3 C.±3 D.
2.(2分)在﹣0.202002, , ,﹣ , ,0中,无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
3.(2分)佳佳将坐标系中一图案横向拉长2倍,又向右平移2个单位长度,若想变回原来的图案,需要变化后的图案上各点坐标( )
A.纵坐标不变,横坐标减2
B.纵坐标不变,横坐标先除以2,再均减2
C.纵坐标不变,横坐标除以2
D.纵坐标不变,横坐标先减2,再均除以2
4.(2分)已知四边形ABCD是平行四边形(即AB∥CD,AD∥BC),则下列各图中∠1与∠2能用来说明命题“内错角相等”的反例的是( )
A. B.
C. D.
5.(2分)如图,由已知条件推出的结论,正确的是( )
A.由∠1=∠5,可以推出AD∥CB B.由∠4=∠8,可以推出AD∥BC
C.由∠2=∠6,可以推出AD∥BC D.由∠3=∠7,可以推出AB∥DC
6.(2分)如图,直线 , 被直线 所截,下列说法正确的是( )
A.当 时,一定有
B.当 时,一定有
C.当 时,一定有
D.当 时,一定有
7.(2分)如图,直线a∥b,∠1=50°,∠2=40°,则∠3的度数为( )
A.40° B.90° C.50° D.100°
8.(2分)如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④
C.①③④ D.①②③④ 图4
9.(2分)如图,AB CD,∠ABE= ∠EBF,∠DCE= ∠ECF,设∠ABE=α,∠E=β,∠F=γ,则α,β,γ的数量关系是( )
A.4β﹣α+γ=360° B.3β﹣α+γ=360°
C.4β﹣α﹣γ=360° D.3β﹣2α﹣γ=360°
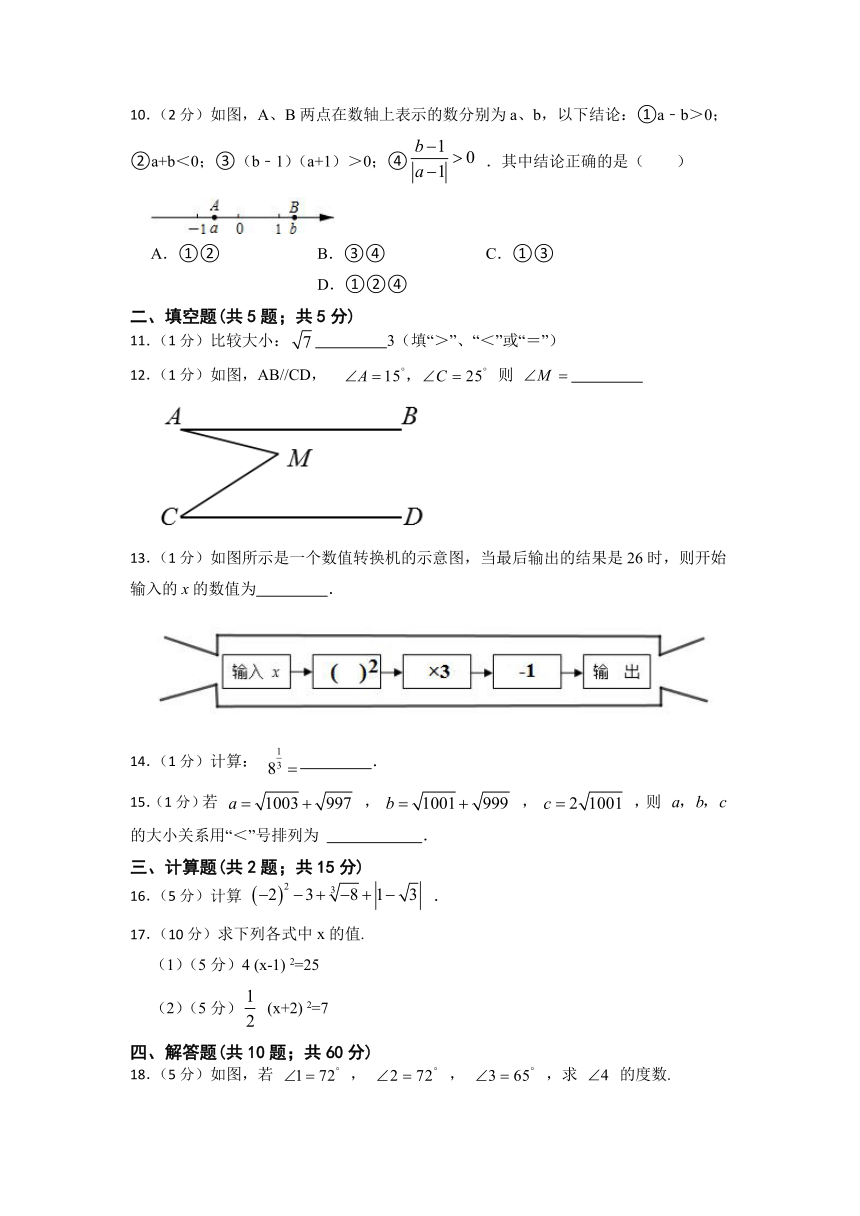
10.(2分)如图,A、B两点在数轴上表示的数分别为a、b,以下结论:①a﹣b>0;②a+b<0;③(b﹣1)(a+1)>0;④ .其中结论正确的是( )
A.①② B.③④ C.①③ D.①②④
二、填空题(共5题;共5分)
11.(1分)比较大小: 3(填“>”、“<”或“=”)
12.(1分)如图,AB//CD, 则
13.(1分)如图所示是一个数值转换机的示意图,当最后输出的结果是26时,则开始输入的x的数值为 .
14.(1分)计算: .
15.(1分)若 , , ,则 的大小关系用“<”号排列为 .
三、计算题(共2题;共15分)
16.(5分)计算 .
17.(10分)求下列各式中x的值.
(1)(5分)4 (x-1) 2=25
(2)(5分) (x+2) 2=7
四、解答题(共10题;共60分)
18.(5分)如图,若 , , ,求 的度数.
19.(5分)若一正数a的两个平方根分别是2m-3和5-m,求a的值.
20.(10分)(1)(5分)计算:
①
②
(2)(5分)求方程中的的值
①
②
21.(7分)已知:如图,DE⊥AC,垂足为点E,∠AGF=∠ABC,∠BFG+∠BDE=180°,
求证:BF⊥AC.
请完成下面的证明的过程,并在括号内注明理由.
证明:∵∠AGF=∠ABC(已知)
∴FG∥ ( )
∴∠BFG=∠FBC( )
∵∠BFG+∠BDE=180°(已知)
∴∠FBC+∠BDE=180°( )
∴BF∥DE( )
∴∠BFA= (两直线平行,同位角相等)
∵DE⊥AC(已知)
∴∠DEA=90°( )
∴∠BFA=90°(等量代换)
∴BF⊥AC(垂直的定义)
22.(5分)如图,∠A=50°,∠DBC=40°,AD∥BC,BD⊥DC.判断AB与CD的位置关系,并说明理由.
23.(5分)如图,DE⊥BC,AF⊥BC,∠1+∠2=180°.求证:∠FGA+∠CAB=180°
24.(9分)如图,AB与EF交于点B,CD与EF交于点D,根据图形,请补全下面这道题的解答过程.
(1)(1分)∵∠1=∠2(已知)
∴ CD( )
∴∠ABD+∠CDB = ( )
(2)(1分)∵∠BAC =65°,∠ACD=115°,( 已知 )
∴∠BAC+∠ACD=180° (等式性质)
∴AB CD ( )
(3)(1分)∵CD⊥AB于D,EF⊥AB于F,∠BAC=55°(已知)
∴∠ABD=∠CDF=90°( 垂直的定义)
∴ (同位角相等,两直线平行)
又∵∠BAC=55°,(已知)
∴∠ACD = ( )
25.(4分)阅读下面求 近似值的方法,回答问题:
①任取正数 ;
②令 则 ;
③ ,则 ;
……以此类推 次,得到
其中 称为 的 阶过剩近似值, 称为 的 阶不足近似值.仿照上述方法,求6的近似值.
①取正数 .
②于是 a2= ;则
③ 的3阶过剩近似值 是 ,3阶不足近似值是
26.(5分)如图 ,AB∥CD,且∠PMQ=2∠QMB,∠PNQ=2∠QND,判断∠P 与∠Q的数量关系,并说明理由.
27.(5分)如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM和∠NOC的度数.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】A
10.【答案】B
11.【答案】<
12.【答案】40°
13.【答案】3或-3
14.【答案】2
15.【答案】a<b<c
16.【答案】解:
17.【答案】(1)解:4(x﹣1)2=25
x﹣1
x 或x
(2)解:整理得:(x+2) 2=14
开方,得:x+2= 或x+2= ,∴x= 或x=
18.【答案】解:如图所示.∵ ,∴∠1=∠2,∴a∥b,∴∠3+∠4=180°.
∵∠3=65°,∴∠4=115°.
19.【答案】一正数a的两个平方根分别是2m-3和5-m,
(2m-3)+(5-m)=0,
m=-2,
2m-3=-7
(-7)2=49
20.【答案】(1)解:①原式=4-4×(-2)
=4+8
=12
②原式=-6-(-3)-(-1)+-(-1)
=
(2)解:①
解得或
②
解得
21.【答案】BC;同位角相等,两直线平行;两直线平行,内错角相等;等量代换;同旁内角互补,两直线平行;∠DEA;垂直的定义.
22.【答案】解:AB∥CD.理由:
∵AD∥BC,
∴∠ADB=∠DBC=40°.
∵BD⊥DC.
∴∠BDC=90°.
∴∠ADC=∠ADB+∠BDC=130°.
∴∠A+∠ADC=180°.
∴AB∥CD.
23.【答案】解:∵DE⊥BC,AF⊥BC,
∴AF∥DE,
∴∠2+∠3=180°.
∵∠1+∠2=180°,
∴∠1=∠3,
∴GF∥AC,
∴∠FGA+∠CAB=180°.
24.【答案】(1)AB;内错角相等,两直线平行;180°;两直线平行,同旁内角互补
(2)同旁内角互补,两直线平行
(3)AB;CD;125°;两直线平行,同旁内角互补
25.【答案】;;;
26.【答案】解:作QR∥AB,PL∥AB,∴RQ∥CD∥AB,PL∥AB∥CD
∴∠RQM=∠BMQ,∠RQN=∠QND,∠MPL=∠BMP,∠NPL=∠PND,
∵∠PMQ=2∠QMB,∠PNQ=2∠QND ,
∴∠PMB=3∠QMB ,∠PND=3∠QND ,
∵∠MQN=∠∠RQM+∠RQN=∠BMQ+∠QND,
∠MPN=∠MPL+∠NPL=∠BMP+∠PND,
∴∠MPN=3∠MQN,即∠P=3∠Q.
27.【答案】解:∵OE平分∠BON,
∴∠BON=2∠EON=2×20°=40°,
∴∠NOC=180°﹣∠BON=180°﹣40°=140°,
∠MOC=∠BON=40°,
∵AO⊥BC,
∴∠AOC=90°,
∴∠AOM=∠AOC﹣∠MOC=90°﹣40°=50°,
所以∠NOC=140°,∠AOM=50°.
一、单选题(共10题;共20分)
1.(2分)9的算术平方根是( )
A. 3 B.-3 C.±3 D.
2.(2分)在﹣0.202002, , ,﹣ , ,0中,无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
3.(2分)佳佳将坐标系中一图案横向拉长2倍,又向右平移2个单位长度,若想变回原来的图案,需要变化后的图案上各点坐标( )
A.纵坐标不变,横坐标减2
B.纵坐标不变,横坐标先除以2,再均减2
C.纵坐标不变,横坐标除以2
D.纵坐标不变,横坐标先减2,再均除以2
4.(2分)已知四边形ABCD是平行四边形(即AB∥CD,AD∥BC),则下列各图中∠1与∠2能用来说明命题“内错角相等”的反例的是( )
A. B.
C. D.
5.(2分)如图,由已知条件推出的结论,正确的是( )
A.由∠1=∠5,可以推出AD∥CB B.由∠4=∠8,可以推出AD∥BC
C.由∠2=∠6,可以推出AD∥BC D.由∠3=∠7,可以推出AB∥DC
6.(2分)如图,直线 , 被直线 所截,下列说法正确的是( )
A.当 时,一定有
B.当 时,一定有
C.当 时,一定有
D.当 时,一定有
7.(2分)如图,直线a∥b,∠1=50°,∠2=40°,则∠3的度数为( )
A.40° B.90° C.50° D.100°
8.(2分)如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④
C.①③④ D.①②③④ 图4
9.(2分)如图,AB CD,∠ABE= ∠EBF,∠DCE= ∠ECF,设∠ABE=α,∠E=β,∠F=γ,则α,β,γ的数量关系是( )
A.4β﹣α+γ=360° B.3β﹣α+γ=360°
C.4β﹣α﹣γ=360° D.3β﹣2α﹣γ=360°
10.(2分)如图,A、B两点在数轴上表示的数分别为a、b,以下结论:①a﹣b>0;②a+b<0;③(b﹣1)(a+1)>0;④ .其中结论正确的是( )
A.①② B.③④ C.①③ D.①②④
二、填空题(共5题;共5分)
11.(1分)比较大小: 3(填“>”、“<”或“=”)
12.(1分)如图,AB//CD, 则
13.(1分)如图所示是一个数值转换机的示意图,当最后输出的结果是26时,则开始输入的x的数值为 .
14.(1分)计算: .
15.(1分)若 , , ,则 的大小关系用“<”号排列为 .
三、计算题(共2题;共15分)
16.(5分)计算 .
17.(10分)求下列各式中x的值.
(1)(5分)4 (x-1) 2=25
(2)(5分) (x+2) 2=7
四、解答题(共10题;共60分)
18.(5分)如图,若 , , ,求 的度数.
19.(5分)若一正数a的两个平方根分别是2m-3和5-m,求a的值.
20.(10分)(1)(5分)计算:
①
②
(2)(5分)求方程中的的值
①
②
21.(7分)已知:如图,DE⊥AC,垂足为点E,∠AGF=∠ABC,∠BFG+∠BDE=180°,
求证:BF⊥AC.
请完成下面的证明的过程,并在括号内注明理由.
证明:∵∠AGF=∠ABC(已知)
∴FG∥ ( )
∴∠BFG=∠FBC( )
∵∠BFG+∠BDE=180°(已知)
∴∠FBC+∠BDE=180°( )
∴BF∥DE( )
∴∠BFA= (两直线平行,同位角相等)
∵DE⊥AC(已知)
∴∠DEA=90°( )
∴∠BFA=90°(等量代换)
∴BF⊥AC(垂直的定义)
22.(5分)如图,∠A=50°,∠DBC=40°,AD∥BC,BD⊥DC.判断AB与CD的位置关系,并说明理由.
23.(5分)如图,DE⊥BC,AF⊥BC,∠1+∠2=180°.求证:∠FGA+∠CAB=180°
24.(9分)如图,AB与EF交于点B,CD与EF交于点D,根据图形,请补全下面这道题的解答过程.
(1)(1分)∵∠1=∠2(已知)
∴ CD( )
∴∠ABD+∠CDB = ( )
(2)(1分)∵∠BAC =65°,∠ACD=115°,( 已知 )
∴∠BAC+∠ACD=180° (等式性质)
∴AB CD ( )
(3)(1分)∵CD⊥AB于D,EF⊥AB于F,∠BAC=55°(已知)
∴∠ABD=∠CDF=90°( 垂直的定义)
∴ (同位角相等,两直线平行)
又∵∠BAC=55°,(已知)
∴∠ACD = ( )
25.(4分)阅读下面求 近似值的方法,回答问题:
①任取正数 ;
②令 则 ;
③ ,则 ;
……以此类推 次,得到
其中 称为 的 阶过剩近似值, 称为 的 阶不足近似值.仿照上述方法,求6的近似值.
①取正数 .
②于是 a2= ;则
③ 的3阶过剩近似值 是 ,3阶不足近似值是
26.(5分)如图 ,AB∥CD,且∠PMQ=2∠QMB,∠PNQ=2∠QND,判断∠P 与∠Q的数量关系,并说明理由.
27.(5分)如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM和∠NOC的度数.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】A
10.【答案】B
11.【答案】<
12.【答案】40°
13.【答案】3或-3
14.【答案】2
15.【答案】a<b<c
16.【答案】解:
17.【答案】(1)解:4(x﹣1)2=25
x﹣1
x 或x
(2)解:整理得:(x+2) 2=14
开方,得:x+2= 或x+2= ,∴x= 或x=
18.【答案】解:如图所示.∵ ,∴∠1=∠2,∴a∥b,∴∠3+∠4=180°.
∵∠3=65°,∴∠4=115°.
19.【答案】一正数a的两个平方根分别是2m-3和5-m,
(2m-3)+(5-m)=0,
m=-2,
2m-3=-7
(-7)2=49
20.【答案】(1)解:①原式=4-4×(-2)
=4+8
=12
②原式=-6-(-3)-(-1)+-(-1)
=
(2)解:①
解得或
②
解得
21.【答案】BC;同位角相等,两直线平行;两直线平行,内错角相等;等量代换;同旁内角互补,两直线平行;∠DEA;垂直的定义.
22.【答案】解:AB∥CD.理由:
∵AD∥BC,
∴∠ADB=∠DBC=40°.
∵BD⊥DC.
∴∠BDC=90°.
∴∠ADC=∠ADB+∠BDC=130°.
∴∠A+∠ADC=180°.
∴AB∥CD.
23.【答案】解:∵DE⊥BC,AF⊥BC,
∴AF∥DE,
∴∠2+∠3=180°.
∵∠1+∠2=180°,
∴∠1=∠3,
∴GF∥AC,
∴∠FGA+∠CAB=180°.
24.【答案】(1)AB;内错角相等,两直线平行;180°;两直线平行,同旁内角互补
(2)同旁内角互补,两直线平行
(3)AB;CD;125°;两直线平行,同旁内角互补
25.【答案】;;;
26.【答案】解:作QR∥AB,PL∥AB,∴RQ∥CD∥AB,PL∥AB∥CD
∴∠RQM=∠BMQ,∠RQN=∠QND,∠MPL=∠BMP,∠NPL=∠PND,
∵∠PMQ=2∠QMB,∠PNQ=2∠QND ,
∴∠PMB=3∠QMB ,∠PND=3∠QND ,
∵∠MQN=∠∠RQM+∠RQN=∠BMQ+∠QND,
∠MPN=∠MPL+∠NPL=∠BMP+∠PND,
∴∠MPN=3∠MQN,即∠P=3∠Q.
27.【答案】解:∵OE平分∠BON,
∴∠BON=2∠EON=2×20°=40°,
∴∠NOC=180°﹣∠BON=180°﹣40°=140°,
∠MOC=∠BON=40°,
∵AO⊥BC,
∴∠AOC=90°,
∴∠AOM=∠AOC﹣∠MOC=90°﹣40°=50°,
所以∠NOC=140°,∠AOM=50°.
