高中物理 人教版2019必修第二册 单元测试 第八章 机械能守恒定律 (含答案)
文档属性
| 名称 | 高中物理 人教版2019必修第二册 单元测试 第八章 机械能守恒定律 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 406.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-18 19:59:32 | ||
图片预览



文档简介
第八章 机械能守恒定律
章节达标检测 考试试卷
注意事项:1.本试卷满分100分,考试用时75分钟。2.无特殊说明,本试卷中重力加速度g取10 m/s2。
一、选择题(本题共12小题,每小题3分,共36分。每小题只有一个选项符合题目要求)
1.2021年7月30日,东京奥运会女子蹦床决赛,朱雪莹以56.635分夺得金牌。在做蹦床运动时,由高处自由落下,从朱雪莹双脚接触蹦床开始到最低点的过程中,关于蹦床的弹性势能、运动员的重力势能的变化情况,下列说法正确的是 ( )
A.增大、增大 B.增大、减小
C.减小、增大 D.减小、减小
2.如图所示,质量为50 kg的同学在做仰卧起坐。若该同学上半身的质量约为全身质量的,她在1 min内做了50个仰卧起坐,每次上半身重心上升的距离均为0.3 m,则她在1 min内克服重力做的功W和相应的功率P约为 ( )
A.4 500 J 75 W B.450 J 7.5 W
C.3 600 J 60 W D.360 J 6 W
3.机车在运行过程中所受的阻力大小始终不变,在某一段直线轨道上匀加速运动,达到最大功率后保持功率恒定直到达到最大速度的过程中,下列说法正确的是 ( )
A.机车达到最大速度时牵引力最小
B.机车一直匀加速运动直到达到最大速度
C.匀加速过程中任意相等时间内牵引力做功相等
D.在功率恒定的加速阶段,相等时间内机车动能变化相同
4.如图所示,小球以初速度v0=4 m/s从A点沿不光滑的轨道运动到B点后自动返回,其返回途中经过A点时速度大小为2 m/s,小球可视为质点,则A、B两点的高度差h为 ( )
A.0.3 m B.0.4 m C.0.5 m D.0.6 m
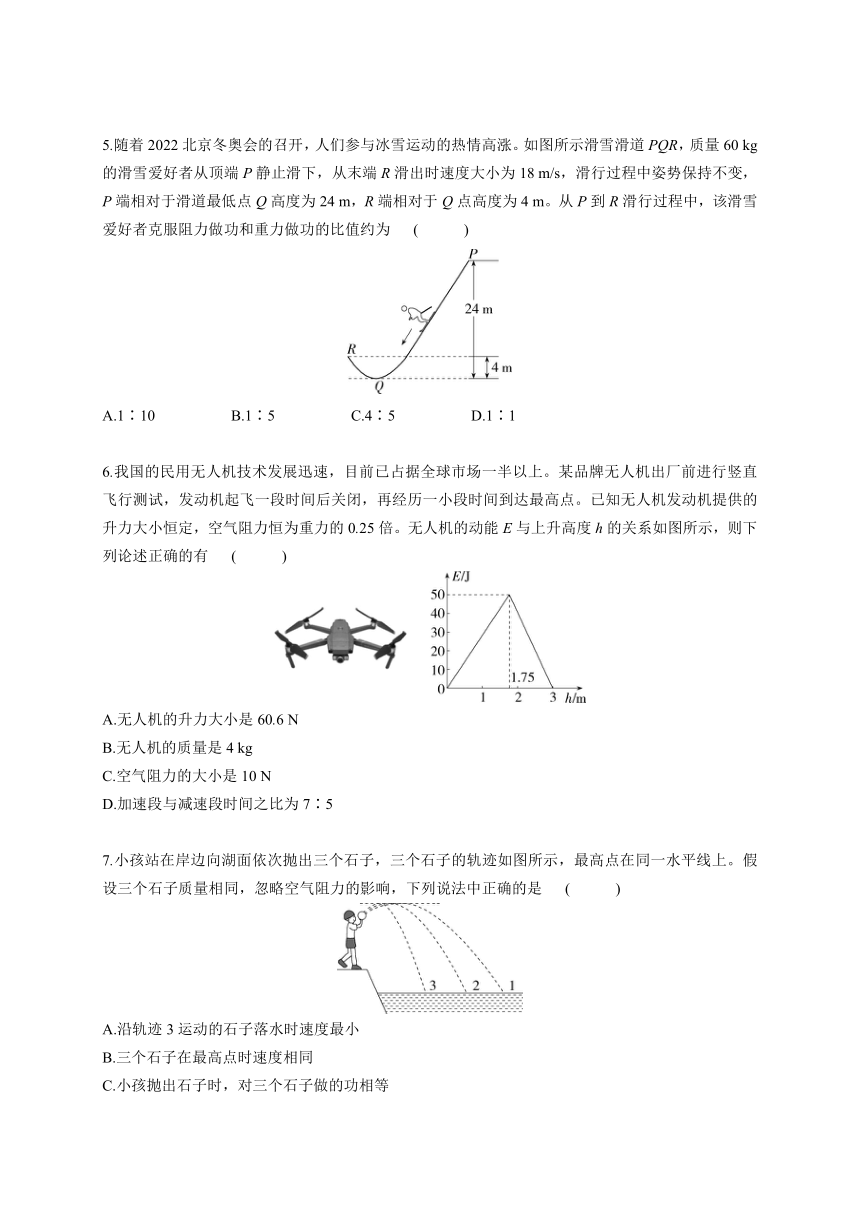
5.随着2022北京冬奥会的召开,人们参与冰雪运动的热情高涨。如图所示滑雪滑道PQR,质量60 kg的滑雪爱好者从顶端P静止滑下,从末端R滑出时速度大小为18 m/s,滑行过程中姿势保持不变,P端相对于滑道最低点Q高度为24 m,R端相对于Q点高度为4 m。从P到R滑行过程中,该滑雪爱好者克服阻力做功和重力做功的比值约为 ( )
A.1∶10 B.1∶5 C.4∶5 D.1∶1
6.我国的民用无人机技术发展迅速,目前已占据全球市场一半以上。某品牌无人机出厂前进行竖直飞行测试,发动机起飞一段时间后关闭,再经历一小段时间到达最高点。已知无人机发动机提供的升力大小恒定,空气阻力恒为重力的0.25倍。无人机的动能E与上升高度h的关系如图所示,则下列论述正确的有 ( )
A.无人机的升力大小是60.6 N
B.无人机的质量是4 kg
C.空气阻力的大小是10 N
D.加速段与减速段时间之比为7∶5
7.小孩站在岸边向湖面依次抛出三个石子,三个石子的轨迹如图所示,最高点在同一水平线上。假设三个石子质量相同,忽略空气阻力的影响,下列说法中正确的是 ( )
A.沿轨迹3运动的石子落水时速度最小
B.三个石子在最高点时速度相同
C.小孩抛出石子时,对三个石子做的功相等
D.沿轨迹3运动的石子在落水时重力的功率最大
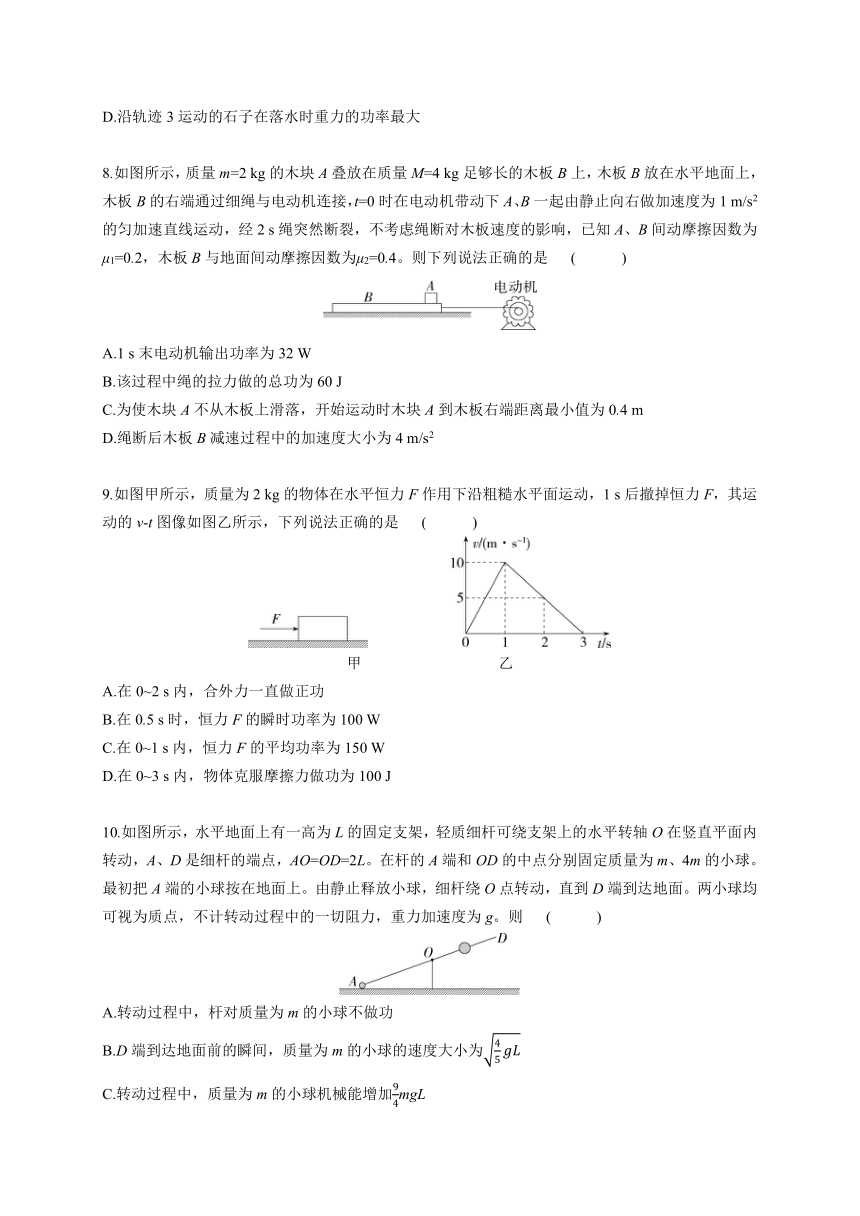
8.如图所示,质量m=2 kg的木块A叠放在质量M=4 kg足够长的木板B上,木板B放在水平地面上,木板B的右端通过细绳与电动机连接,t=0时在电动机带动下A、B一起由静止向右做加速度为1 m/s2的匀加速直线运动,经2 s绳突然断裂,不考虑绳断对木板速度的影响,已知A、B间动摩擦因数为μ1=0.2,木板B与地面间动摩擦因数为μ2=0.4。则下列说法正确的是 ( )
A.1 s末电动机输出功率为32 W
B.该过程中绳的拉力做的总功为60 J
C.为使木块A不从木板上滑落,开始运动时木块A到木板右端距离最小值为0.4 m
D.绳断后木板B减速过程中的加速度大小为4 m/s2
9.如图甲所示,质量为2 kg的物体在水平恒力F作用下沿粗糙水平面运动,1 s后撤掉恒力F,其运动的v-t图像如图乙所示,下列说法正确的是 ( )
甲 乙
A.在0~2 s内,合外力一直做正功
B.在0.5 s时,恒力F的瞬时功率为100 W
C.在0~1 s内,恒力F的平均功率为150 W
D.在0~3 s内,物体克服摩擦力做功为100 J
10.如图所示,水平地面上有一高为L的固定支架,轻质细杆可绕支架上的水平转轴O在竖直平面内转动,A、D是细杆的端点,AO=OD=2L。在杆的A端和OD的中点分别固定质量为m、4m的小球。最初把A端的小球按在地面上。由静止释放小球,细杆绕O点转动,直到D端到达地面。两小球均可视为质点,不计转动过程中的一切阻力,重力加速度为g。则 ( )
A.转动过程中,杆对质量为m的小球不做功
B.D端到达地面前的瞬间,质量为m的小球的速度大小为
C.转动过程中,质量为m的小球机械能增加mgL
D.转动过程中,杆对质量为4m的小球做功-3mgL
11.如图所示,一轻弹簧下端固定在倾角为θ的固定斜面底端,弹簧处于原长时上端位于斜面上B点,B点以上斜面光滑,B点到斜面底端粗糙,可视为质点的物体质量为m,从A点静止释放,将弹簧压缩到最短后恰好能被弹回到B点。已知A、B间的距离为L,物体与B点以下斜面间的动摩擦因数为μ,重力加速度为g,不计空气阻力,则此过程中 ( )
A.物体克服摩擦力做的功为mgL sin θ
B.弹簧的最大压缩量为
C.物体的最大动能一定等于mgL sin θ
D.弹簧弹性势能的最大值为mgL sin θ·
12.如图所示,倾斜放置的传送带AB长为10 m,在电机驱动下以大小为v=3 m/s的恒定速率顺时针转动,传送带的倾角θ=37°,一个质量为2 kg的物块轻放在传送带A端,同时给物块施加一个沿斜面向上的恒定拉力F,物块先加速后匀速从A端运动到B端,物块运动的时间为4 s,物块与传送带之间的动摩擦因数为0.5,sin 37°=0.6,cos 37°=0.8,最大静摩擦力等于滑动摩擦力,则在物块向上运动过程中,下列说法不正确的是 ( )
A.拉力对物块做的功为9 J
B.物块加速运动的时间为 s
C.因传送物块电机多消耗的电能为60 J
D.物块与传送带之间,因摩擦产生的热量为16 J
二、非选择题(本题共6小题,共64分)
13.(6分)在用打点计时器验证机械能守恒定律的实验中,使质量为m=1.00 kg的重物自由下落,打点计时器在纸带上打出一系列的点,选取一条符合实验要求的纸带,如图1所示。O为打下的第一个点,A、B、C为从合适位置开始选取的连续点中的三个点。已知打点计时器每隔0.02 s打一个点,当地的重力加速度g=9.80 m/s2,那么:
图1 图2
(1)根据图1中所给的数据,应取图中O点到 点来验证机械能守恒定律。
(2)从O点到(1)问中所取的点,对应的重物重力势能的减少量ΔEp= J,动能增加量ΔEk= J。(结果保留三位有效数字)
(3)若测出纸带上所有点到O点的距离,根据纸带算出各点的速度v及重物下落的高度h,则以为纵轴、以h为横轴画出的图像是图2中的 。
14.(8分)“用DIS验证机械能守恒定律”实验装置如图1。
图1 图2
(1)本实验利用 传感器测量摆锤释放后经过各个点的速度,结合各挡光片相对轨道最低点的 和摆锤质量,可以分析摆锤运动过程中机械能的变化。
(2)将摆锤由A点静止释放,在摆锤摆到最低点的过程中 ( )
A.连接杆拉力不做功,合外力不做功
B.连接杆拉力不做功,合外力做正功
C.连接杆拉力做正功,合外力不做功
D.连接杆拉力做正功,合外力做正功
(3)根据实验结果绘制的图像如图2所示,图像的横轴表示摆锤距离最低点的高度,纵轴表示摆锤的重力势能、动能或机械能。其中表示摆锤的重力势能、动能的图线分别是 和 。(选填“甲”“乙”或“丙”)
(4)根据实验图像,可以得出的结论是 。
15.(12分)如图甲所示,在水平路段AB上有一质量为2×103 kg的汽车,正以10 m/s的速度向右匀速运动,汽车前方的水平路段BC较粗糙,汽车通过整个ABC路段的v-t图像如图乙所示(在t=15 s处,水平虚线与曲线相切),运动过程中汽车发动机的输出功率保持20 kW不变,假设汽车在两个路段受到的阻力各自有恒定大小。求:
(1)汽车在AB路段上运动时所受的阻力Ff1;
(2)汽车到达B点时的加速度a;
(3)BC路段的长度。
甲 乙
16.(12分)如图所示,长L=1.5 m的轻杆左端套在固定的光滑水平转轴O上,右端连接质量mA=3 kg的小球A,绕过光滑定滑轮的细线一端连接A,另一端连接质量mB=1 kg的小球B,为使轻杆保持水平,B受到竖直向下的拉力F。已知C、A间的细线竖直且长度l=0.5 m,细线足够长,重力加速度大小为g。现撤去拉力F,求:
(1)撤去F的瞬间,轻杆对A的弹力大小T1和细线对A的弹力大小T2;
(2)A运动到O点正下方时,A和B的速度大小之比vA∶vB;
(3)A从图示位置运动到O点正下方的过程中,细线对A所做的功W。
17.(12分)如图甲所示,一根轻质弹簧上端固定在天花板上,下端挂一小球(可视为质点),弹簧处于原长时小球位于O点。将小球从O点由静止释放,小球沿竖直方向在OP之间做往复运动,如图乙所示。小球运动过程中弹簧始终处于弹性限度内。不计空气阻力,重力加速度为g。
(1)在小球运动的过程中,经过某一位置A时动能为Ek1,重力势能为Ep1,弹簧弹性势能为E弹1,经过另一位置B时动能为Ek2,重力势能为Ep2,弹簧弹性势能为E弹2。请根据功是能量转化的量度,证明:小球由A运动到B的过程中,小球、弹簧和地球组成的物体系统机械能守恒。
(2)已知弹簧劲度系数为k,以O点为坐标原点,竖直向下为x轴正方向,建立一维坐标系O-x,如图乙所示。
a.请在图丙中画出小球从O运动到P的过程中,弹簧弹力的大小F随相对于O点的位移x变化的图像。根据F-x图像求小球从O运动到任意位置x的过程中弹力所做的功W,以及小球在此位置时弹簧的弹性势能E弹(设弹簧在原长时弹性势能为0)。
b.已知小球质量为m,求小球运动过程中瞬时速度最大值的大小v。
18.(14分)如图所示,质量为m=1 kg的小物块从光滑斜面上的A点由静止下滑,进入圆心为O、半径为R=1 m的光滑圆弧轨道BCD(B点和D点等高)。圆弧B点的切线与斜面重合,DE为光滑曲线轨道(该轨道与物体以某一速度从E点平抛后的运动轨迹重合),光滑曲线轨道DE在D点处的切线与OD垂直,曲线轨道的E端与带有挡板的光滑水平木板平滑连接,轻质弹簧左端固定在挡板上。已知A点距斜面底端B的距离l=2 m,水平木板距离地面的高度h=0.45 m,斜面的倾角θ=37°。(已知sin 37°=0.6,cos 37°=0.8)求:
(1)小物块运动到圆弧最低点C时受到的支持力的大小FN;
(2)要使小物块从D点沿轨道运动到E点的过程中对轨道刚好没有压力,小物块释放点距B点的距离d(计算结果保留两位有效数字);
(3)若斜面不光滑且小物块与斜面之间的动摩擦因数μ=0.1,小物块仍从A点下滑,在整个过程中小物块沿斜面滑行的总路程s。
答案全解全析
1.B 从朱雪莹双脚接触蹦床开始到最低点的过程中,蹦床的形变量逐渐增大,故蹦床的弹性势能逐渐增大;朱雪莹的高度逐渐降低,故朱雪莹的重力势能逐渐减小,选B。
2.A 每次上半身重心上升的距离均为0.3 m,则她每一次克服重力做的功约为W1=mgh=×50×10×0.3 J=90 J,1分钟内克服重力所做的功约为W=50W1=50×90 J=4 500 J,平均功率约为P== W=75 W,故选A。
3.A 当功率达到额定功率后,机车的功率就不再增大,要增大速度,就要减小牵引力,当牵引力等于阻力时,机车速度达到最大值,所以机车匀加速运动过程达不到最大速度,故A正确,B错误;机车匀加速过程中,牵引力大小不变,任意相等时间内机车的位移大小不同,则牵引力做功不相等,C错误;在功率恒定的加速阶段,由W=Pt知相等时间内机车牵引力做功相等,但阻力做功不相等,则机车动能变化不相同,D错误。
4.C 设小球从A点到B点的过程中克服摩擦力做功为Wf,则对小球从A点到B点的过程应用动能定理有-mgh-Wf=0-m,对小球从B点回到A点的过程应用动能定理有mgh-Wf=mv2-0,可得h=0.5 m,选C。
5.B 由能量守恒可知从P到R滑行过程中,该滑雪爱好者克服阻力做的功Wf=mg(H-h)-mv2,解得Wf=60×10×(24-4) J-×60×182 J=2 280 J,从P到R滑行过程中,重力做功WG=mg(H-h)=12 000 J,则=≈,故选B。
6.D 由动能E与上升高度h的关系图线,可得斜率大小即合外力的大小,故得到加速段的合外力大小为F-mg-f≈28.6 N,减速段的合外力为mg+f=40 N,联立可得升力F=68.6 N,故A错误;由减速段的合外力为mg+f=1.25mg=40 N,可得无人机的质量m=3.2 kg,空气阻力f=0.25mg=8 N,故B、C错误;由于加速段和减速段均为匀变速直线运动,可知两阶段的平均速度相等,故时间之比等于位移之比,为1.75∶1.25=7∶5,故D正确。
7.A 设任一石子初速度大小为v0,初速度的竖直分量为vy,水平分量为vx,初速度与水平方向的夹角为α,上升的高度为h,向上运动时间为t,落水时速度为v。取竖直向上为正方向,从抛出至到达最高点,由0-=-2gh,得vy=,由题可知h相同,所以三个石子初速度的竖直分量vy相同,由vy=v0 sin α可知,由于角α不同,所以v0不同,沿轨迹1抛出的石子的初速度最大,沿轨迹3抛出的石子的初速度最小。石子从抛出到落水过程,根据动能定理有WG=mv2-m,得mv2=WG+m,重力做功WG相同,沿轨迹3抛出的石子的初速度最小,所以沿轨迹3运动的石子落水时速度最小,A正确;三个石子在最高点的速度等于抛出时的水平分速度vx,由vx=可知,由于vy相同,初速度与水平方向的夹角α不同,所以vx不同,B错误;在小孩抛出石子过程中,由动能定理得W=m-0,由于沿轨迹1抛出的石子的初速度v0最大,所以小孩对沿轨迹1抛出的石子做功最多,C错误;因三个石子初速度的竖直分量vy相同,则它们落水时竖直方向的分速度也相等,根据P=mgvy,可知重力的功率相等,D错误。
8.B 前2 s内,A、B一起做匀加速直线运动,F-μ2(M+m)g=(M+m)a,代入数据解得F=30 N,1 s末电动机输出功率为P=Fv=F·at1=30 W,故A错误;该过程中绳的拉力做的总功为W=F·a=60 J,故B正确;绳断后木板B减速过程中的加速度大小为a2==5 m/s2,故D错误;绳断时A、B的速度均为v=at2=2 m/s,若木块A没有从木板上滑落,则之后A向右运动的位移xA===1 m,B向右运动的位移xB==0.4 m,Δx=xA-xB=0.6 m,为使木块A不从木板上滑落,开始运动时木块A到木板右端的距离最小值为0.6 m,故C错误。
9.C 0~1 s内,速度增加,根据动能定理知,合力做正功,1~3 s内,速度减小,根据动能定理知,合力做负功,故A错误;根据v-t图线知,匀加速运动的加速度大小a1=10 m/s2,匀减速运动的加速度大小a2= m/s2=5 m/s2,根据牛顿第二定律得f=ma2,F-f=ma1,解得f=10 N,F=30 N,由图知0.5 s时,速度为5 m/s,则恒力F的瞬时功率为P=Fv=30×5 W=150 W,故B错误;0~1 s内,平均速度等于0.5 s时的瞬时速度5 m/s,恒力F的平均功率为=F=30×5 W=150 W,故C正确;0~3 s内,物体的位移大小x=×3×10 m=15 m,克服摩擦力做功Wf=fx=10×15 J=150 J,故D错误。
10.D 转动过程中,质量为m的小球受到的重力做负功,而动能增加,可知,杆对质量为m的小球做正功,故A错误;两小球同轴转动,角速度相同,则有=,v1=2v2,D端到达地面前的瞬间,根据机械能守恒有4mgL-mg×2L=m+×4m,解得v1=,v2=,故B错误;转动过程中,质量为m的小球,动能增加量Ek=m=mgL,重力势能增加量Ep=mg×2L,机械能增加量E=Ek+Ep=3mgL,故C错误;两小球组成的系统机械能守恒,质量为m的小球机械能增加3mgL,则质量为4m的小球机械能减小3mgL,其机械能变化是由于杆对其做功引起的,故杆对质量为4m的小球做功-3mgL,故D正确。
11.A 对于物体运动的整个过程,运用动能定理得mgL sin θ-Wf=0,则物体克服摩擦力做的功Wf=mgL sin θ,故A正确。物体从A运动到B过程机械能守恒,可得物体刚接触弹簧时的动能等于mgL sin θ。若μ≥tan θ,则μmg cos θ≥mg sin θ,物体在B点达到最大动能mgL sin θ;若μ12.A 物块开始时做初速度为零的匀加速直线运动,根据牛顿第二定律可得F+μmg cos θ-mg sin θ=ma,当物块与传送带速度相等时,物块做匀速运动,有+v=L,解得F=8.5 N,a=2.25 m/s2,拉力对物块做的功为WF=FL=85 J,物块加速运动的时间为t1== s,故A说法错误,B说法正确;物块与传送带间的相对位移为s=vt1-=2 m,根据功能关系,可得因摩擦产生的热量为Q=μmg cos θ·s=16 J,故D说法正确;物块加速过程中的摩擦力为滑动摩擦力,即f1=μmg cos 37°=8 N,物块匀速运动过程的摩擦力为静摩擦,f2=mg sin 37°-F=3.5 N,两摩擦力均沿传送带向上,则因传送物块电机多消耗的电能用来克服摩擦力做功,W=f1vt1+f2v(t-t1),解得W=60 J,故C说法正确。
13.答案 (1)B(1分) (2)1.88(2分) 1.84(2分) (3)A(1分)
解析 (1)实验需要验证重物重力势能的减少量与动能的增加量相等,需要求出重物的速度,根据题图1结合匀变速直线运动的推论可以求出打B点时重物的瞬时速度,因此应取图中O点到B点来验证机械能守恒定律。
(2)从O点到B点,对应的重物重力势能的减少量
ΔEp=mg·OB=1.00×9.80×19.20×10-2 J≈1.88 J
打B点时重物的瞬时速度为
vB== m/s=1.92 m/s
从O点到B点,对应的重物动能增加量
ΔEk=m=×1.00×1.922 J≈1.84 J
(3)重物下落过程,由机械能守恒定律得mgh=mv2,整理得=gh,g是定值,则与h成正比,故选A。
14.答案 (1)光电(1分) 高度(1分) (2)B(2分) (3)乙(1分) 丙(1分) (4)摆锤运动过程中机械能守恒(2分)
解析 (1)本实验利用光电传感器测量摆锤释放后经过各个点的速度,结合各挡光片相对轨道最低点的高度和摆锤质量,可以分析摆锤运动过程中机械能的变化。
(2)将摆锤由A点静止释放,在摆锤摆到最低点的过程中,连接杆拉力方向始终垂直于摆锤的速度方向,所以不做功,而摆锤的动能增大,合外力做正功,故选B。
(3)摆锤的重力势能随h的增大而增大,动能随h的增大而减小,所以其中表示摆锤的重力势能、动能的图线分别是乙和丙。
(4)图2中甲图线表示摆锤运动过程中的机械能,在实验误差允许的范围内图线甲平行于h轴,由此可以得出的结论是摆锤运动过程中机械能守恒。
15.答案 (1)2 000 N (2)-1 m/s2 (3)68.75 m
解析 (1)汽车在AB路段做匀速直线运动,有
F1=Ff1 (1分)
P=F1v1 (1分)
所以Ff1==2 000 N(1分)
(2)t=15 s时汽车处于平衡状态,有
F2=Ff2 (1分)
P=F2v2 (1分)
所以Ff2==4 000 N(1分)
t=5 s时汽车开始做减速运动,有
F1-Ff2=ma (1分)
解得a=-1 m/s2 (1分)
(3)汽车在BC段运动时,由动能定理得
PΔt-Ff2x=m-m (2分)
解得x=68.75 m(2分)
16.答案 (1)0 15 N (2)5∶3 (3)-22.7 J
解析 (1)撤去F的瞬间,轻杆弹力提供A的向心力,A的速度为零,因此向心力为零,即T1=0 (1分)
对A有mAg-T2=mAa (1分)
对B有T2-mBg=mBa (1分)
解得T2=15 N(1分)
(2)小球A运动到O点正下方时,设细线与竖直方向的夹角为θ,则tan θ==,故θ=37°,可得sin θ=,将小球A的速度沿细线方向与垂直于细线方向分解,可得vB=vA sin θ (3分)
解得vA∶vB=5∶3 (1分)
(3)对A、B及细线组成的系统,机械能守恒,有
mAgL-mBg(-l)=mA+mB (2分)
对小球A,由动能定理得mAgL+W=mA (1分)
解得W≈-22.7 J(1分)
17.答案 (1)见解析 (2)a.图见解析 -kx2 kx2 b.g
解析 (1)设重力做的功为WG,弹力做的功为W弹,根据动能定理有
WG+W弹=Ek2-Ek1 (2分)
由重力做功与重力势能的关系有WG=Ep1-Ep2 (1分)
由弹力做功与弹性势能的关系有W弹=E弹1-E弹2 (1分)
联立以上三式可得Ek1+Ep1+E弹1=Ek2+Ep2+E弹2 (1分)
(2)
a.F-x图像如图所示,图中的图线和x轴围成的面积表示弹力做功的大小。 (1分)
所以弹力做功为W=-kx2 (1分)
由弹力做功与弹性势能的关系有W弹=0-E弹 (1分)
解得E弹=kx2 (1分)
b.小球由O点到P点过程中,当弹力等于重力时小球有最大速度,此时有mg=kx (1分)
根据动能定理有mgx-kx2=mv2-0 (1分)
解得v=g (1分)
18.答案 (1)38 N (2)2.1 m (3)15 m
解析 (1)由A→C过程,根据动能定理有mg[l sin θ+R(1- cos θ)]=m (2分)
根据牛顿第二定律有FN-mg= (2分)
解得FN=38 N(1分)
(2)要使物块由D点运动到E点对轨道没有压力作用,看作物块由D到E做平抛运动的逆运动,即物块运动到E点时的速度为平抛运动的初速度,运动到D点时,根据平抛运动规律有tan θ= (1分)
=2gh (1分)
解得v0=4 m/s,vy=3 m/s
则vD==5 m/s(1分)
小物块从释放点运动到D点的过程,根据动能定理有
mgd sin θ=m (2分)
解得d= m≈2.1 m(1分)
(3)从开始下滑到运动到B点的速度为零时,根据动能定理有
mgl sin θ-μmgs cos θ=0 (2分)
解得s=15 m(1分)
章节达标检测 考试试卷
注意事项:1.本试卷满分100分,考试用时75分钟。2.无特殊说明,本试卷中重力加速度g取10 m/s2。
一、选择题(本题共12小题,每小题3分,共36分。每小题只有一个选项符合题目要求)
1.2021年7月30日,东京奥运会女子蹦床决赛,朱雪莹以56.635分夺得金牌。在做蹦床运动时,由高处自由落下,从朱雪莹双脚接触蹦床开始到最低点的过程中,关于蹦床的弹性势能、运动员的重力势能的变化情况,下列说法正确的是 ( )
A.增大、增大 B.增大、减小
C.减小、增大 D.减小、减小
2.如图所示,质量为50 kg的同学在做仰卧起坐。若该同学上半身的质量约为全身质量的,她在1 min内做了50个仰卧起坐,每次上半身重心上升的距离均为0.3 m,则她在1 min内克服重力做的功W和相应的功率P约为 ( )
A.4 500 J 75 W B.450 J 7.5 W
C.3 600 J 60 W D.360 J 6 W
3.机车在运行过程中所受的阻力大小始终不变,在某一段直线轨道上匀加速运动,达到最大功率后保持功率恒定直到达到最大速度的过程中,下列说法正确的是 ( )
A.机车达到最大速度时牵引力最小
B.机车一直匀加速运动直到达到最大速度
C.匀加速过程中任意相等时间内牵引力做功相等
D.在功率恒定的加速阶段,相等时间内机车动能变化相同
4.如图所示,小球以初速度v0=4 m/s从A点沿不光滑的轨道运动到B点后自动返回,其返回途中经过A点时速度大小为2 m/s,小球可视为质点,则A、B两点的高度差h为 ( )
A.0.3 m B.0.4 m C.0.5 m D.0.6 m
5.随着2022北京冬奥会的召开,人们参与冰雪运动的热情高涨。如图所示滑雪滑道PQR,质量60 kg的滑雪爱好者从顶端P静止滑下,从末端R滑出时速度大小为18 m/s,滑行过程中姿势保持不变,P端相对于滑道最低点Q高度为24 m,R端相对于Q点高度为4 m。从P到R滑行过程中,该滑雪爱好者克服阻力做功和重力做功的比值约为 ( )
A.1∶10 B.1∶5 C.4∶5 D.1∶1
6.我国的民用无人机技术发展迅速,目前已占据全球市场一半以上。某品牌无人机出厂前进行竖直飞行测试,发动机起飞一段时间后关闭,再经历一小段时间到达最高点。已知无人机发动机提供的升力大小恒定,空气阻力恒为重力的0.25倍。无人机的动能E与上升高度h的关系如图所示,则下列论述正确的有 ( )
A.无人机的升力大小是60.6 N
B.无人机的质量是4 kg
C.空气阻力的大小是10 N
D.加速段与减速段时间之比为7∶5
7.小孩站在岸边向湖面依次抛出三个石子,三个石子的轨迹如图所示,最高点在同一水平线上。假设三个石子质量相同,忽略空气阻力的影响,下列说法中正确的是 ( )
A.沿轨迹3运动的石子落水时速度最小
B.三个石子在最高点时速度相同
C.小孩抛出石子时,对三个石子做的功相等
D.沿轨迹3运动的石子在落水时重力的功率最大
8.如图所示,质量m=2 kg的木块A叠放在质量M=4 kg足够长的木板B上,木板B放在水平地面上,木板B的右端通过细绳与电动机连接,t=0时在电动机带动下A、B一起由静止向右做加速度为1 m/s2的匀加速直线运动,经2 s绳突然断裂,不考虑绳断对木板速度的影响,已知A、B间动摩擦因数为μ1=0.2,木板B与地面间动摩擦因数为μ2=0.4。则下列说法正确的是 ( )
A.1 s末电动机输出功率为32 W
B.该过程中绳的拉力做的总功为60 J
C.为使木块A不从木板上滑落,开始运动时木块A到木板右端距离最小值为0.4 m
D.绳断后木板B减速过程中的加速度大小为4 m/s2
9.如图甲所示,质量为2 kg的物体在水平恒力F作用下沿粗糙水平面运动,1 s后撤掉恒力F,其运动的v-t图像如图乙所示,下列说法正确的是 ( )
甲 乙
A.在0~2 s内,合外力一直做正功
B.在0.5 s时,恒力F的瞬时功率为100 W
C.在0~1 s内,恒力F的平均功率为150 W
D.在0~3 s内,物体克服摩擦力做功为100 J
10.如图所示,水平地面上有一高为L的固定支架,轻质细杆可绕支架上的水平转轴O在竖直平面内转动,A、D是细杆的端点,AO=OD=2L。在杆的A端和OD的中点分别固定质量为m、4m的小球。最初把A端的小球按在地面上。由静止释放小球,细杆绕O点转动,直到D端到达地面。两小球均可视为质点,不计转动过程中的一切阻力,重力加速度为g。则 ( )
A.转动过程中,杆对质量为m的小球不做功
B.D端到达地面前的瞬间,质量为m的小球的速度大小为
C.转动过程中,质量为m的小球机械能增加mgL
D.转动过程中,杆对质量为4m的小球做功-3mgL
11.如图所示,一轻弹簧下端固定在倾角为θ的固定斜面底端,弹簧处于原长时上端位于斜面上B点,B点以上斜面光滑,B点到斜面底端粗糙,可视为质点的物体质量为m,从A点静止释放,将弹簧压缩到最短后恰好能被弹回到B点。已知A、B间的距离为L,物体与B点以下斜面间的动摩擦因数为μ,重力加速度为g,不计空气阻力,则此过程中 ( )
A.物体克服摩擦力做的功为mgL sin θ
B.弹簧的最大压缩量为
C.物体的最大动能一定等于mgL sin θ
D.弹簧弹性势能的最大值为mgL sin θ·
12.如图所示,倾斜放置的传送带AB长为10 m,在电机驱动下以大小为v=3 m/s的恒定速率顺时针转动,传送带的倾角θ=37°,一个质量为2 kg的物块轻放在传送带A端,同时给物块施加一个沿斜面向上的恒定拉力F,物块先加速后匀速从A端运动到B端,物块运动的时间为4 s,物块与传送带之间的动摩擦因数为0.5,sin 37°=0.6,cos 37°=0.8,最大静摩擦力等于滑动摩擦力,则在物块向上运动过程中,下列说法不正确的是 ( )
A.拉力对物块做的功为9 J
B.物块加速运动的时间为 s
C.因传送物块电机多消耗的电能为60 J
D.物块与传送带之间,因摩擦产生的热量为16 J
二、非选择题(本题共6小题,共64分)
13.(6分)在用打点计时器验证机械能守恒定律的实验中,使质量为m=1.00 kg的重物自由下落,打点计时器在纸带上打出一系列的点,选取一条符合实验要求的纸带,如图1所示。O为打下的第一个点,A、B、C为从合适位置开始选取的连续点中的三个点。已知打点计时器每隔0.02 s打一个点,当地的重力加速度g=9.80 m/s2,那么:
图1 图2
(1)根据图1中所给的数据,应取图中O点到 点来验证机械能守恒定律。
(2)从O点到(1)问中所取的点,对应的重物重力势能的减少量ΔEp= J,动能增加量ΔEk= J。(结果保留三位有效数字)
(3)若测出纸带上所有点到O点的距离,根据纸带算出各点的速度v及重物下落的高度h,则以为纵轴、以h为横轴画出的图像是图2中的 。
14.(8分)“用DIS验证机械能守恒定律”实验装置如图1。
图1 图2
(1)本实验利用 传感器测量摆锤释放后经过各个点的速度,结合各挡光片相对轨道最低点的 和摆锤质量,可以分析摆锤运动过程中机械能的变化。
(2)将摆锤由A点静止释放,在摆锤摆到最低点的过程中 ( )
A.连接杆拉力不做功,合外力不做功
B.连接杆拉力不做功,合外力做正功
C.连接杆拉力做正功,合外力不做功
D.连接杆拉力做正功,合外力做正功
(3)根据实验结果绘制的图像如图2所示,图像的横轴表示摆锤距离最低点的高度,纵轴表示摆锤的重力势能、动能或机械能。其中表示摆锤的重力势能、动能的图线分别是 和 。(选填“甲”“乙”或“丙”)
(4)根据实验图像,可以得出的结论是 。
15.(12分)如图甲所示,在水平路段AB上有一质量为2×103 kg的汽车,正以10 m/s的速度向右匀速运动,汽车前方的水平路段BC较粗糙,汽车通过整个ABC路段的v-t图像如图乙所示(在t=15 s处,水平虚线与曲线相切),运动过程中汽车发动机的输出功率保持20 kW不变,假设汽车在两个路段受到的阻力各自有恒定大小。求:
(1)汽车在AB路段上运动时所受的阻力Ff1;
(2)汽车到达B点时的加速度a;
(3)BC路段的长度。
甲 乙
16.(12分)如图所示,长L=1.5 m的轻杆左端套在固定的光滑水平转轴O上,右端连接质量mA=3 kg的小球A,绕过光滑定滑轮的细线一端连接A,另一端连接质量mB=1 kg的小球B,为使轻杆保持水平,B受到竖直向下的拉力F。已知C、A间的细线竖直且长度l=0.5 m,细线足够长,重力加速度大小为g。现撤去拉力F,求:
(1)撤去F的瞬间,轻杆对A的弹力大小T1和细线对A的弹力大小T2;
(2)A运动到O点正下方时,A和B的速度大小之比vA∶vB;
(3)A从图示位置运动到O点正下方的过程中,细线对A所做的功W。
17.(12分)如图甲所示,一根轻质弹簧上端固定在天花板上,下端挂一小球(可视为质点),弹簧处于原长时小球位于O点。将小球从O点由静止释放,小球沿竖直方向在OP之间做往复运动,如图乙所示。小球运动过程中弹簧始终处于弹性限度内。不计空气阻力,重力加速度为g。
(1)在小球运动的过程中,经过某一位置A时动能为Ek1,重力势能为Ep1,弹簧弹性势能为E弹1,经过另一位置B时动能为Ek2,重力势能为Ep2,弹簧弹性势能为E弹2。请根据功是能量转化的量度,证明:小球由A运动到B的过程中,小球、弹簧和地球组成的物体系统机械能守恒。
(2)已知弹簧劲度系数为k,以O点为坐标原点,竖直向下为x轴正方向,建立一维坐标系O-x,如图乙所示。
a.请在图丙中画出小球从O运动到P的过程中,弹簧弹力的大小F随相对于O点的位移x变化的图像。根据F-x图像求小球从O运动到任意位置x的过程中弹力所做的功W,以及小球在此位置时弹簧的弹性势能E弹(设弹簧在原长时弹性势能为0)。
b.已知小球质量为m,求小球运动过程中瞬时速度最大值的大小v。
18.(14分)如图所示,质量为m=1 kg的小物块从光滑斜面上的A点由静止下滑,进入圆心为O、半径为R=1 m的光滑圆弧轨道BCD(B点和D点等高)。圆弧B点的切线与斜面重合,DE为光滑曲线轨道(该轨道与物体以某一速度从E点平抛后的运动轨迹重合),光滑曲线轨道DE在D点处的切线与OD垂直,曲线轨道的E端与带有挡板的光滑水平木板平滑连接,轻质弹簧左端固定在挡板上。已知A点距斜面底端B的距离l=2 m,水平木板距离地面的高度h=0.45 m,斜面的倾角θ=37°。(已知sin 37°=0.6,cos 37°=0.8)求:
(1)小物块运动到圆弧最低点C时受到的支持力的大小FN;
(2)要使小物块从D点沿轨道运动到E点的过程中对轨道刚好没有压力,小物块释放点距B点的距离d(计算结果保留两位有效数字);
(3)若斜面不光滑且小物块与斜面之间的动摩擦因数μ=0.1,小物块仍从A点下滑,在整个过程中小物块沿斜面滑行的总路程s。
答案全解全析
1.B 从朱雪莹双脚接触蹦床开始到最低点的过程中,蹦床的形变量逐渐增大,故蹦床的弹性势能逐渐增大;朱雪莹的高度逐渐降低,故朱雪莹的重力势能逐渐减小,选B。
2.A 每次上半身重心上升的距离均为0.3 m,则她每一次克服重力做的功约为W1=mgh=×50×10×0.3 J=90 J,1分钟内克服重力所做的功约为W=50W1=50×90 J=4 500 J,平均功率约为P== W=75 W,故选A。
3.A 当功率达到额定功率后,机车的功率就不再增大,要增大速度,就要减小牵引力,当牵引力等于阻力时,机车速度达到最大值,所以机车匀加速运动过程达不到最大速度,故A正确,B错误;机车匀加速过程中,牵引力大小不变,任意相等时间内机车的位移大小不同,则牵引力做功不相等,C错误;在功率恒定的加速阶段,由W=Pt知相等时间内机车牵引力做功相等,但阻力做功不相等,则机车动能变化不相同,D错误。
4.C 设小球从A点到B点的过程中克服摩擦力做功为Wf,则对小球从A点到B点的过程应用动能定理有-mgh-Wf=0-m,对小球从B点回到A点的过程应用动能定理有mgh-Wf=mv2-0,可得h=0.5 m,选C。
5.B 由能量守恒可知从P到R滑行过程中,该滑雪爱好者克服阻力做的功Wf=mg(H-h)-mv2,解得Wf=60×10×(24-4) J-×60×182 J=2 280 J,从P到R滑行过程中,重力做功WG=mg(H-h)=12 000 J,则=≈,故选B。
6.D 由动能E与上升高度h的关系图线,可得斜率大小即合外力的大小,故得到加速段的合外力大小为F-mg-f≈28.6 N,减速段的合外力为mg+f=40 N,联立可得升力F=68.6 N,故A错误;由减速段的合外力为mg+f=1.25mg=40 N,可得无人机的质量m=3.2 kg,空气阻力f=0.25mg=8 N,故B、C错误;由于加速段和减速段均为匀变速直线运动,可知两阶段的平均速度相等,故时间之比等于位移之比,为1.75∶1.25=7∶5,故D正确。
7.A 设任一石子初速度大小为v0,初速度的竖直分量为vy,水平分量为vx,初速度与水平方向的夹角为α,上升的高度为h,向上运动时间为t,落水时速度为v。取竖直向上为正方向,从抛出至到达最高点,由0-=-2gh,得vy=,由题可知h相同,所以三个石子初速度的竖直分量vy相同,由vy=v0 sin α可知,由于角α不同,所以v0不同,沿轨迹1抛出的石子的初速度最大,沿轨迹3抛出的石子的初速度最小。石子从抛出到落水过程,根据动能定理有WG=mv2-m,得mv2=WG+m,重力做功WG相同,沿轨迹3抛出的石子的初速度最小,所以沿轨迹3运动的石子落水时速度最小,A正确;三个石子在最高点的速度等于抛出时的水平分速度vx,由vx=可知,由于vy相同,初速度与水平方向的夹角α不同,所以vx不同,B错误;在小孩抛出石子过程中,由动能定理得W=m-0,由于沿轨迹1抛出的石子的初速度v0最大,所以小孩对沿轨迹1抛出的石子做功最多,C错误;因三个石子初速度的竖直分量vy相同,则它们落水时竖直方向的分速度也相等,根据P=mgvy,可知重力的功率相等,D错误。
8.B 前2 s内,A、B一起做匀加速直线运动,F-μ2(M+m)g=(M+m)a,代入数据解得F=30 N,1 s末电动机输出功率为P=Fv=F·at1=30 W,故A错误;该过程中绳的拉力做的总功为W=F·a=60 J,故B正确;绳断后木板B减速过程中的加速度大小为a2==5 m/s2,故D错误;绳断时A、B的速度均为v=at2=2 m/s,若木块A没有从木板上滑落,则之后A向右运动的位移xA===1 m,B向右运动的位移xB==0.4 m,Δx=xA-xB=0.6 m,为使木块A不从木板上滑落,开始运动时木块A到木板右端的距离最小值为0.6 m,故C错误。
9.C 0~1 s内,速度增加,根据动能定理知,合力做正功,1~3 s内,速度减小,根据动能定理知,合力做负功,故A错误;根据v-t图线知,匀加速运动的加速度大小a1=10 m/s2,匀减速运动的加速度大小a2= m/s2=5 m/s2,根据牛顿第二定律得f=ma2,F-f=ma1,解得f=10 N,F=30 N,由图知0.5 s时,速度为5 m/s,则恒力F的瞬时功率为P=Fv=30×5 W=150 W,故B错误;0~1 s内,平均速度等于0.5 s时的瞬时速度5 m/s,恒力F的平均功率为=F=30×5 W=150 W,故C正确;0~3 s内,物体的位移大小x=×3×10 m=15 m,克服摩擦力做功Wf=fx=10×15 J=150 J,故D错误。
10.D 转动过程中,质量为m的小球受到的重力做负功,而动能增加,可知,杆对质量为m的小球做正功,故A错误;两小球同轴转动,角速度相同,则有=,v1=2v2,D端到达地面前的瞬间,根据机械能守恒有4mgL-mg×2L=m+×4m,解得v1=,v2=,故B错误;转动过程中,质量为m的小球,动能增加量Ek=m=mgL,重力势能增加量Ep=mg×2L,机械能增加量E=Ek+Ep=3mgL,故C错误;两小球组成的系统机械能守恒,质量为m的小球机械能增加3mgL,则质量为4m的小球机械能减小3mgL,其机械能变化是由于杆对其做功引起的,故杆对质量为4m的小球做功-3mgL,故D正确。
11.A 对于物体运动的整个过程,运用动能定理得mgL sin θ-Wf=0,则物体克服摩擦力做的功Wf=mgL sin θ,故A正确。物体从A运动到B过程机械能守恒,可得物体刚接触弹簧时的动能等于mgL sin θ。若μ≥tan θ,则μmg cos θ≥mg sin θ,物体在B点达到最大动能mgL sin θ;若μ
13.答案 (1)B(1分) (2)1.88(2分) 1.84(2分) (3)A(1分)
解析 (1)实验需要验证重物重力势能的减少量与动能的增加量相等,需要求出重物的速度,根据题图1结合匀变速直线运动的推论可以求出打B点时重物的瞬时速度,因此应取图中O点到B点来验证机械能守恒定律。
(2)从O点到B点,对应的重物重力势能的减少量
ΔEp=mg·OB=1.00×9.80×19.20×10-2 J≈1.88 J
打B点时重物的瞬时速度为
vB== m/s=1.92 m/s
从O点到B点,对应的重物动能增加量
ΔEk=m=×1.00×1.922 J≈1.84 J
(3)重物下落过程,由机械能守恒定律得mgh=mv2,整理得=gh,g是定值,则与h成正比,故选A。
14.答案 (1)光电(1分) 高度(1分) (2)B(2分) (3)乙(1分) 丙(1分) (4)摆锤运动过程中机械能守恒(2分)
解析 (1)本实验利用光电传感器测量摆锤释放后经过各个点的速度,结合各挡光片相对轨道最低点的高度和摆锤质量,可以分析摆锤运动过程中机械能的变化。
(2)将摆锤由A点静止释放,在摆锤摆到最低点的过程中,连接杆拉力方向始终垂直于摆锤的速度方向,所以不做功,而摆锤的动能增大,合外力做正功,故选B。
(3)摆锤的重力势能随h的增大而增大,动能随h的增大而减小,所以其中表示摆锤的重力势能、动能的图线分别是乙和丙。
(4)图2中甲图线表示摆锤运动过程中的机械能,在实验误差允许的范围内图线甲平行于h轴,由此可以得出的结论是摆锤运动过程中机械能守恒。
15.答案 (1)2 000 N (2)-1 m/s2 (3)68.75 m
解析 (1)汽车在AB路段做匀速直线运动,有
F1=Ff1 (1分)
P=F1v1 (1分)
所以Ff1==2 000 N(1分)
(2)t=15 s时汽车处于平衡状态,有
F2=Ff2 (1分)
P=F2v2 (1分)
所以Ff2==4 000 N(1分)
t=5 s时汽车开始做减速运动,有
F1-Ff2=ma (1分)
解得a=-1 m/s2 (1分)
(3)汽车在BC段运动时,由动能定理得
PΔt-Ff2x=m-m (2分)
解得x=68.75 m(2分)
16.答案 (1)0 15 N (2)5∶3 (3)-22.7 J
解析 (1)撤去F的瞬间,轻杆弹力提供A的向心力,A的速度为零,因此向心力为零,即T1=0 (1分)
对A有mAg-T2=mAa (1分)
对B有T2-mBg=mBa (1分)
解得T2=15 N(1分)
(2)小球A运动到O点正下方时,设细线与竖直方向的夹角为θ,则tan θ==,故θ=37°,可得sin θ=,将小球A的速度沿细线方向与垂直于细线方向分解,可得vB=vA sin θ (3分)
解得vA∶vB=5∶3 (1分)
(3)对A、B及细线组成的系统,机械能守恒,有
mAgL-mBg(-l)=mA+mB (2分)
对小球A,由动能定理得mAgL+W=mA (1分)
解得W≈-22.7 J(1分)
17.答案 (1)见解析 (2)a.图见解析 -kx2 kx2 b.g
解析 (1)设重力做的功为WG,弹力做的功为W弹,根据动能定理有
WG+W弹=Ek2-Ek1 (2分)
由重力做功与重力势能的关系有WG=Ep1-Ep2 (1分)
由弹力做功与弹性势能的关系有W弹=E弹1-E弹2 (1分)
联立以上三式可得Ek1+Ep1+E弹1=Ek2+Ep2+E弹2 (1分)
(2)
a.F-x图像如图所示,图中的图线和x轴围成的面积表示弹力做功的大小。 (1分)
所以弹力做功为W=-kx2 (1分)
由弹力做功与弹性势能的关系有W弹=0-E弹 (1分)
解得E弹=kx2 (1分)
b.小球由O点到P点过程中,当弹力等于重力时小球有最大速度,此时有mg=kx (1分)
根据动能定理有mgx-kx2=mv2-0 (1分)
解得v=g (1分)
18.答案 (1)38 N (2)2.1 m (3)15 m
解析 (1)由A→C过程,根据动能定理有mg[l sin θ+R(1- cos θ)]=m (2分)
根据牛顿第二定律有FN-mg= (2分)
解得FN=38 N(1分)
(2)要使物块由D点运动到E点对轨道没有压力作用,看作物块由D到E做平抛运动的逆运动,即物块运动到E点时的速度为平抛运动的初速度,运动到D点时,根据平抛运动规律有tan θ= (1分)
=2gh (1分)
解得v0=4 m/s,vy=3 m/s
则vD==5 m/s(1分)
小物块从释放点运动到D点的过程,根据动能定理有
mgd sin θ=m (2分)
解得d= m≈2.1 m(1分)
(3)从开始下滑到运动到B点的速度为零时,根据动能定理有
mgl sin θ-μmgs cos θ=0 (2分)
解得s=15 m(1分)
