中心对称复习[上学期]
图片预览


文档简介
中心对称
一、中心对称图形与两个图形成中心对称
同学们已经看到有一些图形绕某一定点(旋转中心)旋转一定角度后,可以与自身重合,如等边三角形、圆、国旗上的五角星等,这样的图形叫做旋转对称图形。如果旋转角度为180°,即若某个图形绕着中心点旋转180°后能与自身重合,我们就把这样的旋转对称图形叫做中心对称图形。这个中心点叫做对称中心。如正方形、圆、平行四边形、S形等。
把一个图形绕着某一点旋转180°,如果它能和另一个图形重合,那么我们就说这两个图形成中心对称。这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点。例如下图将△ABC绕着A点旋转180°后得到△ADE,即△ABC与△ADE是成中心对称的两个图形。点A是对称中心。点B的对称点是点D;点C的对称点是点E。点B绕着点A旋转180°到达D处,因此,B、A、D三点在同一直线上,并且AB=AD。
如果我们将这个图看成是一个图形,由于这个图形绕着点A旋转180°后,点B旋转到了点D,点C旋转到了点E,旋转后的图形恰好能与自身重合,因此也可以说这是一个中心对称图形。
二、中心对称的特征
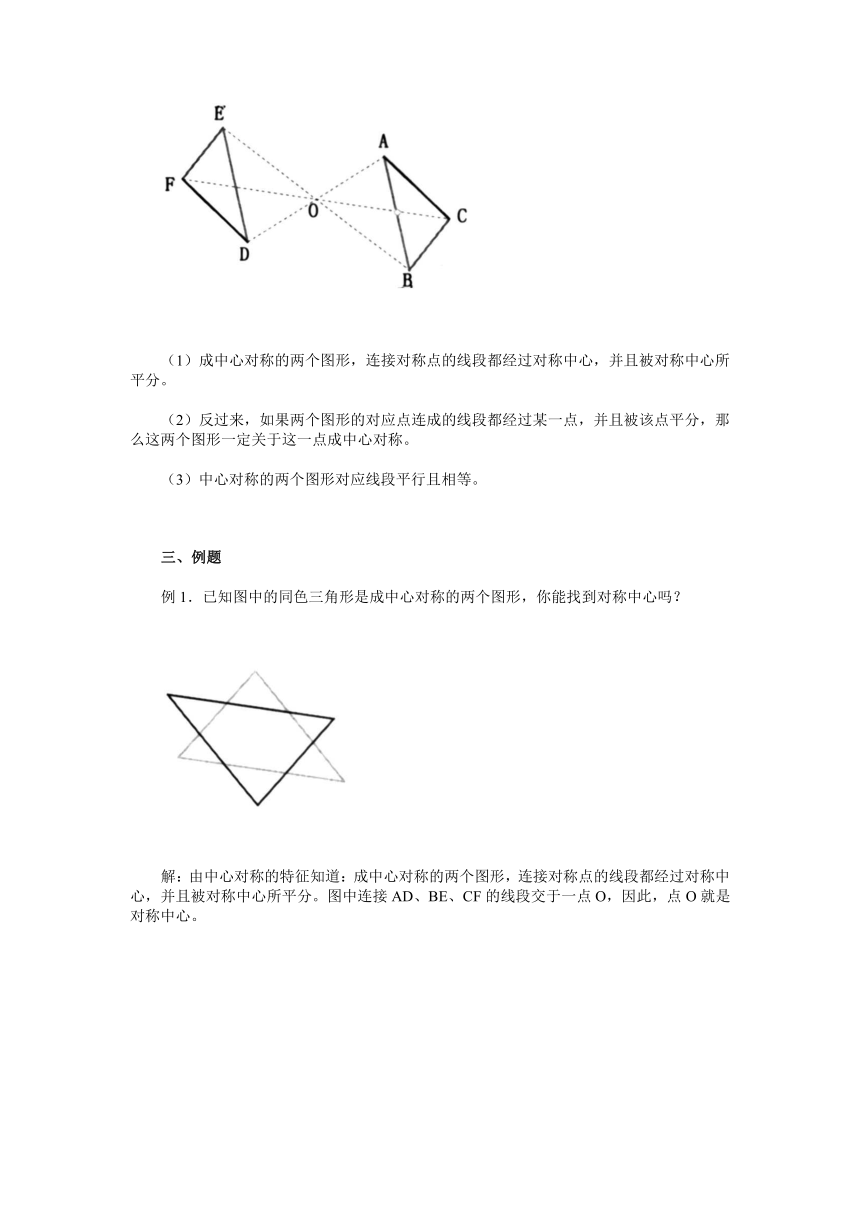
如下图,我们将△ABC绕着任意一点O点旋转180°后得到△DEF,点A绕着点O旋转180°到达D处,因此,A、O、D三点在同一直线上,并且AO=OD。
另外,点C、O、F和点B、O、E也分别在同一条直线上,并且,BO=OE,CO=OF。
成中心对称的两个图形的特征如下:
(1)成中心对称的两个图形,连接对称点的线段都经过对称中心,并且被对称中心所平分。
(2)反过来,如果两个图形的对应点连成的线段都经过某一点,并且被该点平分,那么这两个图形一定关于这一点成中心对称。
(3)中心对称的两个图形对应线段平行且相等。
三、例题
例1.已知图中的同色三角形是成中心对称的两个图形,你能找到对称中心吗?
解:由中心对称的特征知道:成中心对称的两个图形,连接对称点的线段都经过对称中心,并且被对称中心所平分。图中连接AD、BE、CF的线段交于一点O,因此,点O就是对称中心。
例2.设D为△ABC中BC边上的中点,P是AB边上的一点。Q是AC边上一点,且PD⊥DQ,求证BP+CQ>PQ
分析:要证不等关系,应该想到三角形中两边之和大于第三边。因此要想办法将CQ和BP放到同一个三角形中。
证明:由于D为△ABC中BC边上的中点,BD=DC,因此可作△DCQ关于D点的中心对称图形△DBQ1,这时,DQ=DQ1,BQ1=CQ。
又PD⊥DQ,即PD是线段QQ1的中垂线,则PQ=PQ1。在△BPQ1中,BP+BQ1>PQ1,即BP+CQ>PQ
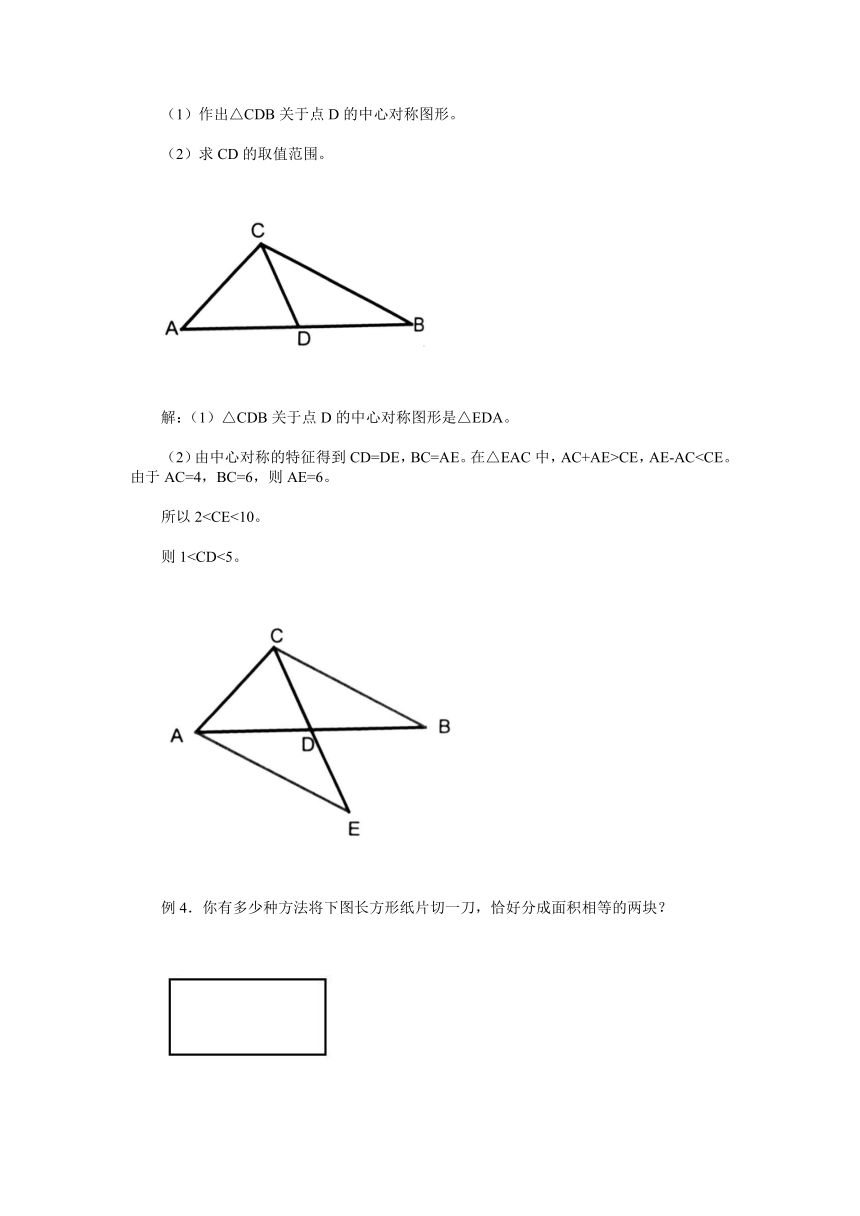
例3.△ABC中,D是AB边上的中点,AC=4,BC=6,
(1)作出△CDB关于点D的中心对称图形。
(2)求CD的取值范围。
解:(1)△CDB关于点D的中心对称图形是△EDA。
(2)由中心对称的特征得到CD=DE,BC=AE。在△EAC中,AC+AE>CE,AE-AC所以2则1
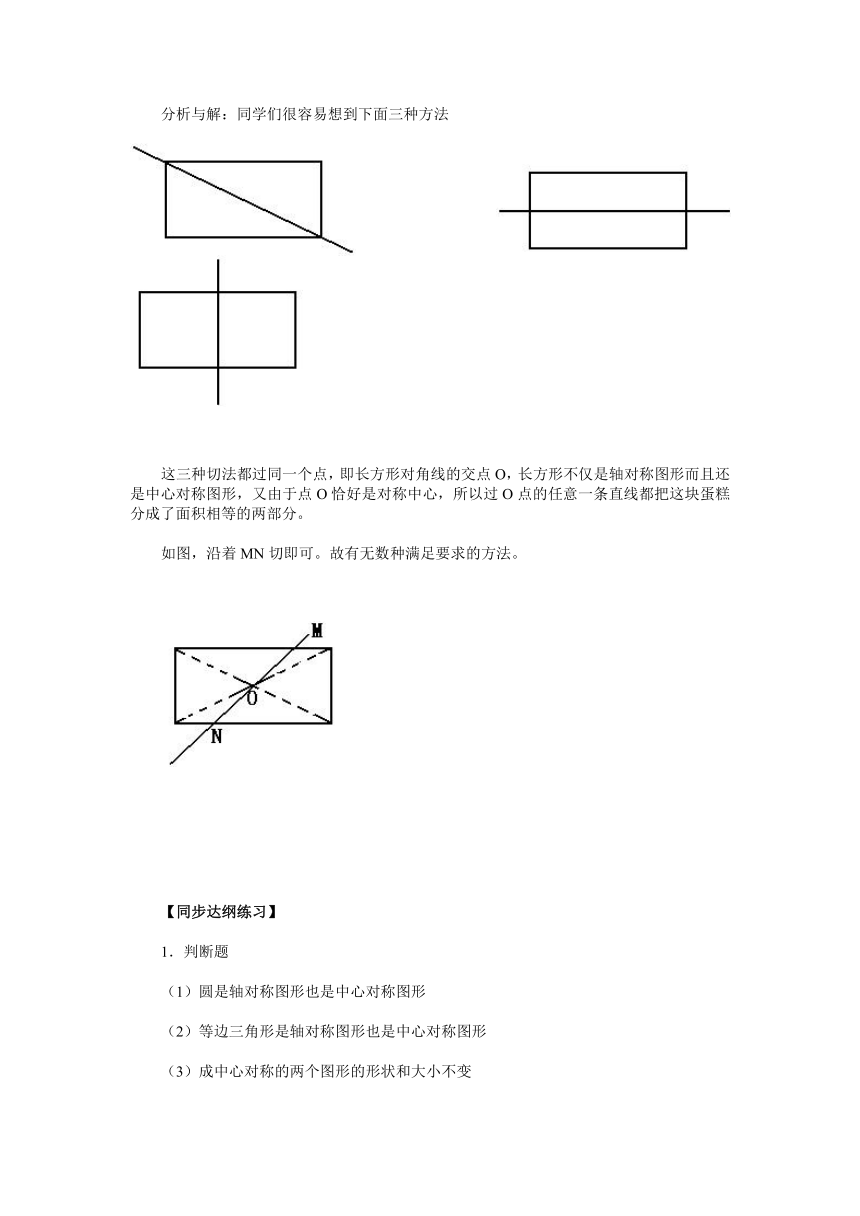
例4.你有多少种方法将下图长方形纸片切一刀,恰好分成面积相等的两块?
分析与解:同学们很容易想到下面三种方法
这三种切法都过同一个点,即长方形对角线的交点O,长方形不仅是轴对称图形而且还是中心对称图形,又由于点O恰好是对称中心,所以过O点的任意一条直线都把这块蛋糕分成了面积相等的两部分。
如图,沿着MN切即可。故有无数种满足要求的方法。
【同步达纲练习】
1.判断题
(1)圆是轴对称图形也是中心对称图形
(2)等边三角形是轴对称图形也是中心对称图形
(3)成中心对称的两个图形的形状和大小不变
(4)即是轴对称图形也是中心对称图形的四边形一定是正方形。
2.下图中的两个四边形是中心对称的,请你找出对称中心
3.画出下图关于A点的中心对称图形
4.一块方角形钢板(如图),如何用一条直线将其分为面积相等的两部分
*5.△ABC中,D是AB边上的中点,点E、F分别在AC、BC上,你能得到△ADE、△BDF面积之和与△DEF面积的大小关系吗?说说你的理由。
*6.△ABC是等腰三角形,D、E分别是腰AB及AC延长线上的点,且DG=GE。请说明BD=CE。
参考答案
【同步达纲练习】
1.(1)对 (2)错 (3)对 (4)错 例如:长方形既是轴对称图形也是中心对称图形
2.提示:两个四边形中相等的角的顶点是对称点,对称点连线的交点是对称中心
3.
4.此题分法较多,答案不唯一。
5.分析:首先利用特殊的三角形下图中的(如等边三角形)猜测结论:
。下面证明这个结论
证明:D是AB边上的中点,AD=DB,因此如下图所示可作△DAE关于D点的中心对称图形△DBM,如图连结MF,则,DE=DM,且D、E、M共线。与是等底同高的三角形,则
即
由于M、B、F三点不能在同一条直线上,则不能相等。
所以
6.
解:由于DG=GE,即D、E是关于G的对称点,作点C关于G的对称点F,连结DF,即△CEG与△FDG是中心对称的。
由中心对称的特征可知:DF//CE,DF=CE
由DF//CE,则∠ACB=∠DFB
又AB=AC,则∠ACB=∠ABC
即∠DFB=∠ABC
所以DB=DF
因此DB=CE
一、中心对称图形与两个图形成中心对称
同学们已经看到有一些图形绕某一定点(旋转中心)旋转一定角度后,可以与自身重合,如等边三角形、圆、国旗上的五角星等,这样的图形叫做旋转对称图形。如果旋转角度为180°,即若某个图形绕着中心点旋转180°后能与自身重合,我们就把这样的旋转对称图形叫做中心对称图形。这个中心点叫做对称中心。如正方形、圆、平行四边形、S形等。
把一个图形绕着某一点旋转180°,如果它能和另一个图形重合,那么我们就说这两个图形成中心对称。这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点。例如下图将△ABC绕着A点旋转180°后得到△ADE,即△ABC与△ADE是成中心对称的两个图形。点A是对称中心。点B的对称点是点D;点C的对称点是点E。点B绕着点A旋转180°到达D处,因此,B、A、D三点在同一直线上,并且AB=AD。
如果我们将这个图看成是一个图形,由于这个图形绕着点A旋转180°后,点B旋转到了点D,点C旋转到了点E,旋转后的图形恰好能与自身重合,因此也可以说这是一个中心对称图形。
二、中心对称的特征
如下图,我们将△ABC绕着任意一点O点旋转180°后得到△DEF,点A绕着点O旋转180°到达D处,因此,A、O、D三点在同一直线上,并且AO=OD。
另外,点C、O、F和点B、O、E也分别在同一条直线上,并且,BO=OE,CO=OF。
成中心对称的两个图形的特征如下:
(1)成中心对称的两个图形,连接对称点的线段都经过对称中心,并且被对称中心所平分。
(2)反过来,如果两个图形的对应点连成的线段都经过某一点,并且被该点平分,那么这两个图形一定关于这一点成中心对称。
(3)中心对称的两个图形对应线段平行且相等。
三、例题
例1.已知图中的同色三角形是成中心对称的两个图形,你能找到对称中心吗?
解:由中心对称的特征知道:成中心对称的两个图形,连接对称点的线段都经过对称中心,并且被对称中心所平分。图中连接AD、BE、CF的线段交于一点O,因此,点O就是对称中心。
例2.设D为△ABC中BC边上的中点,P是AB边上的一点。Q是AC边上一点,且PD⊥DQ,求证BP+CQ>PQ
分析:要证不等关系,应该想到三角形中两边之和大于第三边。因此要想办法将CQ和BP放到同一个三角形中。
证明:由于D为△ABC中BC边上的中点,BD=DC,因此可作△DCQ关于D点的中心对称图形△DBQ1,这时,DQ=DQ1,BQ1=CQ。
又PD⊥DQ,即PD是线段QQ1的中垂线,则PQ=PQ1。在△BPQ1中,BP+BQ1>PQ1,即BP+CQ>PQ
例3.△ABC中,D是AB边上的中点,AC=4,BC=6,
(1)作出△CDB关于点D的中心对称图形。
(2)求CD的取值范围。
解:(1)△CDB关于点D的中心对称图形是△EDA。
(2)由中心对称的特征得到CD=DE,BC=AE。在△EAC中,AC+AE>CE,AE-AC
例4.你有多少种方法将下图长方形纸片切一刀,恰好分成面积相等的两块?
分析与解:同学们很容易想到下面三种方法
这三种切法都过同一个点,即长方形对角线的交点O,长方形不仅是轴对称图形而且还是中心对称图形,又由于点O恰好是对称中心,所以过O点的任意一条直线都把这块蛋糕分成了面积相等的两部分。
如图,沿着MN切即可。故有无数种满足要求的方法。
【同步达纲练习】
1.判断题
(1)圆是轴对称图形也是中心对称图形
(2)等边三角形是轴对称图形也是中心对称图形
(3)成中心对称的两个图形的形状和大小不变
(4)即是轴对称图形也是中心对称图形的四边形一定是正方形。
2.下图中的两个四边形是中心对称的,请你找出对称中心
3.画出下图关于A点的中心对称图形
4.一块方角形钢板(如图),如何用一条直线将其分为面积相等的两部分
*5.△ABC中,D是AB边上的中点,点E、F分别在AC、BC上,你能得到△ADE、△BDF面积之和与△DEF面积的大小关系吗?说说你的理由。
*6.△ABC是等腰三角形,D、E分别是腰AB及AC延长线上的点,且DG=GE。请说明BD=CE。
参考答案
【同步达纲练习】
1.(1)对 (2)错 (3)对 (4)错 例如:长方形既是轴对称图形也是中心对称图形
2.提示:两个四边形中相等的角的顶点是对称点,对称点连线的交点是对称中心
3.
4.此题分法较多,答案不唯一。
5.分析:首先利用特殊的三角形下图中的(如等边三角形)猜测结论:
。下面证明这个结论
证明:D是AB边上的中点,AD=DB,因此如下图所示可作△DAE关于D点的中心对称图形△DBM,如图连结MF,则,DE=DM,且D、E、M共线。与是等底同高的三角形,则
即
由于M、B、F三点不能在同一条直线上,则不能相等。
所以
6.
解:由于DG=GE,即D、E是关于G的对称点,作点C关于G的对称点F,连结DF,即△CEG与△FDG是中心对称的。
由中心对称的特征可知:DF//CE,DF=CE
由DF//CE,则∠ACB=∠DFB
又AB=AC,则∠ACB=∠ABC
即∠DFB=∠ABC
所以DB=DF
因此DB=CE
