中心对称[上学期]
图片预览






文档简介
课件18张PPT。
授课人:潘 瑜
中 心 对 称重要的区别:
修定版教材把中心对称(图形)安排在平行四边形之后,而本教材正好与之相反。这样换位反映了几何教学的体系结构与教学思路有很大的改变。
本教材一个明显的特征是以中心对称为基础来研究平行四边形;而修定版的相应内容是相对独立。
这种认识同初一(下)《轴对称》与等腰三角形的教材设计、编排意图相同,所以一定要准确的领会与把握。
一、课改教材(华东版)与修定版教材的区别: 为了充分理解教材,我们有必要分析一下本章节的课标要求
1、通过具体实例认识中心对称(图形),经历观察、体验、发现、探索中心对称(图形)有关概念的提出,初步理解中心对称(图形)是特殊的旋转对称图形,旋转的角度为180°。并逐步积累审美体验
2、认识中心对称,探索它的基本性质:“连结对称点的线段都经过对称中心,并且被对称中心平分”;
“两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称”二、认识课标: 3、在观察、操作、推理、归纳等学习过程中,发展学生的合情推理能力
4、进一步培养学生的创新意识和应用能力
5、培养学生的审美意识三、难点突破:本章节难点
中心对称和中心对称图形两个概念的区别可以淡化。精力要放在通过师生互动、学生自主探索,亲历中心对称有关概念的提出及归纳总结出基本性质。
要对课本中的想一想、探索、练习、谈一谈、试一试、做一做等做到充分的把握。这才正是每个教师可以尽情发挥的阵地。
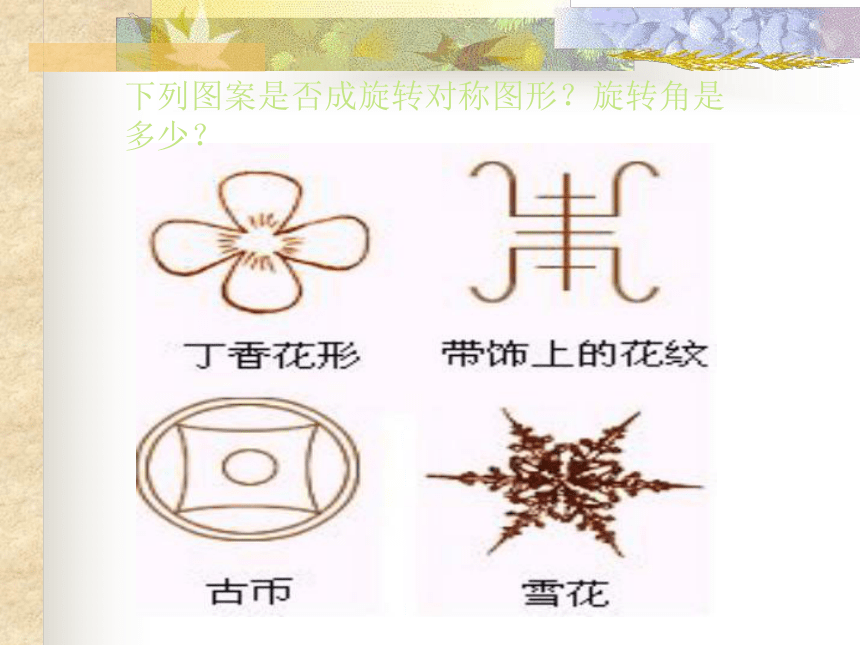
要从学生已有的轴对称知识和上一节的旋转对称图形做自然的复习或实际问题情景引入,而且要结合所教学生的学习情况收集相关素材,进行适当的补充。四、教学程序 (一)创建情景 §11.3中心对称(一) 下列图案是否成旋转对称图形?旋转角是多少?O⌒180°亲历概念的提出ABCEFGO(E)(F)(G)··································································亲历概念:已知 ABC与 EFG关于点O成中心对称,分别找出图中的对称点和对称线段。画一画:画出以下A、B、C各点关于直线 a的对称
点A’、B’、C’,连结AB、BC、CA、A’B’、B’C’、
C’A’。并想一想直线 a 两旁图形有什么关系?具有
什么性质?由此猜想中心对称(图形)有什么性质●●AaA’●●●●AaA’BB’●●● ●●●ABCaA’C’B’(1)(2)(3)大胆猜想 已知 ABC与 A’B’C’关于点O成中心对称。A’B’C’探索、验证基本性质应用:试画出以下A、B、C各点关于点O 的对称点A’、B’、C’,连结AB、BC、CA、A’B’、B’C’、C’A’,并猜一猜点O 两旁的图形成什么关系?●O●●AA’●●●●●OABA’B’●O●●●●●●ABCA’B’C’(1)(2)(3)提高
(1)已知图中的两个图形成中心对称,利用所学知识找出两图形的对称中心。 (2)你有简便方法求以下方阵中这组数据的和吗?1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
5 6 7 8 9(四)巩固与反馈练习 练习 P18~19 1、2、(五)课堂小结 1、中心对称的概念
2、中心对称的性质(六)作业设计 P21~22 1、2、3、4
选做题:
设计构成中心对称的图案,使图案比较美观,比一比,谁设计的好?
实践题:
(1) 制作一个风车
(2) 玩一玩七巧板 ,尽可能多地摆出成中心对称的图案
授课人:潘 瑜
中 心 对 称重要的区别:
修定版教材把中心对称(图形)安排在平行四边形之后,而本教材正好与之相反。这样换位反映了几何教学的体系结构与教学思路有很大的改变。
本教材一个明显的特征是以中心对称为基础来研究平行四边形;而修定版的相应内容是相对独立。
这种认识同初一(下)《轴对称》与等腰三角形的教材设计、编排意图相同,所以一定要准确的领会与把握。
一、课改教材(华东版)与修定版教材的区别: 为了充分理解教材,我们有必要分析一下本章节的课标要求
1、通过具体实例认识中心对称(图形),经历观察、体验、发现、探索中心对称(图形)有关概念的提出,初步理解中心对称(图形)是特殊的旋转对称图形,旋转的角度为180°。并逐步积累审美体验
2、认识中心对称,探索它的基本性质:“连结对称点的线段都经过对称中心,并且被对称中心平分”;
“两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称”二、认识课标: 3、在观察、操作、推理、归纳等学习过程中,发展学生的合情推理能力
4、进一步培养学生的创新意识和应用能力
5、培养学生的审美意识三、难点突破:本章节难点
中心对称和中心对称图形两个概念的区别可以淡化。精力要放在通过师生互动、学生自主探索,亲历中心对称有关概念的提出及归纳总结出基本性质。
要对课本中的想一想、探索、练习、谈一谈、试一试、做一做等做到充分的把握。这才正是每个教师可以尽情发挥的阵地。
要从学生已有的轴对称知识和上一节的旋转对称图形做自然的复习或实际问题情景引入,而且要结合所教学生的学习情况收集相关素材,进行适当的补充。四、教学程序 (一)创建情景 §11.3中心对称(一) 下列图案是否成旋转对称图形?旋转角是多少?O⌒180°亲历概念的提出ABCEFGO(E)(F)(G)··································································亲历概念:已知 ABC与 EFG关于点O成中心对称,分别找出图中的对称点和对称线段。画一画:画出以下A、B、C各点关于直线 a的对称
点A’、B’、C’,连结AB、BC、CA、A’B’、B’C’、
C’A’。并想一想直线 a 两旁图形有什么关系?具有
什么性质?由此猜想中心对称(图形)有什么性质●●AaA’●●●●AaA’BB’●●● ●●●ABCaA’C’B’(1)(2)(3)大胆猜想 已知 ABC与 A’B’C’关于点O成中心对称。A’B’C’探索、验证基本性质应用:试画出以下A、B、C各点关于点O 的对称点A’、B’、C’,连结AB、BC、CA、A’B’、B’C’、C’A’,并猜一猜点O 两旁的图形成什么关系?●O●●AA’●●●●●OABA’B’●O●●●●●●ABCA’B’C’(1)(2)(3)提高
(1)已知图中的两个图形成中心对称,利用所学知识找出两图形的对称中心。 (2)你有简便方法求以下方阵中这组数据的和吗?1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
5 6 7 8 9(四)巩固与反馈练习 练习 P18~19 1、2、(五)课堂小结 1、中心对称的概念
2、中心对称的性质(六)作业设计 P21~22 1、2、3、4
选做题:
设计构成中心对称的图案,使图案比较美观,比一比,谁设计的好?
实践题:
(1) 制作一个风车
(2) 玩一玩七巧板 ,尽可能多地摆出成中心对称的图案
