人教版三年级数学上册 第七单元第5课时解决问题表格式精品教学方案
文档属性
| 名称 | 人教版三年级数学上册 第七单元第5课时解决问题表格式精品教学方案 | 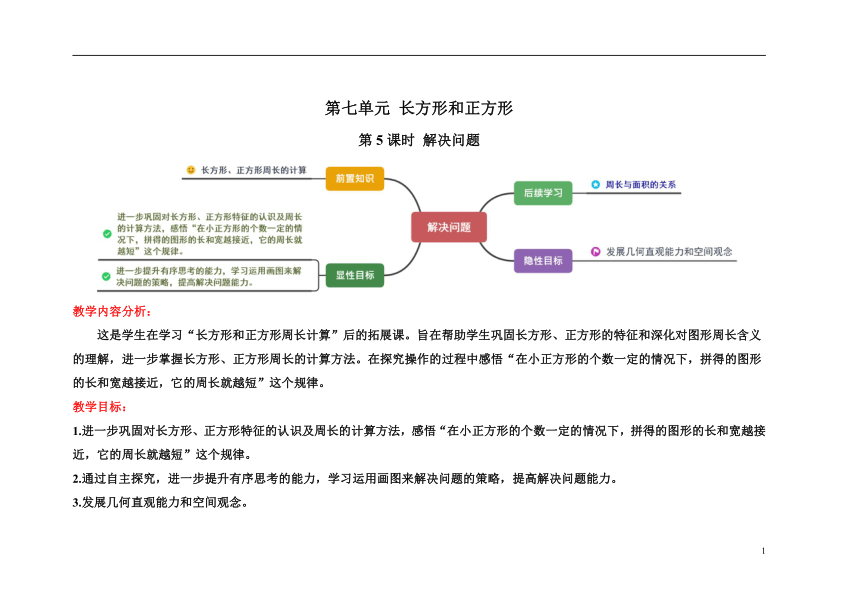 | |
| 格式 | docx | ||
| 文件大小 | 227.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-19 16:26:01 | ||
图片预览


文档简介
第七单元 长方形和正方形
第5课时 解决问题
教学内容分析:
这是学生在学习“长方形和正方形周长计算”后的拓展课。旨在帮助学生巩固长方形、正方形的特征和深化对图形周长含义的理解,进一步掌握长方形、正方形周长的计算方法。在探究操作的过程中感悟“在小正方形的个数一定的情况下,拼得的图形的长和宽越接近,它的周长就越短”这个规律。
教学目标:
1.进一步巩固对长方形、正方形特征的认识及周长的计算方法,感悟“在小正方形的个数一定的情况下,拼得的图形的长和宽越接近,它的周长就越短”这个规律。
2.通过自主探究,进一步提升有序思考的能力,学习运用画图来解决问题的策略,提高解决问题能力。
3.发展几何直观能力和空间观念。
教学重点:进一步巩固对长方形、正方形特征的认识及周长的计算方法,感悟“在小正方形的个数一定的情况下,拼得的图形的长和宽越接近,它的周长就越短”这个规律。
教学难点:用有序思考的方法解决问题。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 用4个边长为1分米的小正方体拼成长方形和正方形,周长分别是多少? 小结:长方形、正方形的周长是指外面一圈的长度。 学生独立画图计算并回答: ①拼成一个长4分米、宽1分米的长方形,周长是10分米。(4+1)×2=10(分米) ②拼成一个边长为2分米的正方形,周长是8分米。2×4=8(分米) 明确长方形、正方形的周长是指外面一圈的长度,巩固长方形、正方形周长的计算方法,为接下来的探究奠定基础。
环节二 探究新知 1.呈现问题:用16张边长是1分米的正方形纸拼成长方形和正方形。怎样拼,才能使拼成的图形周长最短? 2.引导阅读与理解:你找到了哪些数学信息?这里要解决什么问题 3.组织自主探索 要求:在方格纸上画一画,算一算周长,比较哪种拼法周长最短。 4.组织反馈 5.引导比较:对比这几个图形的周长,哪个图形的周长最短? 5. 回顾反思:现在我们将所有拼法都罗列出来了吗?你怎么想的? 小结:根据图形的特点,有序思考。通过对比,可以找到周长最短的图形。 阅读并回答: ①用16张正方形纸拼图形,要使拼成的图形是长方形或者正方形。 ②小正方形的边长是1分米。 ③这里有不同的拼法。 ④要解决的问题是哪种拼法周长最短。 自主尝试 学生回答: ①拼成一个长16分米、宽1分米的长方形,周长是34分米。(16+1)×2=34(分米) ②拼成一个边长为4分米的正方形,周长是16分米。4×4=16(分米) ③拼成一个长8分米,宽2分米的长方形,周长是20分米。(8+2)×2=20(分米) 学生回答 16分米<20分米<34分米 拼成正方形周长最短。 学生思考后,同桌交流,回答问题。 根据长方形、正方形的特点思考,长方形对边相等,正方形四边相等。 我们有序思考,将16个小正方形拼成一行,就是长为16分米,宽1分米的长方形。 拼成两行,就是长为8分米,宽2分米的长方形。16个小正方形不能正好拼成3行。 拼成4行,就是边长为4分米的正方形。拼成5行、6行、7行都不行。 拼成8行的话,与前面长8分米、宽2分米的长方形重复了。所以只有这样三种拼法。 引导阅读与理解,明确数学信息和要解决的问题。 引导在方格纸上画一画解决问题,借助画图思考问题、解决问题。 尊重学生的想法,充分反馈学生的思路。 通过“现在我们将所有拼法都罗列出来了吗?”引导学生反思解决问题的过程,用有序思考的方法解决问题。
环节三 巩固练习 (一)进一步探究 1.呈现问题:用36张边长是1分米的正方形纸拼成长方形和正方形。怎样拼,才能使拼成的图形周长最短? 2.提示:在方格纸上画一画、写一写、算一算。 3.对比:这几个图形的周长,哪个图形的周长最短?你有什么发现? 3.小结:同学们能够根据长方形、正方形的特征,有序思考。利用画图,帮助找全所有拼法。 (二)探究原理 1.提出疑问。通过刚才两个问题的解决,我们发现,当小正方形的个数相同时,长方形、正方形长和宽越接近,周长越短。对于这个发现,你有什么疑问吗? 2.组织讨论 3.小结 边重叠得越多,拼成的图形周长就越短。 独立尝试后回答: 我们有序思考,将36个小正方形拼成一行,就是长36分米,宽1分米的长方形,周长是74分米。 拼成两行,就是长为18分米,宽2分米的长方形,周长是40分米。 拼成三行,就是长为12分米,宽3分米的长方形,周长是30分米。 拼成四行,就是长为9分米,宽4分米的长方形,周长是26分米。 拼成六行,就是边长为6分米的正方形,周长是24分米。 学生回答: ①24<26<30<40<74,正方形的周长最短。 ②我发现,小正方形的个数相同,长方形、正方形长和宽越接近,周长越短。 学生回答: 为什么小正方形的个数相同,长方形、正方形长和宽越接近,周长越短呢? 自主探究,小组讨论 学生回答: 以16个小正方形为例。 16个小正方形分开摆放时,一共有64条边。 排成一行时,因为两个正方形拼在一起就少了2条边,一共少了15×2条边,周长是64-30=34(分米)。 排成两行时,因为左右两个正方形拼在一起少了2条边,上下两个正方形拼在一起又少了2条边,一共少了22×2条边,周长是64-44=20(分米)。 排成4行时,因为左右两个正方形拼在一起少了2条边,上下两个正方形拼在一起又少了2条边,一共少了24×2条边,周长是64-48=16(分米)。 运用有序思考的方法解决问题,进一步探究规律。 引导提出问题,指向周长规律背后的奥秘。 以16个小正方形为例,采用数形结合的方式理解“边重叠得越多,拼成的图形周长就越短。”
环节四 课堂小结 小结:边重叠得越多,拼成的图形周长就越短。所以当小正方形个数相同时,长和宽越接近,周长越短。 总结规律,利于迁移运用。
环节五 拓展延伸 把 12 盒这样的保鲜膜捆在一起,怎样捆最节省胶带? 自主尝试并回答 这一题相当于是问“12个边长5厘米的正方形怎样拼周长最短”。根据我们之前发现的规律,长方形的长和宽越接近,周长越短。这里长和宽最接近的是拼成长20厘米,宽15厘米的长方形,周长是70厘米,所以这里从中间捆最节省胶带,胶带长度是70厘米。 引导学生将“12盒保鲜膜捆胶带怎样最省”的实际问题转化为“将12个边长5厘米的正方形拼组后的图形周长最短”的数学问题。运用规律解决问题,提升将生活中实际问题转化为数学问题的能力。
环节六 布置作业 教材P87第4题。
1
第5课时 解决问题
教学内容分析:
这是学生在学习“长方形和正方形周长计算”后的拓展课。旨在帮助学生巩固长方形、正方形的特征和深化对图形周长含义的理解,进一步掌握长方形、正方形周长的计算方法。在探究操作的过程中感悟“在小正方形的个数一定的情况下,拼得的图形的长和宽越接近,它的周长就越短”这个规律。
教学目标:
1.进一步巩固对长方形、正方形特征的认识及周长的计算方法,感悟“在小正方形的个数一定的情况下,拼得的图形的长和宽越接近,它的周长就越短”这个规律。
2.通过自主探究,进一步提升有序思考的能力,学习运用画图来解决问题的策略,提高解决问题能力。
3.发展几何直观能力和空间观念。
教学重点:进一步巩固对长方形、正方形特征的认识及周长的计算方法,感悟“在小正方形的个数一定的情况下,拼得的图形的长和宽越接近,它的周长就越短”这个规律。
教学难点:用有序思考的方法解决问题。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 用4个边长为1分米的小正方体拼成长方形和正方形,周长分别是多少? 小结:长方形、正方形的周长是指外面一圈的长度。 学生独立画图计算并回答: ①拼成一个长4分米、宽1分米的长方形,周长是10分米。(4+1)×2=10(分米) ②拼成一个边长为2分米的正方形,周长是8分米。2×4=8(分米) 明确长方形、正方形的周长是指外面一圈的长度,巩固长方形、正方形周长的计算方法,为接下来的探究奠定基础。
环节二 探究新知 1.呈现问题:用16张边长是1分米的正方形纸拼成长方形和正方形。怎样拼,才能使拼成的图形周长最短? 2.引导阅读与理解:你找到了哪些数学信息?这里要解决什么问题 3.组织自主探索 要求:在方格纸上画一画,算一算周长,比较哪种拼法周长最短。 4.组织反馈 5.引导比较:对比这几个图形的周长,哪个图形的周长最短? 5. 回顾反思:现在我们将所有拼法都罗列出来了吗?你怎么想的? 小结:根据图形的特点,有序思考。通过对比,可以找到周长最短的图形。 阅读并回答: ①用16张正方形纸拼图形,要使拼成的图形是长方形或者正方形。 ②小正方形的边长是1分米。 ③这里有不同的拼法。 ④要解决的问题是哪种拼法周长最短。 自主尝试 学生回答: ①拼成一个长16分米、宽1分米的长方形,周长是34分米。(16+1)×2=34(分米) ②拼成一个边长为4分米的正方形,周长是16分米。4×4=16(分米) ③拼成一个长8分米,宽2分米的长方形,周长是20分米。(8+2)×2=20(分米) 学生回答 16分米<20分米<34分米 拼成正方形周长最短。 学生思考后,同桌交流,回答问题。 根据长方形、正方形的特点思考,长方形对边相等,正方形四边相等。 我们有序思考,将16个小正方形拼成一行,就是长为16分米,宽1分米的长方形。 拼成两行,就是长为8分米,宽2分米的长方形。16个小正方形不能正好拼成3行。 拼成4行,就是边长为4分米的正方形。拼成5行、6行、7行都不行。 拼成8行的话,与前面长8分米、宽2分米的长方形重复了。所以只有这样三种拼法。 引导阅读与理解,明确数学信息和要解决的问题。 引导在方格纸上画一画解决问题,借助画图思考问题、解决问题。 尊重学生的想法,充分反馈学生的思路。 通过“现在我们将所有拼法都罗列出来了吗?”引导学生反思解决问题的过程,用有序思考的方法解决问题。
环节三 巩固练习 (一)进一步探究 1.呈现问题:用36张边长是1分米的正方形纸拼成长方形和正方形。怎样拼,才能使拼成的图形周长最短? 2.提示:在方格纸上画一画、写一写、算一算。 3.对比:这几个图形的周长,哪个图形的周长最短?你有什么发现? 3.小结:同学们能够根据长方形、正方形的特征,有序思考。利用画图,帮助找全所有拼法。 (二)探究原理 1.提出疑问。通过刚才两个问题的解决,我们发现,当小正方形的个数相同时,长方形、正方形长和宽越接近,周长越短。对于这个发现,你有什么疑问吗? 2.组织讨论 3.小结 边重叠得越多,拼成的图形周长就越短。 独立尝试后回答: 我们有序思考,将36个小正方形拼成一行,就是长36分米,宽1分米的长方形,周长是74分米。 拼成两行,就是长为18分米,宽2分米的长方形,周长是40分米。 拼成三行,就是长为12分米,宽3分米的长方形,周长是30分米。 拼成四行,就是长为9分米,宽4分米的长方形,周长是26分米。 拼成六行,就是边长为6分米的正方形,周长是24分米。 学生回答: ①24<26<30<40<74,正方形的周长最短。 ②我发现,小正方形的个数相同,长方形、正方形长和宽越接近,周长越短。 学生回答: 为什么小正方形的个数相同,长方形、正方形长和宽越接近,周长越短呢? 自主探究,小组讨论 学生回答: 以16个小正方形为例。 16个小正方形分开摆放时,一共有64条边。 排成一行时,因为两个正方形拼在一起就少了2条边,一共少了15×2条边,周长是64-30=34(分米)。 排成两行时,因为左右两个正方形拼在一起少了2条边,上下两个正方形拼在一起又少了2条边,一共少了22×2条边,周长是64-44=20(分米)。 排成4行时,因为左右两个正方形拼在一起少了2条边,上下两个正方形拼在一起又少了2条边,一共少了24×2条边,周长是64-48=16(分米)。 运用有序思考的方法解决问题,进一步探究规律。 引导提出问题,指向周长规律背后的奥秘。 以16个小正方形为例,采用数形结合的方式理解“边重叠得越多,拼成的图形周长就越短。”
环节四 课堂小结 小结:边重叠得越多,拼成的图形周长就越短。所以当小正方形个数相同时,长和宽越接近,周长越短。 总结规律,利于迁移运用。
环节五 拓展延伸 把 12 盒这样的保鲜膜捆在一起,怎样捆最节省胶带? 自主尝试并回答 这一题相当于是问“12个边长5厘米的正方形怎样拼周长最短”。根据我们之前发现的规律,长方形的长和宽越接近,周长越短。这里长和宽最接近的是拼成长20厘米,宽15厘米的长方形,周长是70厘米,所以这里从中间捆最节省胶带,胶带长度是70厘米。 引导学生将“12盒保鲜膜捆胶带怎样最省”的实际问题转化为“将12个边长5厘米的正方形拼组后的图形周长最短”的数学问题。运用规律解决问题,提升将生活中实际问题转化为数学问题的能力。
环节六 布置作业 教材P87第4题。
1
