第六单元运算律易错点测试卷(单元测试) 小学数学四年级下册苏教版(含答案)
文档属性
| 名称 | 第六单元运算律易错点测试卷(单元测试) 小学数学四年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 22:21:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第六单元运算律易错点测试卷(单元测试)-小学数学四年级下册苏教版
一、选择题
1.根据下图计算小明和小芳两家相距的米数,有名同学列出了两个算式:(70+60)×4,70×4+60×4,他的两种解法实际上运用了( )。
A.加法结合律 B.乘法结合律 C.乘法分配律
2.小林和红红在学校操场的环形跑道上跑步,他们同时从同一起点出发向相反的方向跑。红红每秒跑3米,小林每秒跑5米,45秒后他们第一次相遇,操场跑道长( )米。
A.225 B.360 C.90
3.99×99+99与100×100相比,前者( )后者。
A.大于 B.小于 C.等于
4.小秦要打一篇1200字的稿件,已经打了5分钟,平均每分钟打80字,剩余的平均每分钟打100字,还要打( )分钟才能打完。
A.12 B.7 C.8
5.与a×9-b×9相等的式子是( )。
A.(a+b)×9 B.(a-b)×(9+9) C.(a-b)×9
6.78×49+78×51=( )。
A.(78×78)×(49×51) B.78×(49+51) C.78×49×51
二、填空题
7.在括号里填上“>”“<”或“=”。
260×14( )260×10+4 320×4×5( )320×20
80÷(4×5)( )80÷4×5 580×47( )470×58
8.★+●+▲=●+(★+▲),运用了( )(填运算律)。
9.小明在计算12×(★+20)时,算成了12×★+20,这样算出来的得数比原来少了( )。
10.根据运算律在横线上填上合适的数。
(1)260+(140+90)=(260+_____)+_____
(2)_____×46=_____×58
(3)125×27×8=27×(_____×_____)
(4)68×_____+32×_____=(_____+_____)×36
11.要使125×32计算起来较为简便,可将32变成( )×( ),将原式变成( )。
12.观察下面的前三道题,在括号里填合适的数。
25×8=25×4×2=200
25×12=25×4×3=300
25×16=25×4×4=400
25×20=25×( )×( )=( )
25×28=25×( )×( )=( )
25×36=25×( )×( )=( )
13.下图竖式,箭头部分算的是( )×( ),乘法笔算的过程应用了哪一个运算律?( )。
14.在计算370÷5÷2、9998×346×0×12456、456×37时,你认为哪道算式用计算器计算最合适,请写在括号里。( )
三、判断题
15.458-99=458-100-1。( )
16.125÷(25×5)=125÷25×5=1。( )
17.欧洲人用“双倍法”计算46×13,是用46的8倍+4倍+1倍。( )
18.因为△+□=〇,●×〇=◎,所以△×●+□×●=◎。( )
19.将算式14×28×25改成28×(14×25),只运用了乘法结合律。( )
四、计算题
20.直接写得数。
21.计算下面各题。(带☆的题要用简便方法计算)
400÷16×5 528-28×11 ☆720÷16÷5
800÷[(197-189)×5] 912-874÷(28+10) ☆36×25
五、解答题
22.刘师傅和张师傅共同加工一批零件,24天正好加工完。刘师傅每天加工82个零件,张师傅每天加工79个零件。这批零件一共有多少个?
23.小军和小琴两人同时从相距2千米的两地相向而行。小军每分钟行120米,小琴每分钟行80米。如果一只狗与小军同时出发,同向而行。当它遇到小琴后,立即回头向小军跑去。这样来回不断,直到小军和小琴相遇为止,这时狗一共跑了4千米。这只狗每分钟行多少米?
24.王老师和张老师同时从家出发去科技馆(如图),王老师步行速度是85米/分,张老师骑行速度是215米/分,12分钟后两人同时到达。沿图中的路线,从王老师家到张老师家的路程是多少米?
25.疫情期间,社区服务人员义务为居民采购蔬菜,购进8筐西红柿和8筐黄瓜,每筐西红柿68千克,每筐黄瓜57千克。请你算一算,购进西红柿和黄瓜一共多少千克?
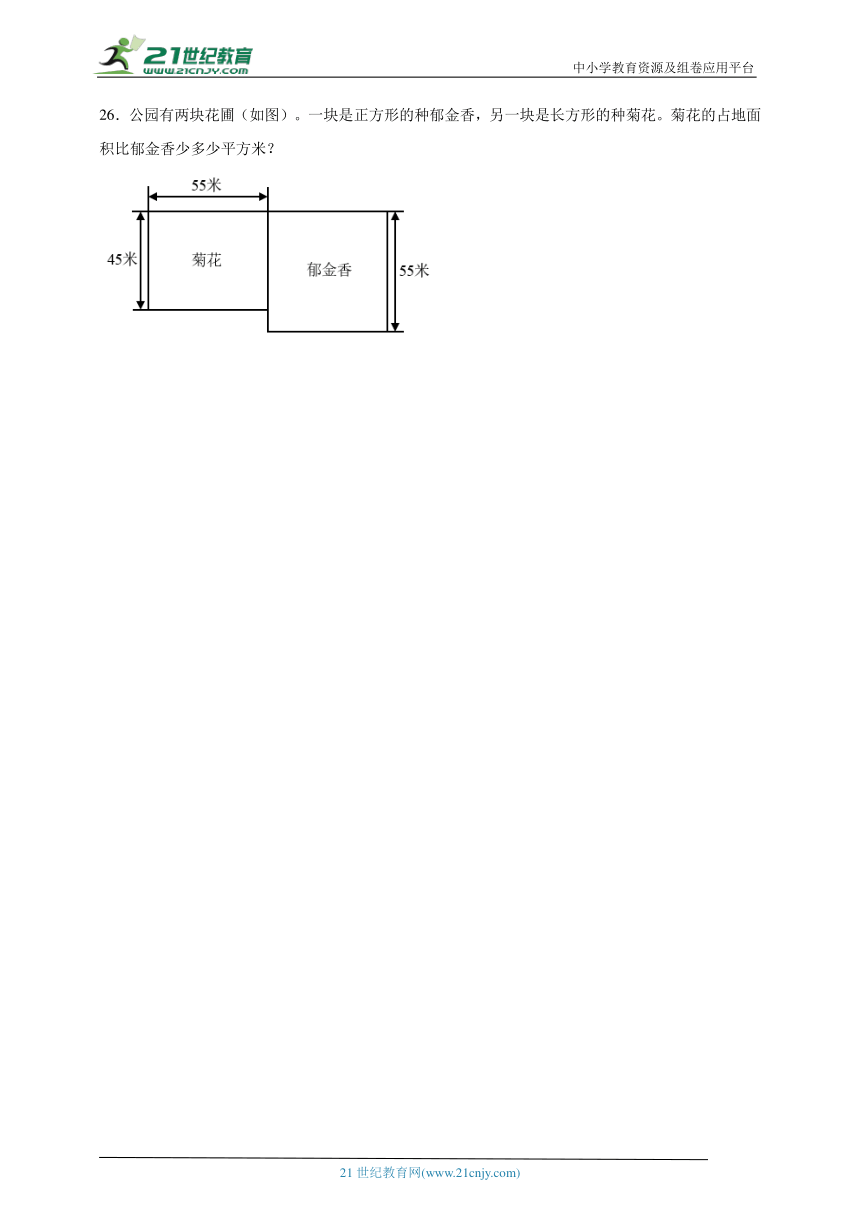
26.公园有两块花圃(如图)。一块是正方形的种郁金香,另一块是长方形的种菊花。菊花的占地面积比郁金香少多少平方米?
参考答案:
1.C
【分析】乘法分配律是指两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变。据此可知,计算70×4+60×4时,先提相同的因数4,再将剩下部分相加,用这个和乘4,进行简算。则70×4+60×4=(70+60)×4运用了乘法分配律。
【详解】70×4+60×4
=(70+60)×4
=130×4
=520(千米)
他的两种解法实际上运用了乘法分配律。
故答案为:C
【点睛】本题考查学生对乘法分配律的应用和掌握情况。
2.B
【分析】他们从同一起点向相反方向跑封闭的环形跑道,第一次相遇时两人跑的路程就是跑道的长度,所以两人跑的速度和乘相遇的时间就是跑道的长度。
【详解】(3+5)×45
=8×45
=360(米)
操场跑道长360米。
故答案为:B
【点睛】本题考查简单的相遇行程应用题,主要运用行程问题的数量关系来解答。
3.B
【分析】根据乘法分配律计算99×99+99时,先提取公因数99,再将剩下部分相加。用99乘这个和进行简算。则99×99+99=99×100。再比较99×100与100×100的大小即可。
【详解】99×99+99
=99×(99+1)
=99×100
99<100
则99×100<100×100
也就是99×99+99<100×100。
故答案为:B
【点睛】本题关键是熟练掌握乘法分配律,将算式99×99+99变换为99×100。
4.C
【分析】80乘5等于5分钟打字个数,1200减5分钟打字个数等于剩余没打的字数,再除以100即等于还要打字的分钟数。
【详解】(1200-80×5)÷100
=800÷100
=8(分钟)
还要打8分钟才能打完。
故答案为:C
【点睛】本题的关键是读懂题意,理清题中的数量关系,再确定先算什么,最后再算什么。
5.C
【分析】乘法分配律:两个数的差与第三个数相乘,可以把被减数和减数分别同第三个数相乘,再把两个积相减,结果不变;乘法分配律也可以逆运用。
【详解】根据分析可得:a×9-b×9=(a-b)×9。
故答案为:C
【点睛】本题考查的是乘法分配律的灵活运用。
6.B
【分析】乘法分配律:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加;乘法分配律也可以逆运用。
【详解】根据分析可得:78×49+78×51=78×(49+51)。
故答案为:B
【点睛】熟练掌握乘法分配律的定义是解答此题的关键。
7. > = < =
【分析】(1)260×14表示14个260的和,260×10+4表示10个260的和再加上1个4,14个260的和一定大于10个260的和再加上1个4;
(2)一个数连续乘两个数,等于这个数乘后两个数的积;
(3)80÷(4×5)=80÷4÷5,一个数(0除外)除以5的商一定小于这个数乘5的积;
(4)580×47的积等于58×47的积的末尾再加上1个0,470×58的积等于47×58的积的末尾再加上1个0。
【详解】(1)260×14>260×10+4;
(2)320×4×5=320×20;
(3)80÷(4×5)=80÷4÷5,80÷4÷5<80÷4×5,则80÷(4×5)<80÷4×5;
(4)580×47=470×58。
【点睛】算式的大小比较通常是口算或估算出结果再根据结果进行比较,或先找规律或性质,然后再根据规律或性质进行比较。
8.加法交换律和加法结合律
【分析】加法交换率是两个加数交换位置,和不变,公式a+b=b+a;
加法结合率是三个数相加,先把前两个数相加或先把后两个数相加,再加第三个数,和不变,公式a+b+c=(a+b)+c=a+(b+c);
据此判断即可。
【详解】根据题干,★和●两个加数的位置进行了交换,根据加法交换律的意义可知,★+●+▲=●+(★+▲),运用了加法交换律;
算式中加了括号,先把后两个数相加,所以还运用了加法结合律。
【点睛】本题考查了加法交换律和加法结合律的意义。
9.220
【分析】计算12×(★+20)时,运用乘法分配律进行解答,再减去(12×★+20),即可解答。
【详解】12×(★+20)-(12×★+20)
=12×★+20×12-12×★-20
=240-20
=220
这样算出来的得数比原来少了220。
【点睛】此题考查了灵活运用乘法分配律进行简算。
10.(1) 140 90
(2) 58 46
(3) 125 8
(4) 36 36 68 32
【分析】(1)加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。据此解答
(2)乘法交换律:两个数相乘,交换因数的位置,积不变。据此解答
(3)乘法结合律:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。据此解答
(4)乘法分配律是指两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。据此解答
(1)
260+(140+90)=(260+140)+90
(2)
58×46=46×58
(3)
125×27×8=27×(125×8)
(4)
68×36+32×36=(68+32)×36
【点睛】本题解题关键是要熟练掌握运算律并灵活运用。
11. 8 4 125×8×4
【分析】乘法结合律:三个数相乘,先把前两个数相乘或先把后两个数相乘,积不变。据此解答。
【详解】125×32
=125×8×4
=1000×4
=4000
所以计算125×32,可将32变成8×4,将原式变成125×8×4。
【点睛】本题解题关键是要熟练掌握乘法结合律的特点。
12. 4 5 500 4 7 700 4 9 900
【分析】乘法结合律:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。用字母表示为:a×b×c=a×(b×c)。观察前三个式子发现,第二个因数都分成4与一个数的积。据此解答。
【详解】25×20=25×4×5=500;
25×28=25×4×7=700;
25×36=25×4×9=900。
【点睛】解答此题的关键是熟练掌握乘法结合律并且仔细观察式子特点,然后找出规律,根据规律填出同类算式的结果。
13. 145 10 乘法分配律
【分析】观察竖式可知,箭头部分是145与12的十位上1的乘积,即145×10,表示1450,290是145与2的乘积,然后把它们相加即等于145×12的积,所以乘法笔算的过程应用了乘法分配律;据此即可解答。
【详解】根据分析可知,竖式中,箭头部分算的是145×10,乘法笔算的过程应用了乘法分配律。
【点睛】本题主要考查了学生对整数乘法和乘法分配律的掌握及灵活运用。
14.456×37
【分析】由题意可得, 370÷5÷2用除法的性质先计算5×2=10,再计算370÷10=37;9998×346×0×12456中乘数有0,则结果直接为0;456×37需要用计算器进行计算。
【详解】在计算370÷5÷2、9998×346×0×12456、456×37时,456×37用计算器计算最合适。
【点睛】此题考查了乘除法的应用,关键是先看各算式是否能用简便算法计算。
15.×
【分析】458-99,因为99接近整百,可以把它先看做100,就是458-100,因为100比99多1,这样一来就多减去了1,再在式子的后面把多减去的加回来,就是458-100+1。
【详解】根据分析可知:
458-99=458-100+1,原题错误。
故答案为:×
【点睛】简便算法变化多端,要理解算理,要熟悉数字之间存在的关系,再运用简便算法。
16.×
【分析】除法性质:一个数连续除以两个数,可以先把后两个数相乘,再相除。如a÷b÷c=a÷(b×c);据此解答即可。
【详解】125÷(25×5)
=125÷25÷5
=5÷5
=1
125÷(25×5)≠125÷25×5,所以原题计算错误。
故答案为:×
【点睛】本题考查了学生对于整数除法性质的理解及运用。
17.√
【分析】把13分解为8、4、1的和,再分别计算出46的8倍,46的4倍,46的1倍,最后将所得积相加即可。
【详解】46×13
=46×(8+4+1)
=46×8+46×4+46×1
故答案为:√
【点睛】一个数的几倍,即用这个数乘几。
18.√
【分析】利用等量代换,把等式△+□=〇代入到算式●×〇中去,利用乘法分配律计算后判断即可。
【详解】将等式△+□=〇代入算式●×〇,得:
●×〇=●×(△+□)
=△×●+□×●
=◎
所以原题的说法正确。
故答案为:√
【点睛】本题是一道简单的等量代换问题,“〇”的代换是解决本题的关键。
19.×
【分析】乘法结合律为:在乘法算式中,先将前两个数相乘,或先将后两个数相乘,积不变;乘法交换律是交换因数的位置,积不变;算式14×28×25=28×(14×25)首先运用了乘法交换律,然后运用了乘法结合律。
【详解】由分析得:
将算式14×28×25改成28×(14×25),运用了乘法交换律和乘法结合律。
故答案为:×
【点睛】我们要牢记乘法交换律、乘法结合律的概念,根据概念灵活运用,同时要注意简便算法经常综合在一起使用。
20.7;80;5;36;130
21;101;2000;110;0
【解析】略
21.125;220;9
20;889;900
【分析】400÷16×5按照从左到右的顺序计算;
528-28×11先算乘法再算减法;
720÷16÷5运用除法的性质简便计算;
800÷[(197-189)×5] 先算小括号里减法,再算中括号里乘法,最后算除法;
912-874÷(28+10)先算小括号里加法,再算除法,最后算减法;
36×25,把36换成9×4,即原式变为:9×4×25,运用乘法结合律简便计算。
【详解】400÷16×5
=25×5
=125
528-28×11
=528-308
=220
720÷16÷5
=720÷(16×5)
=720÷80
=9
800÷[(197-189)×5]
=800÷[8×5]
=800÷40
=20
912-874÷(28+10)
=912-874÷38
=912-23
=889
36×25
=9×4×25
=9×(4×25)
=9×100
=900
22.3864个
【分析】用刘师傅平均每天加工零件个数加上张师傅平均每天加工零件个数,求出两人平均每天加工零件总个数。再乘加工天数,即可求出这批零件总个数。
【详解】(82+79)×24
=161×24
=3864(个)
答:这批零件一共有3864个。
【点睛】本题先求出两人平均每天加工零件总个数,再根据工作总量=工作效率×工作时间解答。
23.400米
【分析】由于无论狗在两人之间跑了多少个来回,狗所走的时间与小军、小琴两人相遇所用的时间是一样的,问题转化为求小军、小琴两人相遇所用的时间,也就是狗行走的时间;再根据路程÷时间=速度,这只狗每分钟行多少米,即可解答题目。
【详解】2千米=2000米
2000÷(120+80)
=2000÷200
=10(分钟)
4千米=4000米
4000÷10=400(米)
答:这只狗每分钟行400米。
【点睛】本题属于相遇问题,要求小狗跑的速度,已知小狗跑的路程,关键是得到小狗跑的时间,然后用关系式:路程÷时间=速度进行解答。
24.3600米
【详解】根据速度×时间=路程,用王老师、张老师的速度之和乘两人同时到达科技馆用的时间,即可求出从王老师家到张老师家的路程是多少米。
【解答】(85+215)×12
=300×12
=3600(米)
答:从王老师家到张老师家的路程是3600米。
【点睛】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
25.1000千克
【分析】用68乘8,求出8筐西红柿的质量;用57乘8,求出8筐黄瓜的质量;再用8筐西红柿的质量加上8筐黄瓜的质量,即68×8+57×8,此算式可以根据乘法分配律进行简算,则改写成(68+57)×8,据此解答。
【详解】68×8+57×8
=(68+57)×8
=125×8
=1000(千克)
答:购进西红柿和黄瓜一共1000千克。
【点睛】本题考查了学生对乘法分配律的掌握与运用。
26.550平方米
【分析】正方形的边长是55米,55乘55即可求出正方形面积,长方形菊花地的长是55米,宽是45米,55乘45即可求出菊花地的面积,再用郁金香地的面积减菊花地的面积即可解答。
【详解】55×55-55×45
=55×(55-45)
=55×10
=550(平方米)
答:菊花的占地面积比郁金香少550平方米。
【点睛】正方形面积=边长×边长,长方形面积=长×宽。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六单元运算律易错点测试卷(单元测试)-小学数学四年级下册苏教版
一、选择题
1.根据下图计算小明和小芳两家相距的米数,有名同学列出了两个算式:(70+60)×4,70×4+60×4,他的两种解法实际上运用了( )。
A.加法结合律 B.乘法结合律 C.乘法分配律
2.小林和红红在学校操场的环形跑道上跑步,他们同时从同一起点出发向相反的方向跑。红红每秒跑3米,小林每秒跑5米,45秒后他们第一次相遇,操场跑道长( )米。
A.225 B.360 C.90
3.99×99+99与100×100相比,前者( )后者。
A.大于 B.小于 C.等于
4.小秦要打一篇1200字的稿件,已经打了5分钟,平均每分钟打80字,剩余的平均每分钟打100字,还要打( )分钟才能打完。
A.12 B.7 C.8
5.与a×9-b×9相等的式子是( )。
A.(a+b)×9 B.(a-b)×(9+9) C.(a-b)×9
6.78×49+78×51=( )。
A.(78×78)×(49×51) B.78×(49+51) C.78×49×51
二、填空题
7.在括号里填上“>”“<”或“=”。
260×14( )260×10+4 320×4×5( )320×20
80÷(4×5)( )80÷4×5 580×47( )470×58
8.★+●+▲=●+(★+▲),运用了( )(填运算律)。
9.小明在计算12×(★+20)时,算成了12×★+20,这样算出来的得数比原来少了( )。
10.根据运算律在横线上填上合适的数。
(1)260+(140+90)=(260+_____)+_____
(2)_____×46=_____×58
(3)125×27×8=27×(_____×_____)
(4)68×_____+32×_____=(_____+_____)×36
11.要使125×32计算起来较为简便,可将32变成( )×( ),将原式变成( )。
12.观察下面的前三道题,在括号里填合适的数。
25×8=25×4×2=200
25×12=25×4×3=300
25×16=25×4×4=400
25×20=25×( )×( )=( )
25×28=25×( )×( )=( )
25×36=25×( )×( )=( )
13.下图竖式,箭头部分算的是( )×( ),乘法笔算的过程应用了哪一个运算律?( )。
14.在计算370÷5÷2、9998×346×0×12456、456×37时,你认为哪道算式用计算器计算最合适,请写在括号里。( )
三、判断题
15.458-99=458-100-1。( )
16.125÷(25×5)=125÷25×5=1。( )
17.欧洲人用“双倍法”计算46×13,是用46的8倍+4倍+1倍。( )
18.因为△+□=〇,●×〇=◎,所以△×●+□×●=◎。( )
19.将算式14×28×25改成28×(14×25),只运用了乘法结合律。( )
四、计算题
20.直接写得数。
21.计算下面各题。(带☆的题要用简便方法计算)
400÷16×5 528-28×11 ☆720÷16÷5
800÷[(197-189)×5] 912-874÷(28+10) ☆36×25
五、解答题
22.刘师傅和张师傅共同加工一批零件,24天正好加工完。刘师傅每天加工82个零件,张师傅每天加工79个零件。这批零件一共有多少个?
23.小军和小琴两人同时从相距2千米的两地相向而行。小军每分钟行120米,小琴每分钟行80米。如果一只狗与小军同时出发,同向而行。当它遇到小琴后,立即回头向小军跑去。这样来回不断,直到小军和小琴相遇为止,这时狗一共跑了4千米。这只狗每分钟行多少米?
24.王老师和张老师同时从家出发去科技馆(如图),王老师步行速度是85米/分,张老师骑行速度是215米/分,12分钟后两人同时到达。沿图中的路线,从王老师家到张老师家的路程是多少米?
25.疫情期间,社区服务人员义务为居民采购蔬菜,购进8筐西红柿和8筐黄瓜,每筐西红柿68千克,每筐黄瓜57千克。请你算一算,购进西红柿和黄瓜一共多少千克?
26.公园有两块花圃(如图)。一块是正方形的种郁金香,另一块是长方形的种菊花。菊花的占地面积比郁金香少多少平方米?
参考答案:
1.C
【分析】乘法分配律是指两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变。据此可知,计算70×4+60×4时,先提相同的因数4,再将剩下部分相加,用这个和乘4,进行简算。则70×4+60×4=(70+60)×4运用了乘法分配律。
【详解】70×4+60×4
=(70+60)×4
=130×4
=520(千米)
他的两种解法实际上运用了乘法分配律。
故答案为:C
【点睛】本题考查学生对乘法分配律的应用和掌握情况。
2.B
【分析】他们从同一起点向相反方向跑封闭的环形跑道,第一次相遇时两人跑的路程就是跑道的长度,所以两人跑的速度和乘相遇的时间就是跑道的长度。
【详解】(3+5)×45
=8×45
=360(米)
操场跑道长360米。
故答案为:B
【点睛】本题考查简单的相遇行程应用题,主要运用行程问题的数量关系来解答。
3.B
【分析】根据乘法分配律计算99×99+99时,先提取公因数99,再将剩下部分相加。用99乘这个和进行简算。则99×99+99=99×100。再比较99×100与100×100的大小即可。
【详解】99×99+99
=99×(99+1)
=99×100
99<100
则99×100<100×100
也就是99×99+99<100×100。
故答案为:B
【点睛】本题关键是熟练掌握乘法分配律,将算式99×99+99变换为99×100。
4.C
【分析】80乘5等于5分钟打字个数,1200减5分钟打字个数等于剩余没打的字数,再除以100即等于还要打字的分钟数。
【详解】(1200-80×5)÷100
=800÷100
=8(分钟)
还要打8分钟才能打完。
故答案为:C
【点睛】本题的关键是读懂题意,理清题中的数量关系,再确定先算什么,最后再算什么。
5.C
【分析】乘法分配律:两个数的差与第三个数相乘,可以把被减数和减数分别同第三个数相乘,再把两个积相减,结果不变;乘法分配律也可以逆运用。
【详解】根据分析可得:a×9-b×9=(a-b)×9。
故答案为:C
【点睛】本题考查的是乘法分配律的灵活运用。
6.B
【分析】乘法分配律:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加;乘法分配律也可以逆运用。
【详解】根据分析可得:78×49+78×51=78×(49+51)。
故答案为:B
【点睛】熟练掌握乘法分配律的定义是解答此题的关键。
7. > = < =
【分析】(1)260×14表示14个260的和,260×10+4表示10个260的和再加上1个4,14个260的和一定大于10个260的和再加上1个4;
(2)一个数连续乘两个数,等于这个数乘后两个数的积;
(3)80÷(4×5)=80÷4÷5,一个数(0除外)除以5的商一定小于这个数乘5的积;
(4)580×47的积等于58×47的积的末尾再加上1个0,470×58的积等于47×58的积的末尾再加上1个0。
【详解】(1)260×14>260×10+4;
(2)320×4×5=320×20;
(3)80÷(4×5)=80÷4÷5,80÷4÷5<80÷4×5,则80÷(4×5)<80÷4×5;
(4)580×47=470×58。
【点睛】算式的大小比较通常是口算或估算出结果再根据结果进行比较,或先找规律或性质,然后再根据规律或性质进行比较。
8.加法交换律和加法结合律
【分析】加法交换率是两个加数交换位置,和不变,公式a+b=b+a;
加法结合率是三个数相加,先把前两个数相加或先把后两个数相加,再加第三个数,和不变,公式a+b+c=(a+b)+c=a+(b+c);
据此判断即可。
【详解】根据题干,★和●两个加数的位置进行了交换,根据加法交换律的意义可知,★+●+▲=●+(★+▲),运用了加法交换律;
算式中加了括号,先把后两个数相加,所以还运用了加法结合律。
【点睛】本题考查了加法交换律和加法结合律的意义。
9.220
【分析】计算12×(★+20)时,运用乘法分配律进行解答,再减去(12×★+20),即可解答。
【详解】12×(★+20)-(12×★+20)
=12×★+20×12-12×★-20
=240-20
=220
这样算出来的得数比原来少了220。
【点睛】此题考查了灵活运用乘法分配律进行简算。
10.(1) 140 90
(2) 58 46
(3) 125 8
(4) 36 36 68 32
【分析】(1)加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。据此解答
(2)乘法交换律:两个数相乘,交换因数的位置,积不变。据此解答
(3)乘法结合律:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。据此解答
(4)乘法分配律是指两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。据此解答
(1)
260+(140+90)=(260+140)+90
(2)
58×46=46×58
(3)
125×27×8=27×(125×8)
(4)
68×36+32×36=(68+32)×36
【点睛】本题解题关键是要熟练掌握运算律并灵活运用。
11. 8 4 125×8×4
【分析】乘法结合律:三个数相乘,先把前两个数相乘或先把后两个数相乘,积不变。据此解答。
【详解】125×32
=125×8×4
=1000×4
=4000
所以计算125×32,可将32变成8×4,将原式变成125×8×4。
【点睛】本题解题关键是要熟练掌握乘法结合律的特点。
12. 4 5 500 4 7 700 4 9 900
【分析】乘法结合律:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。用字母表示为:a×b×c=a×(b×c)。观察前三个式子发现,第二个因数都分成4与一个数的积。据此解答。
【详解】25×20=25×4×5=500;
25×28=25×4×7=700;
25×36=25×4×9=900。
【点睛】解答此题的关键是熟练掌握乘法结合律并且仔细观察式子特点,然后找出规律,根据规律填出同类算式的结果。
13. 145 10 乘法分配律
【分析】观察竖式可知,箭头部分是145与12的十位上1的乘积,即145×10,表示1450,290是145与2的乘积,然后把它们相加即等于145×12的积,所以乘法笔算的过程应用了乘法分配律;据此即可解答。
【详解】根据分析可知,竖式中,箭头部分算的是145×10,乘法笔算的过程应用了乘法分配律。
【点睛】本题主要考查了学生对整数乘法和乘法分配律的掌握及灵活运用。
14.456×37
【分析】由题意可得, 370÷5÷2用除法的性质先计算5×2=10,再计算370÷10=37;9998×346×0×12456中乘数有0,则结果直接为0;456×37需要用计算器进行计算。
【详解】在计算370÷5÷2、9998×346×0×12456、456×37时,456×37用计算器计算最合适。
【点睛】此题考查了乘除法的应用,关键是先看各算式是否能用简便算法计算。
15.×
【分析】458-99,因为99接近整百,可以把它先看做100,就是458-100,因为100比99多1,这样一来就多减去了1,再在式子的后面把多减去的加回来,就是458-100+1。
【详解】根据分析可知:
458-99=458-100+1,原题错误。
故答案为:×
【点睛】简便算法变化多端,要理解算理,要熟悉数字之间存在的关系,再运用简便算法。
16.×
【分析】除法性质:一个数连续除以两个数,可以先把后两个数相乘,再相除。如a÷b÷c=a÷(b×c);据此解答即可。
【详解】125÷(25×5)
=125÷25÷5
=5÷5
=1
125÷(25×5)≠125÷25×5,所以原题计算错误。
故答案为:×
【点睛】本题考查了学生对于整数除法性质的理解及运用。
17.√
【分析】把13分解为8、4、1的和,再分别计算出46的8倍,46的4倍,46的1倍,最后将所得积相加即可。
【详解】46×13
=46×(8+4+1)
=46×8+46×4+46×1
故答案为:√
【点睛】一个数的几倍,即用这个数乘几。
18.√
【分析】利用等量代换,把等式△+□=〇代入到算式●×〇中去,利用乘法分配律计算后判断即可。
【详解】将等式△+□=〇代入算式●×〇,得:
●×〇=●×(△+□)
=△×●+□×●
=◎
所以原题的说法正确。
故答案为:√
【点睛】本题是一道简单的等量代换问题,“〇”的代换是解决本题的关键。
19.×
【分析】乘法结合律为:在乘法算式中,先将前两个数相乘,或先将后两个数相乘,积不变;乘法交换律是交换因数的位置,积不变;算式14×28×25=28×(14×25)首先运用了乘法交换律,然后运用了乘法结合律。
【详解】由分析得:
将算式14×28×25改成28×(14×25),运用了乘法交换律和乘法结合律。
故答案为:×
【点睛】我们要牢记乘法交换律、乘法结合律的概念,根据概念灵活运用,同时要注意简便算法经常综合在一起使用。
20.7;80;5;36;130
21;101;2000;110;0
【解析】略
21.125;220;9
20;889;900
【分析】400÷16×5按照从左到右的顺序计算;
528-28×11先算乘法再算减法;
720÷16÷5运用除法的性质简便计算;
800÷[(197-189)×5] 先算小括号里减法,再算中括号里乘法,最后算除法;
912-874÷(28+10)先算小括号里加法,再算除法,最后算减法;
36×25,把36换成9×4,即原式变为:9×4×25,运用乘法结合律简便计算。
【详解】400÷16×5
=25×5
=125
528-28×11
=528-308
=220
720÷16÷5
=720÷(16×5)
=720÷80
=9
800÷[(197-189)×5]
=800÷[8×5]
=800÷40
=20
912-874÷(28+10)
=912-874÷38
=912-23
=889
36×25
=9×4×25
=9×(4×25)
=9×100
=900
22.3864个
【分析】用刘师傅平均每天加工零件个数加上张师傅平均每天加工零件个数,求出两人平均每天加工零件总个数。再乘加工天数,即可求出这批零件总个数。
【详解】(82+79)×24
=161×24
=3864(个)
答:这批零件一共有3864个。
【点睛】本题先求出两人平均每天加工零件总个数,再根据工作总量=工作效率×工作时间解答。
23.400米
【分析】由于无论狗在两人之间跑了多少个来回,狗所走的时间与小军、小琴两人相遇所用的时间是一样的,问题转化为求小军、小琴两人相遇所用的时间,也就是狗行走的时间;再根据路程÷时间=速度,这只狗每分钟行多少米,即可解答题目。
【详解】2千米=2000米
2000÷(120+80)
=2000÷200
=10(分钟)
4千米=4000米
4000÷10=400(米)
答:这只狗每分钟行400米。
【点睛】本题属于相遇问题,要求小狗跑的速度,已知小狗跑的路程,关键是得到小狗跑的时间,然后用关系式:路程÷时间=速度进行解答。
24.3600米
【详解】根据速度×时间=路程,用王老师、张老师的速度之和乘两人同时到达科技馆用的时间,即可求出从王老师家到张老师家的路程是多少米。
【解答】(85+215)×12
=300×12
=3600(米)
答:从王老师家到张老师家的路程是3600米。
【点睛】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
25.1000千克
【分析】用68乘8,求出8筐西红柿的质量;用57乘8,求出8筐黄瓜的质量;再用8筐西红柿的质量加上8筐黄瓜的质量,即68×8+57×8,此算式可以根据乘法分配律进行简算,则改写成(68+57)×8,据此解答。
【详解】68×8+57×8
=(68+57)×8
=125×8
=1000(千克)
答:购进西红柿和黄瓜一共1000千克。
【点睛】本题考查了学生对乘法分配律的掌握与运用。
26.550平方米
【分析】正方形的边长是55米,55乘55即可求出正方形面积,长方形菊花地的长是55米,宽是45米,55乘45即可求出菊花地的面积,再用郁金香地的面积减菊花地的面积即可解答。
【详解】55×55-55×45
=55×(55-45)
=55×10
=550(平方米)
答:菊花的占地面积比郁金香少550平方米。
【点睛】正方形面积=边长×边长,长方形面积=长×宽。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
