17.4零指数幂与负整指数幂.[下学期]
文档属性
| 名称 | 17.4零指数幂与负整指数幂.[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 387.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-24 11:55:00 | ||
图片预览






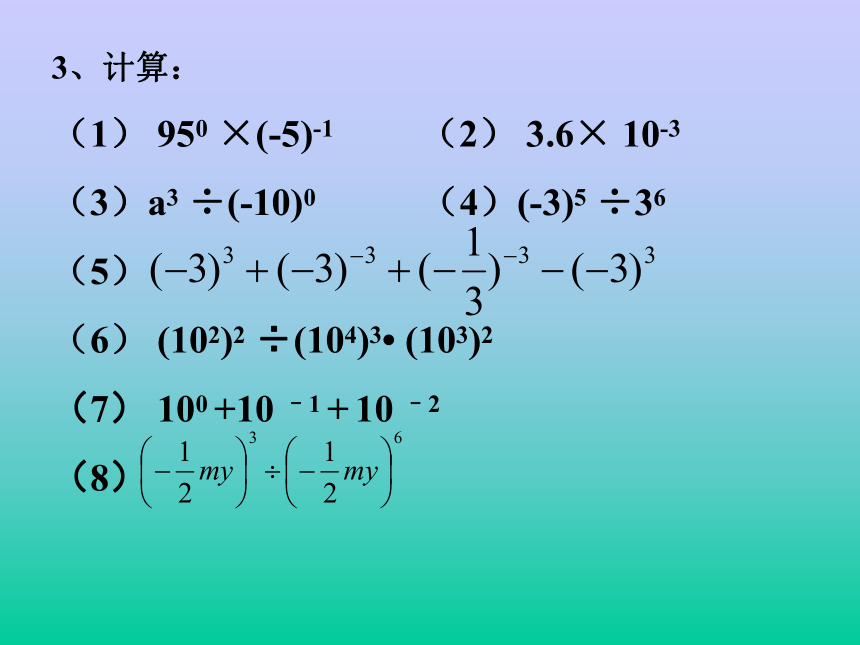

文档简介
课件24张PPT。课 时 计 划
第 周 星期五 第1、4节 2005年8月12日
课题:21.5零指数幂与负整指数幂(1)
教学目标:
探索零指数幂、负整指数幂的意义,会运用其意义进行有关的计算。
教材分析:
重点:对提出零指数幂、负整指数幂的新的结果的探究过程
难点:探究过程的体会,继承旧知识,得出新结果。
教具:多媒体
教学方法:讨论式教学
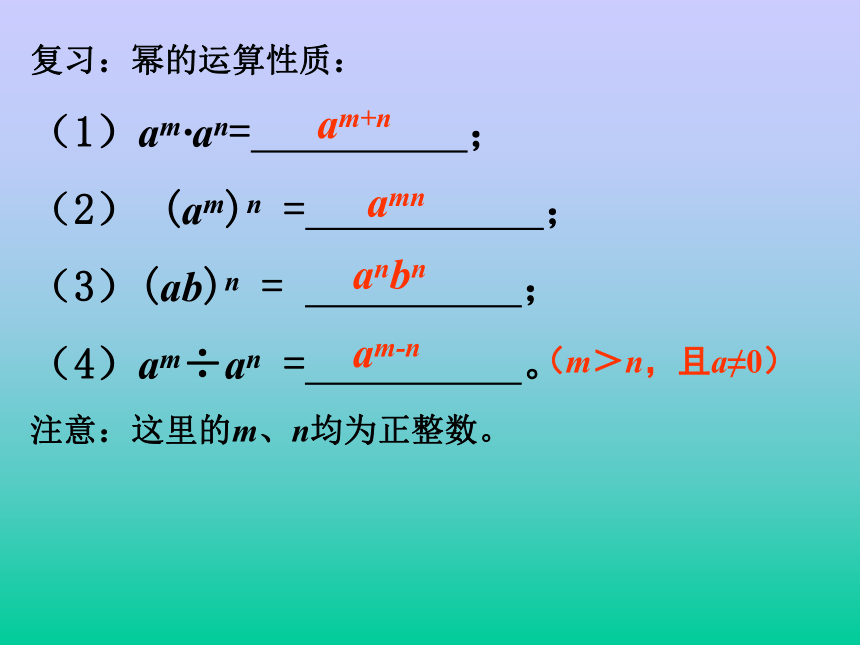
教学过程:零指数幂与负整指数幂(1)复习:幂的运算性质:
(1)am·an= ;
(2) (am)n = ;
(3)(ab)n = ;
(4)am÷an = 。
注意:这里的m、n均为正整数。am+nam-namnanbn(m>n,且a≠0)a0 =1(a 0)≠请用语言叙述由此我们规定 任何不等于零的数的零次幂都等于1。问题2:计算下列各式
(1)34÷35; (2)a4÷a6。由此可知:问题3:猜想 a-p=? 我们规定:a0 — 零指数幂;a–p — 负指数幂。语言叙述为:任何不等于零的数的-p(p 是正整数)次幂,等于这个数的p次幂的倒数。3、计算:
(1) 950 ×(-5)-1 (2) 3.6× 10-3
(3)a3 ÷(-10)0 (4)(-3)5 ÷36
(5)
(6) (102)2 ÷(104)3? (103)2
(7) 100 +10 –1 + 10 –2
(8)4、用小数表示下列各数:
①10-4; ② 1.6×10-3;
③2.1×10-5; ④-3.2×10-5。
5、计算:
(1)a2×a-3;(2)(a×b)-3;(3)(a-3)2。
6、计算下列各式,并把结果化为只含有正整数指数幂的形式:
(1)(a-3)2(ab2)-3; (2)(2mn2)-2(m-2n-1)-3;
(3)(x-3yz-2)2; (4)(a3b-1)-2(a-2b2)2;
(5)(2m2n-3)3(-mn-2)-2。小结2.同底数幂的除法法则
am ÷an = a m-n (a≠0,m、n都是正整数,且m>n)中的条件可以改为:
(a≠0,m、n都是正整数)课 时 计 划
第 周 星期五 第2、5节 2005年8月12日
课题:21.5零指数幂与负整指数幂(2)
教学目标:
分清绝对值大于1及绝对值小于1的数的科学记数法
教材分析:
重点:探究绝对值大于1及绝对值小于1的数的科学记数法的异同点,以及处理方法。
难点:科学记数法中的指数与小数点后面零的个数的关系。
教具:多媒体
教学方法:探究、讨论式教学
教学过程:问题3:用整数或小数表示下列各数:(1)9.932×103(3)7.21×10 -5(2)-4.21×107(4) - 3.021×10 –3= 9932= 0.0000721= -42100000= -0.003021=7.21×0.00001= - 3.021×0.001较大数的科学记数法:a ×10 n(1≤| a |<10,n为正整数) 9.932×103 -4.21×1077.21×10 – 5 - 3.021×10 – 3 较小数的科学记数法:a ×10 -n(1≤| a |<10,n为正整数) = 0.0000721= -0.003021nn(n为正整数)问题4:计算10000
1000
100
10
1
0.1
0.01
0.001
0.0001练习4:
1、 把下列各数表示成 a ×10n ( 1≤a<10,n为整数)的形式:
12000; (2) 0.0021; (3) 0.0000501。
2、用科学记数法表示:
(1)0.000 02; (2)0.000 003;
(3)-0.000 034; (4)-0.000 006 4;
(5)0.000 0314; (6)2013000。
3、用小数表示下列各数:
(1)3.5×10-5; (2)– 9.32×10–8。
4、课本P20 练习2 习题21.5 35、计算下列各题,并把结果用科学记数法的形式表示:
(1)2.1×103×3.5×104;
(2)7.85×103×9.58×10-6;
(3)5×10-3×6×10-8;
(4)(10.01×103)÷(2×104)(结果保留3个有效数字)。小结2.同底数幂的除法法则
am ÷an = a m-n (a≠0,m、n都是正整数,且m>n)中的条件可以改为:
(a≠0,m、n都是正整数)a ×10 -n(1≤| a |<10,n为正整数) a ×10 n(1≤| a |<10,n为正整数) 3、科学记数法:nn小测: 1、选择 (1)计算2-1结果是 ( ) A、 -2 B、 2 C、 -1/2 D、 1/2 (2) 各式正确的是( ) A、 x2p ÷xp=x2 B、 xmx-n=xm-n C、 xm-n=xm-x-n D、 x6 ÷x2=x3 (3)下列各式正确的个数是( ) ① (0.1)0=1 ② 10-3=0.0001 ③ 10-5= 0.00001 ④ (6-3 ╳ 2)0=1 A、 1 个 B、 2个 C、 3个 D、 4个
(4)各式错误的是( )
A、 x12 ÷x2 ÷x2 =x8 B、 x·x6 ÷( x3)2 = x
C、( xy)5 ÷(xy3)= ( xy)2 D、 x10 ÷(x4÷x2) = x82、填空
(1)a3 ÷a=______ (a3)2 ÷a3=______
(2)当x_____时 (x-1)0=1
(3)空气的密度是1.239×10-3克/厘米3,用小数表示 。
(4)声音的强度单位为分贝,通常讲话时声音是50分贝,它表示声音的强度是105,摩托车发出声音是110分贝,它表示声音的强度是1011,喷气式飞机发出声音是150分贝,其强度是摩托车发出声音的_____倍,讲话声音的_____倍。练习5:
1、用分数表示:
7-2= ______ 5-3 = ____
(-3)-1=_____ (0.1)-2=_____
2、用小数表示:
3×10-6=_______ 8.7 × 10-3 =________
50 × 10-2=________ 3、求解
(1)如果(3/2)y=4/9,求y值? (2)(-10)2+(-10)0+10-2 ╳ (-102) (3)月球质量约为7.351 ╳ 1025克,地球质量约为5.977 ╳ 1027克,地球质量约为月球质量多少倍? (4)小明家的电脑用的是奔腾Ⅳ处理器,开机1小时运行次数是2.64 ╳ 1012次,运算频率(每秒运算次数)是多少?思考题:1、若(y-5)0 无意义,且3x+2y=1,求x,y的值.
2、若xm = 2 , xn =4,x3m -2n的值.
3、求2750 ÷(-9)74的值.
4、0.8× 10-4 用小数表示为______.
5、用科学记数法表示:
0.0000653 -0.00985 5690000布置作业:
作业练习卷8
板书设计:
课题
1、零指数幂
2、负整指数幂 投影幕
3、科学记数法
学生板演
第 周 星期五 第1、4节 2005年8月12日
课题:21.5零指数幂与负整指数幂(1)
教学目标:
探索零指数幂、负整指数幂的意义,会运用其意义进行有关的计算。
教材分析:
重点:对提出零指数幂、负整指数幂的新的结果的探究过程
难点:探究过程的体会,继承旧知识,得出新结果。
教具:多媒体
教学方法:讨论式教学
教学过程:零指数幂与负整指数幂(1)复习:幂的运算性质:
(1)am·an= ;
(2) (am)n = ;
(3)(ab)n = ;
(4)am÷an = 。
注意:这里的m、n均为正整数。am+nam-namnanbn(m>n,且a≠0)a0 =1(a 0)≠请用语言叙述由此我们规定 任何不等于零的数的零次幂都等于1。问题2:计算下列各式
(1)34÷35; (2)a4÷a6。由此可知:问题3:猜想 a-p=? 我们规定:a0 — 零指数幂;a–p — 负指数幂。语言叙述为:任何不等于零的数的-p(p 是正整数)次幂,等于这个数的p次幂的倒数。3、计算:
(1) 950 ×(-5)-1 (2) 3.6× 10-3
(3)a3 ÷(-10)0 (4)(-3)5 ÷36
(5)
(6) (102)2 ÷(104)3? (103)2
(7) 100 +10 –1 + 10 –2
(8)4、用小数表示下列各数:
①10-4; ② 1.6×10-3;
③2.1×10-5; ④-3.2×10-5。
5、计算:
(1)a2×a-3;(2)(a×b)-3;(3)(a-3)2。
6、计算下列各式,并把结果化为只含有正整数指数幂的形式:
(1)(a-3)2(ab2)-3; (2)(2mn2)-2(m-2n-1)-3;
(3)(x-3yz-2)2; (4)(a3b-1)-2(a-2b2)2;
(5)(2m2n-3)3(-mn-2)-2。小结2.同底数幂的除法法则
am ÷an = a m-n (a≠0,m、n都是正整数,且m>n)中的条件可以改为:
(a≠0,m、n都是正整数)课 时 计 划
第 周 星期五 第2、5节 2005年8月12日
课题:21.5零指数幂与负整指数幂(2)
教学目标:
分清绝对值大于1及绝对值小于1的数的科学记数法
教材分析:
重点:探究绝对值大于1及绝对值小于1的数的科学记数法的异同点,以及处理方法。
难点:科学记数法中的指数与小数点后面零的个数的关系。
教具:多媒体
教学方法:探究、讨论式教学
教学过程:问题3:用整数或小数表示下列各数:(1)9.932×103(3)7.21×10 -5(2)-4.21×107(4) - 3.021×10 –3= 9932= 0.0000721= -42100000= -0.003021=7.21×0.00001= - 3.021×0.001较大数的科学记数法:a ×10 n(1≤| a |<10,n为正整数) 9.932×103 -4.21×1077.21×10 – 5 - 3.021×10 – 3 较小数的科学记数法:a ×10 -n(1≤| a |<10,n为正整数) = 0.0000721= -0.003021nn(n为正整数)问题4:计算10000
1000
100
10
1
0.1
0.01
0.001
0.0001练习4:
1、 把下列各数表示成 a ×10n ( 1≤a<10,n为整数)的形式:
12000; (2) 0.0021; (3) 0.0000501。
2、用科学记数法表示:
(1)0.000 02; (2)0.000 003;
(3)-0.000 034; (4)-0.000 006 4;
(5)0.000 0314; (6)2013000。
3、用小数表示下列各数:
(1)3.5×10-5; (2)– 9.32×10–8。
4、课本P20 练习2 习题21.5 35、计算下列各题,并把结果用科学记数法的形式表示:
(1)2.1×103×3.5×104;
(2)7.85×103×9.58×10-6;
(3)5×10-3×6×10-8;
(4)(10.01×103)÷(2×104)(结果保留3个有效数字)。小结2.同底数幂的除法法则
am ÷an = a m-n (a≠0,m、n都是正整数,且m>n)中的条件可以改为:
(a≠0,m、n都是正整数)a ×10 -n(1≤| a |<10,n为正整数) a ×10 n(1≤| a |<10,n为正整数) 3、科学记数法:nn小测: 1、选择 (1)计算2-1结果是 ( ) A、 -2 B、 2 C、 -1/2 D、 1/2 (2) 各式正确的是( ) A、 x2p ÷xp=x2 B、 xmx-n=xm-n C、 xm-n=xm-x-n D、 x6 ÷x2=x3 (3)下列各式正确的个数是( ) ① (0.1)0=1 ② 10-3=0.0001 ③ 10-5= 0.00001 ④ (6-3 ╳ 2)0=1 A、 1 个 B、 2个 C、 3个 D、 4个
(4)各式错误的是( )
A、 x12 ÷x2 ÷x2 =x8 B、 x·x6 ÷( x3)2 = x
C、( xy)5 ÷(xy3)= ( xy)2 D、 x10 ÷(x4÷x2) = x82、填空
(1)a3 ÷a=______ (a3)2 ÷a3=______
(2)当x_____时 (x-1)0=1
(3)空气的密度是1.239×10-3克/厘米3,用小数表示 。
(4)声音的强度单位为分贝,通常讲话时声音是50分贝,它表示声音的强度是105,摩托车发出声音是110分贝,它表示声音的强度是1011,喷气式飞机发出声音是150分贝,其强度是摩托车发出声音的_____倍,讲话声音的_____倍。练习5:
1、用分数表示:
7-2= ______ 5-3 = ____
(-3)-1=_____ (0.1)-2=_____
2、用小数表示:
3×10-6=_______ 8.7 × 10-3 =________
50 × 10-2=________ 3、求解
(1)如果(3/2)y=4/9,求y值? (2)(-10)2+(-10)0+10-2 ╳ (-102) (3)月球质量约为7.351 ╳ 1025克,地球质量约为5.977 ╳ 1027克,地球质量约为月球质量多少倍? (4)小明家的电脑用的是奔腾Ⅳ处理器,开机1小时运行次数是2.64 ╳ 1012次,运算频率(每秒运算次数)是多少?思考题:1、若(y-5)0 无意义,且3x+2y=1,求x,y的值.
2、若xm = 2 , xn =4,x3m -2n的值.
3、求2750 ÷(-9)74的值.
4、0.8× 10-4 用小数表示为______.
5、用科学记数法表示:
0.0000653 -0.00985 5690000布置作业:
作业练习卷8
板书设计:
课题
1、零指数幂
2、负整指数幂 投影幕
3、科学记数法
学生板演
