零指数幂与负整指数幂[下学期]
图片预览





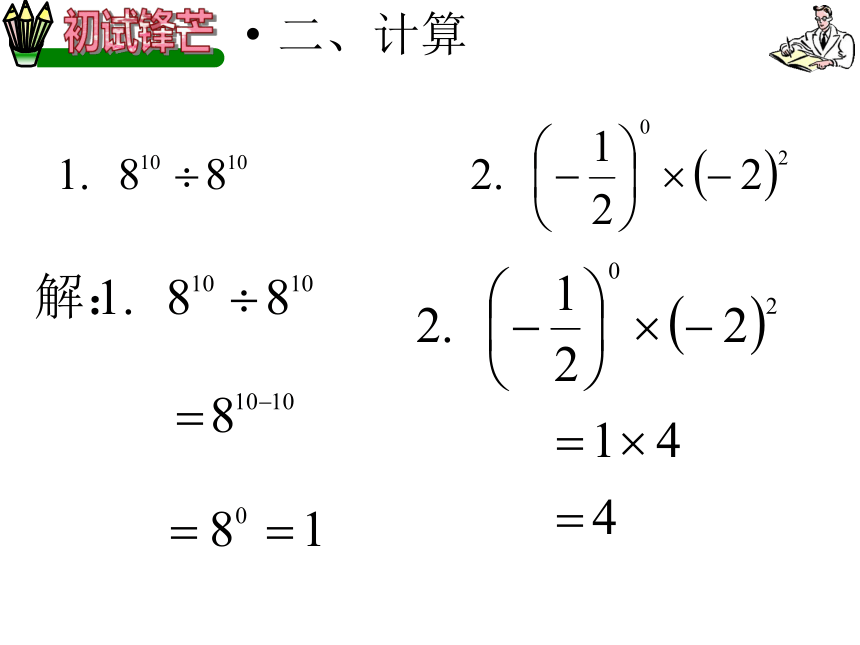

文档简介
课件24张PPT。1.使学生掌握不等于零的零次幂的意义.
2.使学生掌握 (a≠0,n是正整数)并会运用它进行计算.
3.通过探索,让学生会从特殊到一般的方法是研究数学的一个重要方法.
教学目标重点、难点不等于零的零次幂的意义以及理解和应用负整指数幂的性质是本节课的重点也是难点.§21.5 零指数幂与负整指数幂③ ④ ①2.整数指数幂的运算性质:
若m,n为整数,且a≠0,b≠0,则有② §21.5 零指数幂与负整指数幂1、零指数幂与负整指数幂一、创设问题情境:我们学习同底数幂的除法公式am÷an=am-n时,有一个附加条件:m>n,即被除数的指数大于除数的指数。当被除数的指数不大于除数的指数,即m=n或m【同底数幂的除法法则】【除法的意义】1.我们先考察被除数的指数等于除数的指数的情况。零的零次幂没有意义!做一做一、判断正误:
×√√√√做一做二、计算
…………结论:……
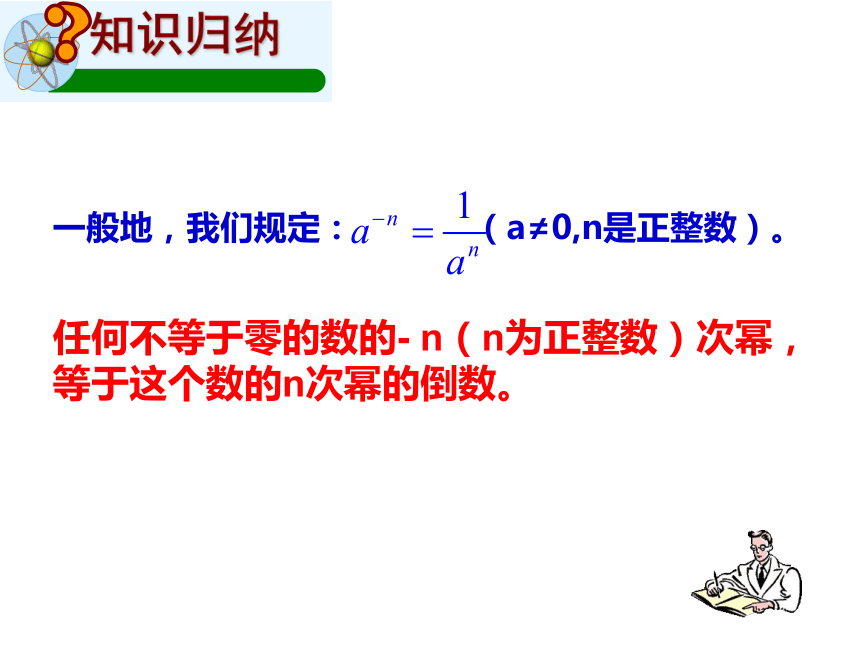
【同底数幂的除法法则】【除法的意义】2.再考察被除数的指数小于除数的指数的情况。任何不等于零的数的- n(n为正整数)次幂,
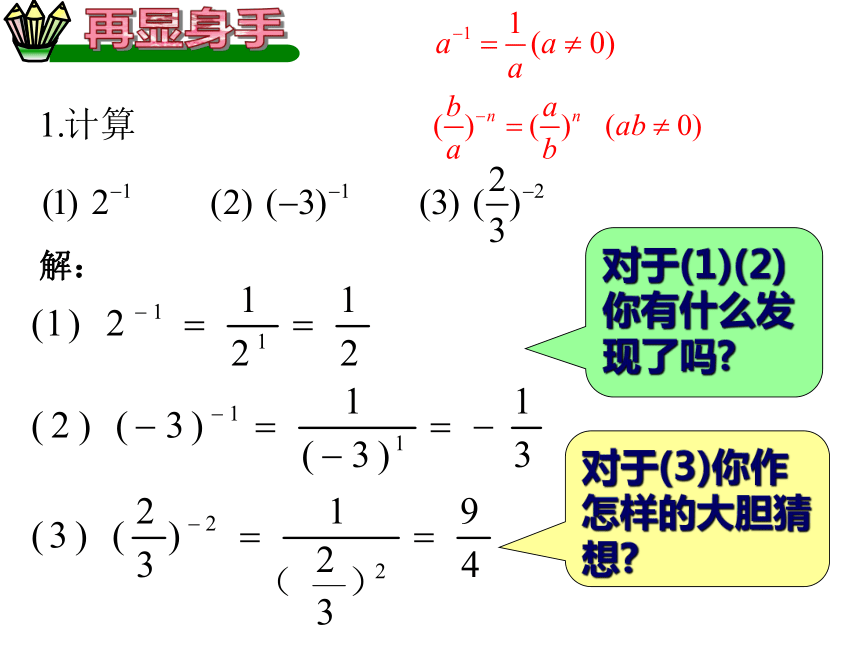
等于这个数的n次幂的倒数。对于(1)(2)你有什么发现了吗?
对于(3)你作怎样的大胆猜想?
解:1.用小数或分数表示下列各数 再攀高峰1.同底数幂的乘法的性质是什么?怎样用式子表示?2.幂的乘方、积的乘方的性质是什么?
怎样用式子表示?同底数幂相乘,底数不变,指数相加。am·an=am+n(am)n=amn幂的乘方,底数不变,指数相乘。(ab)n=anbn积的乘方等于各因数乘方的积。在以前所学习过的幂的性质中,m、n都是正整数,引进了零指数幂和负整数幂,指数的范围扩大到了全体整数,上述幂的性质是否依然成立?四、幂的性质(指数为全体整数):3、判断下列式子是否成立?如果成立,你能给出证明吗?(1)a2·a- 3=a2+(-3)(2) (a·b)- 3=a- 3b- 3(3) (a- 3)2=a(-3)×2证明:4、你能从上面的尝试中得到什么结论?am·an=am+n(am)n=amn(ab)n=anbn(a≠0, b≠0,m、n都是整数)·5、试一试:计算下列各式,并且把计算的结果化为
只含有正整数幂的形式。(1) a2b3 (2a-1b)3(2) (a-2)- 3(bc-1)3=a2b3 (23a-1×3b3)=8a2-3b3+3= 8a-1b6= a- 2×(- 3)b3c-1×3= a6b3c-3(2)(3)例1.(1) 解:(1)原式4422332)()()()(abcabccba·-·-=分子、分母分别乘方例1.(1) (2)把负整数指数写成正整数指数的形式积的乘方(3)同底数幂相乘,底数不变指数相加结果化为只含有正整数指数的形式2、科学记数法1.掌握幂的性质(指数为全体整数)并会用于计算.
2.能用科学记数法表示一些绝对值较小的数.教学目标重点、难点1.重点:幂的性质(指数为全体整数)并会用于计算以及用科学记数法表示一些绝对值较小的数.
2.难点:理解和应用整数指数幂的性质.2、科学记数法问题1:什么叫做科学记数法?如:35000=3.5×10 4问题2:能不能利用10的负整数幂,用科学记数法表示一些绝对值较小的数?试一试:2、已知1纳米= 米,一个纳米粒子的直径是35纳米,它等于多少米?请用科学记数法表示。把一个绝对值大于10的数表示成a×10n的形式,其中n是正整数,1 ∣a ∣<10,这样的记数法叫做科学记数法。我们可以将它们表示成a×10-n的形式,
其中n是正整数, 1 ∣a ∣<10。如:0.000035=3.5×10?课堂练习1、用科学记数法表示:(1)256000(2)0.00005(3)-0.000056(4)450×0.00000012、计算下列各式,并且把结果化为只含有正整数指数幂的形式(1) (a- 3·a- 2)2(2) (ab)- 3·(2a2)2(3) (x- 1y - 2z- 3)2(4) (3mn -2)- 3 · (-mn- 3)23、已知一种细菌的半径是0.00004米,试用科学记数法表示(单位仍用米)。4、地球上陆地面积约为149000000 km2,用科学记数法把它表示出来(单位仍用km2)2、课堂练习:1.用小数表示下列各数:(1)10- 4= ; (3) – 6.05×(6.05)0= ; (2) 4×10- 6= ;(4)1.23×10-1= ;2.填空:(1)5- 1= ; (2)1- 9 = ; (3)(- 0.526)0= ; (4)10- 3= ; (5)am+n÷am+n = ;(a≠0) (6) (-7)0×10-2= ; 3.用小数表示下列各数:(1) 4×10- 4(2) 3.1×10- 6(3) 8.05×10- 7(4) 1.205×10-2(5) 3.13×10- 1(6) 5.16×10 0 不等于零的数的零次幂的意义以及理解和应
用负整数指数幂的性质是本节课的重点也是难点。通过探索,让学生体会到从特殊到一般的方法
是研究数学的一个重要方法。 教学反思
2.使学生掌握 (a≠0,n是正整数)并会运用它进行计算.
3.通过探索,让学生会从特殊到一般的方法是研究数学的一个重要方法.
教学目标重点、难点不等于零的零次幂的意义以及理解和应用负整指数幂的性质是本节课的重点也是难点.§21.5 零指数幂与负整指数幂③ ④ ①2.整数指数幂的运算性质:
若m,n为整数,且a≠0,b≠0,则有② §21.5 零指数幂与负整指数幂1、零指数幂与负整指数幂一、创设问题情境:我们学习同底数幂的除法公式am÷an=am-n时,有一个附加条件:m>n,即被除数的指数大于除数的指数。当被除数的指数不大于除数的指数,即m=n或m
×√√√√做一做二、计算
…………结论:……
【同底数幂的除法法则】【除法的意义】2.再考察被除数的指数小于除数的指数的情况。任何不等于零的数的- n(n为正整数)次幂,
等于这个数的n次幂的倒数。对于(1)(2)你有什么发现了吗?
对于(3)你作怎样的大胆猜想?
解:1.用小数或分数表示下列各数 再攀高峰1.同底数幂的乘法的性质是什么?怎样用式子表示?2.幂的乘方、积的乘方的性质是什么?
怎样用式子表示?同底数幂相乘,底数不变,指数相加。am·an=am+n(am)n=amn幂的乘方,底数不变,指数相乘。(ab)n=anbn积的乘方等于各因数乘方的积。在以前所学习过的幂的性质中,m、n都是正整数,引进了零指数幂和负整数幂,指数的范围扩大到了全体整数,上述幂的性质是否依然成立?四、幂的性质(指数为全体整数):3、判断下列式子是否成立?如果成立,你能给出证明吗?(1)a2·a- 3=a2+(-3)(2) (a·b)- 3=a- 3b- 3(3) (a- 3)2=a(-3)×2证明:4、你能从上面的尝试中得到什么结论?am·an=am+n(am)n=amn(ab)n=anbn(a≠0, b≠0,m、n都是整数)·5、试一试:计算下列各式,并且把计算的结果化为
只含有正整数幂的形式。(1) a2b3 (2a-1b)3(2) (a-2)- 3(bc-1)3=a2b3 (23a-1×3b3)=8a2-3b3+3= 8a-1b6= a- 2×(- 3)b3c-1×3= a6b3c-3(2)(3)例1.(1) 解:(1)原式4422332)()()()(abcabccba·-·-=分子、分母分别乘方例1.(1) (2)把负整数指数写成正整数指数的形式积的乘方(3)同底数幂相乘,底数不变指数相加结果化为只含有正整数指数的形式2、科学记数法1.掌握幂的性质(指数为全体整数)并会用于计算.
2.能用科学记数法表示一些绝对值较小的数.教学目标重点、难点1.重点:幂的性质(指数为全体整数)并会用于计算以及用科学记数法表示一些绝对值较小的数.
2.难点:理解和应用整数指数幂的性质.2、科学记数法问题1:什么叫做科学记数法?如:35000=3.5×10 4问题2:能不能利用10的负整数幂,用科学记数法表示一些绝对值较小的数?试一试:2、已知1纳米= 米,一个纳米粒子的直径是35纳米,它等于多少米?请用科学记数法表示。把一个绝对值大于10的数表示成a×10n的形式,其中n是正整数,1 ∣a ∣<10,这样的记数法叫做科学记数法。我们可以将它们表示成a×10-n的形式,
其中n是正整数, 1 ∣a ∣<10。如:0.000035=3.5×10?课堂练习1、用科学记数法表示:(1)256000(2)0.00005(3)-0.000056(4)450×0.00000012、计算下列各式,并且把结果化为只含有正整数指数幂的形式(1) (a- 3·a- 2)2(2) (ab)- 3·(2a2)2(3) (x- 1y - 2z- 3)2(4) (3mn -2)- 3 · (-mn- 3)23、已知一种细菌的半径是0.00004米,试用科学记数法表示(单位仍用米)。4、地球上陆地面积约为149000000 km2,用科学记数法把它表示出来(单位仍用km2)2、课堂练习:1.用小数表示下列各数:(1)10- 4= ; (3) – 6.05×(6.05)0= ; (2) 4×10- 6= ;(4)1.23×10-1= ;2.填空:(1)5- 1= ; (2)1- 9 = ; (3)(- 0.526)0= ; (4)10- 3= ; (5)am+n÷am+n = ;(a≠0) (6) (-7)0×10-2= ; 3.用小数表示下列各数:(1) 4×10- 4(2) 3.1×10- 6(3) 8.05×10- 7(4) 1.205×10-2(5) 3.13×10- 1(6) 5.16×10 0 不等于零的数的零次幂的意义以及理解和应
用负整数指数幂的性质是本节课的重点也是难点。通过探索,让学生体会到从特殊到一般的方法
是研究数学的一个重要方法。 教学反思
