17.3 可化为一元一次方程的分式方程[下学期]
文档属性
| 名称 | 17.3 可化为一元一次方程的分式方程[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 643.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-19 00:34:00 | ||
图片预览





文档简介
课件17张PPT。甲乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,求甲、乙每小时各做多少个?问题设甲每小时做x个零件,那么乙每小时做(x-6)个。甲做90个所用的时间为:乙做60个所用的时间为:根据题意,列出方程为:分母里含有未知数的方程叫做分式方程。以前我们所学过的方程都是整式方程分式方程的主要特征:(1)含有分式
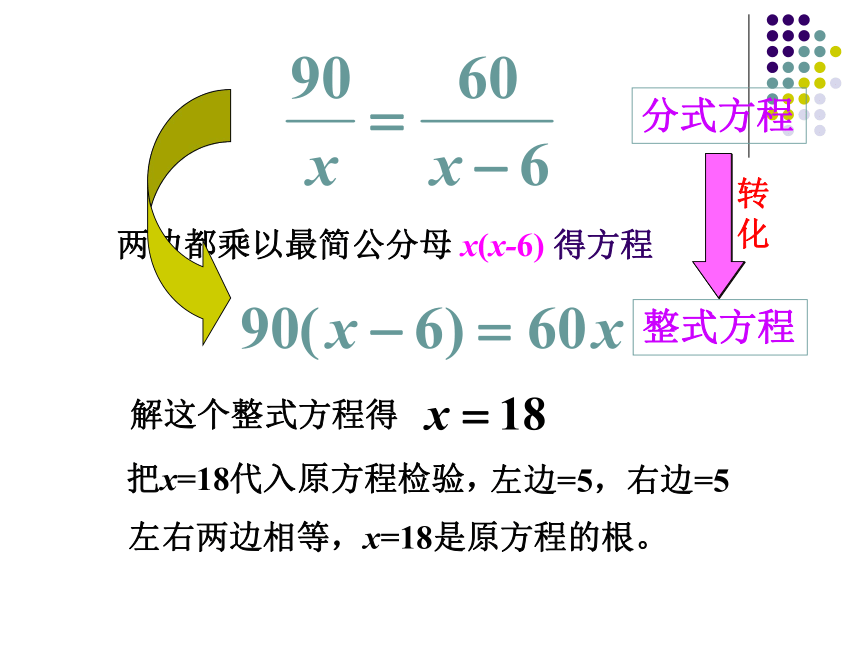
(2)分母中含有未知数 下列方程中哪些是分式方程?两边都乘以最简公分母 x(x-6) 得方程解这个整式方程得分式方程整式方程转化把x=18代入原方程检验,左边=5,右边=5左右两边相等,x=18是原方程的根。可化为一元一次方程的分式方程解方程:两边都乘以最简公分母 (x+1)(x-1) 得整式方程解这个整式方程得x=1究竟是不是原方程的根?把x=1代入原方程检验x=1使某些分式的分母的值为零也就是使分式 和 没有意义∴ x=1不是原方程的根,原分式方程无解。x=18是原方程的根x(x-6)检验化解x=1不是原方程的根(x+1)(x-1)化解检验(1)为了解分式方程,就要把它化为整式方程; 分式方程的两边乘以同一个含有未知数的整式,这个整式一般取分式方程中各分式的最简公分母。(2)这样得到的整式方程的解有时与原分式方程
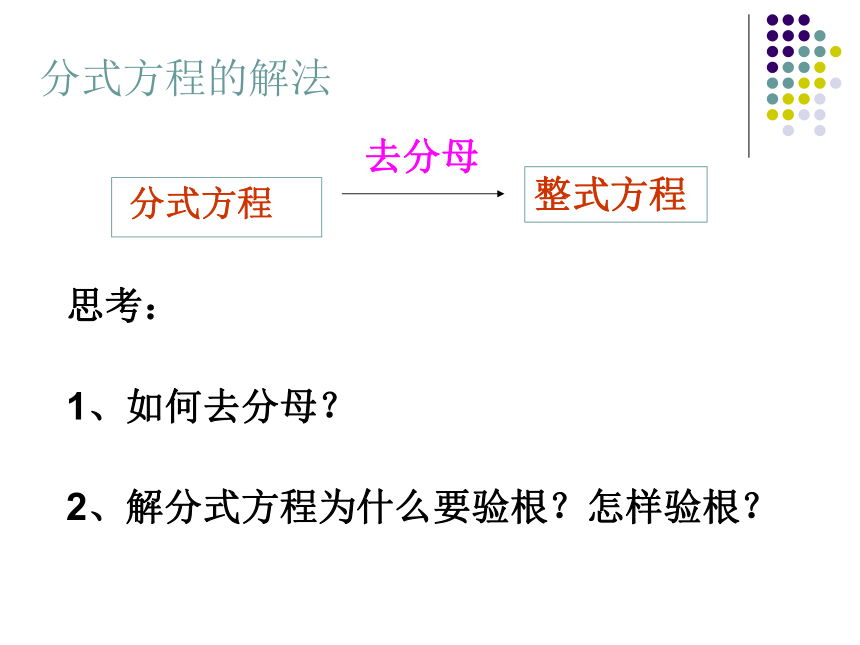
的解相同;有时与原分式方程的解不同。分式方程的解法 分式方程 整式方程 去分母思考:
1、如何去分母?
2、解分式方程为什么要验根?怎样验根?怎样进行检验呢?方法一:把整式方程的根代入原方程,看它是否使原分式方程中的分式有意义;方法二:把整式方程的根代入最简公分母,如果最简公分母的值等于0,则产生了增根,如果最简公分母的值不等于0,则原方程没有产生增根。增根 在方程变形时,有时可能产生不适合原方程的根,这种根叫做原方程的增根。 因为解分式方程时可能会产生增根,所以解分式方程必需检验。例1解方程:例2解方程:解题回顾1、在方程的两边都乘以最简公分母,
约去分母,化成整式方程 ;2、解这个整式方程 ;3、把整式方程的根代入最简公分母,看结
果是不是零,使最简公分母为零的根是原
方程的增根,必须舍去。解分式方程的注意点:(1)去分母时,先确定最简公分母;若分母
是多项式,要进行因式分解;
(2)去分母时,不要漏乘不含分母的项;
(3)最后不要忘记验根。1、判断:小结1. 分式方程的概念:2. 可化为一元一次方程的分式方程的解题步骤:分母里含有未知数的方程叫做分式方程。一化二解三检验作业课本第101页第1题,第102页第1题中(1)、(2)小题判断下列解法是否正确:21解答题: 关于x的方程
无解,试求m的值。 它们有区别吗?有联系吗?=去分母:等式基本性质2 通分:分式基本性质
(2)分母中含有未知数 下列方程中哪些是分式方程?两边都乘以最简公分母 x(x-6) 得方程解这个整式方程得分式方程整式方程转化把x=18代入原方程检验,左边=5,右边=5左右两边相等,x=18是原方程的根。可化为一元一次方程的分式方程解方程:两边都乘以最简公分母 (x+1)(x-1) 得整式方程解这个整式方程得x=1究竟是不是原方程的根?把x=1代入原方程检验x=1使某些分式的分母的值为零也就是使分式 和 没有意义∴ x=1不是原方程的根,原分式方程无解。x=18是原方程的根x(x-6)检验化解x=1不是原方程的根(x+1)(x-1)化解检验(1)为了解分式方程,就要把它化为整式方程; 分式方程的两边乘以同一个含有未知数的整式,这个整式一般取分式方程中各分式的最简公分母。(2)这样得到的整式方程的解有时与原分式方程
的解相同;有时与原分式方程的解不同。分式方程的解法 分式方程 整式方程 去分母思考:
1、如何去分母?
2、解分式方程为什么要验根?怎样验根?怎样进行检验呢?方法一:把整式方程的根代入原方程,看它是否使原分式方程中的分式有意义;方法二:把整式方程的根代入最简公分母,如果最简公分母的值等于0,则产生了增根,如果最简公分母的值不等于0,则原方程没有产生增根。增根 在方程变形时,有时可能产生不适合原方程的根,这种根叫做原方程的增根。 因为解分式方程时可能会产生增根,所以解分式方程必需检验。例1解方程:例2解方程:解题回顾1、在方程的两边都乘以最简公分母,
约去分母,化成整式方程 ;2、解这个整式方程 ;3、把整式方程的根代入最简公分母,看结
果是不是零,使最简公分母为零的根是原
方程的增根,必须舍去。解分式方程的注意点:(1)去分母时,先确定最简公分母;若分母
是多项式,要进行因式分解;
(2)去分母时,不要漏乘不含分母的项;
(3)最后不要忘记验根。1、判断:小结1. 分式方程的概念:2. 可化为一元一次方程的分式方程的解题步骤:分母里含有未知数的方程叫做分式方程。一化二解三检验作业课本第101页第1题,第102页第1题中(1)、(2)小题判断下列解法是否正确:21解答题: 关于x的方程
无解,试求m的值。 它们有区别吗?有联系吗?=去分母:等式基本性质2 通分:分式基本性质
