17.3 可化为一元一次方程的分式方程[下学期]
文档属性
| 名称 | 17.3 可化为一元一次方程的分式方程[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 420.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-19 23:49:00 | ||
图片预览






文档简介
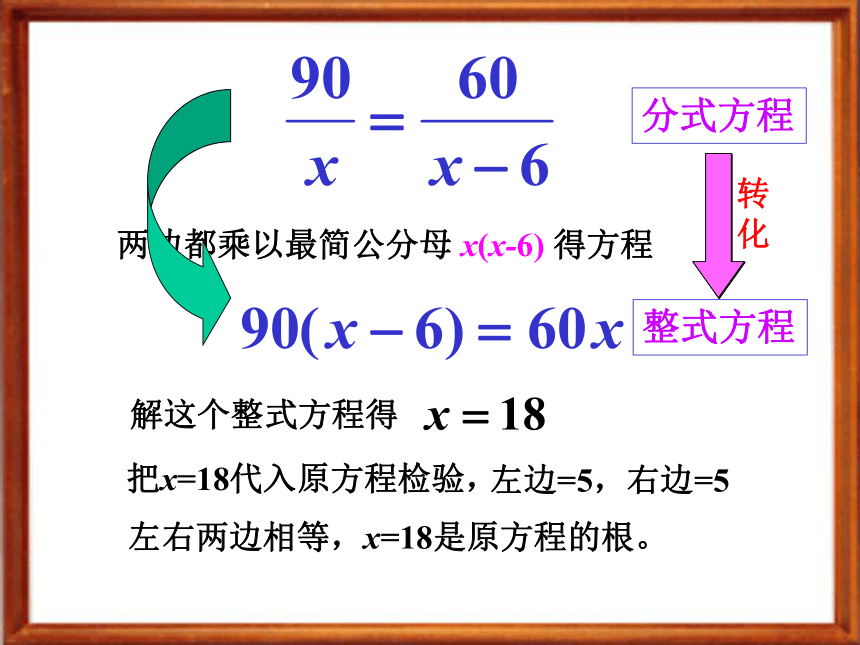
课件17张PPT。 数学世界应该是一个让你感到幸福和快乐的世界,希望你能体会到数学的好,数学给你带来得美!祝同学们学习进步!学有所得!21、4可化为一元一次方程的分式方程甲乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,求甲、乙每小时各做多少个?问题设甲每小时做x个零件,那么乙每小时做(x-6)个。甲做90个所用的时间为:乙做60个所用的时间为:根据题意,列出方程为:新知:分母中含有未知数的方程叫做分式方程练习判断下列说法是否正确:( )( )( )( )否是否是两边都乘以最简公分母 x(x-6) 得方程解这个整式方程得分式方程整式方程转化把x=18代入原方程检验,左边=5,右边=5左右两边相等,x=18是原方程的根。两边都乘以最简公分母 (x+1)(x-1) 得整式方程解这个整式方程得x=1究竟是不是原方程的根?把x=1代入原方程检验x=1使某些分式的分母的值为零∴ x=1不是原方程的根,原分式方程无解。 ⑴在原方程变形时,有时可能产生不适合原方
程的根,这种根叫做原方程的增根。⑵增根是如何产生的?方程两边都乘以(x-3)(x-3)╳ ╳ (x-3)(x-3)╳ ╳ (x-3)增根(x-3)╳ ╳ (x-3)(x-3)╳ ╳ (x-3)怎样进行检验呢?方法一:把整式方程的根代入原分式方程,看它是否能使原分式方程中左右两边的值相等。若相等则是根,反之则是增根,需舍去。方法二:把整式方程的根代入最简公分母,如果最简公分母的值等于0,则产生了增根,如果最简公分母的值不等于0,则原方程没有产生增根。 因为解分式方程时可能会产生增根,所以解分式方程必需检验。x=18是原方程的根x(x-6)检验化解x=1不是原方程的根(x+1)(x-1)化解检验解分式方程的一般步骤1、在方程的两边都乘以最简公分母,
约去分母,化成整式方程 ;2、解这个整式方程 ;3、把整式方程的根代入最简公分母,看结
果是不是零,使最简公分母为零的根是原
方程的增根,必须舍去。注意1.若方程中的分母是多项式,须先分解因式.再确定最简公分母.
2.若方程中的含有整数项,去分母时不要漏乘.课堂练习:
(1)
?
(2)知识拓展2、若关于x的方程
有增根,则增根是 ( )
解:在方程两边都乘以x(x-1)得
3(x-1)+6x=x+m所以8x-m-3=0.因为方程的增根是x=0或x=1所以m= -3或m=5.知识拓展知识拓展知识回顾分式方程步骤转化为整式方程解这个整式方程检验增根
程的根,这种根叫做原方程的增根。⑵增根是如何产生的?方程两边都乘以(x-3)(x-3)╳ ╳ (x-3)(x-3)╳ ╳ (x-3)增根(x-3)╳ ╳ (x-3)(x-3)╳ ╳ (x-3)怎样进行检验呢?方法一:把整式方程的根代入原分式方程,看它是否能使原分式方程中左右两边的值相等。若相等则是根,反之则是增根,需舍去。方法二:把整式方程的根代入最简公分母,如果最简公分母的值等于0,则产生了增根,如果最简公分母的值不等于0,则原方程没有产生增根。 因为解分式方程时可能会产生增根,所以解分式方程必需检验。x=18是原方程的根x(x-6)检验化解x=1不是原方程的根(x+1)(x-1)化解检验解分式方程的一般步骤1、在方程的两边都乘以最简公分母,
约去分母,化成整式方程 ;2、解这个整式方程 ;3、把整式方程的根代入最简公分母,看结
果是不是零,使最简公分母为零的根是原
方程的增根,必须舍去。注意1.若方程中的分母是多项式,须先分解因式.再确定最简公分母.
2.若方程中的含有整数项,去分母时不要漏乘.课堂练习:
(1)
?
(2)知识拓展2、若关于x的方程
有增根,则增根是 ( )
解:在方程两边都乘以x(x-1)得
3(x-1)+6x=x+m所以8x-m-3=0.因为方程的增根是x=0或x=1所以m= -3或m=5.知识拓展知识拓展知识回顾分式方程步骤转化为整式方程解这个整式方程检验增根
