17.3 可化为一元一次方程的分式方程(1)[下学期]
文档属性
| 名称 | 17.3 可化为一元一次方程的分式方程(1)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 354.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-24 00:00:00 | ||
图片预览





文档简介
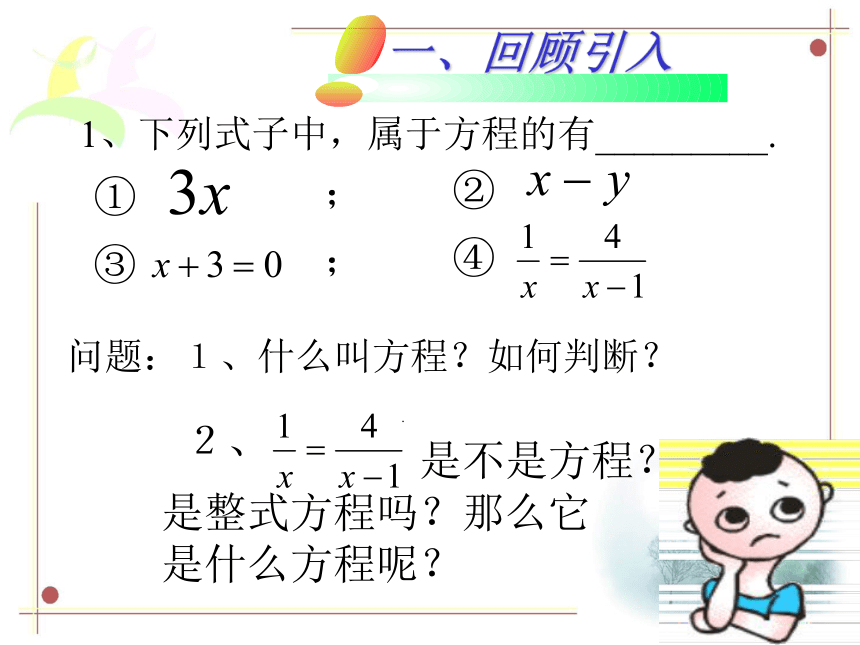
课件19张PPT。17.3 可化为一元一次方程的分式方程1.分式方程的 定义及解法 一、回顾引入1、下列式子中,属于方程的有_________.①; ②③; ④.问题:1、什么叫方程?如何判断? 2、 是不是方程?
是整式方程吗?那么它
是什么方程呢?分式方程的主要特征:
(1)含有分式 ;(2)分母中含有未知数。 方程中 含有分式,并且分母中含有未知数,像这样的方程叫做分式方程.你还能举出一个分式方程的吗?分式方程的概念辨析:判断下列各式哪个是分式方程.(2)(3)(4)(5)(1)练习探究分式方程的解法 1、思 考 : 怎样解分式方程呢?
为了解决本问题,请同学们先思考并回答以下问题:
1)、回顾一下一元一次方程时是怎么去分母的,从中能否得到一点启发?
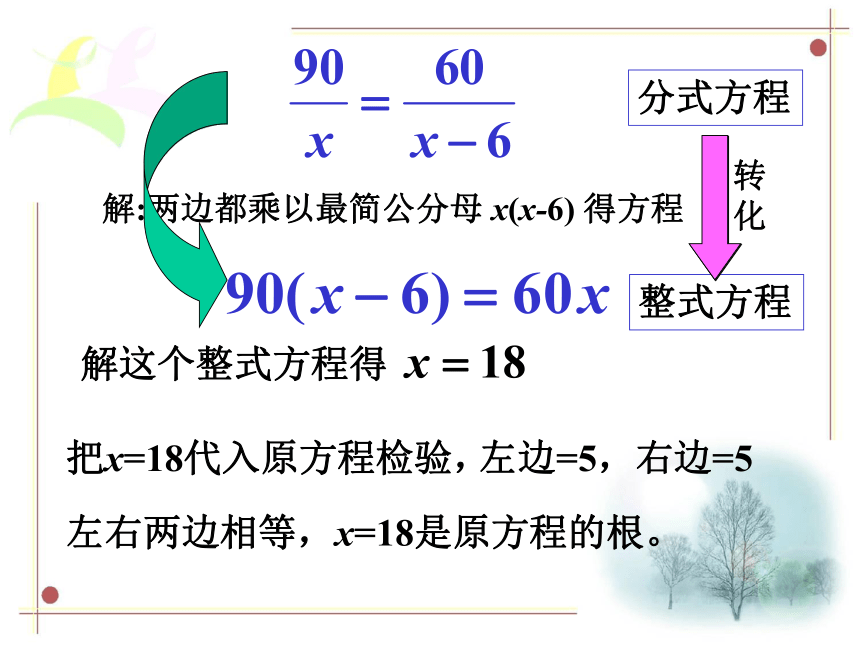
2)有没有办法可以去掉分式方程的分母把它转化为整式方程呢? 解:两边都乘以最简公分母 x(x-6) 得方程解这个整式方程得分式方程整式方程转化把x=18代入原方程检验,左边=5,右边=5左右两边相等,x=18是原方程的根。2、概 括
上述解分式方程的过程,实质上是将方程的两边乘以同一个整式,约去分母,把分式方程转化为整式方程来解.所乘的整式通常取方程中出现的各分式的最简公分母.探究分式方程的解法 解方程:请你动手做一做:例1、解方程:解:两边都乘以最简公分母 (x+1)(x-1) 得整式方程解这个整式方程得x=1究竟是不是原方程的根?当x=1时,原分式方程左边和右边的分母
与 都是0,方程中出现的两个分式都没有意义,∴ x=1不是原方程的根,原分式方程无解。 在将分式方程变形为整式方程时,方程两边同乘以一个含未知数的整式,并约去了分母,有时可能产生不适合原分式方程的解(或根),这种根通常称为增根.探究分式方程的增根原因 因为解分式方程时可能会产生增根,所以解
分式方程必需检验。怎样进行检验呢?方法一:把整式方程的根代入原方程,看它是否使原分式方程中的分式有意义;方法二:把整式方程的根代入最简公分母,如果最简公分母为0,则是原方程的增根,如果最简公分母不为0,则是原方程的根。探究分式方程的验根方法 例2解方程:解题回顾1、在方程的两边都乘以最简公分母,
约去分母,化成整式方程 ;2、解这个整式方程 ;3、把整式方程的根代入最简公分母,看结果是不是零,使最简公分母为零的根是原方程的增根,必须舍去。 解方程: 解: 方程两边同乘以检验:把x=5代入 x-4,
得x-4≠0 ∴x=5是原方程的解. (2)解:方程两边同乘以 检验:把x=2代入 x2-4,
得x2-4=0。 ∴x=2是增根,从而原方程无解。. 注意:分式方程的求根过程不一定是同解变形,所以分式方程一定要验根!注意1.若方程中的分母是多项式,须先分解因式.再确定最简公分母.
2.若方程中的含有整数项,去分母时不要漏乘.知识拓展1、关于x的方程 有
增根,则增根是 ( )
2、若关于x的方程
有增根,则k的值是 ( )
点拨:本题是利用产生增根的原因来解答的;
增根就是使分母为0的未知数的值.练习若 有
增根,则增根可能是 ( )
A、0 B、2 C、0或2 D、1
点拨:本题是利用产生增根的原因来解答的;
增根就是使分母为0的未知数的值.知识小结1、理解分式方程的概念:分母含有未知数
2、解分式方程的步骤:⑴去分母;⑵解整式方程;⑶验根;⑷下结论.
3、增根:就是使分母为0的未知数的值,增根应舍去。:一化整二解整三检验思想方法:将分式方程转化为整式方程; 注意事项解分式方程关键的两步:去分母和验根.
特别是千万别忘了要验根,这是与解整
式方程不同的地方。 作业:
P16: 习题1再见
是整式方程吗?那么它
是什么方程呢?分式方程的主要特征:
(1)含有分式 ;(2)分母中含有未知数。 方程中 含有分式,并且分母中含有未知数,像这样的方程叫做分式方程.你还能举出一个分式方程的吗?分式方程的概念辨析:判断下列各式哪个是分式方程.(2)(3)(4)(5)(1)练习探究分式方程的解法 1、思 考 : 怎样解分式方程呢?
为了解决本问题,请同学们先思考并回答以下问题:
1)、回顾一下一元一次方程时是怎么去分母的,从中能否得到一点启发?
2)有没有办法可以去掉分式方程的分母把它转化为整式方程呢? 解:两边都乘以最简公分母 x(x-6) 得方程解这个整式方程得分式方程整式方程转化把x=18代入原方程检验,左边=5,右边=5左右两边相等,x=18是原方程的根。2、概 括
上述解分式方程的过程,实质上是将方程的两边乘以同一个整式,约去分母,把分式方程转化为整式方程来解.所乘的整式通常取方程中出现的各分式的最简公分母.探究分式方程的解法 解方程:请你动手做一做:例1、解方程:解:两边都乘以最简公分母 (x+1)(x-1) 得整式方程解这个整式方程得x=1究竟是不是原方程的根?当x=1时,原分式方程左边和右边的分母
与 都是0,方程中出现的两个分式都没有意义,∴ x=1不是原方程的根,原分式方程无解。 在将分式方程变形为整式方程时,方程两边同乘以一个含未知数的整式,并约去了分母,有时可能产生不适合原分式方程的解(或根),这种根通常称为增根.探究分式方程的增根原因 因为解分式方程时可能会产生增根,所以解
分式方程必需检验。怎样进行检验呢?方法一:把整式方程的根代入原方程,看它是否使原分式方程中的分式有意义;方法二:把整式方程的根代入最简公分母,如果最简公分母为0,则是原方程的增根,如果最简公分母不为0,则是原方程的根。探究分式方程的验根方法 例2解方程:解题回顾1、在方程的两边都乘以最简公分母,
约去分母,化成整式方程 ;2、解这个整式方程 ;3、把整式方程的根代入最简公分母,看结果是不是零,使最简公分母为零的根是原方程的增根,必须舍去。 解方程: 解: 方程两边同乘以检验:把x=5代入 x-4,
得x-4≠0 ∴x=5是原方程的解. (2)解:方程两边同乘以 检验:把x=2代入 x2-4,
得x2-4=0。 ∴x=2是增根,从而原方程无解。. 注意:分式方程的求根过程不一定是同解变形,所以分式方程一定要验根!注意1.若方程中的分母是多项式,须先分解因式.再确定最简公分母.
2.若方程中的含有整数项,去分母时不要漏乘.知识拓展1、关于x的方程 有
增根,则增根是 ( )
2、若关于x的方程
有增根,则k的值是 ( )
点拨:本题是利用产生增根的原因来解答的;
增根就是使分母为0的未知数的值.练习若 有
增根,则增根可能是 ( )
A、0 B、2 C、0或2 D、1
点拨:本题是利用产生增根的原因来解答的;
增根就是使分母为0的未知数的值.知识小结1、理解分式方程的概念:分母含有未知数
2、解分式方程的步骤:⑴去分母;⑵解整式方程;⑶验根;⑷下结论.
3、增根:就是使分母为0的未知数的值,增根应舍去。:一化整二解整三检验思想方法:将分式方程转化为整式方程; 注意事项解分式方程关键的两步:去分母和验根.
特别是千万别忘了要验根,这是与解整
式方程不同的地方。 作业:
P16: 习题1再见
