18.1.1 平行四边形的性质 同步练习题(含答案)
文档属性
| 名称 | 18.1.1 平行四边形的性质 同步练习题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 489.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 11:18:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级数学下册第18章《18.1.1平行四边形的性质》
同步练习题(含答案)
一、单选题
1.平行四边形中,若,则的度数为( )
A.30° B.60 C.120° D.150°
2.已知的周长为56,,则的长为( )
A.18 B.23 C.36 D.46
3.如图,在□ABCD中,AB=10,AD=8,AC⊥BC,则□ABCD的面积为( )
A.80 B.60 C.48 D.40
4.如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A.4s B.3s C.2s D.1s
5.如图,△ABC的面积为16,点D是BC边上一点,且BD=BC,点G是AB边上一点,点H在△ABC内部,BD∥GH,且BD=GH.则图中阴影部分的面积是( )
A.3 B.4 C.5 D.6
6.如图,四边形ACED为平行四边形,DF垂直平分BE,甲、乙两虫同时从A点开始爬行到点F,甲虫沿着A-D-E-F的路线爬行,乙虫沿着A-C-B-F的路线爬行,若它们的爬行速度相同,则( )
A.甲虫先到 B.乙虫先到
C.两虫同时到 D.无法确定
7.如图,□ABCD中,∠C=100°,BE平分∠ABC,则∠AEB的度数为( )
A.60° B.50° C.40° D.30°
8.如图,已知 ABCD的周长为20,∠ADC的平分线DE交AB于点E,若AD=4,则BE的长为( )
A.1 B.1.5 C.2 D.3
9.如图平行四边形ABCD的面积为24,E为AB上的中点,连接CE、DE,DE、AC的交点为O,则三角形OCE的面积为( )
A.2 B.3 C.4 D.6
10.如图,点P是 ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是、、、,给出如下结论:①;②如果,则;③若,则;④若,则P点一定在对角线BD上.其中正确的有( )
A.①③ B.②④ C.②③ D.①④
二、填空题
11.如图,中两个邻角的度数比为1:3,则其中较小的内角的度数为 _______.
12.平行四边形两邻边分别是4和6,其中一边上的高是3,则平行四边形的面积是______.
13.在平行四边形ABCD中,点P是BC边上任意一点,连结PA,PD,若平行四边形ABCD的面积为12.8,则△PAD的面积为_____.
14.如图,在 ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4,则CE的长是___.
15.在平行四边形ABCD中,∠B+∠D=190°,则∠A=_____°.
三、解答题
16.如图所示,ABCD中,AE⊥BD,,垂足分别为E,F.求证:AE=CF.
17.如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数
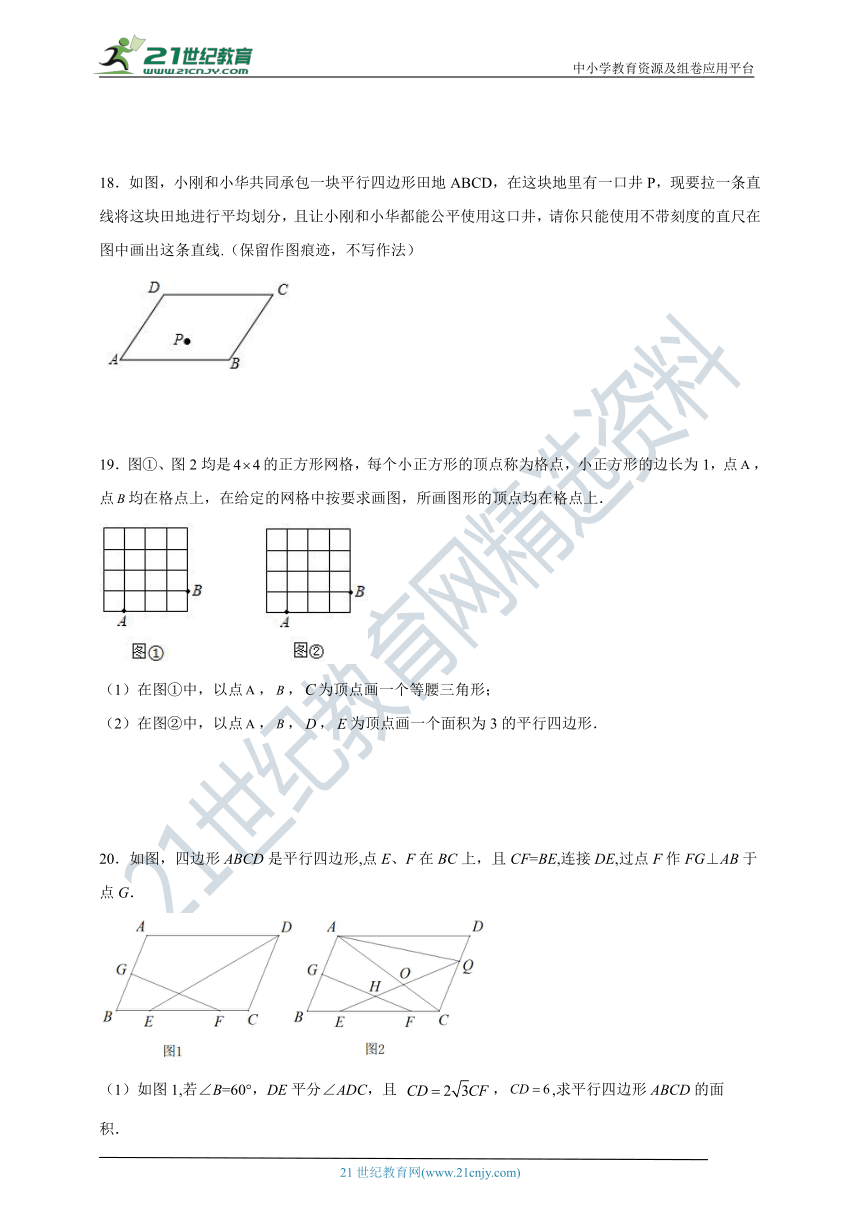
18.如图,小刚和小华共同承包一块平行四边形田地ABCD,在这块地里有一口井P,现要拉一条直线将这块田地进行平均划分,且让小刚和小华都能公平使用这口井,请你只能使用不带刻度的直尺在图中画出这条直线.(保留作图痕迹,不写作法)
19.图①、图2均是的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点,点均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
(1)在图①中,以点,,为顶点画一个等腰三角形;
(2)在图②中,以点,,,为顶点画一个面积为3的平行四边形.
20.如图,四边形ABCD是平行四边形,点E、F在BC上,且CF=BE,连接DE,过点F作FG⊥AB于点G.
(1)如图1,若∠B=60°,DE平分∠ADC,且 ,,求平行四边形ABCD的面积.
(2)点H在GF上,且HE=HF,延长EH交AC,CD于点O,Q,连接AQ,若AC=BC=EQ,∠EQC=45°,求证: .
参考答案
1.C2.A3.C4.B5.B6.C7.C8.C9.C10.D
11.45°
12.12或18##18或12
13.6.4
14.
15.85
16.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF.
17.(1)∵四边形ABCD是平行四边形,
∴ ,
∴∠ADE=∠DEC,
又∵DE平分∠ADC,
∴∠ADE=∠EDC,
∴∠DEC=∠EDC,
∴CD=CE;
(2)∵四边形ABCD是平行四边形,
∴,AB=CD,
∴∠B+∠BAD=180°,
又∵∠B=80°,
∴∠BAD=180°-80°=100°,
∵BE=CE,CE=CD,
∴AB=BE,
∴∠BAE=∠BEA=(180°-80°)÷2=50°,
∴∠DAE=∠BAD-∠BAE=100°-50°=50°.
18.连接AC、BD相交于O点,连接OP与AD相交于E点,于BC相交于F点,一人分得四边形AEFB,一人分得四边形EDCF
19.解:(1)如图①中,此时以为顶点,为底边,该即为所求(答案不唯一).
(2)如图②中,此时底,高,因此四边形即为所求.
20.(1)∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠CED,
∴∠CED=∠CDE,
∴CD=CE=6,
∵,
∴CF=,
∵CF=BE,
∴BE=,
∴BC=6+.
过点A作AM⊥BC于点M,
∵∠B=60°,AB=CD=6,
∴∠BAM=30°,
∴BM=3,
∴AM=BM=,
∴平行四边形ABCD的面积=(6+)×=18+9;
(2)过点C作CN⊥EQ于点N,其延长线交AD于点K,
∵∠EQC=45°,
∴△CNQ为等腰直角三角形,
∴∠NQC=∠NCQ=45°,且CQ=CN,
∵HE=HF,
∴∠HEF=∠HFE,
∵FG⊥AB,CN⊥EQ,
∴∠FGB=∠ENC=90°,
又∵BE=CF,
∴BF=CE,
∴△BGF≌△CNE(AAS),
∴BG=CN,∠B=∠ECN,
∴CQ=BG,
又∵AC=BC=AD,
∴∠D=∠ACD,
又∵∠B=∠D,
∴∠ECN=∠ACD,
∴∠KAC=∠BCA=∠NCQ=45°,
∴∠BAC=∠ACD=∠B=∠CDA=∠ECN =67.5°,
∴∠ACK= ∠ECN-∠BCA =22.5°,∠QEC=180°-90°-∠ECN =22.5°,
即:∠ACK=∠QEC,
又∵∠KAC=∠CQE=45°,AC=QE,
∴△ACK≌△QEC(ASA),
∴CK=CE,
∵∠CDA=67.5°,∠NCQ=45°,
∴∠CKD=180°-45°-67.5°=67.5°,
∴∠CKD=∠CDA,
∴CK=CD,
∴CE=CD,
∵CD=CQ+QD=BG+DQ,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学下册第18章《18.1.1平行四边形的性质》
同步练习题(含答案)
一、单选题
1.平行四边形中,若,则的度数为( )
A.30° B.60 C.120° D.150°
2.已知的周长为56,,则的长为( )
A.18 B.23 C.36 D.46
3.如图,在□ABCD中,AB=10,AD=8,AC⊥BC,则□ABCD的面积为( )
A.80 B.60 C.48 D.40
4.如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A.4s B.3s C.2s D.1s
5.如图,△ABC的面积为16,点D是BC边上一点,且BD=BC,点G是AB边上一点,点H在△ABC内部,BD∥GH,且BD=GH.则图中阴影部分的面积是( )
A.3 B.4 C.5 D.6
6.如图,四边形ACED为平行四边形,DF垂直平分BE,甲、乙两虫同时从A点开始爬行到点F,甲虫沿着A-D-E-F的路线爬行,乙虫沿着A-C-B-F的路线爬行,若它们的爬行速度相同,则( )
A.甲虫先到 B.乙虫先到
C.两虫同时到 D.无法确定
7.如图,□ABCD中,∠C=100°,BE平分∠ABC,则∠AEB的度数为( )
A.60° B.50° C.40° D.30°
8.如图,已知 ABCD的周长为20,∠ADC的平分线DE交AB于点E,若AD=4,则BE的长为( )
A.1 B.1.5 C.2 D.3
9.如图平行四边形ABCD的面积为24,E为AB上的中点,连接CE、DE,DE、AC的交点为O,则三角形OCE的面积为( )
A.2 B.3 C.4 D.6
10.如图,点P是 ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是、、、,给出如下结论:①;②如果,则;③若,则;④若,则P点一定在对角线BD上.其中正确的有( )
A.①③ B.②④ C.②③ D.①④
二、填空题
11.如图,中两个邻角的度数比为1:3,则其中较小的内角的度数为 _______.
12.平行四边形两邻边分别是4和6,其中一边上的高是3,则平行四边形的面积是______.
13.在平行四边形ABCD中,点P是BC边上任意一点,连结PA,PD,若平行四边形ABCD的面积为12.8,则△PAD的面积为_____.
14.如图,在 ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4,则CE的长是___.
15.在平行四边形ABCD中,∠B+∠D=190°,则∠A=_____°.
三、解答题
16.如图所示,ABCD中,AE⊥BD,,垂足分别为E,F.求证:AE=CF.
17.如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数
18.如图,小刚和小华共同承包一块平行四边形田地ABCD,在这块地里有一口井P,现要拉一条直线将这块田地进行平均划分,且让小刚和小华都能公平使用这口井,请你只能使用不带刻度的直尺在图中画出这条直线.(保留作图痕迹,不写作法)
19.图①、图2均是的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点,点均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
(1)在图①中,以点,,为顶点画一个等腰三角形;
(2)在图②中,以点,,,为顶点画一个面积为3的平行四边形.
20.如图,四边形ABCD是平行四边形,点E、F在BC上,且CF=BE,连接DE,过点F作FG⊥AB于点G.
(1)如图1,若∠B=60°,DE平分∠ADC,且 ,,求平行四边形ABCD的面积.
(2)点H在GF上,且HE=HF,延长EH交AC,CD于点O,Q,连接AQ,若AC=BC=EQ,∠EQC=45°,求证: .
参考答案
1.C2.A3.C4.B5.B6.C7.C8.C9.C10.D
11.45°
12.12或18##18或12
13.6.4
14.
15.85
16.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF.
17.(1)∵四边形ABCD是平行四边形,
∴ ,
∴∠ADE=∠DEC,
又∵DE平分∠ADC,
∴∠ADE=∠EDC,
∴∠DEC=∠EDC,
∴CD=CE;
(2)∵四边形ABCD是平行四边形,
∴,AB=CD,
∴∠B+∠BAD=180°,
又∵∠B=80°,
∴∠BAD=180°-80°=100°,
∵BE=CE,CE=CD,
∴AB=BE,
∴∠BAE=∠BEA=(180°-80°)÷2=50°,
∴∠DAE=∠BAD-∠BAE=100°-50°=50°.
18.连接AC、BD相交于O点,连接OP与AD相交于E点,于BC相交于F点,一人分得四边形AEFB,一人分得四边形EDCF
19.解:(1)如图①中,此时以为顶点,为底边,该即为所求(答案不唯一).
(2)如图②中,此时底,高,因此四边形即为所求.
20.(1)∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠CED,
∴∠CED=∠CDE,
∴CD=CE=6,
∵,
∴CF=,
∵CF=BE,
∴BE=,
∴BC=6+.
过点A作AM⊥BC于点M,
∵∠B=60°,AB=CD=6,
∴∠BAM=30°,
∴BM=3,
∴AM=BM=,
∴平行四边形ABCD的面积=(6+)×=18+9;
(2)过点C作CN⊥EQ于点N,其延长线交AD于点K,
∵∠EQC=45°,
∴△CNQ为等腰直角三角形,
∴∠NQC=∠NCQ=45°,且CQ=CN,
∵HE=HF,
∴∠HEF=∠HFE,
∵FG⊥AB,CN⊥EQ,
∴∠FGB=∠ENC=90°,
又∵BE=CF,
∴BF=CE,
∴△BGF≌△CNE(AAS),
∴BG=CN,∠B=∠ECN,
∴CQ=BG,
又∵AC=BC=AD,
∴∠D=∠ACD,
又∵∠B=∠D,
∴∠ECN=∠ACD,
∴∠KAC=∠BCA=∠NCQ=45°,
∴∠BAC=∠ACD=∠B=∠CDA=∠ECN =67.5°,
∴∠ACK= ∠ECN-∠BCA =22.5°,∠QEC=180°-90°-∠ECN =22.5°,
即:∠ACK=∠QEC,
又∵∠KAC=∠CQE=45°,AC=QE,
∴△ACK≌△QEC(ASA),
∴CK=CE,
∵∠CDA=67.5°,∠NCQ=45°,
∴∠CKD=180°-45°-67.5°=67.5°,
∴∠CKD=∠CDA,
∴CK=CD,
∴CE=CD,
∵CD=CQ+QD=BG+DQ,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
