江苏省苏州市太仓市2022-2023学年八年级下学期 第六周滚动练习(无答案)
文档属性
| 名称 | 江苏省苏州市太仓市2022-2023学年八年级下学期 第六周滚动练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 126.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-21 17:10:55 | ||
图片预览

文档简介
2022-2023学年八年级(下)期末数学第六周滚动练习
一、选择题:(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确选项前的字母代号填写在答题卷相应位置上.)
1.(3分)下列图形中,既是中心对称图形又是轴对称图形的是( )
A.B.C.D.
2.(3分)下列调查方式中适合的是( )
A.要了解一批节能灯的使用寿命,采用普查方式
B.调查你所在班级同学的身高,采用抽样调查方式
C.环保部门调查沱江某段水域的水质情况,采用抽样调查方式
D.调查全市中学生每天的就寝时间,采用普查方式
3.(3分)从一副扑克牌中任意抽取1张,下列事件发生的可能性最大的是( )
A.这张牌是“A” B.这张牌是“大王”
C.这张牌是“黑桃” D.这张牌的点数是10
4.(3分)若分式的值为零,则( )A.x=3 B.x=﹣3 C.x=2 D.x=﹣2
5.(3分)一个不透明的袋子中装有2个红球、3个白球,每个球除颜色外都相同.从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是红球 B.至少有1个球是白球
C.至少有2个球是红球 D.至少有2个球是白球
6.(3分)如图,菱形ABCD中,对角线AC、BD相交于点O,若BD=AD=4,则AC的长为( )
A.6 B.8 C. D.
第6题第8题
7.(3分)若点A(﹣2,y1)、B(﹣1,y2)、C(1,y3)都在反比例函数(k为常数)的图象上,则y1、y2、y3的大小关系为( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y1<y3 D.y3<y2<y1
8.(3分)如图,在 ABCD中,BE垂直平分CD于点E,∠BAD=45°,AD=6,则 ABCD的对角线AC的长为( )A.6 B.4 C.10 D.10
第9题第10题
9.(3分)如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF=( )A. B. C.1 D.
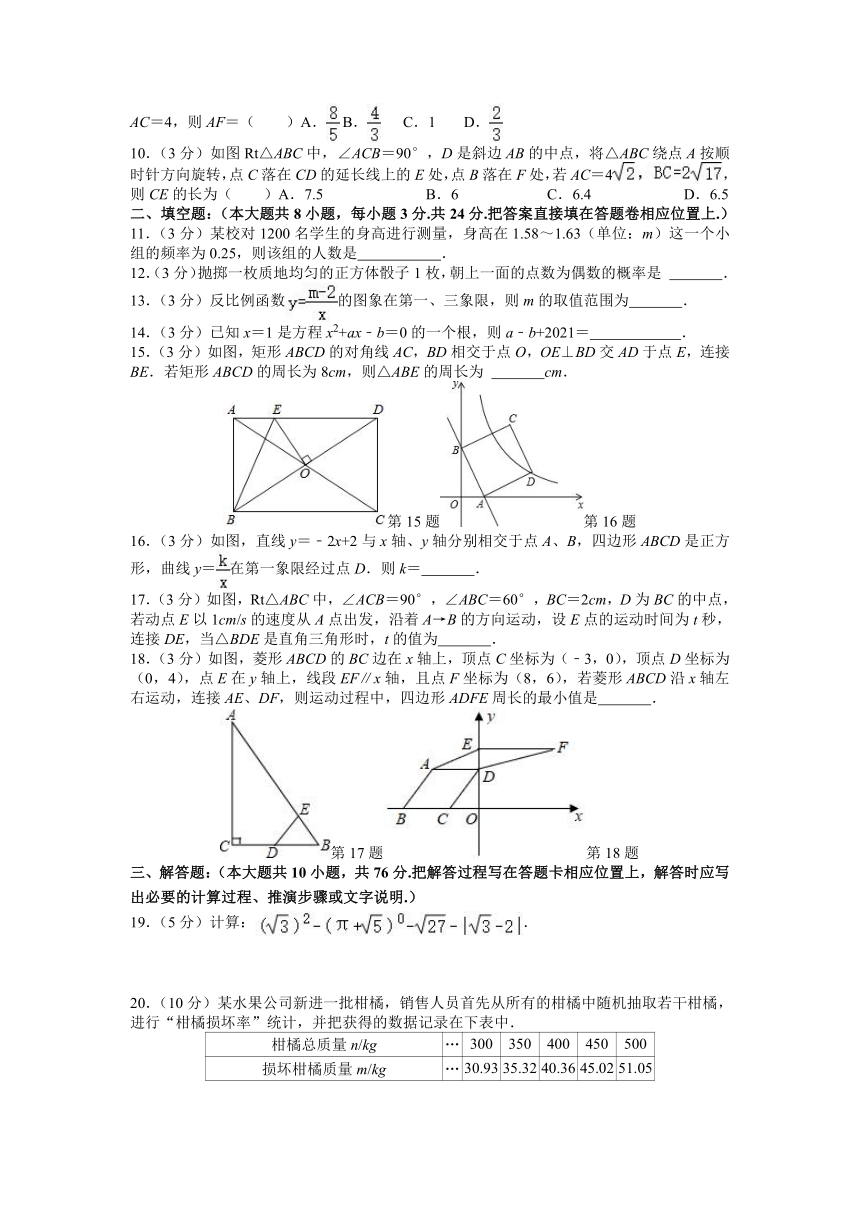
10.(3分)如图Rt△ABC中,∠ACB=90°,D是斜边AB的中点,将△ABC绕点A按顺时针方向旋转,点C落在CD的延长线上的E处,点B落在F处,若AC=4,则CE的长为( )A.7.5 B.6 C.6.4 D.6.5
二、填空题:(本大题共8小题,每小题3分.共24分.把答案直接填在答题卷相应位置上.)
11.(3分)某校对1200名学生的身高进行测量,身高在1.58~1.63(单位:m)这一个小组的频率为0.25,则该组的人数是 .
12.(3分)抛掷一枚质地均匀的正方体骰子1枚,朝上一面的点数为偶数的概率是 .
13.(3分)反比例函数的图象在第一、三象限,则m的取值范围为 .
14.(3分)已知x=1是方程x2+ax﹣b=0的一个根,则a﹣b+2021= .
15.(3分)如图,矩形ABCD的对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若矩形ABCD的周长为8cm,则△ABE的周长为 cm.
第15题第16题
16.(3分)如图,直线y=﹣2x+2与x轴、y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=在第一象限经过点D.则k= .
17.(3分)如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为 .
18.(3分)如图,菱形ABCD的BC边在x轴上,顶点C坐标为(﹣3,0),顶点D坐标为(0,4),点E在y轴上,线段EF∥x轴,且点F坐标为(8,6),若菱形ABCD沿x轴左右运动,连接AE、DF,则运动过程中,四边形ADFE周长的最小值是 .
第17题第18题
三、解答题:(本大题共10小题,共76分.把解答过程写在答题卡相应位置上,解答时应写出必要的计算过程、推演步骤或文字说明.)
19.(5分)计算:.
20.(10分)某水果公司新进一批柑橘,销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在下表中.
柑橘总质量n/kg … 300 350 400 450 500
损坏柑橘质量m/kg … 30.93 35.32 40.36 45.02 51.05
柑橘损坏的频率(精确到0.001) … 0.103 0.101 a 0.100 b
(1)填空:a≈ ,b≈ ;
(2)柑橘完好的概率约为 (精确到0.1);
(3)柑橘的总重量为10000kg,成本价是1.8元/kg,公司希望这些柑橘能够获得利润5400元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
21.(5分)化简并求值:,其中a=.
22.(6分)“生活垃圾分类”逐渐成为社会生活新风尚,某学校为了了解学生对“生活垃圾分类”的看法,随机调查了200名学生(每名学生必须选择且只能选择一类看法),调查结果分为“A.很有必要”“B.有必要”“C.无所谓”“D.没有必要”四类.并根据调查结果绘制了图1和图2两幅统计图(均不完整),请根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)扇形统计图中“D.没有必要”所在扇形的圆心角度数为 ;
(3)该校共有2500名学生,根据调查结果估计该校对“生活垃圾分类”认为“A.很有必要”的学生人数.
23.(7分)已知反比例函数y=(m为常数,且m≠3)
(1)若在其图象的每一个分支上,y随x增大而减小,求m的取值范围;
(2)若点A(2,)在该反比例函数的图象上;
①求m的值;
②当x<﹣1时,请写出y的取值范围.
24.(7分)如图,在△ABC中,∠BAC=50°,将△ABC绕点A按逆时针方向旋转后得△AB1C1.当B1B∥AC时,求∠BAC1的度数.
25.(8分)为了改善生态环境,防止水土流失,某村计划在荒坡上种树1080棵.由于青年志愿者支援,实际每天种树的棵数比原计划每天多50%,结果提前6天完成任务.原计划每天种树多少棵?
26.(8分)如图,点E、F分别在 ABCD的边AB、CD的延长线上,且BE=DF,连接AC、EF、AF、CE,AC与EF交于点O.
(1)求证:AC、EF互相平分;
(2)若EF平分∠AEC,求证:四边形AECF是菱形.
27.(10分)【了解概念】
将平面直角坐标系中过某一定点且不与x轴垂直的直线,叫该定点的“友好线”.若点P(1,0),则点P的“友好线”可记为y=k(x﹣1).
【理解运用】
(1)已知点A的“友好线”可记为y=kx﹣3k+,则点A的坐标为 ;
(2)若点B(3,2)的“友好线”恰好经过点(1,1),求该“友好线”的解析式;
【拓展提升】
(3)已知点M在点Q的“友好线”y=k(x+2)﹣1上,点N在直线y=﹣x+2上,若M(a,m),N(a,n),且当﹣3≤a≤3时,m≤n,请直接确定k的取值范围.
28.(10分)如图,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点B坐标为(4,﹣3).把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E.
(1)线段AC= ;
(2)求点D坐标及折痕DE的长;
(3)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请求出点Q的坐标;若不存在,请说明理由.
一、选择题:(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确选项前的字母代号填写在答题卷相应位置上.)
1.(3分)下列图形中,既是中心对称图形又是轴对称图形的是( )
A.B.C.D.
2.(3分)下列调查方式中适合的是( )
A.要了解一批节能灯的使用寿命,采用普查方式
B.调查你所在班级同学的身高,采用抽样调查方式
C.环保部门调查沱江某段水域的水质情况,采用抽样调查方式
D.调查全市中学生每天的就寝时间,采用普查方式
3.(3分)从一副扑克牌中任意抽取1张,下列事件发生的可能性最大的是( )
A.这张牌是“A” B.这张牌是“大王”
C.这张牌是“黑桃” D.这张牌的点数是10
4.(3分)若分式的值为零,则( )A.x=3 B.x=﹣3 C.x=2 D.x=﹣2
5.(3分)一个不透明的袋子中装有2个红球、3个白球,每个球除颜色外都相同.从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是红球 B.至少有1个球是白球
C.至少有2个球是红球 D.至少有2个球是白球
6.(3分)如图,菱形ABCD中,对角线AC、BD相交于点O,若BD=AD=4,则AC的长为( )
A.6 B.8 C. D.
第6题第8题
7.(3分)若点A(﹣2,y1)、B(﹣1,y2)、C(1,y3)都在反比例函数(k为常数)的图象上,则y1、y2、y3的大小关系为( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y1<y3 D.y3<y2<y1
8.(3分)如图,在 ABCD中,BE垂直平分CD于点E,∠BAD=45°,AD=6,则 ABCD的对角线AC的长为( )A.6 B.4 C.10 D.10
第9题第10题
9.(3分)如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF=( )A. B. C.1 D.
10.(3分)如图Rt△ABC中,∠ACB=90°,D是斜边AB的中点,将△ABC绕点A按顺时针方向旋转,点C落在CD的延长线上的E处,点B落在F处,若AC=4,则CE的长为( )A.7.5 B.6 C.6.4 D.6.5
二、填空题:(本大题共8小题,每小题3分.共24分.把答案直接填在答题卷相应位置上.)
11.(3分)某校对1200名学生的身高进行测量,身高在1.58~1.63(单位:m)这一个小组的频率为0.25,则该组的人数是 .
12.(3分)抛掷一枚质地均匀的正方体骰子1枚,朝上一面的点数为偶数的概率是 .
13.(3分)反比例函数的图象在第一、三象限,则m的取值范围为 .
14.(3分)已知x=1是方程x2+ax﹣b=0的一个根,则a﹣b+2021= .
15.(3分)如图,矩形ABCD的对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若矩形ABCD的周长为8cm,则△ABE的周长为 cm.
第15题第16题
16.(3分)如图,直线y=﹣2x+2与x轴、y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=在第一象限经过点D.则k= .
17.(3分)如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为 .
18.(3分)如图,菱形ABCD的BC边在x轴上,顶点C坐标为(﹣3,0),顶点D坐标为(0,4),点E在y轴上,线段EF∥x轴,且点F坐标为(8,6),若菱形ABCD沿x轴左右运动,连接AE、DF,则运动过程中,四边形ADFE周长的最小值是 .
第17题第18题
三、解答题:(本大题共10小题,共76分.把解答过程写在答题卡相应位置上,解答时应写出必要的计算过程、推演步骤或文字说明.)
19.(5分)计算:.
20.(10分)某水果公司新进一批柑橘,销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在下表中.
柑橘总质量n/kg … 300 350 400 450 500
损坏柑橘质量m/kg … 30.93 35.32 40.36 45.02 51.05
柑橘损坏的频率(精确到0.001) … 0.103 0.101 a 0.100 b
(1)填空:a≈ ,b≈ ;
(2)柑橘完好的概率约为 (精确到0.1);
(3)柑橘的总重量为10000kg,成本价是1.8元/kg,公司希望这些柑橘能够获得利润5400元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
21.(5分)化简并求值:,其中a=.
22.(6分)“生活垃圾分类”逐渐成为社会生活新风尚,某学校为了了解学生对“生活垃圾分类”的看法,随机调查了200名学生(每名学生必须选择且只能选择一类看法),调查结果分为“A.很有必要”“B.有必要”“C.无所谓”“D.没有必要”四类.并根据调查结果绘制了图1和图2两幅统计图(均不完整),请根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)扇形统计图中“D.没有必要”所在扇形的圆心角度数为 ;
(3)该校共有2500名学生,根据调查结果估计该校对“生活垃圾分类”认为“A.很有必要”的学生人数.
23.(7分)已知反比例函数y=(m为常数,且m≠3)
(1)若在其图象的每一个分支上,y随x增大而减小,求m的取值范围;
(2)若点A(2,)在该反比例函数的图象上;
①求m的值;
②当x<﹣1时,请写出y的取值范围.
24.(7分)如图,在△ABC中,∠BAC=50°,将△ABC绕点A按逆时针方向旋转后得△AB1C1.当B1B∥AC时,求∠BAC1的度数.
25.(8分)为了改善生态环境,防止水土流失,某村计划在荒坡上种树1080棵.由于青年志愿者支援,实际每天种树的棵数比原计划每天多50%,结果提前6天完成任务.原计划每天种树多少棵?
26.(8分)如图,点E、F分别在 ABCD的边AB、CD的延长线上,且BE=DF,连接AC、EF、AF、CE,AC与EF交于点O.
(1)求证:AC、EF互相平分;
(2)若EF平分∠AEC,求证:四边形AECF是菱形.
27.(10分)【了解概念】
将平面直角坐标系中过某一定点且不与x轴垂直的直线,叫该定点的“友好线”.若点P(1,0),则点P的“友好线”可记为y=k(x﹣1).
【理解运用】
(1)已知点A的“友好线”可记为y=kx﹣3k+,则点A的坐标为 ;
(2)若点B(3,2)的“友好线”恰好经过点(1,1),求该“友好线”的解析式;
【拓展提升】
(3)已知点M在点Q的“友好线”y=k(x+2)﹣1上,点N在直线y=﹣x+2上,若M(a,m),N(a,n),且当﹣3≤a≤3时,m≤n,请直接确定k的取值范围.
28.(10分)如图,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点B坐标为(4,﹣3).把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E.
(1)线段AC= ;
(2)求点D坐标及折痕DE的长;
(3)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请求出点Q的坐标;若不存在,请说明理由.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
