函数及其图象复习[下学期]
图片预览





文档简介
课件14张PPT。函数与图象复习1.一次函数 (y = kx+b,k≠0)
(1)k、b的符号对图象的影响是怎样的?
(2)如何求一次函数的图象与坐标轴的交点坐标?
(3)如何画一次函数的图象?
(4)若两条直线互相平行,k的值是否会相同?
(5)会用待定系数法求一次函数的解析式吗?
(6)一次函数的性质如何表述?回顾与思考2.反比例函数 (k≠0) (1)k的符号对图象的影响是怎样的? (2)如何画反比例函数的图象?画图象时与上述
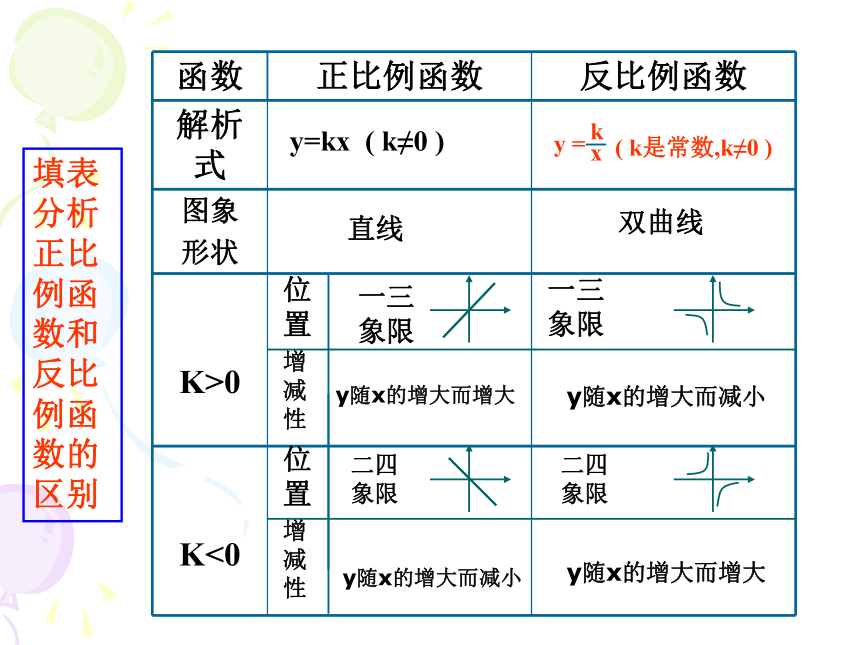
的一次函数的图象的画法有何区别?(3)双曲线经过一点,能确定它的解析式吗? (4)反比例函数的性质是如何描述的?位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限 y随x的增大而减小二四象限二四象限 y随x的增大而减小 y随x的增大而增大
填表分析正比例函数和反比例函数的区别例1 反比例函数的图象经过点A(2,3).
求这个函数的关系式.
请判断点B(1,6)是否在这个反比例函数的图象上.并说明理由.分析求函数的关系式,一般先设出关系式,再用待定系数法求出未
知数k.由题意知反比例函数的图象经过点A(2,3),也就是说点
A(2,3)在图象上,因此它的坐标满足函数的关系式,即当x=2时,
y=3,反过来也是如此,即一个点的坐标如果满足函数的关系式,
就是说这点在图象上.或者说函数的图象经过这个点.解: ①设 由题意有 , 则k=6,
所以这个函数的关系式为②点B(1,6)是否在这个反比例函数的图象上.因为当x=1时,
所以B(1,6)在这个反比例函数的图象上.
例题
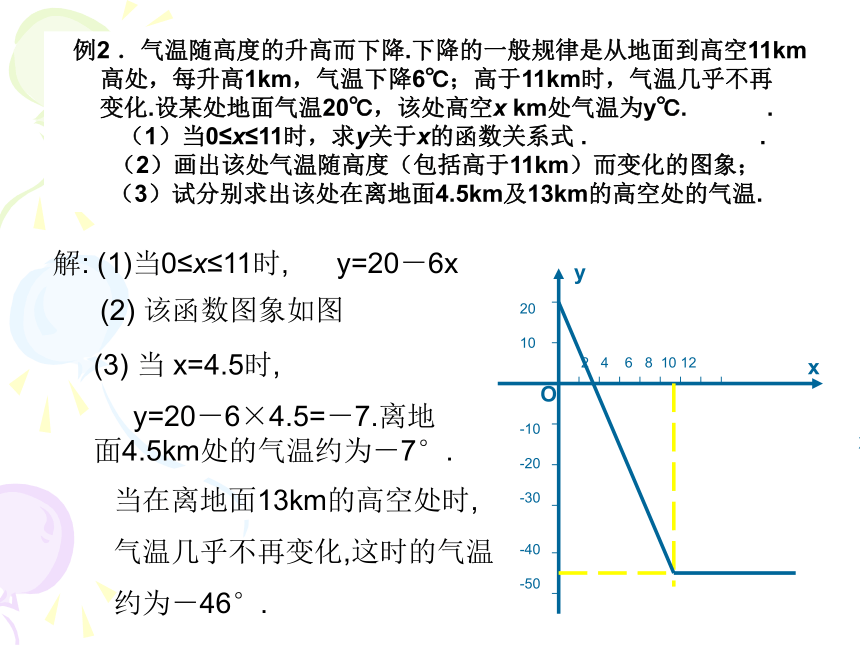
讲解 例2 .气温随高度的升高而下降.下降的一般规律是从地面到高空11km
高处,每升高1km,气温下降6℃;高于11km时,气温几乎不再
变化.设某处地面气温20℃,该处高空x km处气温为y℃. .
(1)当0≤x≤11时,求y关于x的函数关系式 . .
(2)画出该处气温随高度(包括高于11km)而变化的图象;
(3)试分别求出该处在离地面4.5km及13km的高空处的气温.解: (1)当0≤x≤11时, y=20-6x(2) 该函数图象如图(3) 当 x=4.5时,
y=20-6×4.5=-7.离地面4.5km处的气温约为-7°.当在离地面13km的高空处时,
气温几乎不再变化,这时的气温
约为-46°.xyx 1. 如果点A(-3,a)与点B(3,4)关于y轴对称,
那么a的值为( )
A.3 B.-3 C.4 D.-4一 选择题AC3。 某厂今年前五个月生产某种产品的月产量Q(件)关于时间
t (月)的函数图象如图所示,则对这种产品来说,下列说法正确
的是( ).
A。1月至3月每月产量逐月增加,
4、5两月每月产量逐月减少
B. 1月至3月每月产量逐月增加,
4、5两月每月产量与3月持平
C. 1月至3月每月产量逐月增加,
4、5两个月停止生产
D. 1月至3月每月产量不变,
4、5两月停止生产B4.如图,温度计上表示了摄氏温度(℃)与华氏温度(℉)的刻度.
能否用一个函数关系式来表示摄氏温度y(℃)和华氏温度x(℉)
的关系?如果气温是摄氏32度,那相当于华氏多少度?二,解答题摄氏32度,那相当于华氏89.6度例已知两条直线y=2x-3和y=5-x.
(1)在同一坐标系内作出它们的图象;
(2)求出它们的交点A坐标;
(3)求出这两条直线与x轴围成的三角形ABC的面积;例 k为何值时,直线2k+1=5x+4y与k=2x+3y的交点在每四象限5。直线 分别交x 轴、y 轴于A、B两点,O是原点.
(1)求△AOB的面积;
(2)过△AOB的顶点能不能画出直线把△AOB分成面
积相等的两部分?如能,可以画出几条?
写出这样的直线所对应的函数关系式.AB即在△AOB 中,OA=3,OB=2.所以△AOB的面积: (3×2) ÷2=3O(2)能.可以画出3条,它别是:中点解: 该函数的图象如图(1)直线分别交x 轴、y 轴于A(3,0)、
B(0,-2)两点,二综合题M 例:随着数学手段不断更新,要求计算器进入课堂,某电子厂家经过市场调查,发现某种计算器的供应量x1(万个)与价格y1(万元)之间的关系,如图中供应线所示,而需求量x2(万个)与价格y2(万元)之间的关系,如图中需求线所示,如果你是这个电子厂的厂长,应计划生产这种计算器多少个,每个售价多少元,才能使市场达到供需平衡?6.一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前
每千克的土豆价格是多少?
(4)降价后他按每千克0.4元
将剩余土豆售完,这时他手中
的钱(含备用零钱)是26元,
试问他一共带了多少千克土豆?
(1)k、b的符号对图象的影响是怎样的?
(2)如何求一次函数的图象与坐标轴的交点坐标?
(3)如何画一次函数的图象?
(4)若两条直线互相平行,k的值是否会相同?
(5)会用待定系数法求一次函数的解析式吗?
(6)一次函数的性质如何表述?回顾与思考2.反比例函数 (k≠0) (1)k的符号对图象的影响是怎样的? (2)如何画反比例函数的图象?画图象时与上述
的一次函数的图象的画法有何区别?(3)双曲线经过一点,能确定它的解析式吗? (4)反比例函数的性质是如何描述的?位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限 y随x的增大而减小二四象限二四象限 y随x的增大而减小 y随x的增大而增大
填表分析正比例函数和反比例函数的区别例1 反比例函数的图象经过点A(2,3).
求这个函数的关系式.
请判断点B(1,6)是否在这个反比例函数的图象上.并说明理由.分析求函数的关系式,一般先设出关系式,再用待定系数法求出未
知数k.由题意知反比例函数的图象经过点A(2,3),也就是说点
A(2,3)在图象上,因此它的坐标满足函数的关系式,即当x=2时,
y=3,反过来也是如此,即一个点的坐标如果满足函数的关系式,
就是说这点在图象上.或者说函数的图象经过这个点.解: ①设 由题意有 , 则k=6,
所以这个函数的关系式为②点B(1,6)是否在这个反比例函数的图象上.因为当x=1时,
所以B(1,6)在这个反比例函数的图象上.
例题
讲解 例2 .气温随高度的升高而下降.下降的一般规律是从地面到高空11km
高处,每升高1km,气温下降6℃;高于11km时,气温几乎不再
变化.设某处地面气温20℃,该处高空x km处气温为y℃. .
(1)当0≤x≤11时,求y关于x的函数关系式 . .
(2)画出该处气温随高度(包括高于11km)而变化的图象;
(3)试分别求出该处在离地面4.5km及13km的高空处的气温.解: (1)当0≤x≤11时, y=20-6x(2) 该函数图象如图(3) 当 x=4.5时,
y=20-6×4.5=-7.离地面4.5km处的气温约为-7°.当在离地面13km的高空处时,
气温几乎不再变化,这时的气温
约为-46°.xyx 1. 如果点A(-3,a)与点B(3,4)关于y轴对称,
那么a的值为( )
A.3 B.-3 C.4 D.-4一 选择题AC3。 某厂今年前五个月生产某种产品的月产量Q(件)关于时间
t (月)的函数图象如图所示,则对这种产品来说,下列说法正确
的是( ).
A。1月至3月每月产量逐月增加,
4、5两月每月产量逐月减少
B. 1月至3月每月产量逐月增加,
4、5两月每月产量与3月持平
C. 1月至3月每月产量逐月增加,
4、5两个月停止生产
D. 1月至3月每月产量不变,
4、5两月停止生产B4.如图,温度计上表示了摄氏温度(℃)与华氏温度(℉)的刻度.
能否用一个函数关系式来表示摄氏温度y(℃)和华氏温度x(℉)
的关系?如果气温是摄氏32度,那相当于华氏多少度?二,解答题摄氏32度,那相当于华氏89.6度例已知两条直线y=2x-3和y=5-x.
(1)在同一坐标系内作出它们的图象;
(2)求出它们的交点A坐标;
(3)求出这两条直线与x轴围成的三角形ABC的面积;例 k为何值时,直线2k+1=5x+4y与k=2x+3y的交点在每四象限5。直线 分别交x 轴、y 轴于A、B两点,O是原点.
(1)求△AOB的面积;
(2)过△AOB的顶点能不能画出直线把△AOB分成面
积相等的两部分?如能,可以画出几条?
写出这样的直线所对应的函数关系式.AB即在△AOB 中,OA=3,OB=2.所以△AOB的面积: (3×2) ÷2=3O(2)能.可以画出3条,它别是:中点解: 该函数的图象如图(1)直线分别交x 轴、y 轴于A(3,0)、
B(0,-2)两点,二综合题M 例:随着数学手段不断更新,要求计算器进入课堂,某电子厂家经过市场调查,发现某种计算器的供应量x1(万个)与价格y1(万元)之间的关系,如图中供应线所示,而需求量x2(万个)与价格y2(万元)之间的关系,如图中需求线所示,如果你是这个电子厂的厂长,应计划生产这种计算器多少个,每个售价多少元,才能使市场达到供需平衡?6.一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前
每千克的土豆价格是多少?
(4)降价后他按每千克0.4元
将剩余土豆售完,这时他手中
的钱(含备用零钱)是26元,
试问他一共带了多少千克土豆?
