单项式乘以多项式[上学期]
图片预览









文档简介
课件39张PPT。13.2单项式与多项式相乘 单项式乘以多项式m(a+b+c)复习回顾:1、同底数幂的乘法:2、幂的乘方:3、积的乘方:am.an=am+n (m,n均为整数)(am)n=amn (m,n均为正整数)(ab)n=an.bn (n为正整数)1、单项式与单项式相乘的法则? 2、完成下列各题: ①2x2·(-4xy)=
②(-2x2)·(-3xy)=
③(-9a2 b3)·(8ab2) =
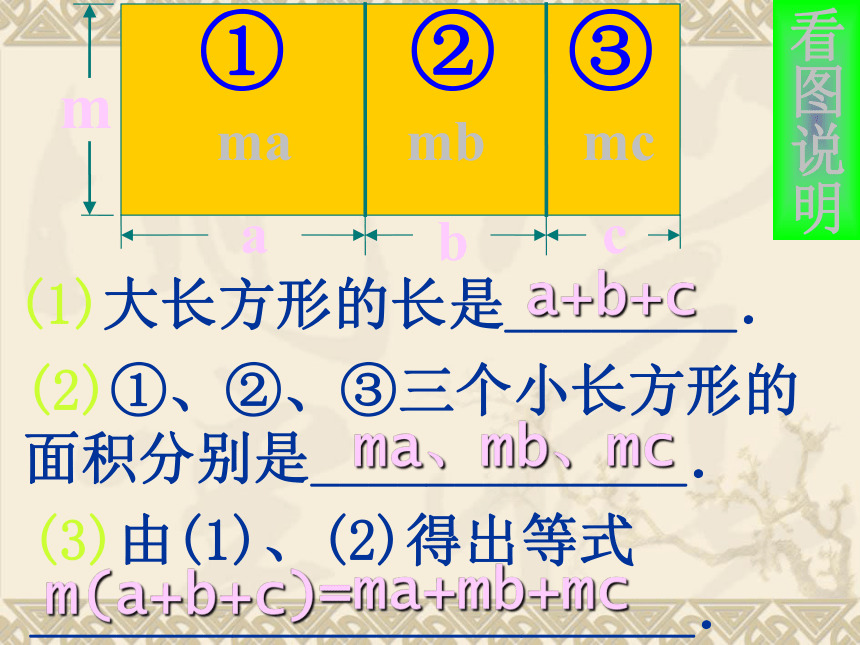
④12×( - + )=-8x3y6x3y-72a3 b59 单项式与单项式相乘,只要将它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式.单×单=(系数×系数)(同底数幂×同底数幂)(单独的幂). 单项式与单项式相乘: 知识回顾口答计算结果: 12×( - + )= 你是怎么算的? 12×( - + ) =12 × - 12 × + 12 ×=8-9 + 10 = 9 m(a+b+c)= am+bm+cm (1)大长方形的长是________.(2)①、②、③三个小长方形的 面积分别是_____________.(3)由(1)、(2)得出等式
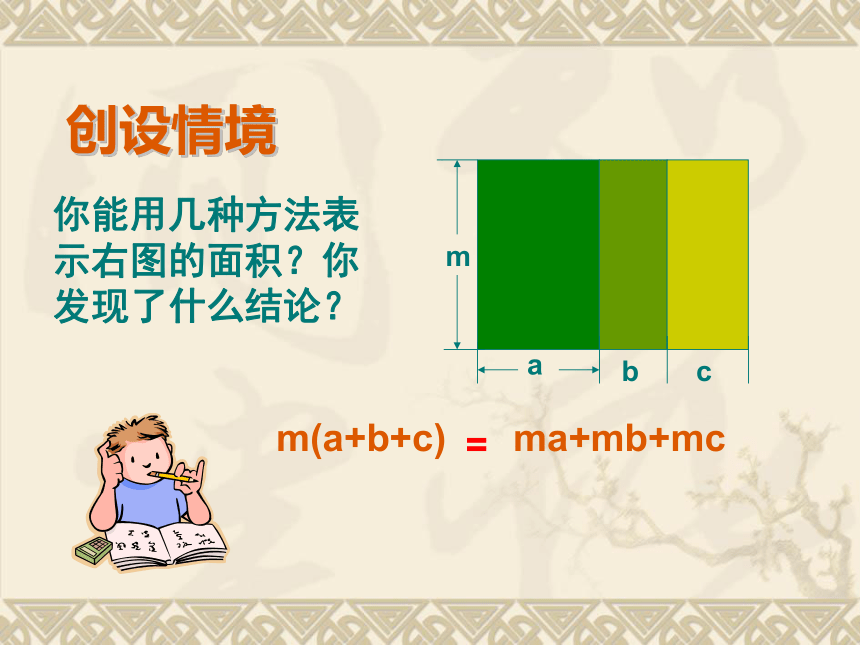
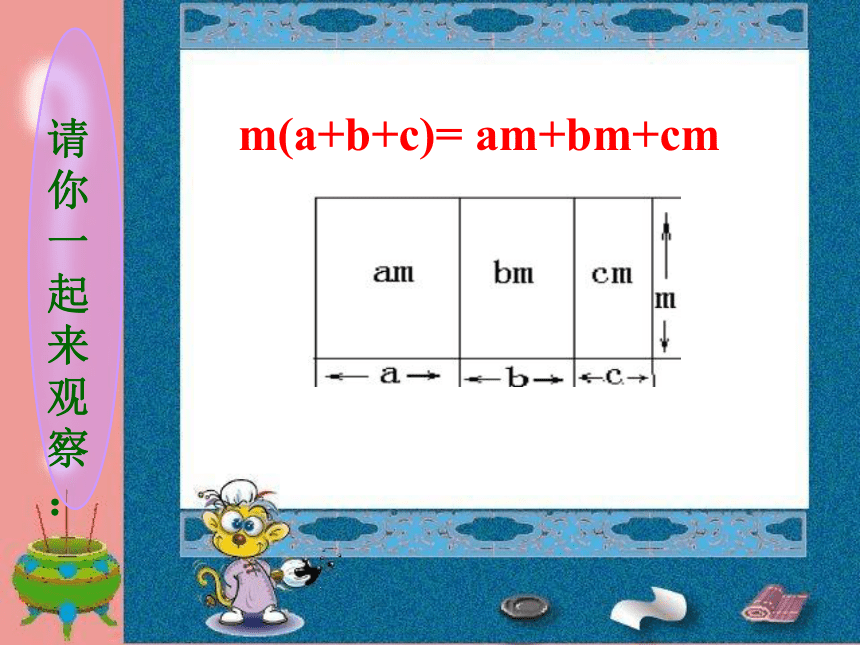
_______________________.①②③a+b+cma、mb、mcm(a+b+c)看图说明=ma+mb+mc创设情境mabc你能用几种方法表示右图的面积?你发现了什么结论?m(a+b+c)ma+mb+mc=新课导入当m=a时, +ab+aca·aa2当m=abc时,abc·a+abc·b+abc·c=a2bc+ab2c+abc2法则:单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加。m(a+b+c)= am+bm+cm a·(3a+b)平方米 1).来我们学校的路上看到有一块三角形的路标牌,其一边长(3a+b)米,这条边上的高为2a 米,大家来算一下这块路牌的面积有多少?[列式]2).老师手中的玻璃杯,其底面直径为2a㎝,高为(2b+4) ㎝,请你帮老师算一下这只杯子的体积有多少?[列式]πa2·(2b+4) cm3 =你能用所学的知识解释这个等式吗 ?m(a+b+c)=mambmc++2a2(3a2-5b)=2a2.3a22a2.(-5b)+=6a4-10a2b(-2a2)(3ab2-5b)=(-2a2).3ab2(-2a2).(-5b)+=-6a3b2+10a2b类似的:单项式与多项式相乘乘法分配律单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.单项式与多项式相乘的法则:例1. 计算: (-2a2) ·(3ab2-5ab3) 法则:单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加。 a·(3a+b) πa2·(2b+4) =3a2+ ab=2πa2b+4πa2 m(a+b+c)= am+bm+cm = -a3b- 2a2 b2 -5 a3b+ 5a2 b2 解:原式=(-2a2 ) · + (-2a2 ) · b2例2.计算:-2a2( +b2 ) -5a(a2b-ab2) = -6a3b+ 3a2 b2 +(-5a) · a2b+ (-5a) ·(- ab2) 法则:单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加。 例1 计算
(1)(-4x)·(2x2+3x-1) ( ab2-2ab)· ab (2)练习反馈1、3a(5a-2b) 2、(x-3y)(-6x) 做一做⑴、⑵、2、化简:1、计算: ⑴ ﹙ x-3y ﹚·﹙-6x﹚
⑵5x﹙2x2-3x+4﹚练一练 x(x2+3)-3x(x2-x+1) 做一做〖-2x3+3x2〗1.计算:
(1)?3x3y ? (2xy2-3xy);
(2) 2x ?(3x2-xy+y2);
(3) -3a ?(2a2-a+4).?2.先化简,再求值。?(x=-2)
x(x2-10)+3x2(x+2)-2x(3x-5) 练习:1、计算
(1)3a(5a-2b) (2)(x-3y)(-6x)
2、化简:x(x-1)+2x(x+1)-3x(2x-5)答案:1、(1)15a2-6ab (2)-6x2+18yx
2、-3x2+16x??2.先化简,再求值?(x= -2) x(x2-10)+3x2(x+2)-2x(3x-5) 解:原式 ==4x3当x= -2时,原式=4x3=4×(-2)3 =4×(-8) = -32x3–10x+3x3+6 x2–6 x2+10x 1.当多项式中的项数多于三项时,法则是否成立?2 .非零单项式乘以不含同类项的多项式,其积仍是多项式,积的项数与多项式的项数有什么关系?2、解方程:x(x+1)=x2 +33、解不等式:x2+9>x(x-3)解: x2 + x=x2 +3x=3解:x2+9> x2 -3 x3 x > - 9 x > - 3 1、计算:2 an-1(an+1-3a) 解:原式=2an-1· an+1 + 2an-1·(-3a) =2a 2n - 6an 2)已知x+2y=0,
试求x3+2xy(x+y)+4 y3的值1)小斌同学说当n为正整数时, n(4n+1)-4n(n-2)的值是9的倍数,你认为他说的有道理吗? 提示:原式= x3+2x2 y+2xy2+4 y3 = x2 (x+2y)+2y2 (x+2y)解:2x·4y?小明家新买房子结构如图,父母打算把卧室以外的部分地面铺上地砖,请你帮他们算一下,至少需要购买多少地砖?如果某种地砖价格是a元/㎡,那么购买所需地砖至少要多少元钱?(图中单位为m)至少需要钱:9axy元=9xy+x(4y-2y)+y(4x-3x)1)注意不要漏乘任何一项。 同学们,通过这节课,你觉得单项式与多项式相乘要注意什么呀?2)注意“-”的问题。 3)在几个单项式乘以多项式的混合运算中,要注意运算顺序,完成乘法后,要合并同类项,得出最简结果。 4)逆用单项式与多项式相乘的法则,有时可以简化解题过程。 回顾交流:本节课我们学习了那些内容?单项式乘以多项式的依据是什么?如何进行单项式与多项式乘法运算?小 结1、注意不要漏乘任何一项。
2、注意“-”的问题。
3、在几个单项式乘以多项的混合运算中,要注意运算顺序,完成乘法后,要合并同类项,得出最简结果。小结1、单项式与多项式相乘的依据是乘法对加法的分配律
2、单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数相同,注意不要漏乘项
3、积的每一项的符号由原多项式各项符号和单项式的符号来决定几点注意:1.单项式乘多项式的结果是多项式,
积的项数与原多项式的项数相同。 3.不要出现漏乘现象,运算要有顺序。2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:
同号相乘得正,异号相乘得负 ?我们的新校园内计划砌一个形状如图甲所示的喷水池,后有人建议改为图乙所示的形状,且外圆直径不变,只是担心原来准备好的材料不够用,请你通过计算,比较一下哪一种方案需要用的材料多(即哪个周长更长)?再 见!Thank you!作 业1、P28 3、4
2、预习:多项式乘以多项式业精于勤荒于嬉1.单项式与多项式相乘,就是用单项式去乘
多项式的________,再把所得的积________二.填空2.4(a-b+1)=___________________每一项相加4a-4b+43.3x(2x-y2)=___________________6x2-3xy24.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz5.(-2a2)2(-a-2b+c)=___________________-4a5-8a4b+4a4c三.选择下列计算错误的是( )
(A)5x(2x2-y)=10x3-5xy
(B)-3xa+b ?4xa-b=-12x2a
(C)2a2b?4ab2=8a3b3
(D)(-xn-1y2)?(-xym)2=xnym+2 D=(-xn-1y2)?(x2y2m)=-xn+1y2m+2谢谢指导谢谢在寻求真理的长征中,唯有学习,不断地学习,勤奋地学习,有创造地学习,才能越重山,跨峻岭。
——华罗庚
②(-2x2)·(-3xy)=
③(-9a2 b3)·(8ab2) =
④12×( - + )=-8x3y6x3y-72a3 b59 单项式与单项式相乘,只要将它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式.单×单=(系数×系数)(同底数幂×同底数幂)(单独的幂). 单项式与单项式相乘: 知识回顾口答计算结果: 12×( - + )= 你是怎么算的? 12×( - + ) =12 × - 12 × + 12 ×=8-9 + 10 = 9 m(a+b+c)= am+bm+cm (1)大长方形的长是________.(2)①、②、③三个小长方形的 面积分别是_____________.(3)由(1)、(2)得出等式
_______________________.①②③a+b+cma、mb、mcm(a+b+c)看图说明=ma+mb+mc创设情境mabc你能用几种方法表示右图的面积?你发现了什么结论?m(a+b+c)ma+mb+mc=新课导入当m=a时, +ab+aca·aa2当m=abc时,abc·a+abc·b+abc·c=a2bc+ab2c+abc2法则:单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加。m(a+b+c)= am+bm+cm a·(3a+b)平方米 1).来我们学校的路上看到有一块三角形的路标牌,其一边长(3a+b)米,这条边上的高为2a 米,大家来算一下这块路牌的面积有多少?[列式]2).老师手中的玻璃杯,其底面直径为2a㎝,高为(2b+4) ㎝,请你帮老师算一下这只杯子的体积有多少?[列式]πa2·(2b+4) cm3 =你能用所学的知识解释这个等式吗 ?m(a+b+c)=mambmc++2a2(3a2-5b)=2a2.3a22a2.(-5b)+=6a4-10a2b(-2a2)(3ab2-5b)=(-2a2).3ab2(-2a2).(-5b)+=-6a3b2+10a2b类似的:单项式与多项式相乘乘法分配律单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.单项式与多项式相乘的法则:例1. 计算: (-2a2) ·(3ab2-5ab3) 法则:单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加。 a·(3a+b) πa2·(2b+4) =3a2+ ab=2πa2b+4πa2 m(a+b+c)= am+bm+cm = -a3b- 2a2 b2 -5 a3b+ 5a2 b2 解:原式=(-2a2 ) · + (-2a2 ) · b2例2.计算:-2a2( +b2 ) -5a(a2b-ab2) = -6a3b+ 3a2 b2 +(-5a) · a2b+ (-5a) ·(- ab2) 法则:单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加。 例1 计算
(1)(-4x)·(2x2+3x-1) ( ab2-2ab)· ab (2)练习反馈1、3a(5a-2b) 2、(x-3y)(-6x) 做一做⑴、⑵、2、化简:1、计算: ⑴ ﹙ x-3y ﹚·﹙-6x﹚
⑵5x﹙2x2-3x+4﹚练一练 x(x2+3)-3x(x2-x+1) 做一做〖-2x3+3x2〗1.计算:
(1)?3x3y ? (2xy2-3xy);
(2) 2x ?(3x2-xy+y2);
(3) -3a ?(2a2-a+4).?2.先化简,再求值。?(x=-2)
x(x2-10)+3x2(x+2)-2x(3x-5) 练习:1、计算
(1)3a(5a-2b) (2)(x-3y)(-6x)
2、化简:x(x-1)+2x(x+1)-3x(2x-5)答案:1、(1)15a2-6ab (2)-6x2+18yx
2、-3x2+16x??2.先化简,再求值?(x= -2) x(x2-10)+3x2(x+2)-2x(3x-5) 解:原式 ==4x3当x= -2时,原式=4x3=4×(-2)3 =4×(-8) = -32x3–10x+3x3+6 x2–6 x2+10x 1.当多项式中的项数多于三项时,法则是否成立?2 .非零单项式乘以不含同类项的多项式,其积仍是多项式,积的项数与多项式的项数有什么关系?2、解方程:x(x+1)=x2 +33、解不等式:x2+9>x(x-3)解: x2 + x=x2 +3x=3解:x2+9> x2 -3 x3 x > - 9 x > - 3 1、计算:2 an-1(an+1-3a) 解:原式=2an-1· an+1 + 2an-1·(-3a) =2a 2n - 6an 2)已知x+2y=0,
试求x3+2xy(x+y)+4 y3的值1)小斌同学说当n为正整数时, n(4n+1)-4n(n-2)的值是9的倍数,你认为他说的有道理吗? 提示:原式= x3+2x2 y+2xy2+4 y3 = x2 (x+2y)+2y2 (x+2y)解:2x·4y?小明家新买房子结构如图,父母打算把卧室以外的部分地面铺上地砖,请你帮他们算一下,至少需要购买多少地砖?如果某种地砖价格是a元/㎡,那么购买所需地砖至少要多少元钱?(图中单位为m)至少需要钱:9axy元=9xy+x(4y-2y)+y(4x-3x)1)注意不要漏乘任何一项。 同学们,通过这节课,你觉得单项式与多项式相乘要注意什么呀?2)注意“-”的问题。 3)在几个单项式乘以多项式的混合运算中,要注意运算顺序,完成乘法后,要合并同类项,得出最简结果。 4)逆用单项式与多项式相乘的法则,有时可以简化解题过程。 回顾交流:本节课我们学习了那些内容?单项式乘以多项式的依据是什么?如何进行单项式与多项式乘法运算?小 结1、注意不要漏乘任何一项。
2、注意“-”的问题。
3、在几个单项式乘以多项的混合运算中,要注意运算顺序,完成乘法后,要合并同类项,得出最简结果。小结1、单项式与多项式相乘的依据是乘法对加法的分配律
2、单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数相同,注意不要漏乘项
3、积的每一项的符号由原多项式各项符号和单项式的符号来决定几点注意:1.单项式乘多项式的结果是多项式,
积的项数与原多项式的项数相同。 3.不要出现漏乘现象,运算要有顺序。2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:
同号相乘得正,异号相乘得负 ?我们的新校园内计划砌一个形状如图甲所示的喷水池,后有人建议改为图乙所示的形状,且外圆直径不变,只是担心原来准备好的材料不够用,请你通过计算,比较一下哪一种方案需要用的材料多(即哪个周长更长)?再 见!Thank you!作 业1、P28 3、4
2、预习:多项式乘以多项式业精于勤荒于嬉1.单项式与多项式相乘,就是用单项式去乘
多项式的________,再把所得的积________二.填空2.4(a-b+1)=___________________每一项相加4a-4b+43.3x(2x-y2)=___________________6x2-3xy24.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz5.(-2a2)2(-a-2b+c)=___________________-4a5-8a4b+4a4c三.选择下列计算错误的是( )
(A)5x(2x2-y)=10x3-5xy
(B)-3xa+b ?4xa-b=-12x2a
(C)2a2b?4ab2=8a3b3
(D)(-xn-1y2)?(-xym)2=xnym+2 D=(-xn-1y2)?(x2y2m)=-xn+1y2m+2谢谢指导谢谢在寻求真理的长征中,唯有学习,不断地学习,勤奋地学习,有创造地学习,才能越重山,跨峻岭。
——华罗庚
